2020九年级数学下册 第1章 解直角三角形 1

2020九年级数学下册 第1章 解直角三角形 1

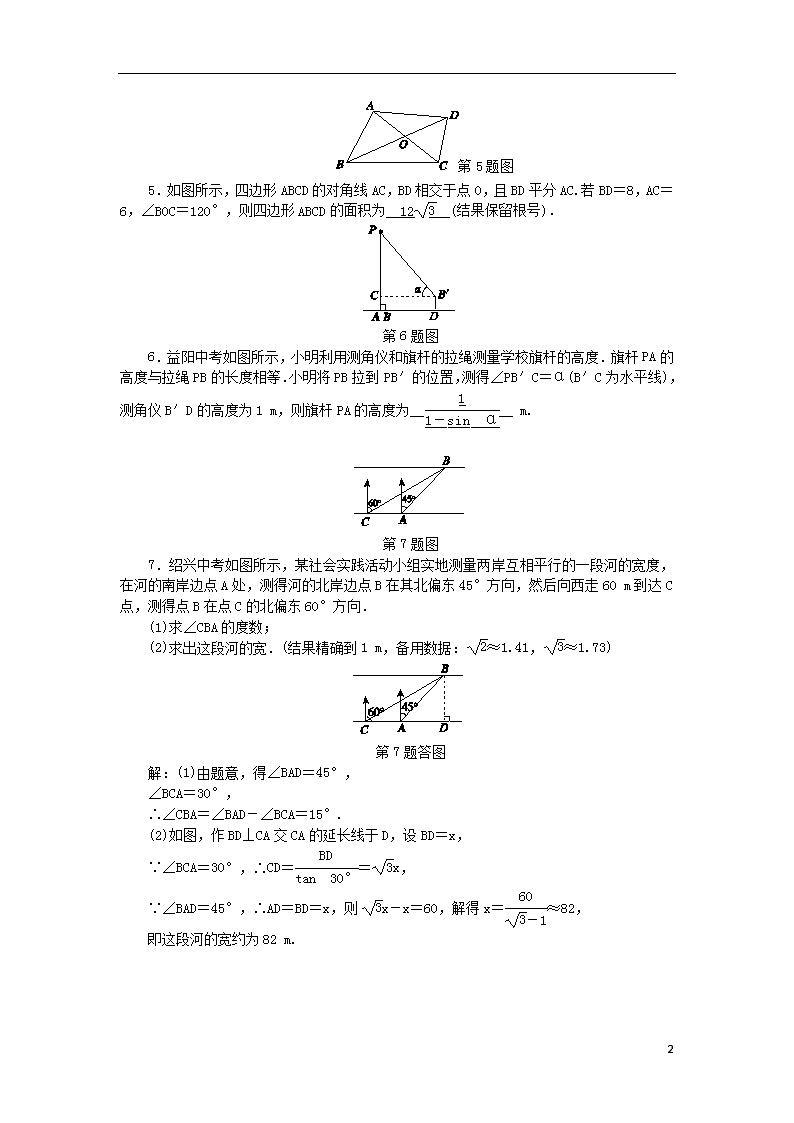
1.3 解直角三角形(3)‎ ‎(见A本57页)‎ A　练就好基础　基础达标 ‎1．王英同学从A地沿北偏西60°方向走‎100 m到B地，再从B地向正南方向走‎200 m到C地，此时王英同学离A地(　D　)‎ A．‎150 m B．‎50‎m C．‎100 m D．‎100‎m ‎2．如图所示，要测量B点到河岸AD的距离，在A点测得∠BAD＝30°，在C点测得∠BCD＝60°，又测得AC＝‎100 m，则B点到河岸AD的距离为(　B　)‎ A．‎100 m B．‎50 m C. m D．‎‎50 m ‎　第2题图 ‎　　　　第3题图 ‎3．苏州中考如图所示，长‎4 m的楼梯AB的倾斜角∠ABD为60°.为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为(　B　)‎ A．‎2 m B．‎2 m C．(2－2) m D．(2－2) m ‎4．西宁中考如图所示，为保护门源百里油菜花海，由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB，AC. 若∠B＝56°，∠C＝45°，则游客中心A到观景长廊BC的距离AD的长约为__60__ m．(sin 56°≈0.8，tan 56°≈1.5)‎ 第4题图 6‎ ‎　　第5题图 ‎5．如图所示，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC.若BD＝8，AC＝6，∠BOC＝120°，则四边形ABCD的面积为__12__(结果保留根号)．‎ 第6题图 ‎6．益阳中考如图所示，小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C＝α(B′C为水平线)，测角仪B′D的高度为‎1 m，则旗杆PA的高度为____ m.‎ 第7题图 ‎7．绍兴中考如图所示，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走‎60 m到达C点，测得点B在点C的北偏东60°方向．‎ ‎(1)求∠CBA的度数；‎ ‎(2)求出这段河的宽．(结果精确到‎1 m，备用数据：≈1.41，≈1.73)‎ 第7题答图 解：(1)由题意，得∠BAD＝45°，‎ ‎∠BCA＝30°，‎ ‎∴∠CBA＝∠BAD－∠BCA＝15°.‎ ‎(2)如图，作BD⊥CA交CA的延长线于D，设BD＝x，‎ ‎∵∠BCA＝30°，∴CD＝＝x，‎ ‎∵∠BAD＝45°，∴AD＝BD＝x，则x－x＝60，解得x＝≈82，‎ 即这段河的宽约为82 m.‎ 6‎ 第8题图 ‎8．2017·乌鲁木齐中考一艘渔船位于港口A北偏东60°方向，距离港口20海里的B处，它沿北偏西37°方向航行至C处突然出现故障，在C处等待救援，B，C之间的距离为10海里，救援船从港口A出发20分钟到达C处，求救援艇的航行速度．(sin 37°≈0.6，cos 37°≈0.8，≈1.732，结果取整数)‎ 第8题答图 解：作辅助线如图所示：‎ BD⊥AD，BE⊥CE，CF⊥AF，‎ 由题意知，∠FAB＝60°，∠CBE＝37°，‎ ‎∴∠BAD＝30°，‎ ‎∵AB＝20海里，‎ ‎∴BD＝10海里，‎ 在Rt△ABD中，AD＝＝10≈17.32(海里)，‎ 在Rt△BCE中，sin37°＝，‎ ‎∴CE＝BC·sin37°≈0.6×10＝6(海里)，‎ ‎∵cos37°＝，∴EB＝BC·cos37°≈0.8×10＝8(海里)，‎ EF＝AD＝17.32海里，∴FC＝EF－CE＝11.32(海里)，‎ AF＝ED＝EB＋BD＝18(海里)，‎ 在Rt△AFC中，‎ AC＝＝≈21.26(海里)，‎ ‎21．26÷＝64(海里/小时)．‎ 答：救援艇的航行速度大约是64海里/小时．‎ B　更上一层楼　能力提升 ‎9．扬州中考若锐角△ABC内接于⊙O，点D在⊙O外(与点C在AB同侧)，有下列三个结论：①sin∠C>sin∠D；②cos∠C>cos∠D；③tan∠C>tan∠D.正确的结论为(　D　)‎ A．①② B．②③ C．①②③ D．①③‎ 6‎ 第10题图 ‎10．如图所示，一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以‎28 km/h的速度向正东方向航行，半小时后到达B处，在B处看见灯塔M在北偏东15°方向，此时，灯塔M与渔船的距离是(　A　)‎ A．‎7 km B．‎14 km C．‎7 km D．‎‎14 km 第11题图 ‎11．2017·苏州中考如图所示，在一笔直的沿湖道路l上有A，B两个游船码头，观光岛屿C在码头Α北偏东60°的方向，在码头B北偏西45°的方向，AC＝‎4 km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B.设开往码头A，B的游船速度分别为v1，v2，若回到A，B所用时间相等，则＝____(结果保留根号)．‎ C　开拓新思路　拓展创新 ‎12．如图所示，在平面直角坐标系中，△ABC是⊙O的内接三角形，AB＝AC，点P是的中点，连结PA，PB，PC.‎ ‎(1)如图(a)，若∠BPC＝60°，求证：AC＝AP；‎ ‎(2)如图(b)，若sin∠BPC＝，求tan∠PAB的值．‎ 图(a)　　　　　图(b)‎ 第12题图 解：(1)证明：∵∠BAC＝∠BPC＝60°.‎ 又∵AB＝AC，∴△ABC为等边三角形，‎ ‎∴∠ACB＝60°，∵点P是的中点，∴∠ACP＝30°，‎ 又∵∠APC＝∠ABC＝60°，∴AC＝AP.‎ 6‎ 第12题答图 ‎(2)如图，连结AO并延长交PC于点E，交BC于点F，过点E作EG⊥AC于点G，连结OC.‎ ‎∵AB＝AC，∴AF⊥BC，BF＝CF.‎ 又∵点P是的中点，∴∠ACP＝∠PCB，‎ ‎∴EG＝EF.‎ ‎∵∠BPC＝∠BAC，又∵∠BAC＝∠FOC，‎ ‎∴∠BPC＝∠FOC，‎ ‎∴sin∠FOC＝sin∠BPC＝.‎ 设FC＝24a，则OC＝OA＝25a，‎ ‎∴OF＝7a，AF＝32a.‎ 在Rt△AFC中，AC2＝AF2＋FC2，∴AC＝40a.‎ 在Rt△AGE和Rt△AFC中，sin∠FAC＝＝，‎ ‎∴＝，∴EG＝12a.‎ ‎∴tan∠PAB＝tan∠PCB＝＝＝. ‎ ‎13．如图所示的晾衣架，支架主视图的基本图形是菱形，其示意图如图(b)所示．晾衣架伸缩时，点G在射线DP上滑动，∠CED的大小也随之发生变化．已知每个菱形边长均等于‎20 cm，且AH＝DE＝EG＝‎20 cm.‎ ‎(1)当∠CED＝60°时，求C，D两点间的距离；‎ ‎(2)当∠CED由60°变为120°时，点A向左移动了多少 cm？(结果精确到‎0.1 cm)‎ ‎(3)设DG＝x，当∠CED的变化范围为60°～ 120°(包括端点值)时，求x的取值范围．(结果精确到‎0.1 cm，参考数据：≈1.732)‎ ‎　　　　　　图(a)　　　　　　　　　　图(b)‎ 第13题图 解：(1)如图(a)，连结CD，‎ 第13题答图(a)‎ 6‎ ‎　　第13题答图(b)‎ ‎∵每个菱形的边长都是20 cm, 且DE＝20 cm，‎ ‎∴CE＝DE，‎ ‎∵∠CED＝60°，∴△CED是等边三角形，‎ ‎∴CD＝20 cm, ∴C，D两点之间的距离是20 cm.‎ ‎(2)如图(b)，‎ 作EM⊥CD于点M, 在△CED中，CE＝DE, ∠CED＝120°，‎ ‎∴∠ECD＝30°，∴EM＝CE＝10 cm，‎ ‎∴CM＝10 cm，∴CD＝20 cm，‎ ‎∴点C向左移动了(20－20) cm，‎ ‎∴点A向左移动了(20－20)×3≈43.9(cm)．‎ ‎(3)如图(a)，当∠CED＝60°时， ∵ED＝EG, ∠CGD＝30°，‎ 在Rt△CGD中，cos 30°＝，∵CG＝40 cm，‎ ‎∴DG＝20≈34.6(cm)．‎ 如答图(b)，当∠CED＝120°时， ∠CGD＝60°，‎ ‎∴DG＝CG＝20 cm，∴20 cm≤x≤34.6 cm.‎ 6‎