- 2021-06-18 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
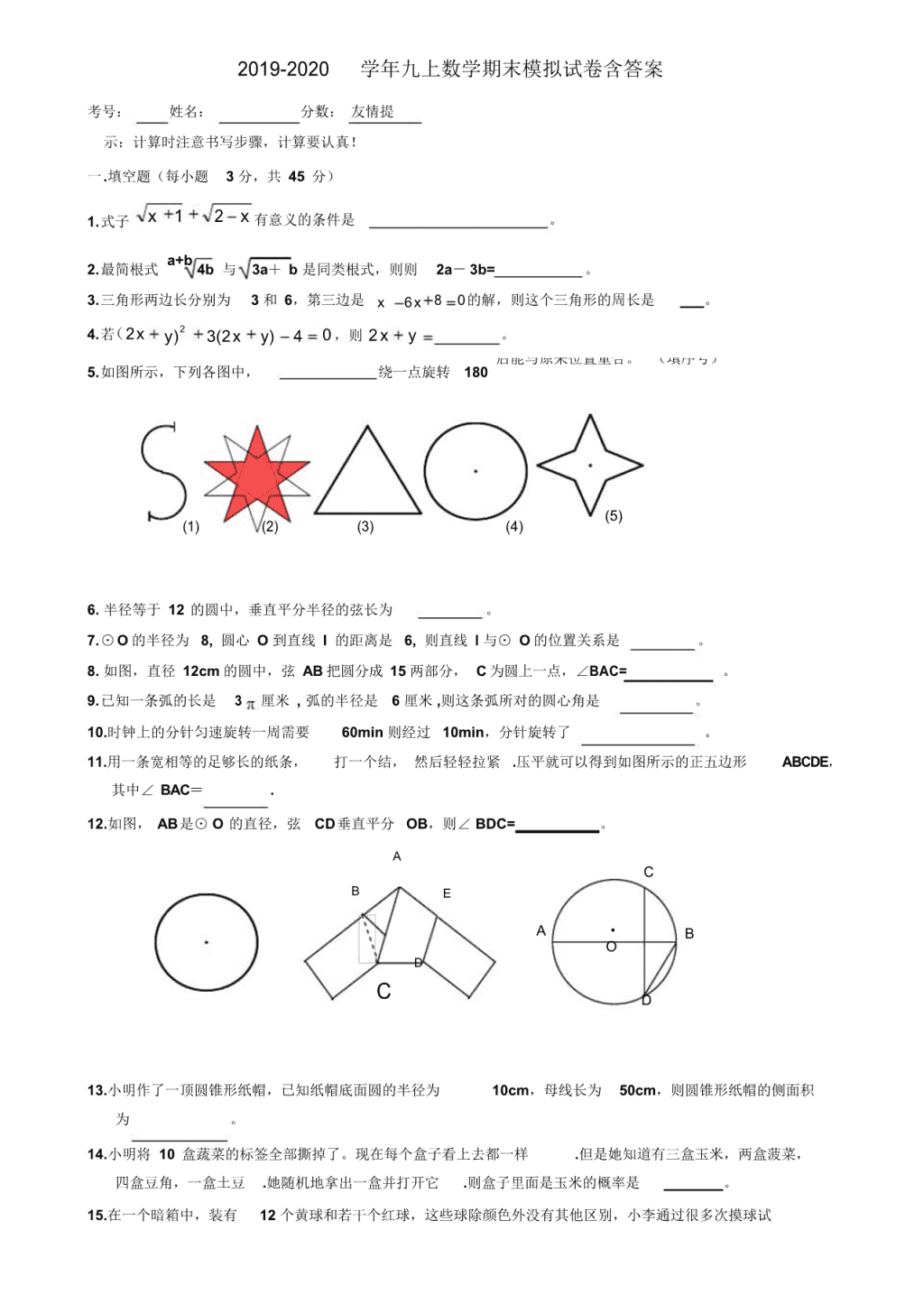
【40套试卷合集】重庆市江津实验中学2019-2020学年数学九上期末模拟试卷含答案
2 2019-2020 学年九上数学期末模拟试卷含答案 考号: 姓名: 分数: 友情提 示:计算时注意书写步骤,计算要认真! 一.填空题(每小题 3 分,共 45 分) 1.式子 x 1 2 x 有意义的条件是 。 2.最简根式 a+b 4b 与 3a+ b 是同类根式,则则 2a- 3b= 。 3.三角形两边长分别为 3 和 6,第三边是 x 6x 8 0的解,则这个三角形的周长是 。 4.若(2x y)2 3(2x y) 4 0 ,则 2x y 。 0后能与原来位置重合。 (填序号) 5.如图所示,下列各图中, 绕一点旋转 180 (1) (2) (3) (4) (5) 6. 半径等于 12 的圆中,垂直平分半径的弦长为 。 7.⊙O 的半径为 8, 圆心 O 到直线 l 的距离是 6, 则直线 l 与⊙ O 的位置关系是 。 8. 如图,直径 12cm 的圆中,弦 AB 把圆分成 15 两部分, C 为圆上一点,∠BAC= 。 9.已知一条弧的长是 3 厘米 , 弧的半径是 6 厘米 ,则这条弧所对的圆心角是 。 10.时钟上的分针匀速旋转一周需要 60min 则经过 10min,分针旋转了 。 11.用一条宽相等的足够长的纸条, 打一个结, 然后轻轻拉紧 .压平就可以得到如图所示的正五边形 ABCDE, 其中∠ BAC= . 12.如图, AB是⊙ O 的直径,弦 CD垂直平分 OB,则∠ BDC= 。 A C B E A · B O D C D 13.小明作了一顶圆锥形纸帽,已知纸帽底面圆的半径为 10cm,母线长为 50cm,则圆锥形纸帽的侧面积 为 。 14.小明将 10 盒蔬菜的标签全部撕掉了。现在每个盒子看上去都一样 .但是她知道有三盒玉米,两盒菠菜, 四盒豆角,一盒土豆 .她随机地拿出一盒并打开它 .则盒子里面是玉米的概率是 。 15.在一个暗箱中,装有 12 个黄球和若干个红球,这些球除颜色外没有其他区别,小李通过很多次摸球试 2 2 2 2 验 后 , 发 现 从 中 随 机 摸 出 一 个 红 球 的 频 率 值 稳 定 在 25%, 则 该 袋 中 红 球 的 个 数 有 可 能 是 个. 二.选择题(每小题 3 分,共 15 分) 1.下列等式一定成立的是 ( ) A. 9 16 9 16 B. a b a b C. 4 4 D. (a b) a b 1 2.化简 2 1 2 的结果为 ( ) 3 1 A. 3 2 B. 3 2 C. 2 2 3 D. 3 2 2 3.下面是李刚同学在一次测验中解答的填空题,其中答对的是 ( ) 2 A.若 x =4,则 x= 2 B.方程 x(2x-1)= 2x-1 的解为 x=1 2 C.若 x +2x+k=0的一个根为 1,则 k= 3 D.若分式 x -3x+2 的值为零,则 x=1, 2 x-1 4.下列图形中,既是轴对称图形又是中心对称图形的是 ( ) 5.如图, 8× 8 方格纸上的两条对称轴 EF、 MN 相交于中心点 O,对△ ABC 分别作下列变换: ①先以点 A 为中心顺时针方向旋转 90°,再向右平移 4 格、向上平移 4 格; ②先以点 O 为中心作中心对称图形,再以点 A 的对应点为中心逆时针方向旋转 90°; ③先以直线 MN 为轴作轴对称图形,再向上平移 4 格,再以点 A 的对应点为中心顺时针方向旋转 90°。 其中,能将△ ABC 变换成△ PQR 的是 ( ) A.①② B.①③ C.②③ D.①②③ N Q P R E F O A B C M 三.解答题(本大题共 8 小题,满分 60 分.解答应写出文字说明 .证明过程或演算步骤) 1.计算 2 12 3 48 4 1 8 3 27 (4 分) 2. 解方程 5x 2 7x 2 0 (4 分) 3.某商场设立了一个可以自由转动的转盘 ,并规定:顾客购物 10 元以上就能获得一次转动转盘的机会 ,当转 盘停止时 ,指针落在哪一区域就可以获得相应的奖品 .下表是活动进行中的一组统计数据: (1) 计算并完成表格: (2 分) 转动转盘的次数 n 100 150 200 500 800 1000 落在“铅笔”的次数 m 68 111 136 345 564 701 落在“铅笔”的频率 m 0.68 0.74 0.69 0.71 n (2). 请估计 ,当 n 很大时 ,频率将会接近多少? (1 分) (3). 假如你去转动该转盘一次 ,你获得铅笔的概率约是多少? (1 分) (4). 在该转盘中 ,表示“铅笔”区域的扇形的圆心角约是多少 (精确到 1° ) ( 2 分) 铅笔 可乐 30 % 4. 如图,画出△ ABC 关于原点 O 对称的△ A1B1C1,并求出点 A1, B1,C1 的坐标。 (6 分) y A (-3,2) 3 C (2,3) 2 1 -3 -2 -1 O 1 2 3 x B (-2,-1) -1 -2 第 12 题 5.如图, ABCD 是围墙,一根 5 米长的绳子,一端拴在围墙一角的柱子上,另一端拴着一只羊, (1)请在 图中画出羊活动的区域。 (2)求出羊活动区域的面积。 (6 分) D 羊 C 0 120 5m 4m A B 围墙 6.如图,一面积是 150 平方米的长方形鸡场,鸡场的一边靠墙(墙长 18 米),墙对面有一个 2 米宽的门, 另三边用竹篱笆围城,篱笆总长 33 米,求:鸡场的长和宽各为多少米? (8 分) 7.如图, PA 切⊙ O 于 A,OP 交⊙ O 于 B,BP=2,AP=2 3 cm,求图中阴影部分的周长和面积 (结果保留 ). (10 分) 8.如图: AB 是⊙ O 的直径,以 OA 为直径的⊙ O1 与⊙ O 的弦 AC交于 D,DE⊥OC,垂足为 E。 (1).求证: AD=DC (5 分) (2) .求证: DE 是的切线 (5 分) (3) .如果 OE=EC,请判断四边形 O1OED 是什么四边形,并证明你的结论。 (6 分) 温馨提示:恭喜你已经解答完所有问题,请再仔细检查一次,预祝你取得好成绩! (5 2 2019-2020 学年九上数学期末模拟试卷含答案 考号: 姓名: 分数: 友情提 示:计算时注意书写步骤,计算要认真! 一.填空题(每小题 3 分,共 45 分) 1.写出一个无理数,并且使它与 3 2 的积是有理数 2.在一个不透明的盒子中装有 2 个白球, n 个黄球,它们除颜色不同外,其余均相同.若 从中随机摸出一个球,它是白球的概率为 2 , 则 n = 。 3 3.已知点 O 为△ ABC 的内心,∠ ABC=50°,∠ ACB=70 °,∠ BOC = 。 4.直线 y=x+3 上有一点 P(-5,m),则 P 点关于原点的对称点 P′坐标为 . 5.当 ab<0,化简 ab = . 6.某厂一月份生产机器 100 台,计划第.一.季.度. 共生产 380 台。设二 .三月份每月的平均增长率为 x,则根据 题意列出的方程是 。 7.直角三角形的两条直角边分别为 12 cm 和 5 cm,则其外接圆的半径为 cm . 8.已知圆锥的底面直径为 6cm,高为 4cm,则圆锥的全面积是 cm2 9.P 为⊙ O 内一点, OP=3,半径为 5,过 P 点的最短的弦长为 。 10.如图 , ⊙O 的直径 AB 11.如图,⊙ O 的半径 OC 8cm,C 为 ⊙O 上的一点 , ∠ ADC=30° ,则 AC= cm 10cm ,直线 l⊥CO,垂足为 H,交⊙ O 于 A、B 两点, AB 16cm,直线 l 平 移 厘米时能与⊙ O 相切。 12.如图,在△ ABC 中, BC=4,以点 A 为圆心, 2 为半径的⊙ A 与 BC相切于点 D,交 AB 于 E,交 AC于 F, 点 P 是⊙ A 上的一点,且∠ EPF=40°,则图中阴影部分的面积是 (结果保留 ) C A B O D 13.两圆的半径是方程 x 7x 12 0 两实数根,圆心距为 8,两圆的位置关系是 。 14.一个均匀的立方体骰子六个面上标有数 1, 2, 3, 4,5,6,若以连续掷两次骰子得到的数 m 和 n 作为 点 P 的坐标,则点 P 落在反比例函数 y 上的点)的概率是 。 15.观察下列各式: 6 图象与坐标轴所围成区域内(含落在此反比例函数的图象 x 1 1 1 1 1 11 2 , 2 3 , 3 4 ,.... 3 3 4 4 5 5 请你将发现的规律用含自然数 n(n≥ 1)的等式表示出 来 。 二.选择题(每小题 3 分,共 15 分) 2 16.用如下一种形状的地砖,不能把地面铺成无缝隙又不重叠的是 A.正三角形 B.正方形 C.长方形 D.正五边形 17.下面图形中既是轴对称图形又是中心对称图形的是 ( ( ) ) A.菱形 B.等边三角形 C.等腰梯形 D.两平行四边形 18.下列三个命题中正确的是 A.三点确定一个圆; B.垂直于弦的直径平分这条弦; ( ) C.相等圆心角所对的弧相等; D.圆既是轴对称图形,又是中心对称图形; 19.计算 32 1 2 5 的结果估计在 ( ) 2 A.6 至 7 之间 B.7 至 8 之间 C.8 至 9 之间 D.9 至 10 之间 20.用配方法解一元二次方程 4x2 1 2 4x 1,变形正确的是 ( )A.(x ) 0 2 B. ( x 1)2 2 1 C. (x 2 1)2 0 D. (x 1)2 0 三.解答题(本大题共 8 小题,满分 60 分.解答应写出文字说明 .证明过程或演算步骤) 21.计算: 80 - 4 1 ) -( 5 3 1 + 4 5 5 45 ) (4 分) 1 1 x 1 22.先化简,再求值: 2 2 ,其中 x 3 1. (4 分) x 1 x 1 x 2x 1 23.解方程: 9( x-1) 2 - 8 = 0 (4 分) 24.如图所示的格图中, 每小格都是边长为 1 的正方形, △ ABC 的三个顶点都在格点上, 在建立直角坐标系 后,点 C 的坐标( -1, 2)、 ( 1).画出△ ABC 绕点 D(0,5)逆时针旋转 90°后的△ A1B1C1,(2 分) ( 2).写出 A1,C1 的坐标。 (2 分) ( 3).求点 A 旋转到 A1 所经过的路 (2 分) 25.有一人患了流感,经过两轮传染后共有 121 人患了流感,每轮传染中平均一个人传染了几个人? ( 8 分) 26. 一个家庭有 3 个孩子,(1)求这个家庭有 2 个男孩和 1 个女孩的概率; (2)求这个家庭至少有一个男 孩 的概率。 (8 分) 27.已知, AB 为⊙ O 的直径,点 E 为弧 AB 任意一点,如图, AC 平分∠ BAE,交⊙ O 于 C ,过点 C 作 CD⊥AE 于 D,与 AB的延长线交于 P. ⑴ 求证: PC 是⊙ O 的切线.(5 分)⑵ ∠BAE=60°,求线段 PB 与 AB数量关系.( 5 分) 28.直径为 2 m 的圆形纸片,要从中剪去一个最大的圆心角是 90°的扇形 ABC (1).求被剪掉的阴影部分的面积; (5 分) (2).用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少? (6 分) (3).求圆锥的全面积. (5 分) 温馨提示:恭喜你已经解答完所有问题,请再仔细检查一次,预祝你取得好成绩!查看更多