- 2021-06-18 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学中考总复习课件PPT:第25课时 点、直线与圆的位置关系
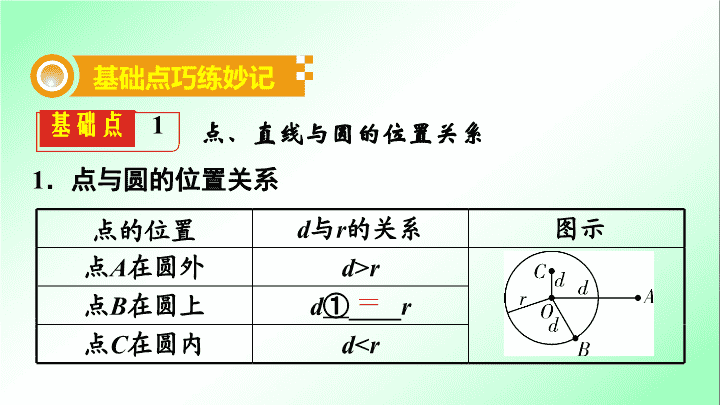
第一部分 夯实基础 提分多 第 六 单元 圆 第 2 5 课时 点、直线与圆的位置关系 基础点 1 点、直线与圆的位置关系 基础点巧练妙记 1 .点与圆的位置关系 点的位置 d 与 r 的关系 图示 点 A 在圆外 d > r 点 B 在圆上 d ① ____ r 点 C 在圆内 d < r = 2. 直线与圆的位置关系 设圆的半径为 r ,圆心到直线的距离为 d 直线与圆的位置关系 d 与 r 的关系 交点的个数 示意图 相离 d > r 没有公共交点 直线与圆的位置关系 d 与 r 的关系 交点的个数 示意图 相切 d = r 有且只有 ② ______ 公共点 相交 ③ ______ 有两个公共点 一个 d < r 1 .已知⊙ O 的半径是 4 , OP = 3 ,则点 P 与⊙ O 的位置关系是 ( ) A .点 P 在圆内 B .点 P 在圆上 C .点 P 在圆外 D .不能确定 2 .已知⊙ O 的半径为 3 ,圆心 O 到直线 L 的距离为 2 ,则直线 L 与⊙ O 的位置关系是 ( ) A .相交 B .相切 C .相离 D .不能确定 练 提 分 必 A A 基础点 2 切线的性质与判定 1. 定义 :直线和圆有 ④ ______ 公共点时,这条直线叫做圆的切线. 2. 性质 :圆的切线垂直于过 ⑤ ______ 的半径. 3. 判定方法 (1) 已知切点:连接圆心和切点的半径,证明半径与要证的切线垂直,即“连半径,证垂直”. 一个 切点 (2) 未知切点:过圆心作出要证切线的垂线段,证明垂线 段的长等于半径,即“作垂线,证相等”. 4 . 切线长 :经过圆外一点作圆的切线,这点和 ⑥ _____ 之间线段的长,叫做这点到圆的切线长. 切点 5 . 切线长定理 从圆外一点可以引圆的 ⑦ _____ 条切线,它们的切线长 ⑧ ______ ,这一点和圆心的连线平分两条切线的夹角.如图, PA 、 PB 切⊙ O 于 A 、 B 两点,则有 PA = PB ,∠ APO = ⑨ ______ = ∠ APB . 相等 ∠ BPO 两 基础点 3 三角形的外接圆与内切圆 名称 三角形的外接圆 三角形的内切圆 圆心名称 三角形的外心 三角形的内心 描述 经过三角形的三个顶点的圆,外心是三角形三条边垂直平分线的交点 与三角形各边都相切的圆,内心是三角形三条角平分线的交点 名称 三角形的外接圆 三角形的内切圆 图形 性质 三角形的外心到三角形三个顶点的距离相等 三角形的内心到三角形三边的距离相等 重难点精讲优练 例 (2017 麓山国际实验学校三模 ) 如图,已知 AB 为⊙ O 的直径,点 E 在⊙ O 上,∠ EAB 的平分线交⊙ O 于点 C ,过点 C 作 AE 的垂线,垂足为 D ,直线 DC 与 AB 的延长线交于点 P. (1) 判断直线 PC 与⊙ O 的位置关系,并说明理由; 例 (2017 麓山国际实验学校三模 ) 如图,已知 AB 为⊙ O 的直径,点 E 在 ⊙ O 上,∠ EAB 的平分线交 ⊙ O 于点 C ,过点 C 作 AE 的垂线,垂足为 D , 直线 DC 与 AB 的延长线交于点 P. (1) 判断直线 PC 与 ⊙ O 的位置关系,并说明理由; 【思维教练】 连接 OC ,要证 PC 是 ⊙ O 的切线,已 AD ⊥ DP ,只要证明 OC//AD ,推出 ∠ OCP =∠ D =90 °,即可得证 解: (1) PC 是 ⊙ O 的切线. 理由:如解图,连接 OC . ∵ AC 平分∠ EAB ,∴∠ EAC =∠ CAB , 又∵ OA = OC ,∴∠ CAB =∠ ACO , ∴∠ EAC =∠ OCA ,∴ OC ∥ AD . ∵ AD ⊥ PD ,∴ OC ⊥ PD ,又∵ OC 是 ⊙ O 的半径, ∴ PC 是 ⊙ O 的切线; 例解图 (2) 若 tan ∠ P = , AD = 6 ,求线段 AE 的长. 【 思维教练 】 由 OC ∥ AD , 推出 = , 即 = , 连接 BE . 由 ∠ AEB = 90° , 推出 BE ∥ PD ,∠ ABE = ∠ P , AE = AB · sin ∠ ABE = AB · sin ∠ P , 由此计算即可. 解: (2) 如解图,连接 BE . 在 Rt △ ADP 中,∠ ADP = 90° , AD = 6 , tan ∠ P = , ∴ PD = 8 , AP = 10. 设半径为 r ,则 OP = AP - AO = 10 - r , ∵ OC ∥ AD , ∴ = ,即 = , 解得 r = . ∵ AB 是直径, ∴∠ AEB =∠ D = 90° ,∴ BE ∥ PD , ∴∠ ABE =∠ P , ∴在 Rt △ ABE 中, AE = AB · sin ∠ ABE = AB · sin ∠ P = ×2× = . 练习 1 如图,已知 AB 是 ⊙ O 的直径,点 C 在 ⊙ O 上,过点 C 的切线与 AB 的延长线交于点 P ,连接 AC . 若 ∠ A = 30 ° , PC = 3 ,则 BP 的长为 ________ . 练习 1 题图 【 解析 】 如解图,连接 OC ,∵ OA = OC ,∠ A = 30° ,∴∠ OCA =∠ A = 30° ,∴∠ COB =∠ A +∠ ACO = 60°.∵ PC 是⊙ O 的切线,∴∠ PCO = 90° ,∠ P = 30°.∵ PC = 3 ,∴ OC = PC · tan 30° = 3× = , PO = 2 OC = 2 ,∴ PB = PO - OB = . 练习 1 解图 练习 2 (2017 株洲 ) 如图,已知 AM 是 ⊙ O 的直径,直线 BC 经过点 M ,且 AB = AC , ∠ BAM = ∠ CAM ,线段 AB 和 AC 分别交 ⊙ O 于点 D 、 E , ∠ BMD = 40 ° ,则 ∠ EOM = ________ 度. 练习 2 题图 【 解析 】 ∵ AB = AC ,∠ BAM =∠ CAM ,∴ AM ⊥ BC , ∴∠ AMD +∠ BMD = 90° ,∴∠ AMD = 50°. ∵ AM 是直径,∴∠ ADM = 90° ,∠ AMD +∠ DAM = 90° , ∴∠ DAM = 40° ,∴∠ MAE = 40° , ∴∠ EOM = 2∠ MAE = 80°. 练习 3 如图, AB 是 ⊙ O 的直径,点 C 在 ⊙ O 上, AD 和过 C 点的切线互相垂直,垂足为 D . (1) 求证: AC 平分 ∠ DAB ; (2) 若点 M 是的中点, CM 交 AB 于点 N , ⊙ O 的半径为 R ,求 MN · MC 的值. 练习 3 题图 【 解析 】 (1)证明:如解图,连接 OC , ∵ CD 是 ⊙ O 的切线 ,∴ OC ⊥ CD . 又 ∵ AD ⊥ CD ,∴ OC ∥ AD , ∴∠ OCA = ∠ DAC. ∵ OA = OC , ∴∠ OAC = ∠ OCA , ∴∠ DAC = ∠ OAC ,即 AC 平分 ∠ DAB ; 练习 3 解图 (2) 解: 如解图,连接 MA , ∵点 M 是的中点, ∴ MA = MB ,∠ MAB =∠ MBA , 又∵∠ MBA =∠ MCA , ∴∠ MAN =∠ MCA , 又∵∠ NMA =∠ AMC , ∴△ NMA ∽△ AMC , 练习 3 解图 ∴ = , ∴ MN·MC = MA 2 . ∵ AB 是⊙ O 的直径, MA = MB, ∴△ MAB 是等腰直角三角形, ∴ MA 2 + MB 2 = AB 2 = (2 R ) 2 ,即 2 MA 2 = 4 R 2 , ∴ MN·MC = MA 2 = 2 R 2 . 练习 3 解图查看更多