高中数学必修2教案：几何体的结构 三视图和直观图及柱体 锥体与台体的表面积

高中数学必修2教案：几何体的结构 三视图和直观图及柱体 锥体与台体的表面积

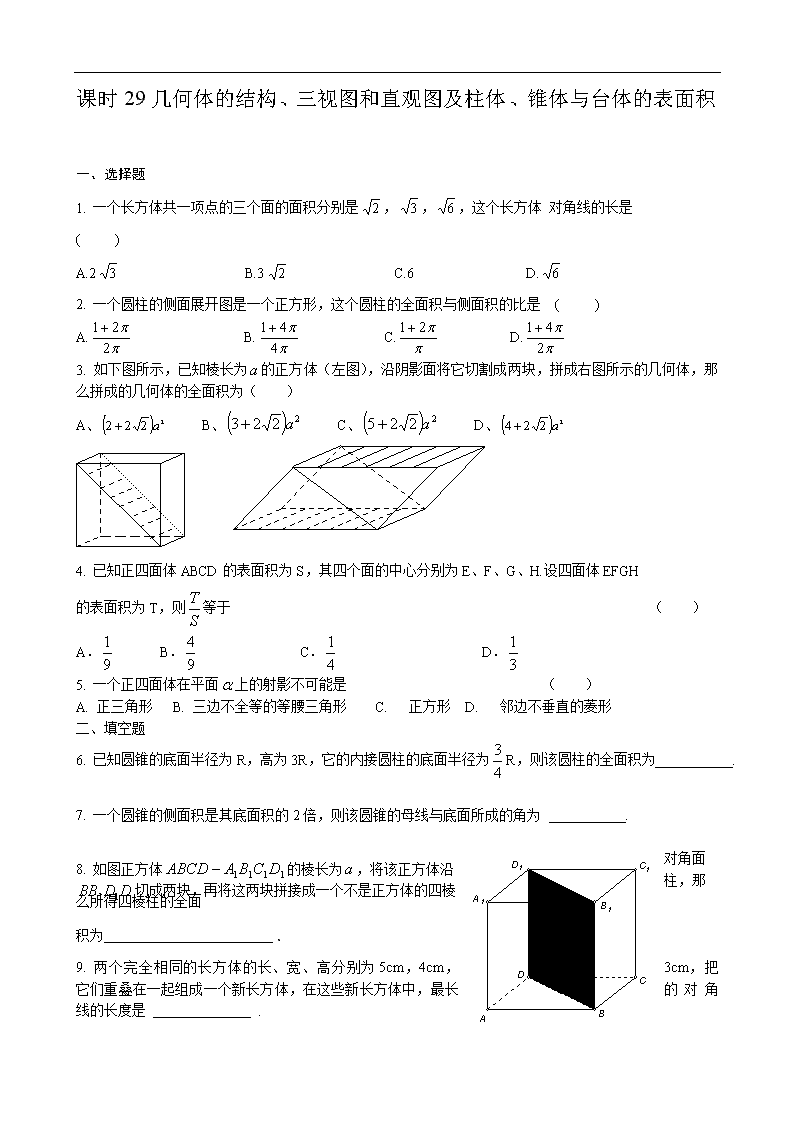
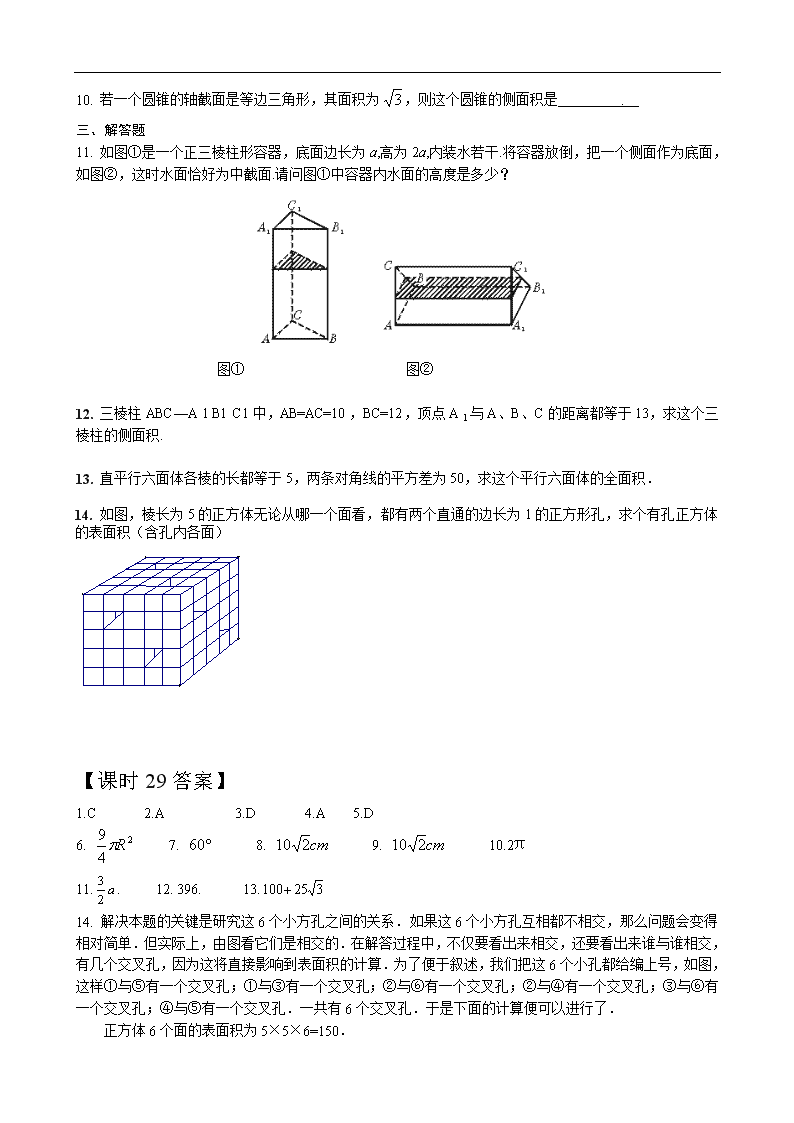
课时29几何体的结构、三视图和直观图及柱体、锥体与台体的表面积 一、选择题 ‎1. 一个长方体共一项点的三个面的面积分别是，，，这个长方体 对角线的长是 ( )‎ A.2 B‎.3‎ C.6 D.‎ ‎2. 一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是 ( )‎ A. B. C. D.‎ ‎3. 如下图所示，已知棱长为的正方体（左图），沿阴影面将它切割成两块，拼成右图所示的几何体，那么拼成的几何体的全面积为（ ）‎ A、 B、 C、 D、‎ ‎ ‎ ‎4. 已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H.设四面体EFGH 的表面积为T，则等于 （ ）‎ A． B． C． D．‎ ‎5. 一个正四面体在平面上的射影不可能是 （ ）‎ A. 正三角形 B. 三边不全等的等腰三角形 C. 正方形 D. 邻边不垂直的菱形 ‎ 二、填空题 ‎6. 已知圆锥的底面半径为R，高为3R，它的内接圆柱的底面半径为R，则该圆柱的全面积为 . ‎ ‎7. 一个圆锥的侧面积是其底面积的2倍，则该圆锥的母线与底面所成的角为 .‎ ‎8. 如图正方体的棱长为，将该正方体沿对角面切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面 积为 ．‎ ‎9. 两个完全相同的长方体的长、宽、高分别为‎5cm，‎4cm，‎3cm，把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度是 .‎ ‎10. 若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的侧面积是 . ‎ 三、解答题 ‎11. 如图①是一个正三棱柱形容器，底面边长为a,高为‎2a,内装水若干.将容器放倒，把一个侧面作为底面，如图②，这时水面恰好为中截面.请问图①中容器内水面的高度是多少？‎ ‎ ‎ 图① 图②‎ ‎12. 三棱柱ABC—A 1 B‎1 C1中，AB=AC=10，BC=12，顶点A 1与A、B、C的距离都等于13，求这个三棱柱的侧面积.‎ ‎13. 直平行六面体各棱的长都等于5，两条对角线的平方差为50，求这个平行六面体的全面积．‎ ‎14. 如图，棱长为5的正方体无论从哪一个面看，都有两个直通的边长为1的正方形孔，求个有孔正方体的表面积（含孔内各面）‎ ‎【课时29答案】‎ ‎1.C 2.A 3.D 4.A 5.D ‎6. 7. 8. 9. 10.2π ‎11.. 12. 396. 13.‎ ‎14. 解决本题的关键是研究这6个小方孔之间的关系．如果这6个小方孔互相都不相交，那么问题会变得相对简单．但实际上，由图看它们是相交的．在解答过程中，不仅要看出来相交，还要看出来谁与谁相交，有几个交叉孔，因为这将直接影响到表面积的计算．为了便于叙述，我们把这6个小孔都给编上号，如图，这样①与⑤有一个交叉孔；①与③有一个交叉孔；②与⑥有一个交叉孔；②与④有一个交叉孔；③与⑥有一个交叉孔；④与⑤有一个交叉孔．一共有6个交叉孔．于是下面的计算便可以进行了．‎ ‎ 正方体6个面的表面积为5×5×6=150．‎ ‎ 每个面有2个小正方形，6个面，共有=1 2．‎ ‎ 每一个孔的内表面积为4×5=20，6个孔为20×6=1 20．‎ ‎ 每个交叉孔的表面积为6，6个孔为6×6=36．‎ ‎ 所以150－1 2+120－36=222为所求． ‎ ‎ ‎