- 2021-06-04 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江专用2021届高考数学一轮复习第二章不等式2-1不等式及其解法课件
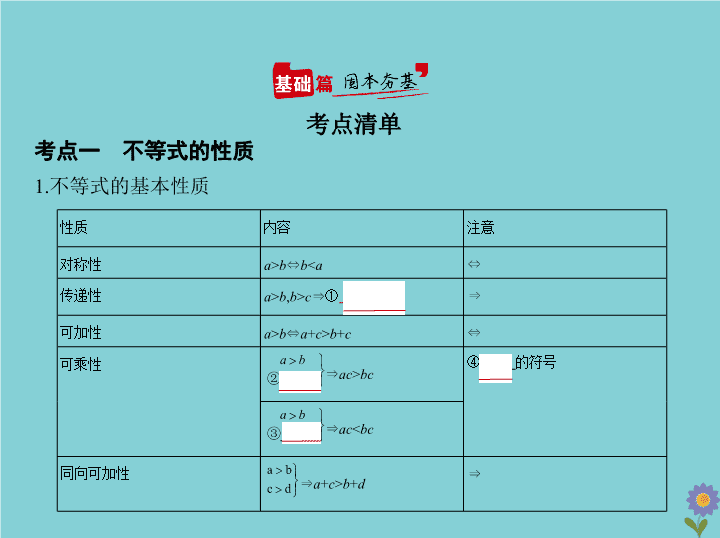
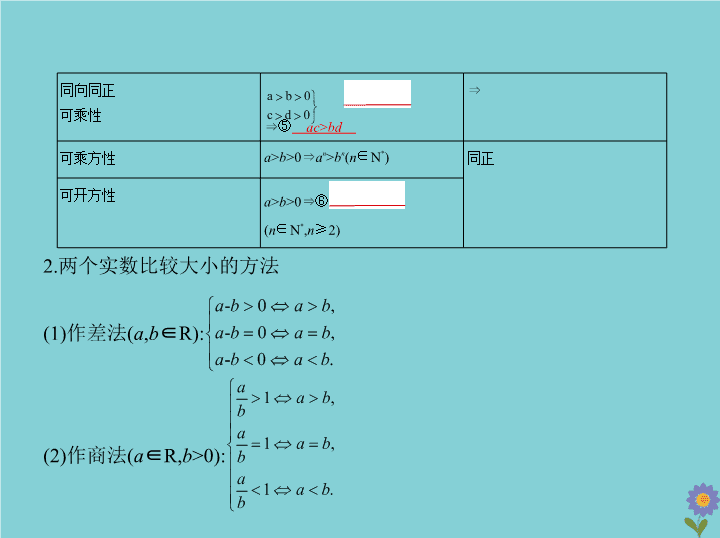
第二章 不等式 §1.1 不等式及其解法 高考数学 考点一 不等式的性质 1.不等式的基本性质 考点 清单 性质 内容 注意 对称性 a > b ⇔ b < a ⇔ 传递性 a > b , b > c ⇒ ① a > c ⇒ 可加性 a > b ⇔ a + c > b + c ⇔ 可乘性 ⇒ ac > bc ④ c 的符号 ⇒ ac < bc 同向可加性 ⇒ a + c > b + d ⇒ 同向同正 可乘性 ⇒ ⑤ ac > bd ⇒ 可乘方性 a > b >0 ⇒ a n > b n ( n ∈N * ) 同正 可开方性 a > b >0 ⇒ ⑥ > ( n ∈N * , n ≥ 2) 2.两个实数比较大小的方法 (1)作差法( a , b ∈R): (2)作商法( a ∈R, b >0): 3.不等式的倒数和分式性质 (1)倒数性质:(i) a > b , ab >0 ⇒ ⑦ < ; (ii) a <0< b ⇒ < . (2)有关分式的性质:若 a > b >0, m >0,则 (i) <⑧ ; > ( b - m >0). (ii) > ; <⑨ ( b - m >0). 考点二 不等式的解法 1.一元二次不等式与相应的二次函数及一元二次方程的关系 判别式 Δ = b 2 -4 ac Δ >0 Δ =0 Δ <0 二次函数 y = ax 2 + bx + c ( a >0)的图象 一元二次方程 ax 2 + bx + c =0( a >0)的根 有两个相异实根 x 1 , x 2 ( x 1 < x 2 ) 有两个相等实根 x 1 = x 2 =- 没有实根 ax 2 + bx + c >0( a >0)的解集 ⑩ { x | x < x 1 或 x > x 2 } x x ≠ - R ax 2 + bx + c <0( a >0)的解集 { x | x 1 < x < x 2 } ⌀ ⌀ 在不等式 ax 2 + bx + c >0( a ≠ 0)中,如果二次项系数 a <0,则可先根据不等式 的性质,将其转化为正数,再对照上表求解. 2.分式不等式的解法 (1) >0(<0) ⇔ f ( x )· g ( x )>0(<0); (2) ≥ 0( ≤ 0) ⇔ 3.绝对值不等式的解法 (1)| f ( x )|>| g ( x )| ⇔ [ f ( x )] 2 >[ g ( x )] 2 ; (2)| f ( x )|> g ( x ) ⇔ f ( x )> g ( x )或 f ( x )<- g ( x ) ; (3)| f ( x )|< g ( x ) ⇔ - g ( x )< f ( x )< g ( x ) ; (4)含两个或两个以上绝对值符号的不等式可用 零点分区间 的方法脱去绝 对值符号求解,也可以用图象法求解. 考法一 不等式性质的应用 知能拓展 例1 (2018湖南衡阳一模,4)若 a , b , c 为实数,且 a < b <0,则下列结论正确的是 ( ) A. ac 2 < bc 2 B. < C. > D. a 2 > ab > b 2 解题导引 观察本题条件与选项的特点,能想到考点清单中的哪些?可以 想到不等式的性质,比较大小的方法等.因此本题可采用以上两种思路求 解.作为选择题还可以用特值法求解. 解析 选项A,∵ c 为实数,∴取 c =0,得 ac 2 =0, bc 2 =0,此时 ac 2 = bc 2 ,故选项A不正 确;选项B, - = ,∵ a < b <0,∴ b - a >0, ab >0,∴ >0,即 > ,故选项B不正 确;选项C,∵ a < b <0,∴取 a =-2, b =-1,则 = = , =2,此时 < ,故选项C不正 确;选项D,∵ a < b <0,∴ a 2 - ab = a ( a - b )>0,∴ a 2 > ab ,又∵ ab - b 2 = b ( a - b )>0,∴ ab > b 2 , 故选项D正确,故选D. 答案 D 方法总结 作差法比较大小的步骤:①作差;②变形:通分,因式分解,分子 (母)有理化,写成因式积(商)的形式;③判断符号;④下结论. 考法二 不等式的解法 例2 (2019河南濮阳3月模拟,7)已知不等式 ax 2 + bx + c >0的解集是{ x | α < x < β } ( α >0),则不等式 cx 2 + bx + a <0的解集是 ( ) A. B. ∪ C.{ x | α < x < β } D.(- ∞ , α ) ∪ ( β ,+ ∞ ) 解题导引 由题设可知 a <0,且 α , β 是方程 ax 2 + bx + c =0的两根,由根与系数的 关系可得出 a , b , c 与 α , β 的数量关系,即 注意 c <0,再把方程 cx 2 + bx + a =0的根用 α , β 表示出来即可求得结果. 解析 由不等式 ax 2 + bx + c >0的解集是{ x | α < x < β }( α >0),得 α , β 是一元二次方 程 ax 2 + bx + c =0的实数根,且 a <0,∴ α + β =- , αβ = .不等式 cx 2 + bx + a <0可化为 x 2 + x +1>0,∴ αβx 2 -( α + β ) x +1>0,化为( αx -1)( βx -1)>0,又0< α < β ,∴ > >0, c = a αβ <0,∴不等式 cx 2 + bx + a <0的解集为 ,故选B. 答案 B 方法总结 若一元二次不等式 ax 2 + bx + c >0(或<0)的解集为{ x | x > x 2 或 x < x 1 }( x 1 < x 2 ),则 a >0(或 a <0), Δ >0且 x 1 , x 2 是方程 ax 2 + bx + c =0( a ≠ 0)的两个实根;若一元 二次不等式 ax 2 + bx + c >0(或<0)的解集为{ x | x 1 < x < x 2 },则 a <0(或 a >0), Δ >0且 x 1 , x 2 是方程 ax 2 + bx + c =0( a ≠ 0)的两个实根.查看更多