2014-2018年五年真题分类第七章 不等式

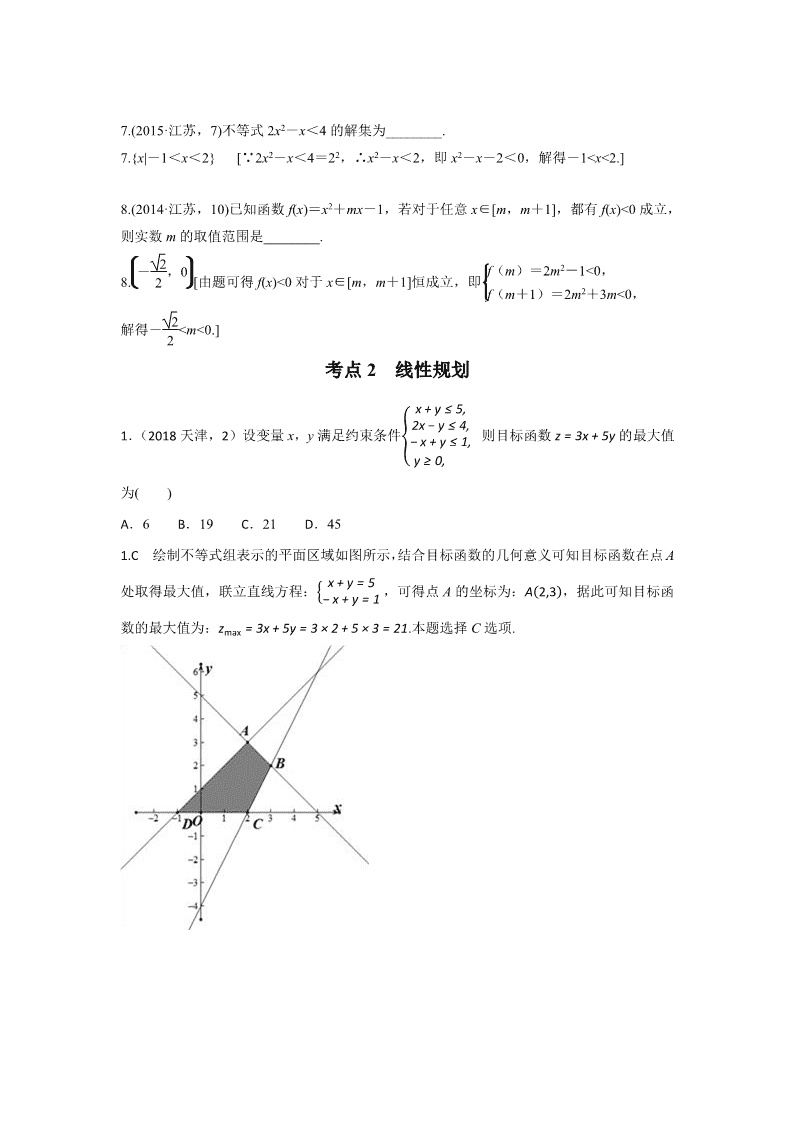
2014-2018年五年真题分类第七章 不等式

第七章 不等式 考点 1 不等关系与不等式 1.（2017•山东,7）若 a＞b＞0，且 ab=1，则下列不等式成立的是（　　） A.a+ ＜ ＜log2（a+b） B. ＜log2（a+b）＜a+ C.a+ ＜log2（a+b）＜ D.log2（a+b））＜a+ ＜ 1. B ∵a＞b＞0，且 ab=1， ∴可取 a=2，b= ．则 = ， = = ，log 2 （a+b）= = ∈（1，2），∴ ＜log2（a+b）＜a+ ．故选 B． 2.（2017·天津,8）已知函数 f（x）= ，设 a∈R，若关于 x 的不等式 f（x） ≥| +a|在 R 上恒成立，则 a 的取值范围是（　　） A.[﹣ ，2] B.[﹣ ， ] C.[﹣2 ，2] D.[﹣2 ， ] 2. A 当 x≤1 时，关于 x 的不等式 f（x）≥| +a|在 R 上恒成立， 即为﹣x2+x﹣3≤ +a≤x2﹣x+3， 即有﹣x2+ x﹣3≤a≤x2﹣ x+3， 由 y=﹣x2+ x﹣3 的对称轴为 x= ＜1，可得 x= 处取得最大值﹣ ； 由 y=x2﹣ x+3 的对称轴为 x= ＜1，可得 x= 处取得最小值 ， 则﹣ ≤a≤ ① 当 x＞1 时，关于 x 的不等式 f（x）≥| +a|在 R 上恒成立， 即为﹣（x+ ）≤ +a≤x+ ， 即有﹣（ x+ ）≤a≤ + ， 由 y=﹣（ x+ ）≤﹣2 =﹣2 （当且仅当 x= ＞1）取得最大值﹣2 ； 由 y= x+ ≥2 =2（当且仅当 x=2＞1）取得最小值 2． 则﹣2 ≤a≤2② 由①②可得，﹣ ≤a≤2． 故选 A． 3.(2016·北京,5)已知 x,y∈R,且 x＞y＞0,则(　　) A. 1 x－ 1 y＞0 B.sinx－sin y＞0 C.(1 2 ) x －(1 2 ) y ＜0 D.lnx＋lny＞0 3.C [函数 y＝1 x在(0,＋∞)上单调递减,所以1 x＜1 y,即1 x－1 y＜0,A 错;函数 y＝sin x 在(0,＋∞)上不 是单调函数,B 错;函数 y＝(1 2 )x 在(0,＋∞)上单调递减,所以(1 2 )x ＜(1 2 )y ,即(1 2 )x － (1 2 )y ＜0,所以 C 正确；lnx＋lny＝lnxy,当 x＞y＞0 时,xy 不一定大于 1,即不一定有 lnxy＞0,D 错.] 4. (2016·全国Ⅰ,8)若 a>b>1,0b>1⇒ac>bc,故 A 错； 对 B：由于－1b>1⇔ac－11), 则 f′(x) ＝ lnx ＋ 1>1>0,f(x) 在 (1, ＋ ∞) 上 单 调 递 增 , 因 此 f(a)>f(b)>0⇒aln a>blnb>0⇒ 1 aln a< 1 bln b,又由 0 ln c bln b⇒blogac>alogbc,C 正 确； 对 D：要比较 logac 和 logbc,只需比较 ln c ln a和ln c ln b,而函数 y＝lnx 在(1,＋∞)上单调递增,故 a>b>1⇔ln a>lnb>0⇔ 1 ln a< 1 ln b,又由 0ln c ln b⇔logac>logbc,D 错误,故选 C.] 5.(2014·四川,4)若 a>b>0,cb d B.a cb c D.a d－1 c>0,又 a>b>0,故由不等式性质,得－a d>－b c>0,所以a d9 6.C [由题意，不妨设 g(x)＝x3＋ax2＋bx＋c－m，m∈(0，3]，则 g(x)的三个零点分别为 x1＝－ 3，x2＝－2，x3＝－1，因此有(x＋1)(x＋2)(x＋3)＝x3＋ax2＋bx＋c－m，则 c－m＝6，因此 c ＝m＋6∈(6，9].] 7.(2015·江苏，7)不等式 2x2－x＜4 的解集为________. 7.{x|－1＜x＜2} [∵2x2－x＜4＝22，∴x2－x＜2，即 x2－x－2＜0，解得－1zC 或 zA＝zC>zB 或 zB＝zC>zA,解得 a ＝－1 或 a＝2. 法二　目标函数 z＝y－ax 可化为 y＝ax＋z,令 l0：y＝ax,平移 l0,则当 l0∥AB 或 l0∥AC 时符合 题意,故 a＝－1 或 a＝2.] 16.(2014·山东,9)已知x,y满足约束条件Error!当目标函数z＝ax＋by(a>0,b>0)在该约束条件下 取到最小值 2 5时,a2＋b2 的最小值为(　　) A.5 B.4 C. 5 D.2 16.B [法一　不等式组表示的平面区域如图所示,根据目标函数的几何意义可知,目标函数 在点 A(2,1)处取得最小值,故 2a＋b＝2 5,两端平方得 4a2＋b2＋4ab＝20,又 4ab＝2×a×2b≤a2＋ 4b2,所以20≤4a 2＋b2＋a2＋4b2＝5(a2＋b2),所以a 2＋b2≥4,即a 2＋b2的最小值为4,当且仅当a＝ 2b,即 b＝ 2 5,a＝ 4 5时等号成立. 法二　把 2a＋b＝2 5看作平面直角坐标系 aOb 中的直线,则 a2＋b2 的几何意义是直线上的 点与坐标原点距离的平方,显然 a2＋b2 的最小值是坐标原点到直线 2a＋b＝2 5距离的平方, 即(|－2 5| 5 ) 2 ＝4.] 17.(2014·新课标全国Ⅰ,9)不等式组Error!的解集记为 D.有下面四个命题： p1：∀(x,y)∈D,x＋2y≥－2,p2：∃(x,y)∈D,x＋2y≥2, p3：∀(x,y)∈D,x＋2y≤3,p4：∃(x,y)∈D,x＋2y≤－1. 其中的真命题是(　　) A.p2,p3 B.p1,p4 C.p1,p2 D.p1,p3 17.C[画出可行域如图中阴影部分所示,由图可知,当目标函数z＝x＋2y经过可行域内的点A(2, －1)时,取得最小值 0,故 x＋2y≥0,因此 p1,p2 是真命题,选 C.] 18 ．（ 2018 全 国 Ⅰ ， 13 ） 若 x， y满 足 约 束 条 件 {x−2y−2 ≤ 0 x−y + 1 ≥ 0 y ≤ 0 ， 则 z = 3x + 2y的 最 大 值 为 _____________． 18.6 根据题中所给的约束条件，画出其对应的可行域，如图所示： 由z = 3x + 2y可得y = −3 2x + 1 2z，画出直线y = −3 2x，将其上下移动，结合z 2的几何意义，可知当直 线过点 B 时，z 取得最大值，由{x−2y−2 = 0 y = 0 ，解得B(2,0)，此时zmax = 3 × 2 + 0 = 6，故答案为 6. 19 ．（ 2018 全 国 Ⅱ ， 14 ） 若 x, y满 足 约 束 条 件 {x + 2y−5 ≥ 0, x−2y + 3 ≥ 0, x−5 ≤ 0, 则 z = x + y的 最 大 值 为 __________． 19.9 不等式组表示的可行域是以A(5,4),B(1,2),C(5,0)为顶点的三角形区域，如下图所示，目 标函数z = x + y的最大值必在顶点处取得，易知当x = 5,y = 4时，zmax = 9. 20．（2018 浙江，12）若x,y满足约束条件{ x−y ≥ 0, 2x + y ≤ 6, x + y ≥ 2, 则z = x + 3y的最小值是___________，最 大值是___________． 20. -2 8 作可行域，如图中阴影部分所示，则直线z = x + 3y过点 A(2,2)时z取最大值 8， 过点 B(4,-2)时z取最小值-2. 21．（2018 北京，12）若 x，y 满足 x+1≤y≤2x，则 2y−x 的最小值是__________． 21.3 作可行域，如图，则直线z = 2y−x过点 A(1,2)时，z取最小值 3. 22.（2017•新课标Ⅰ,14）设 x，y 满足约束条件 ，则 z=3x﹣2y 的最小值为 ________． 22. -5 由 x，y 满足约束条件 作出可行域如图， 由图可知，目标函数的最优解为 A，联立 ，解得 A（﹣1，1）． ∴z=3x﹣2y 的最小值为﹣3×1﹣2×1=﹣5．故答案为：﹣5． 23.（2017•新课标Ⅲ,13）若 x，y 满足约束条件 ，则 z=3x﹣4y 的最小值为 ________ 23.﹣1 由 z=3x﹣4y，得 y= x﹣ ，作出不等式对应的可行域（阴影部分）， 平移直线 y= x﹣ ，通过平移可知当直线 y= x﹣ ， 经过点 B（1，1）时，直线 y= x﹣ 在 y 轴上的截距最大，此时 z 取得最小值， 将 B 的坐标代入 z=3x﹣4y=3﹣4=﹣1， 即目标函数 z=3x﹣4y 的最小值为﹣1． 故答案为：﹣1． 24. （ 2017• 山 东 ,10 ） 已 知 满 足 ， 则 的 最 大 值 是 __________． 24. 5 画出约束条件表示的平面区域，如图所示； 由 解得 A（﹣3，4），此时直线 y=﹣ x+ z 在 y 轴上的截距最大， 所以目标函数 z=x+2y 的最大值为 zmax=﹣3+2×4=5．故选 C． 25.(2016·全国Ⅲ,13)若 x,y 满足约束条件{x－y＋1 ≥ 0， x－2y ≤ 0， x＋2y－2 ≤ 0， 则 z＝x＋y 的最大值为________. ,x y 3 0 {3 5 0 3 0 x y x y x − + ≤ + + ≤ + ≥ 2z x y= + 25.3 2 [满足约束条件{x－y＋1 ≥ 0， x－2y ≤ 0， x＋2y－2 ≤ 0 的可行域为以 A(－2,－1),B(0,1),C (1，1 2 )为顶点的三角 形内部及边界,过 C (1，1 2 )时取得最大值为3 2.] 26.(2016·全国Ⅰ,16)某高科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料.生产一件 产品 A 需要甲材料 1.5 kg,乙材料 1 kg,用 5 个工时；生产一件产品 B 需要甲材料 0.5 kg,乙材 料 0.3 kg,用 3 个工时,生产一件产品 A 的利润为 2 100 元,生产一件产品 B 的利润为 900 元.该 企业现有甲材料 150 kg,乙材料 90 kg,则在不超过 600 个工时的条件下,生产产品 A、产品 B 的利润之和的最大值为________元. 26. 216 000 [设生产 A 产品 x 件,B 产品 y 件,根据所耗费的材料要求、工时要求等其他限制 条件,得线性约束条件为{1.5x＋0.5y ≤ 150， x＋0.3y ≤ 90， 5x＋3y ≤ 600， x ≥ 0， y ≥ 0， x ∈ N * ， y ∈ N * 目标函数 z＝2 100x＋900y. 作出可行域为图中的四边形,包括边界,顶点为(60,100),(0,200),(0,0),(90,0),在(60,100)处取得最 大值,zmax＝2 100×60＋900×100＝216 000(元).] 27.(2015·新课标全国Ⅰ,15)若 x,y 满足约束条件Error!则y x的最大值为________. 27.3[约束条件的可行域如下图,由 y x＝ y－0 x－0,则最大值为 3.] 28.(2014·大纲全国,14)设 x、y 满足约束条件Error!则 z＝x＋4y 的最大值为________. 28.5 [作出约束条件下的平面区域,如图所示.由图可知当目标函数 z＝x＋4y 经过点 B(1,1)时 取得最大值,且最大值为 1＋4×1＝5.] 29.(2014·湖南,14)若变量 x,y 满足约束条件Error!且 z＝2x＋y 的最小值为－6,则 k＝ ________. 29.－2 [画出可行域(图略),由题意可知不等式组表示的区域为一三角形,平移参照直线 2x＋y ＝0,可知在点(k,k)处 z＝2x＋y 取得最小值,故 zmin＝2k＋k＝－6.解得 k＝－2.] 考点 3 基本不等式 1．（2018 全国Ⅲ，12）设a = log0.20.3，b = log20.3，则(　　) A．a + b < ab < 0 B．ab < a + b < 0 C．a + b < 0 < ab D．ab < 0 < a + b 1.B ∵ a = log0.20.3,b = log20.3, ∴ 1 a = log0.30.2,1 b = log0.32, ∴ 1 a + 1 b = log0.30.4, ∴ 0 < 1 a + 1 b < 1, 即0 < a + b ab < 1.又 ∵ a > 0,b < 0, ∴ ab < 0,即ab < a + b < 0.故选 B. 2．（2018 天津，13）已知a , b ∈ R，且a−3b + 6 = 0，则2a + 1 8b的最小值为_____________. 2.1 4 由a - 3b + 6 = 0可知a - 3b = -6，且：2a + 1 8b = 2a + 2-3b，因为对于任意 x，2x > 0恒成立，结 合均值不等式的结论可得：2a + 2-3b ≥ 2 × 2a × 2-3b = 2 × 2-6 = 1 4.当且仅当{ 2a = 2-3b a - 3b = 6 ，即{a = -3 b = 1 时等号成立.综上可得2a + 1 8b的最小值为1 4. 3.（2017•江苏,10）某公司一年购买某种货物 600 吨，每次购买 x 吨，运费为 6 万元/次，一 年的总存储费用为 4x 万元．要使一年的总运费与总存储费用之和最小，则 x 的值是 ________． 3.30 由题意可得：一年的总运费与总存储费用之和= +4x≥4×2× =240 （万元）．当且仅当 x=30 时取等号．故答案为：30． 4.（2017·天津,12）若 a，b∈R，ab＞0，则 的最小值为________． 4. 4 a，b∈R，ab＞0， ∴ ≥ = =4ab+ ≥2 =4，当且仅当 ， 即 ，即 a= ，b= 或 a=﹣ ，b=﹣ 时取“=”；∴上式的最小值 为 4．故答案为：4． 5 .(2014·上海，5)若实数 x，y 满足 xy＝1，则 x2＋2y2 的最小值为________． 5.2 2 [∵x2＋2y2≥2 x2·2y2＝2 2xy＝2 2，当且仅当 x＝ 2y 时取“＝”，∴x2＋2y2 的最小 值为 2 2.]