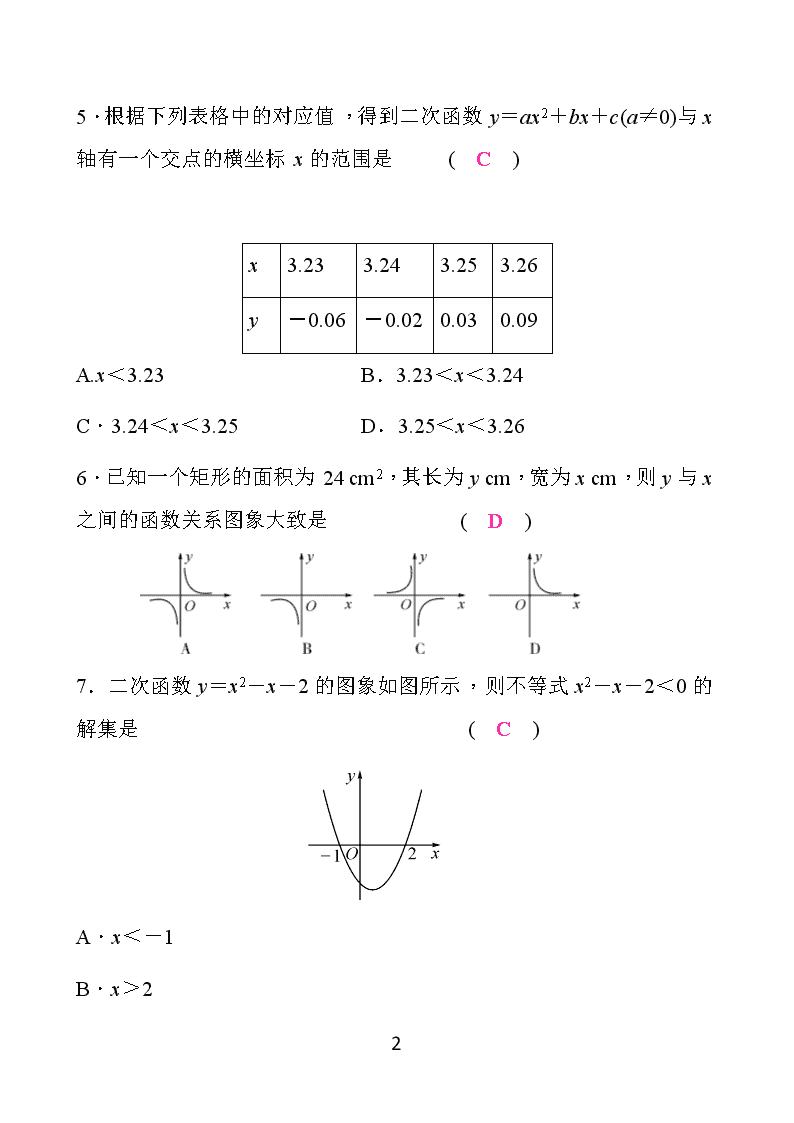沪科版九年级数学上册第21章测试题（含答案）
沪科版九年级数学上册第21章测试题（含答案）
(考试时间：120分钟 满分：150分)
姓名：______ 班级：______ 分数：______
一、选择题(本大题共10小题，每小题4分，满分40分)
每小题都给出A、B、C、D四个选项，其中只有一个是正确的．
1．二次函数y＝－3x2－6x＋5的图象的顶点坐标是 ( B )
A．(1，8) B．(－1，8) C．(－1，2) D．(1，－4)
2．若p＋q＝0，则抛物线y＝x2＋p x＋q必过点 ( D )
A．(－1，1) B．(1，－1) C．(－1，－1) D．(1，1)
3．已知点(3，y1)，(4，y2)，(5，y3)在函数y＝2x2＋8x＋7的图象上，则y1，y2，y3的大小关系是 ( D )
A．y1＞y2＞y3 B．y2＞y1＞y3
C．y2＞y3＞y1 D．y3＞y2＞y1
4．赵州桥的桥拱可以用抛物线的一部分表示，函数关系为y＝－ x2.当水面宽度AB为20 m时，水面与桥拱顶的高度DO等于 ( B )
A．2 m B．4 m C．10 m D．16 m
14
5．根据下列表格中的对应值，得到二次函数y＝ax2＋bx＋c(a≠0)与x轴有一个交点的横坐标x的范围是 ( C )
x
3.23
3.24
3.25
3.26
y
－0.06
－0.02
0.03
0.09
A.x＜3.23 B．3.23＜x＜3.24
C．3.24＜x＜3.25 D．3.25＜x＜3.26
6．已知一个矩形的面积为24 cm2，其长为y cm，宽为x cm，则y与x之间的函数关系图象大致是 ( D )
7．二次函数y＝x2－x－2的图象如图所示，则不等式x2－x－2＜0的解集是 ( C )
A．x＜－1
B．x＞2
14
C．－1＜x＜2
D．x＜－1或x＞2
8．二次函数y＝x2＋4x＋3的图象可以由二次函数y＝x2的图象平移而得到，下列平移正确的是 ( B )
A．先向左平移2个单位，再向上平移1个单位
B．先向左平移2个单位，再向下平移1个单位
C．先向右平移2个单位，再向上平移1个单位
D．先向右平移2个单位，再向下平移1个单位
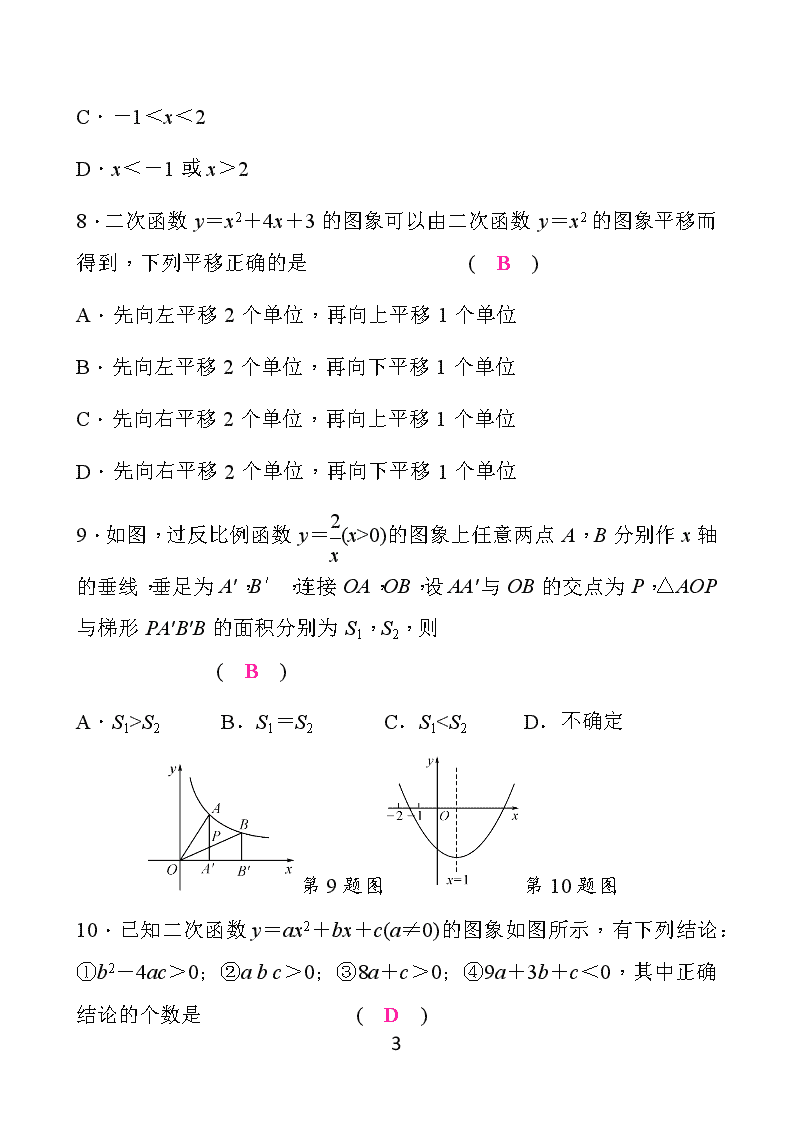
9．如图，过反比例函数y＝(x>0)的图象上任意两点A，B分别作x轴的垂线，垂足为A′，B′，连接OA，OB，设AA′与OB的交点为P，△AOP与梯形PA′B′B的面积分别为S1，S2，则 ( B )
A．S1>S2 B．S1＝S2 C．S1
0，∴k＝6.
(2)∵AB＝2，∴x A＝2，y A＝ ＝3，
∴点A的坐标为(2，3)．
四、(本大题共2小题，每小题8分，满分16分)
17．求满足下列条件的对应的函数的关系式．
(1)抛物线经过(4，0)，(0，－4)，和(－2，3)三点；
14
(2)已知二次函数的图象经过点(0，－3)，且顶点坐标为(1，－4)．
解：(1)设抛物线表达式为y＝ax2＋bx＋c，
将(4，0)，(0，－4)，(－2，3)代入
得
解得
则抛物线表达式为y＝x2－2x－4.
(2)设抛物线表达式为y＝a(x－1)2－4，
将(0，－3)代入得－3＝a－4，即a＝1，
则抛物线表达式为y＝(x－1)2－4＝x2－2x－3.
18．如图所示，一次函数y＝k x＋b的图象与反比例函数y＝－的图象交于A，B两点，且点A的横坐标和点B的纵坐标都是－2，求：
(1)一次函数的关系式；
(2)△AOB的面积．
14
解：(1)设A(x1，y1)，B(x2，y2)，
则x1＝－2，y2＝－2，
把x1＝y2＝－2分别代入y＝得
y1＝x2＝4，∴A(－2，4)，B(4，－2)．
把A(－2，4)和B(4，－2)分别代入y＝k x＋b得解得
∴一次函数的关系式为y＝－x＋2.
(2)∵y＝－x＋2与y轴交点为C(0，2)，∴OC＝2，
∴S△AOB＝S△AOC＋S△BOC
＝×OC×|x1|＋×OC×|x2|
＝×2×2＋×2×4
＝6.
14
即△AOB的面积为6.
五、(本大题共2小题，每小题10分，满分20分)
19．某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件．市场调查反映：如果每件的售价每涨1元(售价每件不能高于45元)，那么每星期少卖10件．设每件涨价x元(x为非负整数)，每星期的销量为y件．
(1)求y与x的函数关系式及自变量x的取值范围；
(2)如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？
解：(1)由题意，得y＝150－10x，0≤x≤5且x为非负整数．
(2)设每星期的利润为w元，
则w＝(40＋x－30)y
＝(x＋10)(150－10x)
＝－10(x－2.5)2＋1 562.5
∵x为非负整数，
∴当x＝2或3时，利润最大为1 560元，
又∵销量较大，
∴x＝2，即当售价为42元时，每周的利润最大且销量较大，最大利润为1 560元．
14
答：当售价为42元时，每星期的利润最大且每星期销量较大，每星期的最大利润为1 560元．
20．如图，函数y1＝k1x＋b的图象与函数y2＝(x＞0)的图象交于点A(2，1)，B，与y轴交于点C(0，3)．
(1)求函数y1的表达式和点B的坐标；
(2)观察图象，指出当x取何值时y1＜y2.(在x＞0的范围内)
解：(1)∵函数y1＝k1x＋b的图象与函数
y2＝(x＞0)的图象交于点A(2，1)，
∴＝1，解得k2＝2，
∴反比例函数表达式为y2＝，
∵函数y1＝k1x＋b经过点A(2，1)，C(0，3)，
∴解得
14
∴y1＝－x＋3，两表达式联立得解得
∴点B的坐标为(1，2)．
(2)根据图象，当0＜x＜1或x＞2时，y1＜y2.
六、(本题满分12分)
21．二次函数y＝ x2－ x＋6的图象与x轴从左到右两个交点依次为A，B，与y轴交于点C.
(1)求A，B，C三点的坐标；
(2)如果P(x，y)是线段BC之间的动点，O为坐标原点，试求△POA的面积S与x之间的函数关系式，并写出自变量x的取值范围；
(3)在(2)的条件下，是否存在这样的点P，使得PO＝PA？若存在，求出点P的坐标；若不存在，请说明理由．
解：(1)A(4，0)，B(6，0)，C(0，6)．
(2)设一次函数的表达式为y＝kx＋b；
将B(6，0)，C(0，6)代入上式，得解得
∴y＝－x＋6.根据题意得S△POA＝×4×y＝－2x＋12，∴0≤x＜6.
(3)存在，理由：
14
∵|OB|＝|OC|，∠COB＝90°，∴△BOC是等腰直角三角形．
作AO的中垂线交CB于P，根据垂直平分线的性质得出PO＝PA，
而OA＝4，∴P点横坐标为2，代入直线BC表达式即可，
∴y＝－x＋6＝－2＋6＝4，∴P点坐标为(2，4)，
∴存在这样的点P(2，4)，使得OP＝AP.
七、(本题满分12分)
22．如图，有长为24米的篱笆，一面利用墙(墙的最大可用长度a为10米)，围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S米2.
(1)求S与x的函数关系式；
(2)如果要围成面积为45米2的花圃，那么AB的长是多少米？
(3)能围成面积比45米2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．
解：(1)由题可知，花圃的宽AB为x米，则BC为(24－3x)米，
∴S＝x(24－3x)＝－3x2＋24x.
(2)当S＝45时，－3x2＋24x＝45，
14
∴x2－8x＋15＝0，解得x1＝5，x2＝3，
∵0＜24－3x≤10得≤x＜8，
∴x＝3不合题意，舍去，∴要围成面积为45米2的花圃，AB的长为5米．
(3)S＝－3x2＋24x＝－3(x2－8x)＝－3(x－4)2＋48，
∴当x＝时，S有最大值48－3＝46.
∴能围成面积比45米2更大的花圃．
围法：花圃的长为10米，宽为4米，这时有最大面积46米2.
八、(本题满分14分)
23．已知抛物线y＝x2＋(2n－1)x＋n2－1(n为常数)．
(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.
①当BC＝1时，求矩形ABCD的周长；
②试问矩形ABCD的周长是否存在最大值？如果存在，
14
请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．
解：(1)由已知条件，得n2－1＝0，
解这个方程，得n1＝1，n2＝－1，
当n＝1时，得y＝x2＋x，此抛物线的顶点不在第四象限．
当n＝－1时，得y＝x2－3x，此抛物线的顶点在第四象限．
∴所求的函数关系式为y＝x2－3x.
(2)由y＝x2－3x，
令y＝0，得x2－3x＝0，解得x1＝0，x2＝3，
∴抛物线与x轴的另一个交点为(3，0)，
∴它的顶点为，对称轴为直线
x＝，其大致位置如图所示，
①∵BC＝1，易知OB＝×(3－1)＝1.
∴B(1，0)，
14
∴点A的横坐标x＝1，又点A在抛物线y＝x2－3x上，
∴点A的纵坐标y＝12－3×1＝－2.
∴AB＝|y|＝|－2|＝2.
∴矩形ABCD的周长为2(AB＋BC)＝2×(2＋1)＝6.
②∵点A在抛物线y＝x2－3x上，故可设A点的坐标为(x，x2－3x)，
∴B点的坐标为(x，0).，∴BC＝3－2x，A在x轴下方，
∴x2－3x＜0，∴AB＝|x2－3x|＝3x－x2，
∴矩形ABCD的周长：
C＝2[(3x－x2)＋(3－2x)]
＝－2＋，
∵a＝－2＜0，抛物线开口向下，二次函数有最大值，
∴当x＝时，矩形ABCD的周长C最大值为.此时点A的坐标为A.
14
