- 2021-05-31 发布 |
- 37.5 KB |
- 16页

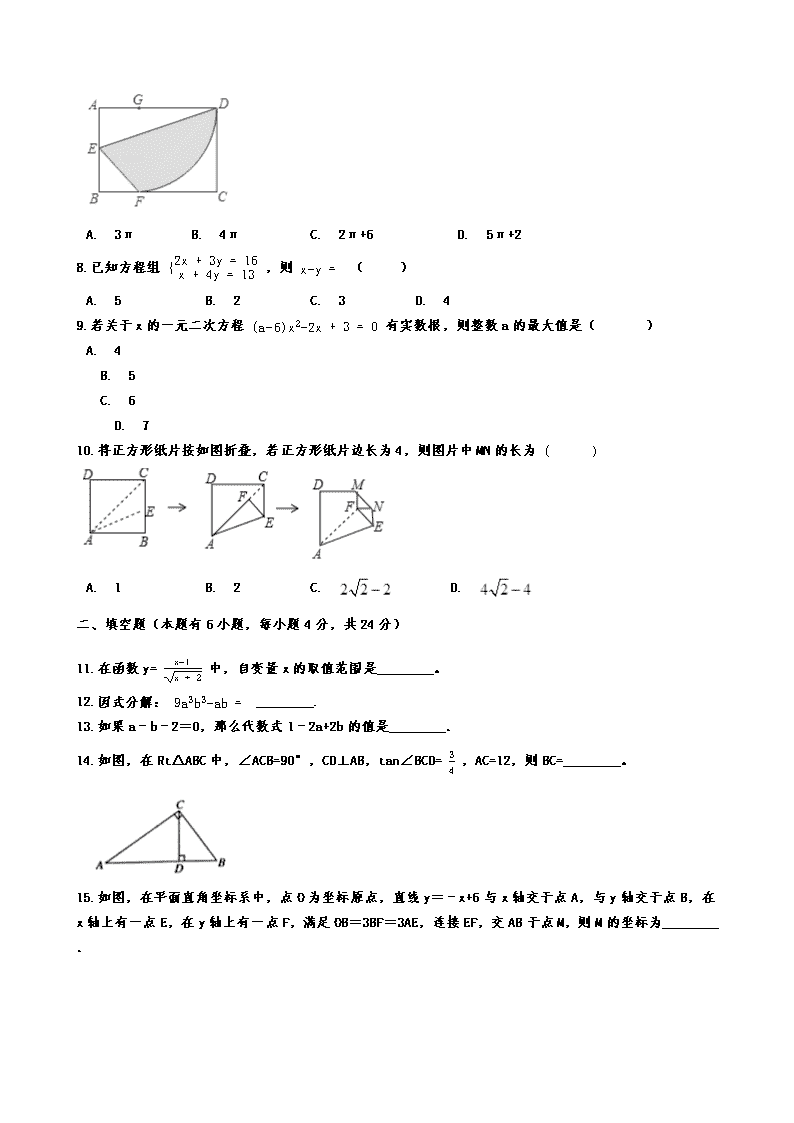
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年浙江省金华、丽水市中考数学押题卷解析版
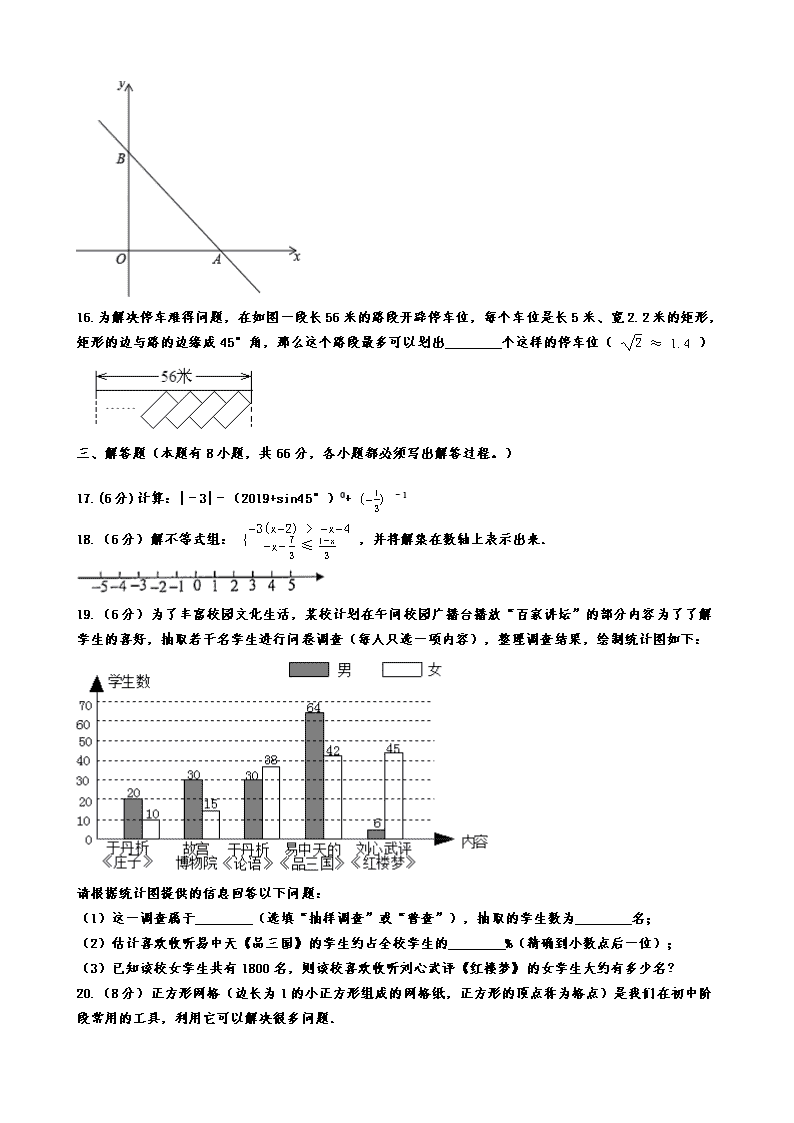
2020年浙江省金华、丽水市中考数学押题卷解析版 一、选择题(本题有10小题,每小题3分,共30分). 1.-12020 的相反数是( ) A. 2020 B. -2020 C. 12020 D. -12020 2.计算(-5a3)²的结果是( ) A. -25a5 B. 25a6 C. 10a6 D. -10a5 3.如图,直线l1∥l2 , 将等边三角形如图放置若∠α=25°,则∠β等于( ) A. 35° B. 30° C. 25° D. 20° 4.从0,1,2,3这四个数中任取一个数记为a,则关于x的不等式 (a−2)x>3(a−2) 的解集为 x<3 的概率是( ) A. 14 B. 13 C. 12 D. 1 5.受新型冠状病毒肺炎影响,学校开学时间延迟,为了保证学生停课不停学,某校开始实施网上教学,张老师统计了本班学生一周网上上课的时间(单位:分钟)如下:200,180,150,200,250.关于这组数据,下列说法正确的是( ) A. 中位数是200 B. 众数是150 C. 平均数是190 D. 方差为0 6.如图,在一单位为1的方格纸上, ΔA1A2A3 , ΔA3A4A5 , ΔA5A6A7 …,都是斜边在 x 轴上,斜边长分别为2,4,6,…的等腰直角三角形,若 ΔA1A2A3 的顶点坐标分别为 A1(2,0) , A2(1,−1) , A3(0,0) ,则依图中所示规律, A2020 的坐标为( ) A. (1010,0) B. (1012,0) C. (2,1012) D. (2,1010) 7.如图,在矩形ABCD中,AB=4,BC=6,点E是AB中点,在AD上取一点G,以点G为圆心,GD的长为半径作圆,该圆与BC边相切于点F,连接DE,EF,则图中阴影部分面积为( ) A. 3π B. 4π C. 2π+6 D. 5π+2 8.已知方程组 {2x+3y=16x+4y=13 ,则 x−y= ( ) A. 5 B. 2 C. 3 D. 4 9.若关于x的一元二次方程 (a−6)x2−2x+3=0 有实数根,则整数a的最大值是( ) A. 4 B. 5 C. 6 D. 7 10.将正方形纸片按如图折叠,若正方形纸片边长为4,则图片中MN的长为 ( ) A. 1 B. 2 C. D. 二、填空题(本题有6小题,每小题4分,共24分) 11.在函数y= x−1x+2 中,自变量x的取值范围是________。 12.因式分解: 9a3b3−ab= ________. 13.如果a﹣b﹣2=0,那么代数式1﹣2a+2b的值是________. 14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,tan∠BCD= 34 ,AC=12,则BC=________。 15.如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+6与x轴交于点A,与y轴交于点B,在x轴上有一点E,在y轴上有一点F,满足OB=3BF=3AE,连接EF,交AB于点M,则M的坐标为________. 16.为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出________个这样的停车位( 2≈1.4 ) 三、解答题(本题有8小题,共66分,各小题都必须写出解答过程。) 17.(6分)计算:|﹣3|﹣(2019+sin45°)0+ (−13) ﹣1 18.(6分)解不等式组: {−3(x−2)>−x−4−x−73≤1−x3 ,并将解集在数轴上表示出来. 19.(6分)为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下: 请根据统计图提供的信息回答以下问题: (1)这一调查属于________(选填“抽样调查”或“普查”),抽取的学生数为________名; (2)估计喜欢收听易中天《品三国》的学生约占全校学生的________%(精确到小数点后一位); (3)已知该校女学生共有1800名,则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名? 20.(8分)正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题. (1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为________; (2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点); (3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值. 21.(8分)如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D. (1)求证:CD是⊙O的切线; (2)E为 弧AB的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= 34 ,BE=BG,EG=3 10 ,求⊙O的半径. 22.(10分)如图,在平面直角坐标系中,双曲线L:y= kx (x>0)过点A(a,b)(0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档