- 2021-05-28 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013成都中考数学试题及答案
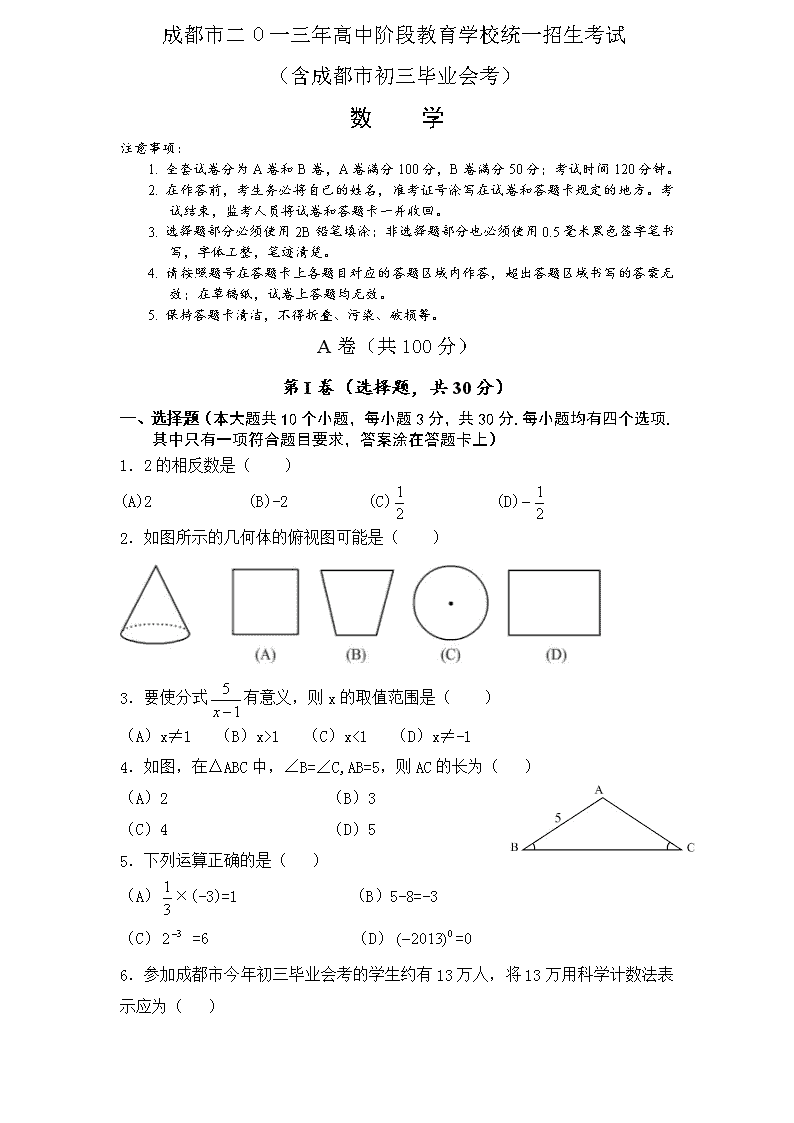
成都市二 O 一三年高中阶段教育学校统一招生考试 (含成都市初三毕业会考) 数 学 注意事项: 1. 全套试卷分为 A 卷和 B 卷,A 卷满分 100 分,B 卷满分 50 分;考试时间 120 分钟。 2. 在作答前,考生务必将自己的姓名,准考证号涂写在试卷和答题卡规定的地方。考 试结束,监考人员将试卷和答题卡一并收回。 3. 选择题部分必须使用 2B 铅笔填涂;非选择题部分也必须使用 0.5 毫米黑色签字笔书 写,字体工整,笔迹清楚。 4. 请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无 效;在草稿纸,试卷上答题均无效。 5. 保持答题卡清洁,不得折叠、污染、破损等。 A 卷(共 100 分) 第 I 卷(选择题,共 30 分) 一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分.每小题均有四个选项. 其中只有一项符合题目要求,答案涂在答题卡上) 1.2 的相反数是( ) (A)2 (B)-2 (C) (D) 2.如图所示的几何体的俯视图可能是( ) 3.要使分式 有意义,则 x 的取值范围是( ) (A)x≠1 (B)x>1 (C)x<1 (D)x≠-1 4.如图,在△ABC 中,∠B=∠C,AB=5,则 AC 的长为( ) (A)2 (B)3 (C)4 (D)5 5.下列运算正确的是( ) (A) ×(-3)=1 (B)5-8=-3 (C) =6 (D) =0 6.参加成都市今年初三毕业会考的学生约有 13 万人,将 13 万用科学计数法表 示应为( ) 2 1 2 1− 1 5 −x 3 1 32− 0)2013(− (A)1.3× (B)13× (C)0.13× (D)0.13× 7.如图,将矩形 ABCD 沿对角线 BD 折叠,使点 C 和点 重合,若 AB=2,则 D 的长为( ) (A)1 (B)2 (C)3 (D)4 8.在平面直角坐标系中,下列函数的图像经过原点的是( ) (A)y=- +3 (B)y= (C)y= (D)y= 9.一元二次方程 x2+x-2=0 的根的情况是( ) (A)有两个不相等的实数根 (B)有两个相等的实数根 (C)只有一个实数根 (D)没有实数根 10.如图,点 A,B,C 在⊙O 上,∠A=50°,则∠BOC 的度数为( ) (A)40° (B)50° (C)80° (D)100° 二.填空题(本大题共 4 个小题,每小题 4 分, 共 16 分,答案写在答题卡上) 11.不等式 的解集为_______________. 12.今年 4 月 20 日在雅安市芦山县发生了 7.0 级 的大地震,全川人民众志成城,抗震救灾,某班组 织“捐零花钱,献爱心”活动,全班 50 名学生的 捐 款 情 况 如 图 所 示 , 则 本 次 捐 款 金 额 的 众 数 是 __________元. 13.如图,∠B=30°,若 AB∥CD,CB 平分∠ACD, 则∠ACD=__________度. 14.如图,某山坡的坡面 AB=200 米,坡角∠BAC=30°, 510 410 510 610 'C 'C x x 5 x2 72 2 −+− xx 312 >−x 则该山坡的高 BC 的长为__________米. 三.解答题(本大题共 6 个小题,共 54 分) 15.(本小题满分 12 分,每题 6 分) (1)计算 (2)解方程组 16.(本小题满分 6 分) 化简 17.(本小题满分 8 分) 如图, 在边长为 1 的小正方形组成的方格纸上,将△ABC 绕着点 A 顺时针旋转 90° (1)画出旋转之后的△ (2)求线段 AC 旋转过程中扫过的扇形的 面积 18.(本小题满分 8 分) “中国梦”关乎每个人的幸福生活, 为进一步感知我们身边的幸福,展现成都人 追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要 求参赛学生每人交一件作品. 现将参赛的 50 件作品的成绩(单位:分)进行统 计如下: 等级 成绩(用 表示) 频数 频率 A 90≤ ≤100 0.08 B 80≤ <90 35 1260sin2|3|)2( 2 −+−+− =− =+ 52 1 yx yx 1 12)( 2 2 − +−÷− a aaaa ''CAB s s x s y C <80 11 0.22 合 计 50 1 请根据上表提供的信息,解答下列问题: (1)表中的 的值为_______, 的值为________ (2)将本次参赛作品获得 等级的学生一次用 , , ,…表示,现该校 决定从本次参赛作品中获得 等级学生中,随机抽取两名学生谈谈他们的参赛体 会,请用树状图或列表法求恰好抽到学生 和 的概率. 19.(本小题满分 10 分) 如图,一次函数 的图像与反比例函数 ( 为常数,且 )的图 像都经过点 (1)求点 的坐标及反比例函数的表达式; (2)结合图像直接比较:当 时, 和 的大小. 20.(本小题满分 10 分) 如图,点 在线段 上,点 , 在 同 侧, , , . (1)求证: ; (2)若 , ,点 为线段 上 的动点,连接 ,作 ,交直线 与点 ; i)当点 与 , 两点不重合时,求 的值; ii)当点 从 点运动到 的中点时,求线段 的中点所经过的路径(线段)长.(直接写出结果, 不必写出解答过程) B 卷(共 50 分) 一、填空题(本大题共 5 个小题,每小题 4 分,共 20 分,答案写在答题卡上) 21. 已知点 在直线 ( 为常数,且 )上,则 的值为 _____. s x y A 1A 2A 3A A 1A 2A 1 1y x= + 2 ky x = k 0≠k )2,(mA A 0>x 1y 2y B AC D E AC 90A C∠ = ∠ = BD BE⊥ AD BC= CEADAC += 3AD = 5CE = P AB DP DPPQ ⊥ BE Q P A B DP PQ P A AC DQ (3,5) y ax b= + ,a b 0a ≠ 5 a b − 22. 若正整数 使得在计算 的过程中,各数位均不产生进位现 象,则称 为“本位数”.例如 2 和 30 是“本位数”,而 5 和 91 不是“本位 数”.现从所有大于 0 且小于 100 的“本位数”中,随机抽取一个数,抽到偶数 的概率为_______. 23. 若关于 的不等式组 ,恰有三个整数解,则关于 的一次函数 的图像与反比例函数 的图像的公共点的个数为_________. 24. 在平面直角坐标系 中,直线 ( 为常数)与抛物线 交 于 , 两点,且 点在 轴左侧, 点的坐标为 ,连接 .有以下 说法:○1 ;○2 当 时, 的值随 的增大而 增大;○3 当 时, ;○4 面积的最小值为 . 其中正确的是_______.(写出所有正确说法的序号) 25. 如图, ,为⊙ 上相邻的三个 等分点, ,点 在弧 上, 为⊙ 的直径,将⊙ 沿 折叠,使点 与 重合,连接 , , .设 , , .先探究 三者的 数量关系:发现当 时, .请继续探究 三 者的数量关系: 当 时, _______;当 时, _______. (参考数据: , ) 二、解答题(本小题共三个小题,共 30 分.答案写在答题卡上) 26.(本小题满分 8 分) n ( 1) ( 2)n n n+ + + + n t 0 2 1 4 t a t − ≥ + ≤ x 1 4y x a= − 3 2ay x += xOy y kx= k 21 23y x= − A B A y P (0, 4)− ,PA PB 2PO PA PB= ⋅ 0k > ( )( )PA AO PB BO+ − k 3 3k = − 2BP BO BA= ⋅ PAB∆ 4 6 A B C, , O n AB BC= E BC EF O O EF A 'A 'EB EC 'EA 'EB b= EC c= 'EA p= , ,b c p 3n = p b c= + , ,b c p 4n = p = 12n = p = 6 2sin15 cos75 4 −= = 6 2cos15 sin 75 4 += = 某物体从 点运动到 点所用时间为 7 秒,其运动速度 (米每秒)关于时间 (秒) 的函数关系如图所示. 某学习小组经过探究发 现:该物体前进 3 秒运动的路程在数值上等于 矩形 的面积. 由物理学知识还可知:该 物体前 ( )秒运动的路程在数值上等 于矩形 的面积与梯形 的面积之和. 根据以上信息,完成下列问题: (1)当 时,用含 的式子表示 ; (2)分别求该物体在 和 时,运动的路程 (米)关于时间 (秒)的函数关系式;并求该物体从 点运动 到 总路程的 时所用的时间. 27.(本小题满分 10 分) 如图,⊙ 的半径 ,四边形 内接圆⊙ , 于点 , 为 延长线上的一点,且 . (1)试判断 与⊙ 的位置关系,并说明理由: (2)若 , ,求 的 长; (3)在(2)的条件下,求四边形 的面积. 28.(本小题满分 12 分) 在平面直角坐标系中,已知抛物线 ( 为常数)的顶点为 , P Q v t AODB n 3 7n< ≤ AODB BDNM 3 7n< ≤ t v 0 3t≤ ≤ 3 7n< ≤ s t P Q 7 10 O 25r = ABCD O AC BD⊥ H P CA PDA ABD∠ = ∠ PD O 3tan 4ADB∠ = 4 3 3 3PA AH −= BD ABCD 21 2y x bx c= − + + ,b c P 等腰直角三角形 的定点 的坐标为 , 的坐标为 ,直角顶点 在第四象限. (1)如图,若该抛物线过 , 两点,求该抛物线的函数表达式; (2)平移(1)中的抛物线,使顶点 在直线 上滑动,且与 交于另一点 . i)若点 在直线 下方,且为平移前(1)中的抛物线上的点,当以 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点 的坐标; ii)取 的中点 ,连接 .试探究 是否存在最大值?若存在,求 出该最大值;若不存在,请说明理由. 成都市二 O 一三年高中阶段教育学校统一招生考试 ABC A (0, 1)− C (4,3) B A B P AC AC Q M AC M P Q、 、 M BC N ,NP BQ PQ NP BQ+ 数学答案 A 卷 1~5:BCADB 6~10: ABCAD 11、 x >2 12、10 13、60° 14、100 15.(1)4; (2) 16. a 17.(1)略 (2) 18.(1)4, 0.7 (2)树状图(或列表)略,P= 19.(1)A(1,2) , (2)当 0查看更多