- 2021-05-28 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
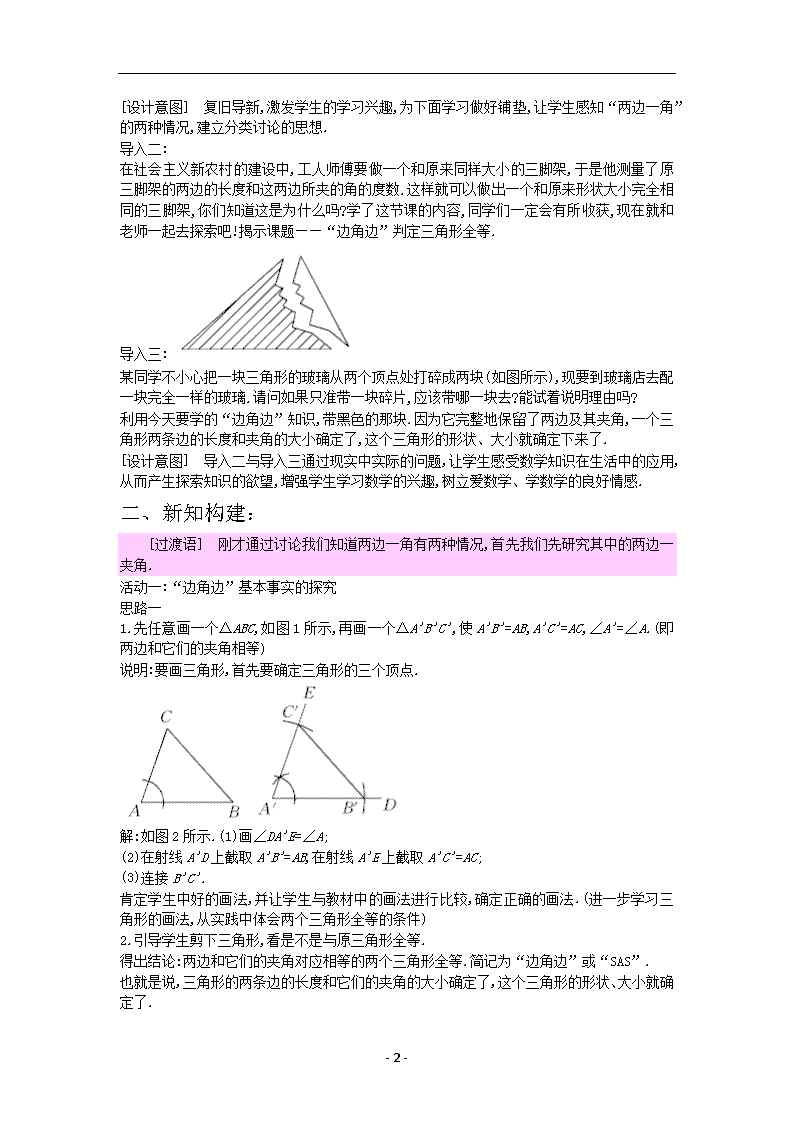
数学冀教版八年级上册教案13-3全等三角形的判定(2)
- 1 - 13.3 全等三角形的判定(2) 教学目标 【知识与能力】 1.掌握“边角边”基本事实的内容. 2.能初步应用“边角边”判定两个三角形全等. 【过程与方法】 1.使学生初步探索三角形全等的过程,体验操作、归纳得出数学结论的过程. 2.体会利用转化的数学思想和方法解决问题的过程. 【情感态度价值观】 通过探究三角形全等的基本事实的活动,培养学生观察分析图形的能力及运算能力,培养学 生乐于探索的良好品质以及发现问题的能力. 教学重难点 【教学重点】 “边角边”基本事实的理解和应用. 【教学难点】 指导学生分析问题,寻找判定三角形全等的条件. 课前准备 多媒体课件 教学过程 一、新课导入: 导入一: 【提出问题】 【课件 1】 1.怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(SSS)的内 容是什么? 2.如果两个三角形有两条边和一个角分别对应相等,这两个三角形一定全等吗?此时应该有 两种情况,一种是角夹在两条边的中间,形成两边一夹角,一种是角不夹在两边的中间,形成 两边一对角,如图所示: - 2 - [设计意图] 复旧导新,激发学生的学习兴趣,为下面学习做好铺垫,让学生感知“两边一角” 的两种情况,建立分类讨论的思想. 导入二: 在社会主义新农村的建设中,工人师傅要做一个和原来同样大小的三脚架,于是他测量了原 三脚架的两边的长度和这两边所夹的角的度数.这样就可以做出一个和原来形状大小完全相 同的三脚架,你们知道这是为什么吗?学了这节课的内容,同学们一定会有所收获,现在就和 老师一起去探索吧!揭示课题——“边角边”判定三角形全等. 导入三: 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图所示),现要到玻璃店去配 一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去?能试着说明理由吗? 利用今天要学的“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三 角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了. [设计意图] 导入二与导入三通过现实中实际的问题,让学生感受数学知识在生活中的应用, 从而产生探索知识的欲望,增强学生学习数学的兴趣,树立爱数学、学数学的良好情感. 二、新知构建: [过渡语] 刚才通过讨论我们知道两边一角有两种情况,首先我们先研究其中的两边一 夹角. 活动一:“边角边”基本事实的探究 思路一 1.先任意画一个ΔABC,如图 1 所示,再画一个ΔA'B'C',使 A'B'=AB,A'C'=AC,∠A'=∠A.(即 两边和它们的夹角相等) 说明:要画三角形,首先要确定三角形的三个顶点. 解:如图 2 所示.(1)画∠DA'E=∠A; (2)在射线 A'D 上截取 A'B'=AB,在射线 A'E 上截取 A'C'=AC; (3)连接 B'C'. 肯定学生中好的画法,并让学生与教材中的画法进行比较,确定正确的画法.(进一步学习三 角形的画法,从实践中体会两个三角形全等的条件) 2.引导学生剪下三角形,看是不是与原三角形全等. 得出结论:两边和它们的夹角对应相等的两个三角形全等.简记为“边角边”或“SAS”. 也就是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确 定了. - 3 - 用符号语言表述为: 在ΔABC 与ΔA'B'C'中, �ㄱ = � ' ㄱ ', ∠ � = ∠ � ', �� = � ' � ', ∴ΔABC≌ΔA'B'C'(SAS). [知识拓展] “SAS”中的“A”必须是两个“S”所夹的角. 3.【课件 2】 问题:如果把“两边及其夹角分别相等”改为“两边及其中一边的对角相等”, 那么这两个三角形还全等吗? 根据学生的讨论,教师应该及时点拨,必要时可以画反例图形. 通过反例证明:已知两边及其中一边的对角分别相等的两个三角形全等不一定成立.(让学生 了解推翻一个结论可以通过举反例) 思路二 1.引导学生画一个三角形,使它的两条边分别是 1.5 cm,2.5 cm,并且使长为 1.5 cm 的这条 边所对的角是 30°.(小组交流后比较画出的图形是否全等,小组内选代表发言) 【课件 3】 如图所示,把一长一短的两根木棍的一端固定在一起,摆出ΔABC,固定住长木 棍,转动短木棍,得到ΔABD.这个试验说明了什么? 教师让学生观察运动过程,并加以分析.指出:两个三角形的两条边和其中一条边的对角分别 相等时,这两个三角形不一定全等. 2.画一个ΔABC,使 AB=3 cm,BC=4 cm,∠B=60°.比较小组内成员所画的三角形是否全等. 出示教材第 41 页“一起探究”和观察与思考. (让学生动手操作,提高学生的动手能力和小组合作学习的能力,从而让学生发现“边角边” 定理) 【提出问题】 通过刚才的操作,你能得出什么结论? 学生交流后得出基本事实:即“如果两个三角形的两边和它们的夹角对应相等,那么这两个三 角形全等”. 简记为“边角边”或“SAS”. 出示教材第 42 页“大家谈谈”,说明全等三角形的性质在生活中的广泛应用.在判定两个三 角形全等时,经常要用到对顶角、公共角或公共边. 活动二:例题讲解 [过渡语] 根据“SAS”我们可以判定两个三角形全等,在判定的时候要先确定相等的两 组边和这两条边所夹的角. 【课件 4】 已知:如图所示,AD∥BC,AD=CB.求证:ΔADC≌ΔCBA. - 4 - 〔解析〕 根据两直线平行,内错角相等得到∠1=∠2.再根据“SAS”进行判定,注意 AC 是两 个三角形的公共边. 学生写出推理过程,教师找一名学生到黑板板演,然后教师讲评) 【课件 5】 (补充例题)如图所示,为了测量出池塘两端 A,B 两点之间的距离,在地面上找到一点 C,连接 BC,AC,使∠ACB=90°,然后在 BC 的延长线上确定 D,使 CD=BC,那么只要测量出 AD 的 长度也就得到了 A,B 两点之间的距离.你能说明其中的道理吗? 教师引导学生把实际问题转化为数学问题,观察图形中有没有全等的三角形,如果要证全等 三角形,还需要哪些条件? 〔解析〕 此题只需说明ΔABC≌ΔADC 即可,这两个三角形都是直角三角形,而且夹直角的 两边对应相等. 想一想:在题目中哪两个角相等?依据的是什么? 解:因为∠ACB=90°, 所以∠ACD=180°-∠ACB=90°. 又因为 BC=DC,AC=AC, 所以ΔABC≌ΔADC(SAS), 所以 AB=AD(全等三角形的对应边相等). 小结:从例 2 可以看出:因为全等三角形的对应边相等、对应角相等,所以证明线段相等或角 相等时,可以通过证明它们是全等三角形的对应边或对应角来解决. [知识拓展] 在利用“SAS”判定两个三角形全等时,要注意这个角是不是两个三角形的公共 角、对顶角. 巩固练习: 如 图 所 示 , 根 据 题 目 条 件 , 判 断 每 组 中 的 三 角 形 是 否 全 等 . (1)在图(1)中,AC=DF,∠C=∠F,BC=EF; (2)BC=BD,∠ABC=∠ABD. - 5 - 解:(1)全等. (2)全等. [设计意图] 通过例题和练习使学生掌握用“边角边”判定两个三角形全等的方法. 三、课堂小结: 两边及其夹角对应相等的两个三角形全等,简记为“边角边”或“SAS”. 注意:三角形全等的基本事实“SAS”中的相等的角必须是夹角,否则这两个三角形不一定全 等,即有两边和其中一边的对角对应相等的两个三角形不一定全等.查看更多