五年级下册数学教案－智慧广场-鸡兔同笼 ｜青岛版（五四学制） (2)

五年级下册数学教案－智慧广场-鸡兔同笼 ｜青岛版（五四学制） (2)

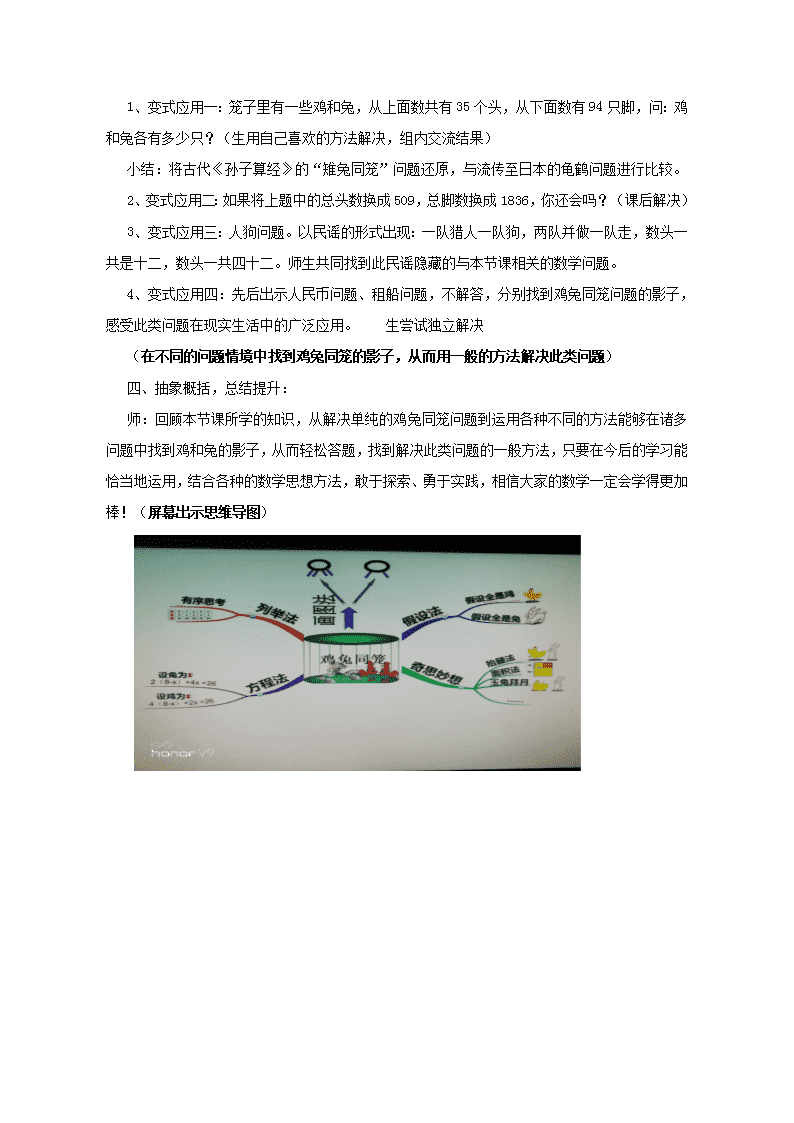
《智慧广场——鸡兔同笼》教学设计 教学目标： 1、初步认识鸡兔同笼的数学趣题，了解有关的数学史。能用列表法和画图法解决相关的实 际问题，结合图解法理解假设的方法解决鸡兔同笼问题。 2、通过列表举例、画图分析、假设计算等方法理解数量关系，体会数形结合的方便性，体 验解决问题方法的多样化，提高解决实际问题的能力。 3、培养学生的合作意识，提高学生解决问题的能力和自信心，受到多种数学思想方法的熏 陶，进而让学生体会数学的价值。 教学重难点： 1、掌握用假设法解决鸡兔同笼问题，找到解决鸡兔同笼问题的一般方法。 2、理解用假设法解决鸡兔同笼问题的算理。 教具学具： 多媒体课件、实物展台 教学过程： 一、创设情境 揭示课题 师：今天老师给大家带来两个谜语，一起猜猜看吧！ 耳朵长、尾巴短，爱吃萝卜爱吃菜，蹦蹦跳跳真可爱。（猜一动物） 顶上红冠戴，身披五彩衣，能测天亮时，呼得众人醒。（打一动物） 师揭示课题：这节课我们就一起来研究将这样的一群动物关在一个笼子里的数学问题。 板书课题：鸡兔同笼。 二、合作探究 获取新知 （大屏幕出示：笼子里有一些鸡和兔，从面数有 8 个头，问：鸡和兔各有多少只？） 1、据信息猜测笼子里鸡兔各有几只？（引导学生有序列举） 师：从上表中能发现什么？ 师：刚才这些可能的情况仅是我们的猜想，那鸡和兔分别各有多少只呢？ 2、借助探究单一，用列举法验证猜想：鸡和兔分别有几只？屏幕出示：共有 26 条腿 3、活动预设： ①逐一列举：按着一定的顺序一种种的列举，直到找到正确答案；（小结表格中的规 律：鸡和兔的只数变化引起腿的只数变化，兔子每多一只鸡每少一只，腿的总数多 2 只） ②取中列举：先出现 4 只和 4 只，发现腿的只数还不够，所以让兔子增加鸡减少； ③跳跃列举： 4、小结：①有序列举可以帮助我们做到不重复不遗漏地找到所有可能情况； ②总只数不变的情况下根据腿的总数调整鸡和兔的只数； ③列举时可以逐一列举、取中列举和跳跃列举，据情况选择。 5、设疑：刚才同学们学会了用列举法解决类似的鸡兔同笼问题，接下来我把题目改一下， 看大家还会吗？师口述：笼子里有一些鸡和兔，从上面数共有 509 个头，从下面数有 1836 只脚， 问：鸡和兔各有多少只？（产生冲突：刚才的列举法不能解决数字较大的问题，需要找到更好 的更一般的解决类似问题的方法。） 6、小组合作探究：找一般的解决鸡兔同笼问题的方法。 7、指名用画图法完成的学生将图画在黑板上。 8、指名学生将假设法写到黑板上。（假设全是鸡或兔都可以） 假设全是鸡：2×8=16（条） 少了：26－16=10（条） 兔：10÷2=5（只） 鸡：8－5=3（只） 9、总结：（1）、画图法，可以全是鸡，也可以全画成兔，习惯上是画少了再添。（2）、 假设法，预设三种疑问情况（为什么假设全是鸡的情况下先求出的是兔的只数？为什么求兔的只 数要除以 2？为什么我们假设全是鸡或全是兔？） （渗透方程思想） 三、巩固应用，内化提高 1、变式应用一：笼子里有一些鸡和兔，从上面数共有 35 个头，从下面数有 94 只脚，问：鸡 和兔各有多少只？（生用自己喜欢的方法解决，组内交流结果） 小结：将古代《孙子算经》的“雉兔同笼”问题还原，与流传至日本的龟鹤问题进行比较。 2、变式应用二：如果将上题中的总头数换成 509，总脚数换成 1836，你还会吗？（课后解决） 3、变式应用三：人狗问题。以民谣的形式出现：一队猎人一队狗，两队并做一队走，数头一 共是十二，数头一共四十二。师生共同找到此民谣隐藏的与本节课相关的数学问题。 4、变式应用四：先后出示人民币问题、租船问题，不解答，分别找到鸡兔同笼问题的影子， 感受此类问题在现实生活中的广泛应用。 生尝试独立解决 （在不同的问题情境中找到鸡兔同笼的影子，从而用一般的方法解决此类问题） 四、抽象概括，总结提升： 师：回顾本节课所学的知识，从解决单纯的鸡兔同笼问题到运用各种不同的方法能够在诸多 问题中找到鸡和兔的影子，从而轻松答题，找到解决此类问题的一般方法，只要在今后的学习能 恰当地运用，结合各种的数学思想方法，敢于探索、勇于实践，相信大家的数学一定会学得更加 棒！（屏幕出示思维导图）