- 2021-05-28 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学九年级下册课件-第26章 二次函数-26二次函数的图象与性质
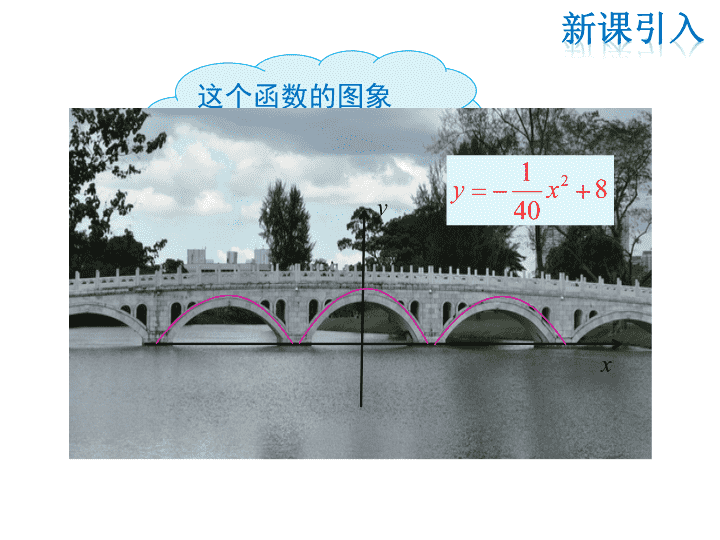
HS九(下) 教学课件 26.2 二次函数的图象与性质 第1课时 二次函数y=ax2+k的图象与性质 2.二次函数y=ax2+bx+c的图象与性质 已知二次函数 ① y=-x2; ② y= x2; ③ y=15x2; ④ y=-4x2; ⑤ y= - x2; ⑥ y=4x2. (1)其中开口向上的有 (填题号); (2)其中开口向下,且开口最大的是 (填题号); (3)当自变量由小到大变化时,函数值先逐渐变大,然后 逐渐变小的有 (填题号). 3 5 9 10 ②③⑥ ⑤ ①④⑤ 这个函数的图象 是如何画出来的? x y 21 840y x 解:先列表. x ··· -3 -2 -1 0 1 2 3 ··· ··· ··· ··· ··· 在同一直角坐标系中,画出二次函数 与 的图象. 21 2y x 21 12y x 21 2y x 21 12y x 9 2 11 2 2 1 2 0 1 2 2 9 2 3 3 2 1 3 2 3 11 2 二次函数y=ax2+k的图象与性质1 例1 x y -4 -3 -2 -1 o 1 2 3 4 1 2 3 4 5 6 21 2y x 21 12y x 描点、连线,画出这两个函数的图象 抛物线 , 的开口方向、对称轴和顶点各 是什么? 21 2y x 21 12y x 21 2y x 21 12y x 二次函数 开口方向 顶点坐标 对称轴 向上 向上 (0,0) (0,1) y轴 y轴 想一想:通过上述例子,函数y=ax2+k的性质是什么? 观察与思考 y -2 -2 4 2 2 -4 x0 二次函数y=ax2+k的图象和性质(a<0) 在同一坐标系内画出 下列二次函数的图象: 2 21 3y x 2 2 1 23y x 2 1 1 3 2y x 21 3y x 2 2 1 23y x 2 1 1 3 2y x 根据图象回答下列问题: (1)图象的形状都 是 . (2)三条抛物线的开口方 向_______; (3)对称轴都是 __________; 抛物线 向下 直线x=0 y -2 -2 2 2 -4 x0 2 2 1 23y x 21 3y x 2 1 1 3 2y x (4)从上而下顶点坐标分别是 _____________________; (5)顶点都是最____点,函数都有 最____值,从上而下最大值分 别为_______、_______﹑______; (6)函数的增减性都相同: ____________________________, ____________________________. ( 0,0)( 0,2) ( 0,-2) 高 大 y=0 y= -2y=2 对称轴左侧y随x增大而增大 对称轴右侧y随x增大而减小 -2 -2 2 2 -4 x0 2 2 1 23y x 21 3y x 2 1 1 3 2y x y 二次函数y=ax2+k(a ≠ 0)的性质 y=ax2+k a>0 a<0 开口方向 向上 向下 对称轴 y轴 y轴 顶点坐标 (0,k) (0,k) 最值 当x=0时,y最小值=k 当x=0时,y最大值=k 增减性 当x<0时,y随x的增大 而减小;x>0时,y随x 的增大而增大. 当x>0时,y随x的增大 而减小;x<0时,y随x 的增大而增大. 已知二次函数y=ax2+c,当x取x1,x2(x1≠x2)时, 函数值相等,则当x=x1+x2时,其函数值为________. 解析:由二次函数y=ax2+c图象的性质可知,x1,x2 关于y轴对称,即x1+x2=0.把x=0代入二次函数表达 式求出纵坐标为c. c 方法总结: 二次函数y=ax2+c的图象关于y轴对称, 因此左右两部分折叠可以重合,函数值相等的两点的 对应横坐标互为相反数. 例2 做一做:在同一直角坐标系中,画出二函数y=2x2+1与 y=2x2-1的图象. 解:列表如下. x ··· -2 -1.5 -1 0 1 1.5 2 ··· y =2 x2+1 ··· ··· y = 2x2-1 ··· ··· 9 5.5 3 1 3 5.5 9 7 3.5 1 -1 1 3.5 7 二次函数y=ax2+c的图象及平移3 4-2 2 2 4 6 -4 8 10 -2 y = 2x2+1 y = 2x2-1 (1)抛物线y=2x2+1,y=2x2-1的开口 方向、对称轴和顶点各是什么? y =2 x2 向上 (0,0) y轴 y =2 x2+1 y = 2x2-1 二次函数 开口方向 顶点坐标 对称轴 向上 向上 (0,1) (0,-1) y轴 y轴 4-2 2 2 4 6 -4 8 10 -2 y = 2x2+1 y = 2x2-1 (2) 抛物线 y=2x2+1,y=2x2-1与抛物 线y=2x2 有什么关系? 可以发现,把抛物线y=2x2 向 平移1个单位长 度,就得到抛物线 ;把抛物线 y=2x2 向 平 移1个单位长度,就得到抛物线 y=2x2-1. 下y=2x2+1 上 解析式 y=2x2 2x2+1 y=2x2+1y=2x2-1 +1-1 点的坐标 函数对应值表 x … … y=2x2-1 … … y=2x2 … … y=2x2+1 … … 4.5 -1.5 3.5 5.5 -1 2 1 3 x 2x2 2x2-1 (x, ) (x, ) (x, )2x2-1 2x2 2x2+1 从数的角度探究 二次函数y=ax2+k的图象及平移4 可以看出,y=2x2 向___ 平移一个单位长度得到 抛物线y=2x2+1 5 3 2 1 -6 -4 -2 2 4 6 12 2 xy 22xy 4 o -1 122 xy 可以看出,y=2x2 向___ 平移一个单位长度 得到抛物线y=2x2-1 x y从 形 的 角 度 探 究 上 下 二次函数y=ax2+c的图象可以由 y=ax2 的图象平移 得到: 当c > 0 时,向上平移c个单位长度得到. 当c < 0 时,向下平移-c个单位长度得到. 二次函数y=ax2 与y=ax2+c(a ≠ 0)的图象的关系 u上下平移规律: 平方项不变,常数项上加下减. 二次函数y=-3x2+1的图象是将( ) A.抛物线y=-3x2向左平移3个单位得到 B.抛物线y=-3x2向左平移1个单位得到 C.抛物线y=3x2向上平移1个单位得到 D.抛物线y=-3x2向上平移1个单位得到 解析:二次函数y=-3x2+1的图象是将抛物线 y=-3x2向上平移1个单位得到的.故选D. D 想一想 1.画抛物线y=ax2+c的图象有几步? 第一种方法:平移法,两步即第一步画y=ax2的图 象,再向上(或向下)平移︱c ︱单位. 第二种方法:描点法,三步即列表、描点和连线. a决定开口方向和大小;c决定顶点的纵坐标. 如图,抛物线y=x2-4与x轴交于A、B两点,点 P为抛物线上一点,且S△PAB=4,求P点的坐标. 解:抛物线y=x2-4,令y=0,得到x=2或-2, 即A点的坐标为(-2,0),B点的坐标为(2,0), ∴AB=4. ∵S△PAB=4,设P点纵坐标为b, ∴ ×4|b|=4,∴|b|=2,即b=2或-2. 当b=2时,x2-4=2,解得x=± , 此时P点坐标为( ,2),(- ,2); 当b=-2时,x2-4=-2,解得x=± , 此时P点坐标为( ,2),(- ,2). 1 2 6 6 6 2 2 2 例3 1、抛物线y=2x2向下平移4个单位,就得到抛 物线 . 2、填表: y = 2x2-4 函数 开口方向 顶点 对称轴 有最高(低)点 y = 3x2 y = 3x2+1 y = -4x2-5 向上 向上 向下 (0,0) (0,1) (0,-5) y轴 y轴 y轴 有最低点 有最低点 有最高点 3.已知(m,n)在y=ax2+a(a不为0)的图象上,(-m,n) ___(填“在”或“不在”)y=ax2+a(a不为0)的图 象上. 4. 若y=x2+(k-2)的顶点是原点,则k____;若顶点 位于x轴上方,则k____;若顶点位于x轴下方,则 k . 在 =2 >2 <2 5.不画函数y=-x2和y=-x2+1的图象回答下面的问题: (1)抛物线y=-x2+1经过怎样的平移才能得到抛物线 y=-x2. (2)函数y=-x2+1,当x 时, y随x的增大而减小; 当x 时,函数y有最大值,最大值y是 , 其图象与y轴的交点坐标是 ,与x轴的交点 坐标是 . (3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐 标. 向下平移1个单位. >0 =0 1 (0,1) (-1,0),(1,0) 开口方向向上,对称轴是y轴,顶点坐标(0,-3). 6.对于二次函数y=(m+1)xm2-m+3,当x>0时y随x的增大而 增大,则m=____. 7.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则 a=____. 8.抛物线y=ax2+c与x轴交于A(-2,0)﹑B两点,与y轴 交于点C(0,-4),则三角形ABC的面积是_______. 2 -2 8 9.二次函数y=ax2+c与一次函数y=ax+c的图象在同一坐 标系中的是 ( )B x y 0 x y 0x y 0 x y 0 A B C D 二次函数y=ax2+k(a≠0)的图象和性质 图 象 性 质 与y=ax2的关系 1.开口方向由a的符 号决定; 2.k决定顶点位置; 3.对称轴是y轴. 增减性结合 开口方向和 对称轴才能 确定. 平移规律: k正向上; k负向下.查看更多