- 2021-05-28 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年黑龙江省黑河市中考数学一模试卷(含解析)
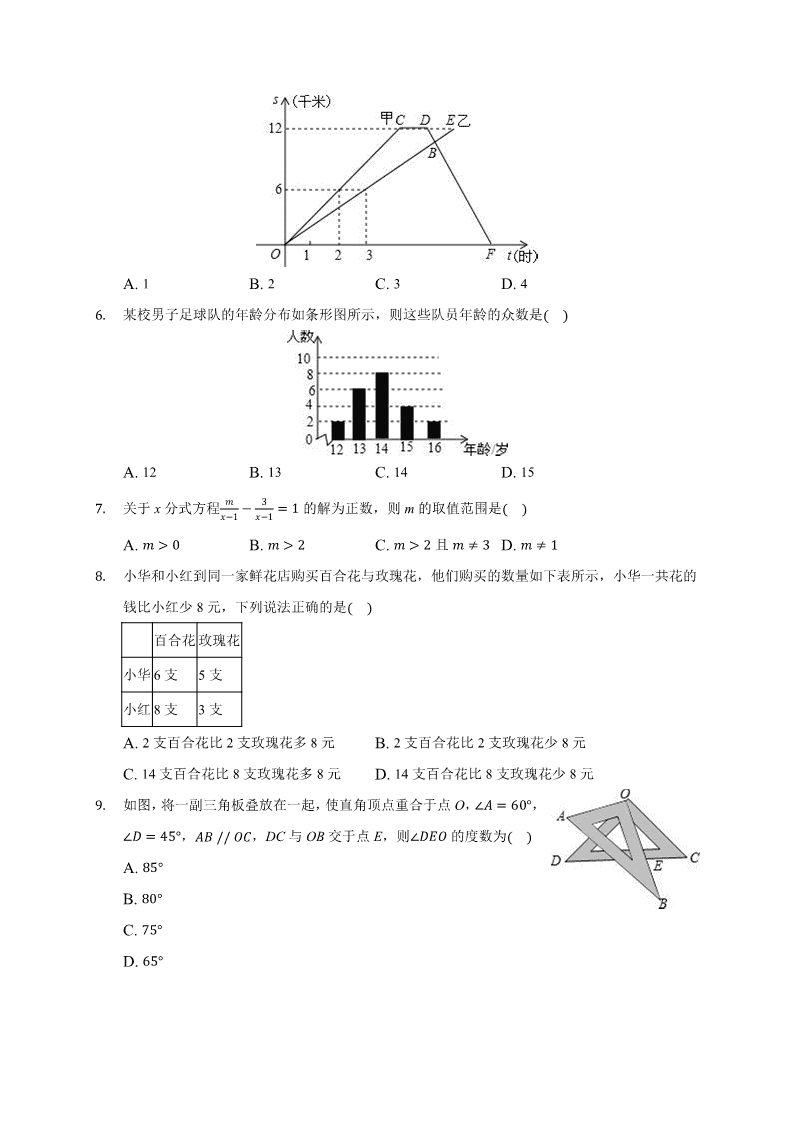
2020 年黑龙江省黑河市中考数学一模试卷 一、选择题(本大题共 10 小题,共 30.0 分) 1. � � 的倒数是 ������A. 1 � B. � 1 � C. 9 D. � � 2. 下面汽车标志中,属于轴对称图形的是 ������ A. B. C. D. 3. 下列计算正确的是 ������A. � � 2� 3 �� 3 �� 䁕� � � 3 B. �2� � �� 2 � �� 2 � � 2 C. 3� 2 � � 2 � �� �� D. � � 2� 3 �� � � 2 �� 2�� �. 一枚质地均匀的正方体骰子,其六个面上分别刻有 1、2、3、4、5、6 的点数,掷这个骰子一次, 则掷得面朝上的点数为偶数的概率是 ������A. 1 䁕 B. 1 � C. 1 3 D. 1 2 5. 甲、乙两名同学进行登山比赛,甲同学和乙同学沿相同的路线同时在早 8:00 从山脚出发前往 山顶,甲同学到达山顶后休息 1 小时,沿原路以每小时 6 千米的速度下山,在这一过程中,各 自行进的路程随所用时间变化的图象如图所示,根据提供信息得出以下四个结论: � 甲同学从山脚到达山顶的路程为 12 千米; � 乙同学登山共用 4 小时; � 甲同学在 14:00 返回山脚; � 甲同学返回与乙同学相遇时,乙同学距登到山顶还有 1.� 千米的路程. 以上四个结论正确的有 ������ 个 A. 1 B. 2 C. 3 D. 4 䁕. 某校男子足球队的年龄分布如条形图所示,则这些队员年龄的众数是 ������ A. 12 B. 13 C. 14 D. 15 7. 关于 x 分式方程 � ��1 � 3 ��1 � 1 的解为正数,则 m 的取值范围是 ������A. � 香 䁥 B. � 香 2 C. � 香 2 且 � � 3 D. � � 1 8. 小华和小红到同一家鲜花店购买百合花与玫瑰花,他们购买的数量如下表所示,小华一共花的 钱比小红少 8 元,下列说法正确的是 ������百合花 玫瑰花 小华 6 支 5 支 小红 8 支 3 支 A. 2 支百合花比 2 支玫瑰花多 8 元 B. 2 支百合花比 2 支玫瑰花少 8 元 C. 14 支百合花比 8 支玫瑰花多 8 元 D. 14 支百合花比 8 支玫瑰花少 8 元 �. 如图,将一副三角板叠放在一起,使直角顶点重合于点 O, �� � 䁕䁥� , �� � �5� , �������� ,DC 与 OB 交于点 E,则 ��ᦙ� 的度数为 ������A. 85�B. 8䁥�C. 75�D. 䁕5� 1䁥. 如图,二次函数 � � �� 2 � �� � � 的图象与 x 轴交于 A 点,抛物线的对称轴是直线 � �� 1 ,以 下结论: ���� 香 䁥 , �� � 2� � 䁥 , �� 2 � ��� 香 䁥 , ��� � 2� � � ܾ 䁥 ,正确的有 ������ A. �� B. �� C. �� D. ��二、填空题(本大题共 7 小题,共 21.0 分) 11. 中国的领水面积约为 37䁥䁥䁥䁥䁥Ͳ� 2 ,将 3700000 用科学记数法表示为______. 12. 在函数 � � 1 � � � 2 中,自变量 x 的取值范围是_______________. 13. 如图,已知 �� � �ᦙ , ���� � ���ᦙ ,要使 � ���≌� �ᦙ� ,还 需添加一个条件,这个条件可以是______ . 1�. 图是一个几何体的三视图,这个几何体是 ,它的侧面积是 � 结果不取近似值 � . 15. 等腰三角形一边长是 8,另一边长是 4,则周长是________ 1䁕. 如图,矩形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上,点 O 与坐标原 点重合,B 点坐标是 ���2� ,反比例函数 � � Ͳ � 的图象经过对角线 OB、 AC 的交点 M,则 k 的值是______. 17. 如图所示,在平面直角坐标系中,直线 l 交 x 轴于点 �� � 2�䁥� ,交 y 轴于点 �1�䁥�2� ,点 �2 , �3 , � 在直线 l 上,点 �1 , �2 , �3 , � 在 x 轴的正半轴上.若 � �1��1 , � �2�1�2 , � �3�2�3 , � 依次均为 等腰直角三角形,直角顶点都在 x 轴上,则第 n 个等腰直角三角形 �����1�� 的顶点 �� 的横坐标为__________. 三、解答题(本大题共 7 小题,共 69.0 分) 18. 计算: � � 1� � � � �1 � 2� 䁥 � ��ݏ�3䁥� . 1�. 解方程: � 2 � �� � 5 � 䁥 . 2䁥. � ��� 中, �� � �� � 1䁥 , �� � 12 , � � 是 � ��� 的外接圆. �1� 如图 � ,过 A 作 �ൌ���� ,求证:MN 与 � � 相切; �2� 如图 � , ���� 的平分线交半径 OA 于点 E,交 � � 于点 �. 求 � � 的半径和 AE 的长. 21. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本 校部分学生进行调查,并绘制成部分统计图表如下: 类别 家庭藏书 m 本 学生人数 A 䁥 � � � 25 20 B 2䁕 � � � 1䁥䁥 a C 1䁥1 � � � 2䁥䁥 50 D � � 2䁥1 66 根据以上信息,解答下列问题: �1� 该调查的样本容量为______, � � ______; �2� 在扇形统计图中,“A”对应扇形的圆心角为______ � ; �3� 若该校有 2000 名学生,请估计全校学生中家庭藏书 200 本以上的人数. 22. 甲、乙两辆汽车沿同一路线从 A 地前往 B 地,甲以 a 千米 � 时的速度匀速行驶,途中出现故障 后停车维修,修好后以 2a 千米 � 时的速度继续行驶;乙在甲出发 2 小时后匀速前往 B 地,设甲、 乙两车与 A 地的路程为 �� 千米 � ,甲车离开 A 地的时间为 �� 时 � ,s 与 t 之间的函数图象如图所示. �1� 求 a 和 b 的值. �2� 求两车在途中相遇时 t 的值. �3� 当两车相距 60 千米时, � � ______时. 23. 如图,将矩形纸片 ABCD 沿对角线 AC 折叠,使点 B 落到点 �� 的位置, ��� 与 CD 交于点 E,且 �� � 8 , �� � � . �1� 求证: � ��ᦙ≌� ���ᦙ ; �2� 求 DE 的长; �3�戀 为线段 AC 上的任意一点, 戀� � �ᦙ 于 G, 戀� � ᦙ� 于 H, 则 戀� � 戀� 的值 � ______. 24. 如图,抛物线 � � �� 2 � �� � � 与 x 轴交于点 �� � 2�䁥� 和点 ����䁥�.点 C 是抛物线第一象限上一点, �� � � 轴于 �. 点 D 是 BC 的中点, DH 与 y 轴交于点 E. �1� 求抛物线的解析式. �2� 当 C 恰好是抛物线的顶点时,求点 E 的坐标. �3� 当 � ��� 的面积是 � ᦙ�� 面积的 3 2 时,求 tan���� 的值. 【答案与解析】 1.答案:B 解析: 本题考查倒数的知识 . 根据倒数的定义即可解答. 解: � � 的倒数 � 1 � . 故选 B. 2.答案:C 解析:解:A、不是轴对称图形,故本选项错误; B、不是轴对称图形,故本选项错误; C、是轴对称图形,故本选项正确; D、不是轴对称图形,故本选项错误. 故选 C. 根据轴对称图形的概念对各选项分析判断即可得解. 本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合. 3.答案:D 解析:解: �.� � 2� 3 �� 3 �� 8� � � 3 ,此选项错误; B. �2� � �� 2 � �� 2 � ��� � � 2 ,此选项错误; C. 3� 2 � � 2 � �� 2 ,此选项错误; D. � � 2� 3 �� � � 2 �� 2�� ,此选项正确; 故选:D. 分别根据单项式的乘方、完全平方公式和合并同类项法则及单项式的除法计算可得. 本题主要考查整式的混合运算,解题的关键是掌握整式的混合运算顺序和运算法则. 4.答案:D 解析:解: � 在 1、2、3、4、5、6 这 6 个数中,偶数有 2、4、6 这 3 个, � 掷得面朝上的点数为偶数的概率是 3 䁕 � 1 2 , 故选:D. 先统计出偶数点的个数,再根据概率公式解答. 此题主要考查了概率公式,用到的知识点为:概率 � 所求情况数与总情况数之比. 5.答案:A 解析: 本题考查了函数图象以及解一元一次方程,观察函数图象逐一分析四条结论的正误是解题的关键. � 由 s 的最大值为 12,可得出甲同学从山脚到达山顶的路程为 12 千米,结论 � 正确; � 利用速度 � 路程 � 时间可求出乙登山的速度,由时间 � 路程 � 速度可求出乙登山用的时间,结论 � 错误; � 利 用速度 � 路程 � 时间可求出甲登山的速度,由时间 � 路程 � 速度可求出甲登山及下山所用时间,再结 合甲的出发时间及中间休息一小时,可得出甲同学在 15:00 返回山脚,结论 � 错误; � 设二者相 遇所用时间为 x,根据路程 � 甲下山的路程 � 乙上山的路程,即可得出关于 x 的一元一次方程,解之 即可得出 x 的值,再根据离山顶的距离 � 山顶到山脚的路程 � 乙登山的路程,即可得出二人相遇时, 乙同学距山顶的路程为 1.5 千米,结论 � 错误.综上即可得出结论. 解: � � � 值的最大值为 12, � 甲同学从山脚到达山顶的路程为 12 千米,结论 � 正确; � 乙同学登山的速度为 䁕 � 3 � 2� 千米 � 时 � , 乙同学登山所用时间为 12 � 2 � 䁕� 小时 � , � 乙同学登山共用 6 小时,结论 � 错误; � 甲同学登山的速度为 䁕 � 2 � 3� 千米 � 时 � , 甲同学登山所用时间为 12 � 3 � �� 小时 � , 甲同学下山所用时间为 12 � 䁕 � 2� 小时 � , � 甲同学返回山脚的时间为 8 � � � 1 � 2 � 15 时,结论 � 错误; � 设二者相遇所用时间为 x, 根据题意得: 䁕�� � � � 1� � 2� � 12 , 解得: � � 5.25 , � 二人相遇时,乙同学距山顶的距离为 12 � 2 � 5.25 � 1.5� 千米 � , � 结论 � 错误. 综上所述:正确的结论有 � . 故选:A. 6.答案:C 解析:解:观察条形统计图知:14 岁的人数最多,有 8 人, 故众数为 14 岁, 故选 C. 根据条形统计图找到最高的条形图所表示的年龄数即为众数. 本题考查了众数的定义及条形统计图的知识,解题的关键是能够读懂条形统计图及了解众数的定义, 难度较小. 7.答案:C 解析: 此题考查了分式方程的解,需注意在任何时候都要考虑分母不为 䁥. 分式方程去分母转化为整式方程, 求出整式方程的解表示出 x,由解为正数求出 m 的范围即可. 解:去分母得: � � 3 � � � 1 , 解得: � � � � 2 , 由分式方程的解为正数,得到 � � 2 香 䁥 ,且 � � 2 � 1 , 解得: � 香 2 且 � � 3 . 故选:C. 8.答案:A 解析:解:设每支百合花 x 元,每支玫瑰花 y 元, 根据题意得: 8� � 3� � �䁕� � 5�� � 8 , 整理得: 2� � 2� � 8 , � 2 支百合花比 2 支玫瑰花多 8 元. 故选:A. 设每支百合花 x 元,每支玫瑰花 y 元,根据总价 � 单价 � 购买数量结合小华一共花的钱比小红少 8 元, 即可得出关于 x、y 的二元一次方程,整理后即可得出结论. 本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键. 9.答案:C 解析: 本题主要考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质和三角形的外角性质是 解决问题的关键 . 由平行线的性质求出 ���� � 12䁥� ,再求出 ���� � 3䁥� ,然后根据三角形的外角性 质即可得出结论. 解: � ������ , �� � 䁕䁥� , � �� � ���� � 18䁥� , � ���� � 12䁥� , � ���� � 12䁥� � �䁥� � 3䁥� , � ��ᦙ� � �� � ���� � �5� � 3䁥� � 75� . 故选 C. 10.答案:B 解析:解: � 抛物线开口方向向上,则 � 香 䁥 , � � 2� 香 䁥 . 抛物线与 y 轴交于负半轴,则 � ܾ 䁥 , 所以 ��� ܾ 䁥 , 故 � 错误; � 如图所示,对称轴 � �� � 2� �� 1 ,则 � � 2� ,则 � � 2� � 䁥 ,故 � 正确; � 如图所示,抛物线与 x 轴有 2 个交点,则 � 2 � ��� 香 䁥 ,故 � 正确; � 对称轴 � �� 1 ,当 � �� � 与 � � 2 时的点是关于直线 � �� 1 的对应点, 所以 � �� � 与 � � 2 时的函数值相等,所以 �� � 2� � � 香 䁥 ,故 � 错误; 综上所述,正确的结论为 �� . 故选:B. � 根据抛物线的开口方向、抛物线对称轴位置、抛物线与 y 轴交点位置判定 a、b、c 的符号; � 根据对称轴的 � �� 1 来判断对错; � 由抛物线与 x 轴交点的个数判断对错; � 根据对称轴 � �� 1 来判断对错. 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求 2a 与 b 的关系,以及二次函数与 方程之间的转换,根的判别式的熟练运用. 11.答案: 3.7 � 1䁥 䁕 解析: 此题考查科学记数法的表示方法.科学记数法的表示形式为 � � 1䁥 � 的形式,其中 1 � ��� ܾ 1䁥 ,n 为整数,表示时关键要正确确定 a 的值以及 n 的值.科学记数法的表示形式为 � � 1䁥 � 的形式,其中 1 � ��� ܾ 1䁥 ,n 为整数.确定 n 的值时,要看把原数变成 a 时,小数点移动了多少位,n 的绝对值 与小数点移动的位数相同. 解:3700000 用科学记数法表示为: 3.7 � 1䁥 䁕 . 故答案为 3.7 � 1䁥 䁕 . 12.答案: � �� 2 解析: 本题考查的是函数自变量的取值范围有关知识,属于基础题. 根据题意可得 � � 2 � 䁥 即可解答. 解:由题意可得: � � 2 � 䁥 , 解得: � �� 2 . 故答案为 � �� 2 . 13.答案: �� � �� 或者 �� � �ᦙ 或者 �� � �� 解析: 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、 “AAS”、“HL” . 由 ���� � ���ᦙ 得到 ���� � �ᦙ�� ,加上 �� � �ᦙ ,所以当添加 �� � �� 时, 根据“AAS”可判断 � ���≌� �ᦙ� ;当添加 �� � �ᦙ 时,根据“ASA”可判断 � ���≌� �ᦙ� ;当添 加 �� � �� 时,根据“SAS”可判断 � ���≌� �ᦙ� . 解: � ���� � ���ᦙ , � ���� � ���� � ���ᦙ � ���� , � ���� � �ᦙ�� , 而 �� � �ᦙ , 当添加 �� � �� 时,根据“SAS”可判断 � ���≌� �ᦙ� ; 当添加 �� � �ᦙ 时,根据“ASA”可判断 � ���≌� �ᦙ� ; 当添加 �� � �� 时,根据“AAS”可判断 � ���≌� �ᦙ� ; 故答案为 �� � �� 或者 �� � �ᦙ 或者 �� � �� . 14.答案:圆锥 ��2� 解析: 本题考查了圆锥的计算,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了 数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.俯视图为圆的有圆锥, 圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,根据圆锥侧面积 � 底面周长 � 母 线长 � 2 ,可求得结果. 解:由三视图可知该几何体是圆锥. 由三视图可看出圆锥的底面直径为 2,母线长为 2, 故侧面积为 � � 1 � 2 � 2� . 15.答案:20 解析: 此题考查的是等腰三角形的性质和三角形周长的计算 . 注意分情况讨论:当三角形边长不明确指出是 腰长还是底边长时,要分情况讨论 . 当 8 为腰长时和当 8 为底边长是两种情况计算周长即可. 解:当等腰三角形腰长为 8 时,另两边分别为 8 和 4, � 8 � � 香 8 , � 能组成三角形, 此时三角形周长为: 8 � 8 � � � 2䁥 ; 当等腰三角形底边为 8 时,另两边分别为 4 和 4, � � � � � 8 , � 不能组成三角形, � 三角形周长为 20. 故答案为 20. 16.答案:2 解析: 本题考查了反比例函数图象上点的坐标特征,矩形的性质,根据矩形的对角线相等且互相平分求得 点 M 的坐标是解题的关键. 根据矩形的性质求得点 M 的坐标,将点 M 的坐标代入函数解析式求得 k 的值即可. 解: � 四边形 OABC 是矩形, � �� 与 AC 的交点 M 是 OB、AC 的中点. � � 点坐标是 ���2� , � 点 M 的坐标是 �2�1� . 将其代入 � � Ͳ � 得到: Ͳ � �� � 2 � 1 � 2 . 故答案是 2. 17.答案: 2 ��1 � 2 解析: 本题考查规律型:点的坐标、等腰直角三角形的性质等知识,解题的关键是从特殊到一般,探究规 律,利用规律解决问题,属于中考常考题型. 先求出 �1 、 �2 、 �3� 的坐标,探究规律后,即可根据规律解决问题. 解:由题意得 �� � ��1 � 2 , � ��1 � ��1 � 2 , �1�2 � �1�2 � � , �2�3 � �2�3 � 8 , � �1�2�䁥� , �2�䁕�䁥� , �3�1��䁥�� , 2 � 2 2 � 2 , 䁕 � 2 3 � 2 , 1� � 2 � � 2 , � � �� 的横坐标为 2 ��1 � 2 . 故答案为 2 ��1 � 2 . 18.答案:解:原式 � 1 � 2 � 1 � � � 1 2 � 1 � 2 � 1 � 2 � 䁥 . 解析:直接利用特殊角的三角函数值以及绝对值的性质、零指数幂的性质分别化简得出答案. 此题主要考查了实数运算,正确化简各数是解题关键. 19.答案:解: �� � 1��� � 5� � 䁥 , 则 � � 1 � 䁥 或 � � 5 � 䁥 , � � �� 1 或 � � 5 . 解析:因式分解法求解可得. 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、 因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键 20.答案:解: �1� 如图 � ,作直径 AD,连接 DC, � �� � �� ,且 �ൌ���� , � �� � ���� � �ൌ�� , � �� � �� , � �� � �ൌ�� , � �� 是直径, � �� � ���� � �䁥� , � �ൌ�� � ���� � �䁥� , � ���ൌ � �䁥� , 又 � 点 A 在 � � 上, � �ൌ 与 � � 相切; �2� 如图 � 作直径 AF, ᦙ� � �� ,连接 OB、OC, � �� � �� , �� � �� , � � 、A 在 BC 的垂直平分线上,即 AF 垂直平分 BC, � �� 平分 ���� , ᦙ� � �� , �� � �� , � ᦙ� � ᦙ� , �� � �� � 䁕 , 在 �� � ��� 中, � �� � 1䁥 , �� � 䁕 , � 由勾股定理得 �� � 8 , 设 � � 的半径为 x,在 �� � ��� 中 由勾股定理得: �8 � �� 2 � 䁕 2 � � 2 , � � � 25 � , 即 � � 的半径为 25 � , � �� � 1䁥 , �� � 䁕 , � �� � � , 由 � ��ᦙ∽� ��� 得: �� �� � �ᦙ �� , 代入解得: �ᦙ � 5 . 解析: �1� 如图 � ,作直径 AD,连接 DC,根据等腰三角形和平行线的性质得到 �� � ���� � �ൌ�� , 求得 �� � �ൌ�� ,根据圆周角定理得到 ���ൌ � �䁥� ,于是得到结论; �2� 如图 � 作直径 AF, ᦙ� � �� ,连接 OB、OC,根据线段垂直平分线的判定定理得到 O、A 在 BC 的垂直平分线上,即 AF 垂直平分 BC,根据角平分线的性质得到 ᦙ� � ᦙ� , �� � �� � 䁕 ,解直角 三角形即可得到结论. 本题考查了切线的判定和性质,圆周角定理,垂径定理,勾股定理,等腰三角形的性质,正确的作 出辅助线是解题的关键. 21.答案: �1�2䁥䁥 ,64 ; �2��3䁕 ; �3� 全校学生中家庭藏书 200 本以上的人数为: 2䁥䁥䁥 � 䁕䁕 2䁥䁥 � 䁕䁕䁥� 人 � , 答:全校学生中家庭藏书 200 本以上的人数为 660 人. 解析: 本题考查的是统计表和扇形统计图的综合运用.读懂统计图,从不同的统计表和统计图中得到必要 的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小. �1� 根据“C”的人数和在扇形图中所占的百分比,先求出样本容量,再根据“B”的百分比计算出 a 的值; �2� 利用圆心角计算公式,即可得到“A”对应的扇形的圆心角; �3� 依据家庭藏书 200 本以上的人数所占的比例,即可估计该校家庭藏书 200 本以上的人数. 解析: 解: �1� 因为“C”有 50 人,占样本的 25㌠ , 所以样本 � 5䁥 � 25㌠ � 2䁥䁥� 人 �因为“B”占样本的 32㌠ , 所以 � � 2䁥䁥 � 32㌠ � 䁕�� 人 �故答案为:200,64; �2� “A”对应的扇形的圆心角 � 2䁥 2䁥䁥 � 3䁕䁥� � 3䁕� , 故答案为:36; �3� 见答案. 22.答案:解: �1�� � 15䁥 3 � 5䁥 , � � 5.5 � 3䁥䁥�15䁥 2�5䁥 � � ; �2� 设乙车与 A 地的路程 s 与甲车离开 A 地的时间 t 之间的函数关系式为 � 乙 � Ͳ� � � , 将 �2�䁥� 、 �5�3䁥䁥� 代入 � � Ͳ� � � , 䁥 � 2Ͳ � � 3䁥䁥 � 5Ͳ � � ,解得: Ͳ � 1䁥䁥 � �� 2䁥䁥 , � � 乙 � 1䁥䁥� � 2䁥䁥�2 � � � 5� . 当 � 乙 � 1䁥䁥� � 2䁥䁥 � 15䁥 时, � � 3.5 . 答:两车在途中相遇时 t 的值为 3.5 ; �3� 䁕 5 或 1� 5 . 解析: 解: �1� 见答案; �2� 见答案; �3� 当 � � � 3 时, � 甲 � 5䁥� ; 当 3 � � � � 时, � 甲 � 15䁥 ; 当 � � � � 5.5 时, � 甲 � 15䁥 � 2 � 5䁥�� � �� � 1䁥䁥� � 25䁥 . � � 甲 � 5䁥��䁥 � � � 3� 15䁥�3 � � � �� 1䁥䁥� � 25䁥�� � � � 5.5� . 令 �� 甲 � � 乙 � � 䁕䁥 ,即 �5䁥� � 1䁥䁥� � 2䁥䁥� � 䁕䁥 , �15䁥 � 1䁥䁥� � 2䁥䁥� � 䁕䁥 或 �1䁥䁥� � 25䁥 � 1䁥䁥� � 2䁥䁥� � 䁕䁥 , 解得: �1 � 1� 5 , �2 � 2䁕 5 � 舍去 � , �3 � 2� 1䁥 � 舍去 � , �� � �1 1䁥 � 舍去 � ; 当 䁥 � � � 2 时,令 � 甲 � 5䁥� � 䁕䁥 ,解得: � � 䁕 5 . 综上所述:当两车相距 60 千米时, � � 䁕 5 或 1� 5 . 故答案为: 䁕 5 或 1� 5 . �1� 根据速度 � 路程 � 时间即可求出 a 值,再根据时间 � 路程 � 速度算出 b 到 5.5 之间的时间段,由此 即可求出 b 值; �2� 观察图形找出两点的坐标,利用待定系数法即可求出 � 乙关于 t 的函数关系式,令 � 乙 � 15䁥 即可 求出两车相遇的时间; �3� 分 䁥 � � � 3 、 3 � � � � 和 � � � � 5.5 三段求出 � 甲关于 t 的函数关系式,二者做差令其绝对值等 于 60 即可得出关于 t 的函数绝对值符号的一元一次方程,解之即可求出 t 值,再求出 䁥 � � � 2 时, � 甲 � 5䁥� � 䁕䁥 中 t 的值.综上即可得出结论. 本题考查了一次函数的应用、待定系数法求函数解析式以及解含绝对值符号的一元一次方程,解题 的关键是: �1� 根据数量关系列式计算; �2� 根据点的坐标利用待定系数法求出函数关系式; �3� 根据 数量关系求出 � 甲关于 t 的函数关系式. 23.答案: �1� 证明:由折叠的性质可知, ��� � �� � �� , ��� � �� � �䁥� , 在 � ��ᦙ 和 � ���ᦙ 中, �� � ��� ��ᦙ� � ��ᦙ�� �� � ��� � �� ��ᦙ≌� ���ᦙ ; �2� 解: �� ��ᦙ≌� ���ᦙ , � �ᦙ � ��ᦙ , 在 �� � �ᦙ�� 中, �ᦙ 2 � ��ᦙ 2 � ��� 2 ,即 �8 � �ᦙ� 2 � �ᦙ 2 � � 2 , 解得, �ᦙ � 3 ; �3�� 解析: 本题主要考查的是翻折的性质、勾股定理的应用,利用面积求得 戀� � 戀� 是解题的关键. �1� 根据折叠的性质得到 ��� � �� � �� , ��� � �� � �䁥� ,利用 AAS 定理证明; �2� 根据全等三角形的性质得到 �ᦙ � ��ᦙ ,根据勾股定理计算即可; �3� 连接 PE,根据三角形的面积公式计算. 解: �1� 见答案; �2� 见答案; �3� 解:连接 PE, �� ��ᦙ≌� ���ᦙ , � ᦙ� � ᦙ� , � ���ᦙ戀 � ��ᦙ�戀 � ��ᦙ�� , � 1 2 � �ᦙ � 戀� � 1 2 � ᦙ� � 戀� � 1 2 � ᦙ� � �� , � 戀� � 戀� � �� � � , 故答案为:4. 24.答案:解: �1� 将点 A、B 的坐标代入函数表达式得: �� � 2� � � � 䁥 1䁕� � �� � � � 䁥 , 解得: � �� 1 2 � � 1 , 故函数的表达式为: � �� 1 2 � 2 � � � � ; �2� 由 �1� 得:顶点 C 的坐标为 �1� � 2 � , � �� � � 轴, � ��1�䁥� , 则 �� � � � 1 � 3 , � � 是 BC 的中点,则点 �� 5 2 � � � � , 将 D、H 的坐标代入一次函数 � � Ͳ� � � 的表达式并解得: 直线 BH 的表达式为: � � 3 2 � � 3 2 , � 点 ᦙ�䁥� � 3 2 � ; �3� �� ��� 和 � ᦙ�� 有公共边 BC, � ����� ��ᦙ�� � �� ᦙ� , � �� ᦙ� � 3 2 , 设点 ����䁥� ,则点 ������ , � �� 1 2 � 2 � � � � , 则点 �� ��� 2 � 1 2 �� , 则直线 DH 的表达式为: � � � ��� � � 1 2 ��� � 2� �� �ᦙ , �� � � �� 1 2 �� � 2��� � �� , 由 �� ᦙ� � 3 2 , 解得: � � 8 5 , �� � 8 5 , �� � � � 8 5 � 12 5 , �� � 1䁥8 25 , 则 tan���� � �� �� � � 5 , 点 D 是 BC 的中点, � ���� � ���� , � 则 tan���� � � 5 . 解析: �1� 将点 A、B 的坐标代入函数表达式得: �� � 2� � � � 䁥 1䁕� � �� � � � 䁥 ,即可求解; �2� 由 �1� 得:顶点 C 的坐标为 �1� � 2 � , �� � � 轴,则 ��1�䁥� ,则 �� � � � 1 � 3 ,则点 �� 5 2 � � � � ,即 可求解; �3� � ��� 和 � ᦙ�� 由公共边 BC,则 ����� ��ᦙ�� � �� ᦙ� , ���� � ���� ,则 tan���� � � 5 ,即可求解. 本题考查的是二次函数综合运用,涉及到三角形面积的计算、一次函数等,其中 �3� ,利用 �� ᦙ� � 3 2 求 出点 H 的坐标,是本题解题的关键.查看更多