高中数学第一章算法初步1_3算法案例第1课时预习导航新人教A版必修3

高中数学第一章算法初步1_3算法案例第1课时预习导航新人教A版必修3

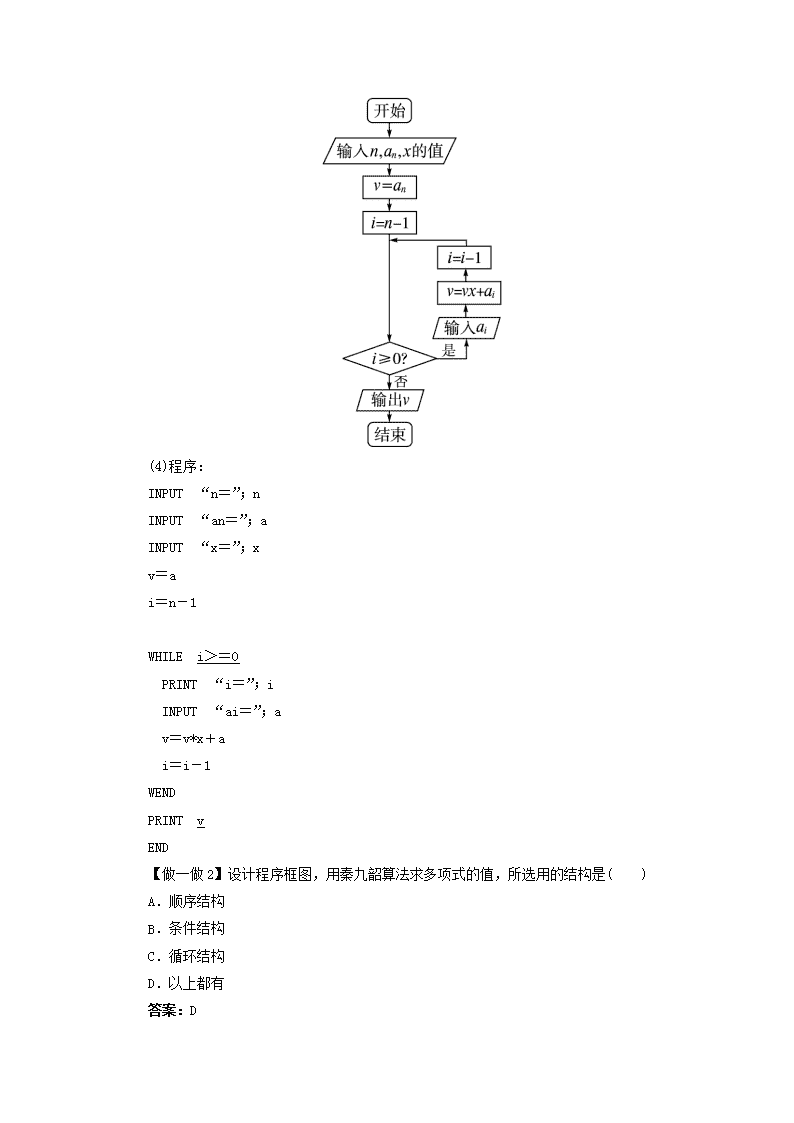
高中数学 第一章 算法初步 1.3 算法案例（第 1 课时）预习导航 新 人教 A 版必修 3 1．理解辗转相除法与更相减损术的步骤，了解其执行过程，并会求最大公约数． 2．掌握秦九韶算法，了解它提高计算效率的实质，并会求多项式的值． 3．进一步体会算法的基本思想． 1．辗转相除法与更相减损术 (1)辗转相除法． ①算法步骤： 第一步，给定两个正整数 m，n. 第二步，计算 m 除以 n 所得的余数 r. 第三步，m＝n，n＝r. 第四步，若 r＝0，则 m，n 的最大公约数等于 m；否则返回第二步． ②程序框图如图所示． ③程序： INPUT m，n DO r＝m MOD n m＝n n＝r LOOP UNTIL r＝0 PRINT m END (2)更相减损术． 算法分析： 第一步，任意给定两个正整数，判断它们是否都是偶数．若是，用 2 约简；若不是，执 行第二步． 第二步，以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小 数．继续这个操作，直到所得的差与减数相等为止，则这个数(等数)或这个数与约简的数的 乘积就是所求的最大公约数． 【做一做 1】用更相减损术求 294 和 84 的最大公约数时，第一步是__________． 解析：由于 294 和 84 都是偶数，先用 2 约简． 答案：用 2 约简 2．秦九韶算法 (1)概念：求多项式 f(x)＝anxn＋an－1xn－1＋…＋a1x＋a0 的值时，常用秦九韶算法，这种 算法的运算次数较少，是多项式求值比较先进的算法，其实质是转化为求 n 个一次多项式的 值，共进行 n 次乘法运算和 n 次加法运算．其过程是： 改写多项式为： f(x)＝anxn＋an－1xn－1＋…＋a1x＋a0 ＝(anxn－1＋an－1xn－2＋…＋a1)x＋a0 ＝((anxn－2＋an－1xn－3＋…＋a2)x＋a1)x＋a0＝… ＝(…((anx＋an－1)x＋an－2)x＋…＋a1)x＋a0. 设 v1＝anx＋an－1， v2＝v1x＋an－2， v3＝v2x＋an－3， …… vn＝vn－1x＋a0. (2)算法步骤： 第一步，输入多项式的次数 n、最高次项的系数 an 和 x 的值． 第二步，将 v 的值初始化为 an，将 i 的值初始化为 n－1. 第三步，输入 i 次项的系数 ai. 第四步，v＝vx＋ai，i＝i－1. 第五步，判断 i 是否大于或等于 0.若是，则返回第三步；否则，输出多项式的值 v. (3)程序框图如图所示． (4)程序： INPUT “n＝”；n INPUT “an＝”；a INPUT “x＝”；x v＝a i＝n－1 WHILE i＞＝0 PRINT “i＝”；i INPUT “ai＝”；a v＝v*x＋a i＝i－1 WEND PRINT v END 【做一做 2】设计程序框图，用秦九韶算法求多项式的值，所选用的结构是( ) A．顺序结构 B．条件结构 C．循环结构 D．以上都有 答案：D