八年级下数学课件八年级下册数学课件《三角形中的角平分线》 北师大版 (5)_北师大版

八年级下数学课件八年级下册数学课件《三角形中的角平分线》 北师大版 (5)_北师大版

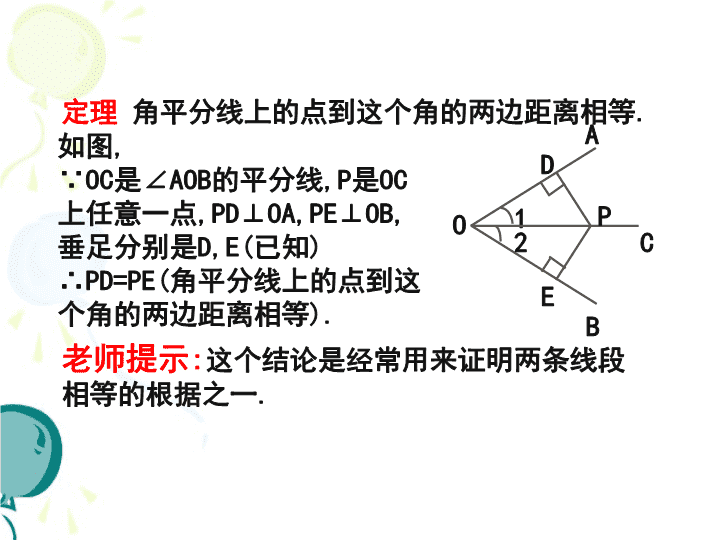
1.4 角平分线 (2) 一 回顾与思考 定理 角平分线上的点到这个角的两边距离相等. 老师提示:这个结论是经常用来证明两条线段 相等的根据之一. 如图, ∵OC是∠AOB的平分线,P是OC 上任意一点,PD⊥OA,PE⊥OB, 垂足分别是D,E(已知) ∴PD=PE(角平分线上的点到这 个角的两边距离相等). C B 1 A 2 P D E O 逆定理 在一个角的内部,且到角的两边距离 相等的点,在这个角的平分线上. 如图, ∵PD=PE, PD⊥OA,PE⊥OB,垂足分 别是D,E(已知), ∴点P在∠AOB的平分线上.(在一 个角的内部,且到角的两边距离相 等的点,在这个角的平分线上). 老师提示:这个结论又是经常用来证明点在直线 上(或直线经过某一点)的根据之一. C B 1 A 2 P D E O 二 探究新知 剪一个三角形纸片通过折叠 找出每个角的平分线. 结论:三角形三个角的平分线相交于一点. 你想证明这个命题吗? 观察这三条角平分线,你发 现了什么? 你能证明这个命题吗? 利用尺规作出三角形三个 角的角平分线. 结论:三角形三个角的角平分线相交于一点. 老师期望:你能写出规范的证明过程. 你想证明这个命题吗?你能证明这个命题吗? 再观察这三条角平分线,你 又发现了什么?与同伴交流. 思 考 分 析 命题:三角形三个角的平分线相交于一点. 基本思路:我们知道,两条直线相交只有一个 交点.要想证明三条直线相交于一点,只要能证明 两条直线的交点在第三条直线上即可.这时可以考 虑前面刚刚学到的逆定理. 如何证三条直线交于一点？ A B C P MND E F 如图,设△ABC的角平分线BM,CN相交于点P, 过点P分别作BC,AC,AB的垂线,垂足分别E,F,D. ∵BM是△ABC的角平分线,点P在BM上 ∴PD=PE(角平分线上的点到这个 角的两边距离相等). 同理,PE=PF∴PD=PF. . ∴点P在∠BAC的平分线上(在一个角的内部,且 到角两边距离相等的点,在这个角的平分线上). ∴△ABC的三条角平分线相交于一点P. 定理:三角形的三条角平分线相交于一点,并且 这一点到三边的距离相等. 如图,在△ABC中, ∵BM,CN,AH分别是△ABC的三条 角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点 的根据之一这个交点叫做三角形的内心. A B C P MND E F ∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的 三条角平分线相交于一点,并且这一点到三边的 距离相等). H [例3]如图，在△ABC中．AC=BC，∠C=90°，AD是 △ABC的角平分线，DE⊥AB，垂足为E． (1)已知CD=4 cm，求AC的长； (2)求证：AB=AC+CD． 练一练 D A B E C (1)解：∵AD是△ABC的角平分线，∠C=90°，DE⊥AB ∴DE=CD=4cm ∵AC=BC ∴∠B=∠BAC(等边对等角) ∵∠C=90°，∴∠B= ×90°=45°． ∴∠BDE=90°-45°=45°． ∴BE=DE(等角对等边)． 在等腰直角三角形BDE中 (勾股定理)， ∴AC=BC=CD+BD=(4+ )cm． 1 2  2BD 2DE 4 2cm 4 2 [例3]如图，在△ABC中．AC=BC，∠C=90°，AD是 △ABC的角平分线，DE⊥AB，垂足为E． (1)已知CD=4 cm，求AC的长； (2)求证：AB=AC+CD． 练一练 D A B E C (2)证明：由(1)的求解过程可知， Rt△ACD≌Rt△AED(HL) ∴AC=AE（全等三角形的对应边相等） ∵BE=DE=CD， ∴AB=AE+BE=AC+CD． 三 挑战自我 1.已知:如图,∠C=900, ∠B=300, AD是Rt△ABC 的角平分线. 求证:BD=2CD. 老师期望:你能写出规范的证明过程. A B CD 证明 ∵ ∠C=90°∴ ∠B= 30° ∴Rt△ABC中，AB=2BC, ∠BAC= 60° ∵ AD是△ABC的角平分线 ∴ ∠BAD= ∠DAC= 30°,AD=BD ∴ Rt△ACD中，AD=2CD ∴ BD=2CD 2.已知:如图,△ABC的外角∠CBD和∠BCE的角 平分线相交于点F. 求证:点F在∠DAE的平分线上. A B C FD E 证明： ∵ BF是∠CBD的角平分线 ∴ F到BC,AD的距离相等 ∵ BF是∠CBD的角平分线 ∴ F到BC,AE的距离相等 ∴ F到AD,AE的距离相等 从而点F在∠DAE的平分线上. 3.已知:如图,P是∠AOB 平分线上的一个点，并且 PC⊥OA,PD⊥OB,垂足分别是 C,D. 求证: (1)OC=OD; (2)OP是CD的垂直平分线. B A P D C O 证明(1) ∵P为P是∠AOB平分线上的一个点 PC⊥OA,PD⊥OB ∴PC=PD Rt△POC和 Rt△POD ∵ OP=OP Rt△POC ≌ Rt△POD ∴OC=OD (2) 由PC=PD得P在CD的垂直平分线上 由OC=OD得O在CD的垂直平分线上 ∴OP是CD的垂直平分线. 拓展探索：如图,已知△ABC,作△ABC一个内 角和与它不相邻的两个外角的平分线,看它们是否 交于一点?这样的点有几个?如果以这个点为圆心, 这一点到三角形一边的距离为半径作圆,你能作出 这个图形吗? A B C 四 回顾与小结 定理:三角形的三条角平分线相交于 一点,并且这一点到三边的距离相等(这 个交点叫做三角形的内心). 如图,在△ABC中, ∵BM,CN,AH分别是△ABC的三条 角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点 的根据之一这个交点叫做三角形的内心. A B C P MND E F ∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的 三条角平分线相交于一点,并且这一点到三边的 距离相等). H 独立 作业 复习题 4,6,7题. 祝你成功！ 结束寄语 严格性之于数学家,犹如道德之于人. 证明的规范性在于：条理清晰，因果相 应,言必有据.这是初学证明者谨记和遵 循的原则.