北师大版数学八年级上册第一章勾股定理单元测试题

北师大版数学八年级上册第一章勾股定理单元测试题

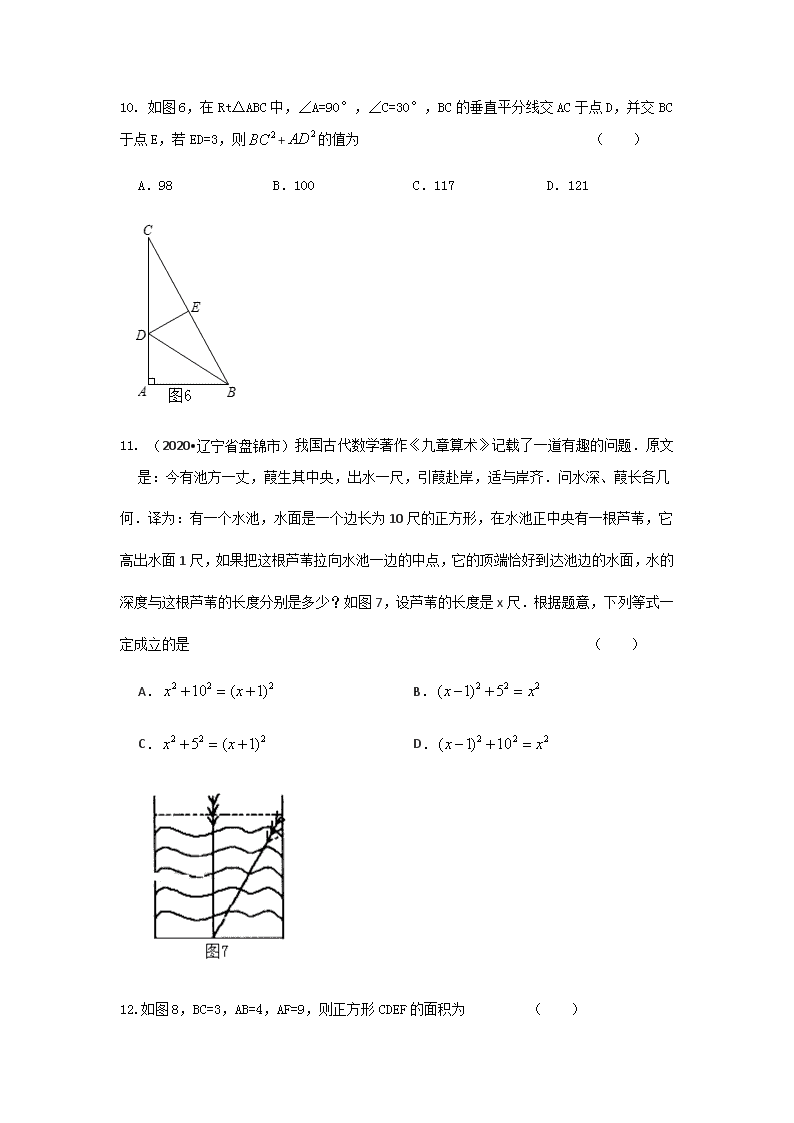
北师版数学八年级上册第一章勾股定理单元测试题 一、选择题（每题 3 分，共 12 题，满分 36 分） 1. 下列四组线段中，可以构成直角三角形的是 （ ） A．2，3，4 B．4，5，6 C．1.5，2.5，3 D．5,12,13 2. 如图，在直角三角形 ABC 中，∠B=90°，以下式子成立的是（ ） A. 2 2 2a b c  B. 2 2 2a c b  C． 2 2 2b c a  D． 2 2a c b  3. 直角三角形两直角边的平方和等于斜边的平方，在中国我们常称之为勾股定理，在国外 称之为 （ ） A．毕达哥拉斯定理 B．托勒密定理 C．蝴蝶定理 D．陈氏定理 4. 如图 2，点 E 在正方形 ABCD 内一点，满足∠AEB=90°．AE=6，BE=8，则阴影部分的面积 是 ( ) A． 48 B．60 C．76 D． 80 5. 如图 3，有一张直角三角形纸片，两直角边 AC=6，BC=8，将△ABC 折叠，使点 B 与点 A 重合，折痕为 DE，则 CD 等于 （ ） A. 4 25 B. 3 22 C. 4 7 D. 3 6. 设三角形 ABC 的三边长分别为 a,b,c，则一定能判定三角形是直角三角形的是 （ ） A．a=b=c B．a+b=c C． 2 2b a c  D． 2 2 2b a c  7.点 A 在数轴上表示的数是-2，点 B 表示的数是 1，点 C 是数轴外一点，且点 C 到数轴的距 离 C 为 4，则点 B 与点 C 的距离是 （ ） A．4 B．5 C．6 D．7 8. 我国古代数学家赵爽的"勾股方圆图"是由四个全等的直角三角形与中间的一个小正方形 拼成的一个大正方形(如图 4 所示).如果大正方形的面积是 13,小正方形的面积是 1,直角三 角形的两直角边长分别为 a,b,则下列结论错误的是 （ ） A. 2 2 13a b  B. 2( ) 1a b  C. ab=6 D. a+b=8 9. 如图 5，花园住宅小区有一块长方形绿化带，有极少数人为了避开拐角走“捷径”，在 草坪内走出了一条“路”．他们仅仅少走了（ ）步路，却踩伤了花草（假设 2 步为 1 米）． A．6 步 B．5 步 C．4 步 D．2 步 10. 如图 6，在 Rt△ABC 中，∠A=90°，∠C=30°，BC 的垂直平分线交 AC 于点 D，并交 BC 于点 E，若 ED=3，则 2BC + 2AD 的值为 （ ） A．98 B．100 C．117 D．121 11. （2020•辽宁省盘锦市）我国古代数学著作《九章算术》记载了一道有趣的问题．原文 是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几 何．译为：有一个水池，水面是一个边长为 10 尺的正方形，在水池正中央有一根芦苇，它 高出水面 1 尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的 深度与这根芦苇的长度分别是多少？如图 7，设芦苇的长度是 x 尺．根据题意，下列等式一 定成立的是 （ ） A． 2 2 210 ( 1)x x   B． 2 2 2( 1) 5x x   C． 2 2 25 ( 1)x x   D． 2 2 2( 1) 10x x   12.如图 8，BC=3，AB=4，AF=9，则正方形 CDEF 的面积为 （ ） A．13 B．15 C．106 D．122 二、填空题（每题 3 分，共 7 题，满分 21 分） 13. .(2020 年四川省雅安市)对角线互相垂直的四边形叫做“垂美”四边形，现有如图 9 所示的“垂美”四边形 ABCD，对角线 AC.BD 交于点 O．若 AD=2，BC=4，则 AB 2 + CD 2 = ． 14. （2020•湖北省黄冈市）我国古代数学著作《九章算术》中有这样一个问题：”今有池 方一丈，葭（jiā）生其中央，出水一尺．引葭赴岸，适与岸齐．问水深几何？”（注：丈， 尺是长度单位，1 丈＝10 尺）这段话翻译成现代汉语，即为：如图 10，有一个水池，水面 是一个边长为 1 丈的正方形，在水池正中央有一根芦苇，它高出水面 1 尺．如果把这根芦苇 拉向水池一边的中点，它的顶端恰好到达池边的水面，则水池里水的深度是 尺． 15. (2020•江苏省扬州市)《九章算术》是中国传统数学的重要著作之一，奠定了中国传统 数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地， 去根三尺，问折者高几何？”题意是：一根竹子原高 1 丈(1 丈＝10 尺)，中部有一处折断， 竹梢触地面处离竹根 3 尺，试问折断处离地面多高？答：折断处离地面 尺高． 16. （2020·威海）如图 11，四边形 ABCD 是一张正方形纸片，其面积为 25 2cm ．分别在 边 AB，BC，CD，DA 上顺次截取 AE=BF=CG=DH=acm，（AE＞BE），连接 EF，FG，GH，HE．分别 以 EF，FG，GH，HE 为轴将纸片向内翻折，得到四边形 1A 1B 1C 1D ，如图 12 所示，若四边 形 1A 1B 1C 1D 的面积为 9 2cm ，则 a=________． 17. （2020·湖南娄底）由 4 个直角边长分别为 a，b 的直角三角形围成 的“赵爽弦图”如 图 13 所示，根据大正方形的面积 2c 等于小正方形的面积 2( )a b 与 4 个直角三角形的面积 2ab 的和证明了勾股定理 2 2 2c a b  ，还可以用来证明结论：若 a＞0、b＞0 且 2 2a b 为 定值，则当 a b 时，ab 取得最大值． 18. （2020.台州）用四块大正方形地砖和一块小正方形地砖拼成如图 14 所示的实线图案， 每块大正方形地砖面积为 a，小正方形地砖面积为 b，依次连接四块大正方形地砖的中心得 到正方形 ABCD．则正方形 ABCD 的面积为 ．（用含 a，b 的代数式表示） 19. （2020·宁夏）2002 年 8 月，在北京召开的国际数学家大会会标取材于我国古代数学 家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正 方形（如图 15），且大正方形的面积是 15，小正方形的面积是 3，直角三角形的较短直角边 为 a，较长直角边为 b．如果将四个全等的直角三角形按如图 16 的形式摆放，那么图 5 中最 大的正方形的面积为 ． 三、解答题（满分 43 分） 20.（满分 6 分）判断下列三角形的形状 判断由线段 a. b. c 组成的三角形是不是直角三角形 （1）a=15，b=8，c=17；（2）a=13，b=14，c=15 21. （满分 5 分）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法” 给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图 17 或图 18 摆放时，都可以 用“面积法”来证明，下面是小聪利用图 17 证明勾股定理的过程： 将两个全等的直角三角形按图 17 所示摆放，其中∠DAB=90°，求证：a2+b2=c2 证明：连结 DB，过点 D 作 BC 边上的高 DF，则 DF=EC=b﹣A． ∵S 四边形 ADCB=S△ACD+S△ABC=b2+ab．又∵S 四边形 ADCB=S△ADB+S△DCB=c2+a（b﹣a） ∴b2+ab=c2+a（b﹣a）,∴a2+b2=c2 请参照上述证法，利用图 18 完成下面的证明．将两个全等的直角三角形按图 18 所示摆放， 其中∠DAB=90°．求证：a2+b2=c2 22. （满分 6 分）（2020 年山西省）阅读与思考 如图是小宇同学的数学日记，请仔细阅读，并完成相应的任务． ×年×月×日星期日 没有直角尺也能作出直角 今天，我在书店一本书上看到下面材料：木工师傅有一块如图 19 所示的四边形木板，他 已经在木板上画出一条裁割线 AB，现根据木板的情况，要过 AB 上的一点 C，作出 AB 的 垂线，用锯子进行裁割，然而手头没有直角尺，怎么办呢？ 办法一：如图 19，可利用一把有刻度的直尺在 AB 上量出 CD＝30cm，然后分别以 D，C 为圆心，以 50cm 与 40cm 为半径画圆弧，两弧相交于点 E，作直线 CE，则∠DCE 必为 90°． 办法二：如图 20，可以取一根笔直的木棒，用铅笔在木棒上点出 M，N 两点，然后把木 棒斜放在木板上，使点 M 与点 C 重合，用铅笔在木板上将点 N 对应的位置标记为点 Q， 保持点 N 不动，将木棒绕点 N 旋转，使点 M 落在 AB 上，在木板上将点 M 对应的位置标 记为点 R．然后将 RQ 延长，在延长线上截取线段 QS＝MN，得到点 S，作直线 SC，则∠ RCS＝90°． 我有如下思考：以上两种办法依据的是什么数学原理呢？我还有什么办法不用直角尺也 能作出垂线呢？…… 任务： （1）填空：“办法一”依据的一个数学定理是 勾股定理的逆定理 ； （2）根据“办法二”的操作过程，证明∠RCS＝90°； （3）①尺规作图：请在图 21 的木板上，过点 C 作出 AB 的垂线（在木板上保留作图痕 迹，不写作法）；②说明你的作法所依据的数学定理或基本事实（写出一个即可）． 23. （满分 5 分）已知：如图 22，以 Rt△ABC 的三边为斜边分别向外作等腰直角三角形．若 斜边 AB=3.求图中阴影部分的面积． 24. （满分 6 分）（2020.长春市）图 23、图 24、图 25 均是 3×3 的正方形网格，每个小正 方形的边长为 1，每个小正方形的顶点称为格点，线段 AB 的端点均在格点上，只用无刻度 的直尺，在给定的网格中，按下列要求以 AB 为边画△ABC． 要求：（1）在图 3 中画一个钝角三角形，在图 4 中画一个直角三角形，在图 5 中画一个锐角 三角形；（2）三个图中所画的三角形的面积均不相等；（3）点 C 在格点上． 25. （满分 8 分）（2020.温州）如图 26，在 △ ABC 和 △ DCE 中，AC＝DE，∠B＝∠DCE＝ 90°，点 A，C，D 依次在同一直线上，且 AB∥DE． （1）求证： △ ABC≌△DCE． （2）连结 AE，当 BC＝5，AC＝12 时，求 AE 的长． 26. （满分 8 分） （2020 年湖北省随州市）勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕 达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国 汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图 27），后人称之为“赵爽弦 图”，流传至今． （1）①请叙述勾股定理； ②勾股定理的证明，人们已经找到了 400 多种方法，请从下 列几种常见的证明方法中任选一种来证明该定理；（以下图形均满足证明勾股定理所需的 条件，图 28 ，图 29） （2）①如图 30，图 31, 图 32 以直角三角形的三边为边或直径，分别向外部作正方形、 半圆、等边三角形，这三个图形中面积关系满足 1S + 2S = 3S 的有 个； ②如图 33 所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案（图中阴 影部分）的面积分别为 1S ， 2S ，直角三角形面积为 3S ，请判断 1S ， 2S ， 3S 的关系并 证明； （3）如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向 外作正方形，重复这一过程就可以得到如图 34 所示的“勾股树”．在如图 35 所示的“勾股 树”的某部分图形中，设大正方形 M 的边长为定值 m，四个小正方形 A，B，C，D 的边长 分别为 a，b，c，d，已知∠1＝∠2＝∠3＝∠α，则当∠α变化时，回答下列问题：（结果 可用含 m 的式子表示） ① 2 2 2 2a b c d   = ； ②b 与 c 的关系为 ，a 与 d 的关系为 ． 参考答案： 北师版数学八年级上册第一章勾股定理单元测试题 选择题 1. D 2. B 3.A 4. C 5. C 6. D 7.B 8. D 9. C 10. C 11. B 12 C 二、填空题 13. 20 14. 12 15.4.55 16. 4 解析：设 BE=b，根据赵爽弦图的几何意义，得 a+b=5，a-b=3,解方程组，得 a=4. 17. = 解析：如图，作斜边 c 上高 h，∵ 2( )a b ≥0，∴ 2 2a b ﹣2ab≥0，又∵ 2 2 2a b c  ， 2 2a b 为定值，∴ab≤ 2 2 c ,∴ab 最大值为 2 2 c ,∵a，b 为直角边的直角三角形面积为： 1 1 2 2ab ch ，∴ 2 2 c =ch，∴h= 2 c ,根据直角三角形斜边上的中线等于斜边的一半，得 h 是 直角三角形斜边上的中线，∵h 是斜边上的高线，∴△ABC 是等腰直角三角形，∴a=b， ∴当 a=b 时，ab 的值最大.故应该填“=”． 18. 解：a+b 19. 27 解析：根据赵爽弦图的几何意义，得 2 2a b =15， 2-a)b（ =3，大正方形的面积为： 2a+b)（ ， ∵ 2-a)b（ =3，∴ 2 22a ab b  =3，∴15﹣2ab=3，∴2ab=12， ∴ 2a+b)（ = 2-a)b（ +4ab=3+2×12=27，或 2a+b)（ = 2 2a b +2ab=15+12=27. 三、解答题 20.解：（1）因为 28964225815 22  ， 28917 2  所以 222 17815  ，这个三角形是直角三角形 （2）因为 22515,3651961691413 222  所以 222 151413  ，这个三角形不是直角三角形 21.证明：连结 过点 B 作 DE 边上的高 BF，则 BF=b﹣a， ∵S 五边形 ACBED= S△ACB+S△ABE+S△ADE=ab+b2+ab， 又∵S 五边形 ACBED= S△ACB+S△ABD+S△BDE=ab+c2+a（b﹣a）， ∴ ab+b2+ab=ab+c2+a（b﹣a）， ∴a2+b2=c2． 22.解：（1）∵CD＝30，DE＝50，CE＝40，∴CD2+CE2＝302+402＝502＝DE2， ∴∠DCE＝90°， 故“办法一”依据的一个数学定理是勾股定理的逆定理； 故答案为：勾股定理的逆定理； （2）由作图方法可知，QP＝QC，QS＝QC， ∴∠QCR＝∠QRC，∠QCS＝∠QSC， ∵∠SRC+∠RCS+∠QRC+∠QSC＝180°， ∴2（∠QCR+∠QCS）＝180°， ∴∠QCR+∠QCS＝90°， 即∠RCS＝90°； （3）①如图③所示，直线 PC 即为所求； ②答案不唯一，到一条线段两个端点距离相等的点，在这条线段的垂直平分线上． 23. 解：根据勾股定理，得 2 2 2 22AC AD DC AD   ， 2 2 2 22BC CE BE CE   , 2 2 2 22AB AF BF AF   ， ADCS = 21 1 2 2AD DC AD  , BCES = 21 1 2 2CE BE CE  , ABFS = 21 1 2 2AF BF AF  ,∴ ADCS + BCES + ABFS = 21 2 AD + 21 2 CE + 21 2 AF = 21 4 AC + 21 4 CB + 21 4 AB = 2 21 ( )4 AC CB + 21 4 AB ,∵ 2 2 2AC CB AB  , ∴阴影面积为： 21 4 AB + 21 4 AB = 21 2 AB = 9 2 . 24. 解析：如图所示：即为符合条件的三角形． 25. 证明：（1）∵AB∥DE，∴∠BAC＝∠D，又∵∠B＝∠DCE＝90°，AC＝DE， ∴△ABC≌△DCE（AAS）； （2）∵△ABC≌△DCE，∴CE＝BC＝5，∵∠ACE＝90°， ∴AE＝ ＝ ＝13． 26. 解析：（1）①如果直角三角形的两条直角边分别为 a，b，斜边为 c，那么 2 2 2a b c  ． （或者：在直角三角形中，两条直角边的平方和等于斜边的平方．） （2）证明：在图 11 中，大正方形的面积等于四个全等的直角三角形的面积与中间小正 方形面积的和．即 2 21 ab 4 ( )2c b a    ，化简得： 2 2 2a b c  ． 在图 12 中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和． 即 2 21 ab 4 ( )2c b a    ，化简得： 2 2 2a b c  ． 在 图 13 中 ， 梯 形 的 面 积 等 于 三 个 直 角 三 角 形 的 面 积 的 和． 21 1 1ab 2 ( )( )2 2 2c a b a b     ，化简得： 2 2 2a b c  ． （2）①三个图形中面积关系满足 1S + 2S = 3S 的有 3 个；②结论： 1S + 2S = 3S ．理由如 下： ∵ 1S + 2S = 2 2 2 3 1 1 1( ) ( ) ( )2 2 2 2 2 2 a b cS     ，∴ 1S + 2S = 2 2 2 3 1 ( )8 a b c S    ， ∵ 2 2 2a b c  ，∴ 1S + 2S = 3S ． （3）① 2 2 2 2 2a b c d m    ；②b 与 c 的关系为 b=c，a 与 d 的关系为 a+d=m．