- 2021-05-27 发布 |
- 37.5 KB |
- 67页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
部编版数学下册四年级单元期中期末试卷
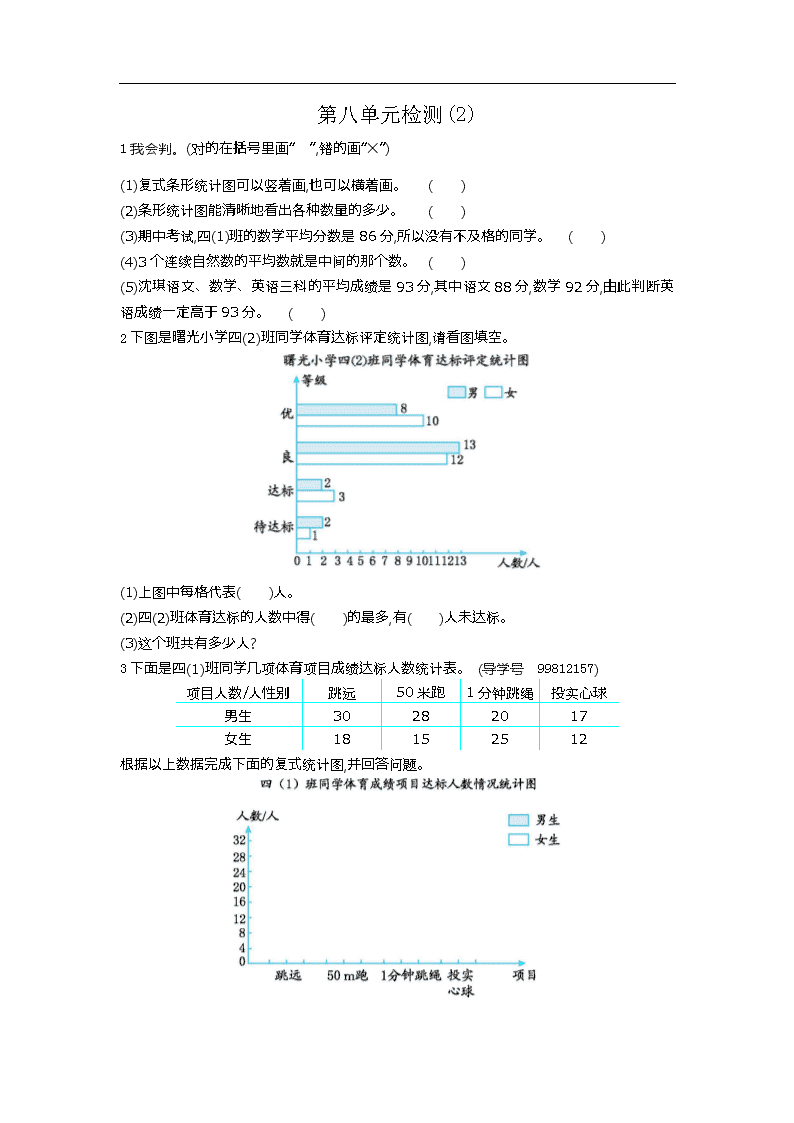
第八单元检测(2) 1 我会判。(对的在括号里画“ ”,错的画“✕”) (1)复式条形统计图可以竖着画,也可以横着画。 ( ) (2)条形统计图能清晰地看出各种数量的多少。 ( ) (3)期中考试,四(1)班的数学平均分数是 86 分,所以没有不及格的同学。 ( ) (4)3 个连续自然数的平均数就是中间的那个数。 ( ) (5)沈琪语文、数学、英语三科的平均成绩是 93 分,其中语文 88 分,数学 92 分,由此判断英语 成绩一定高于 93 分。 ( ) 2 下图是曙光小学四(2)班同学体育达标评定统计图,请看图填空。 (1)上图中每格代表( )人。 (2)四(2)班体育达标的人数中得( )的最多,有( )人未达标。 (3)这个班共有多少人? 3 下面是四(1)班同学几项体育项目成绩达标人数统计表。 (导学号 99812157) 项目人数/人性别 跳远 50 米跑 1 分钟跳绳 投实心球 男生 30 28 20 17 女生 18 15 25 12 根据以上数据完成下面的复式统计图,并回答问题。 (1)( )项目男生达标人数最多,( )项目女生达标的人数最多。 (2)全班达标人数最少的项目是( )。 (3)这个班至少有( )人。 4 李芳参加歌咏比赛,七位评委的打分分别是 89 分、91 分、61 分、91 分、92 分、92 分、 93 分。 (导学号 99812158) (1)这七位评委打分的平均分是多少? (2)如果去掉一个最高分和一个最低分后的平均分是多少? 5 下面是琳琳星期一到星期五完成家庭作业所用时间的记录表。 星期 一 二 三 四 五 时间/分 30 35 25 30 40 (导学号 99812159) (1)她平均每天完成作业要用多长时间? (2)她每天晚上写完作业后还要在 19:30 练习毛笔字,最晚要在什么时间开始做作业? 6 爸爸去爬山,上山时的速度是 5 千米/时,3 小时到达山顶,下山时沿原路返回,只用 2 小时到山 脚下。爸爸上、下山的平均速度是多少? (导学号 99812160) 第八单元检测 1.(1) (2) 解析:这两道题考查的是复式条形统计图的特点和画法。复式条形统计图有横向复式条形统 计图,也有纵向复式条形统计图。条形统计图的特点就是用直条的长短来表示数量的多少,可 以直观地反映出数量的多少。 (3)✕ (4) (5) 解析:这些题考查的是平均数的意义和特点。平均数是借助平均分的意义通过计算得到的,它 可以反映一组数据的一般情况,但它并不是每个数的个体情况。(3)题平均分是 86 分,并不是 每个同学都得了 86 分,应该有高于 86 分的,也有低于 86 分的,也可能会有不及格的同学。(4) 题可以举例来判断,假设这 3 个连续自然数是 4、5、6,采用“移多补少”的方法,则这三个数 的平均数正好是 5,是中间的那个数。(5)题已知语文、数学、英语三科的平均分是 93 分,又知 语文和数学都低于 93 分,根据平均数的特点来思考,要使平均分达到 93 分,英语分必须高于平 均 分 才 能 补 给 语 文 和 数 学 。 也 可 以 通 过 计 算 得 出 英 语 的 实 际 分 数 , 列 式 为 93×3-88-92=99(分)。 2.(1)1 (2)良 3 (3)8+10+13+12+2+3+2+1=51(人) 答:这个班共有 51 人。 解析:此题考查的是对复式条形统计图的分析情况。(1)题可以直接从统计图中看出,每格代表 1 人。(2)题通过观察直条的长度就可以直接得出“良”等级的人数最多;未达标的人数通过 计算得出,2+1=3(人)。(3)题把所以人数相加即可得到。 3. (1)跳远 1 分钟跳绳 (2)投实心球 (3)55 解析:此题考查的是制作并分析复式条形统计图的能力。画条形统计图的每一个直条时,一定 要看清数据和图例,准确画图。(1)(2)题通过比较直条的长度便知。(3)题易错,要求这个班至 少有多少人,看统计图可知,男生至少有 30 人,女生至少有 25 人,所以这个班至少有 30+25=55(人)。 4.(1)(89+91+61+91+92+92+93)÷7=87(分) 答:这七位评委打分的平均分是 87 分。 (2)(89+91+91+92+92)÷5=91(分) 答:如果去掉一个最高分和一个最低分后的平均分是 91 分。 解析:此题考查的是平均数的求法。本题用“总分÷人数”即可。计算后发现,平均数会受到 偏大数和偏小数的影响。 5.(1)(30+35+25+30+40)÷5=32(分) 答:她平均每天完成作业要用 32 分钟。 (2)她每天晚上写完作业后还要在 19:30 练习毛笔字,最晚要在 18:50 开始做作业。 解析:此题考查的是求平均数,以及利用平均数来解决问题。(1)题求平均每天完成作业所用时 间,就用这五天的作业总用时除以 5 即可。(2)题求最晚要在什么时间开始做作业,这个不能用 平均用时做标准,因为星期二和星期五的作业用时比平均用时长,如果在 18:58 开始做作业的 话,到 19:30 完不成作业。所以要以最长的做作业用时为标准,即按 40 分钟的做作业用时来计 算,应在 18:50 开始写作业。 6.5×3×2÷(3+2)=6(千米/时) 答:爷爷上、下山的平均速度是 6 千米/时。 解析:此题考查的是平均数的求法。本题是求平均速度,关系式是平均速度=总路程÷总时间, 根据此关系式先求出总路程。从上山的速度和时间可以求出上山的路程为 5×3=15(千米),下 山时沿原路返回,说明下山的路程也是 15 千米,则总路程是 15×2=30(千米)。上、下山的总时 间是 3+2=5(小时)。得出上、下山的平均速度是 30÷5=6(千米/时)。 第二单元检测(2) 1 下面的图形分别是从什么位置看到的?连一连。 (1) (2) 2 分别画出从前面、上面和左面看到的图形。 (1) (2) 3 我会选。(将正确答案的序号填在括号里) (1)从前面观察左图,所看到的图形是( )。 (2)从左面分别观察下面的物体,( )看到的是 。 (3)从左面观察下面的物体,看到的图形相同的一组是( )。 (4)观察左边物体,从前面看是( ),从上面看是( ),从左面看是( )。 4 我会填。 (1)从前面看到 的是( ),看到 的是( )。 (2)从左面看到 的是( ),看到 的是( )。 (3)从上面看到 的是( ),看到 的是( )。 5 按要求填空。(导学号 99812025) (1)上面 3 个物体,从什么位置看到的形状相同? (2)从哪面看到的形状不同? 6 想一想,画一画。(导学号 99812026) (1)在上图中再放一个 ,使得从上面看到的形状不变,有几种放法? (2)在图中再放一个 ,使得从左面和前面看到的形状都不变,有几种放法? 答案 1.(1) (2) 解析:此题考查的是从不同位置观察物体。连线前先认真观察,再确定位置,最后连图形。 2.(1) (2) 解析:此题考查的是画出从不同位置观察到的图形的知识。在方格纸上画之前,一定要认真观 察,先仔细数一数从不同位置观察时能看到几个小正方形,再观察这些小正方形的排列方式, 最后画下来。 3.(1)B (2)C 解析:(1)、(2)题考查的是从特定位置观察物体所看到的形状。第(1)题,从前面可以看到 3 个 小正方形,分两层,上层 1 个,下层 2 个,所以选 B。第(2)题,从左面看到是 ,说明这个物体有两 层,而且在一列上,所以选 C。 (3)A 解析:此题考查的是观察物体的知识。从同一位置观察不同物体,看到的形状可能是相同的。 从左面观察,A 组分别是 和 ;B 组分别是 和 ;C 组分别是 和 。 (4)A C B 解析:此题考查的是从不同位置观察同一物体所看到的形状。从前面看,是 2 层 3 列,所以选 A; 从左面看,是 4 列 2 层,所以选 B;从上面看,是 4 行 3 列,所以选 C。 4.(1)C A、E (2)C、D A、E (3)B C、D 解析:此题考查的是观察物体的知识。在同一位置观察不同物体,看到的形状可能相同,也可能 不同。解答此题时,选定位置一一认真观察,便可找到所看到的形状。 5.(1)从前面、左面(右面)看到的形状相同。 (2)从上面看到的形状不同。 解析:此题考查的是观察物体的知识。从不同位置观察不同的物体,看到的形状可能相同,也可 能不同。如从前面观察,看到的都是 。同理,分别找出看到相同形状和不同形状的位置。 6.(1)有 3 种放法。 解析:此题考查的知识点是从观察到的形状动手摆物体。此题要求多放一个 ,但从上面看到 的形状不变有几种放法。我们知道,从上面观察,看到的是物体的上面,所以,放在原来的任何一 列的上面都不会改变形状。如下图所示。 (2)应该放在第一列的后面或第三列的前面。 解析:此题考查的是从观察到的形状动手摆物体。此题要求多放 1 个 ,但从左面和前面看到 的形状不变有几种放法。先考虑从前面看到的不变,只能放在原图的第三列的前面或第一列 的后面,还不能多出一排,否则就会使在左面看到的形状改变。所以只能放在第三列的前面(竖 放)或第一列的后面。如下图所示。 第九单元检测(2) 1 我会填。 (1)3 只鸡和 6 只兔共( )条腿,6 只兔比 6 只鸡多( )条腿。 (2)鸡和兔共有 7 只,共有 24 条腿。鸡和兔各有多少只? ①假设 7 只全是鸡,那么一共有( )条腿,这样就比 24 条腿少了( )条;要使腿正好是 24 条,就要在其中( )只上各添 2 条腿。这说明兔有( )只,鸡有( )只。 ②假设 7 只全是兔,那么一共有( )条腿,就比 24 条腿多了( )条;要使腿正好是 24 条,就 要在其中( )只上各减少 2 条腿。这说明鸡有( )只,兔有( )只。 (3)琳琳去买铅笔,她用10元钱买了价钱为5角和1元的两种铅笔共13 支。5角的铅笔有( ) 只,1 元的铅笔有( )支。 (4)科学知识抢答赛,答对一题加 10 分,答错一题扣 6 分。 2 我会选。(将正确答案的序号填在括号里) (1)笼子里有若干只鸡和兔,有 20 个头,有 56 只腿,那么鸡有( )只。 A.12 B.8 C.14 (2)琳琳有 2 角和 5 角的人民币共 20 张,币值总额为 5.8 元。其中 2 角的人民币有( )张。 A.6 B.14 C.29 (3)学校有象棋、跳棋共 26 副,2 人下一副象棋,6 人下一副跳棋,恰巧可供 108 人同时进行活 动。象棋有( )副。 A.12 B.14 C.16 (4)刘老师带 51 名学生去划船,共租了 10 条船。每条大船坐 6 人,每条小船坐 4 人。他们租了 ( )条大船,( )条小船。 A.4 B.5 C.6 3 乌龟和鹤共有 100 个头,共有 350 条腿,乌龟和鹤各有多少只?(导学号 99812167) 4 自行车和轿车共有 12 辆,共有 38 个车轮。自行车和轿车各有多少辆?(导学号 99812168) 5 现有 65 kg 油正好装了 20 个瓶子。大、小瓶子各多少个?(导学号 99812169) 6 动物园里有一群鸵鸟和一群长颈鹿,它们共有 60 只眼睛和 80 条腿。鸵鸟和长颈鹿各有多 少只?(导学号 99812170) 7 小兔子采蘑菇,晴天每天可以采 20 个,雨天每天可以采 12 个。这几天中有几天是晴天?有几 天是雨天?(导学号 99812171) 8 笼子里有若干只鸡和兔,鸡比兔少 5 只,共有 68 条腿。鸡和兔各有多少只? ( 导 学 号 99812172) 9 育红小学举办数学竞赛,共有 20 道题,每答对一道题得 5 分,不答或答错一道题扣 2 分,李慧 共得 79 分,她答对了几道题?(导学号 99812173) 第九单元评估 1.(1)30 12 解析:此题考查的是鸡和兔的腿数。1 只鸡有 2 条腿,1 只兔有 4 条腿,3 只鸡和 6 只兔共 3×2+6×4=30(条)腿,6 只兔比 6 只鸡多 6×4-6×2=12(条)腿。 (2)①14 10 5 5 2 ②28 4 2 2 5 解析:此题考查的是用“假设法”解决“鸡兔同笼”问题。 (3)6 7 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。此题数字较小,可以用列表法,也可以用 假设法。把以“元”为单位的数都统一成以“角”为单位,计算时方便。假设 13 支全是 5 角 的,那么一共有 13×5=65(角),就比 10 元(或 100 角)少了 100-65=35(角);已知 1 支 5 角的比 1 支 1 元的少 10-5=5(角),需要把其中的部分 5 角的换成 1 元的,补足 35 角,就要把其中的 35÷5=7(支)换成 1 元的。这说明 1 元的有 7 支,5 角的有 6 支。 (4)5 6 解 析 : 淘 气 : 假 设 12 道 题 都 答 对 了 , 应 该 得 12×10=120( 分 ), 可 实 际 得 了 40 分 , 少 了 120-40=80(分),已知答错一题扣 6 分,就少得 10+6=16(分),因为 80 分里面有 5 个 16 分,即答 错了 5 道题。笑笑:假设 10 道题都答对了,应该得 10×10=100(分),可实际得了 36 分,少了 100-36=64(分),已知答错一题扣 6 分,就少得 10+6=16(分),因为 64 分里面有 4 个 16 分,即答 错了 4 道题,也就是答对了 10-4=6(道)题。 2.(1)A 解析:此题考查的是“鸡兔同笼”问题。因为问题是求鸡的只数,所以假设 20 只都是兔,则应 该有 20×4=80(只)脚,但题中却只有 56 只,相差 80-56=24(只)脚,原因是把其中一部分鸡全算 成兔了,每只多算了 2 只脚,所以鸡的只数有 24÷2=12(只)。 (2)B 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。题中的 5.8 元先想成 58 角,2 角和 5 角 分别相当于“鸡兔同笼”问题中的鸡和兔。要求 2 角的有多少张,先假设 20 张全是 5 角的, 这样就有 20×5=100(角),可实际有 58 角,多了 100-58=42(角),原因是把其中一部分 2 角的全 算成了 5 角的,一张就多算了 5-2=3(角),所以 2 角的有 42÷3=14(张)。 (3)A 解析:此题是“鸡兔同笼”问题的变式题,考查的是对“鸡兔同笼”问题的掌握情况。“象棋和 跳棋共 26 副”,相当于“鸡兔同笼”问题中的鸡兔共 26 只;“恰巧可供 108 名学生同时进行 活动”,相当于有 108 只脚。要求象棋有多少副,可以假设 26 副全是跳棋,这样就有 26×6=156(人)下棋,可实际有 108 人在下棋,多了 156-108=48(人),原因是把其中一部分玩象 棋的人全算成了玩跳棋的,一副就多算了 6-2=4(人),所以象棋有 48÷4=12(副)。 (4)C A 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。“10 条船”相当于鸡兔共 10 只;“刘老 师带51名学生”说明有52个人,相当于52只脚。先假设10条船全是大船,可以坐6×10=60(人), 实际有 52 个人,多了 60-52=8(人),多的 8 人是因为把小船看作大船了,每条大船比每条小船多 坐了 2 人,因为 8 里面有 4 个 2,所以有 4 条小船,6 条大船。同理,也可以假设全是小船来解答。 3.方法一: 假设全是乌龟:100×4-350=50(条) 鹤:50÷(4-2)=25(只) 乌龟:100-25=75(只) 答:乌龟有 75 只,鹤有 25 只。 方法二: 假设全是鹤:350-100×2=150(条) 乌龟:150÷(4-2)=75(只) 鹤:100-75=25(只) 答:乌龟有 75 只,鹤有 25 只。 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。此题数量较大,用假设法较好。假设 100 只都是乌龟,则应该有 100×4=400(条)腿,可实际有 350 条腿,多了 400-350=50(条)腿,原因是 把其中的鹤全看作了乌龟,每只多了 2 条腿,因为 50 条腿里有 25 个 2 条腿,所以鹤有 25 只, 那么乌龟就有 100-25=75(只)。同理,也可以假设 100 只全是鹤来解答。 4.方法一: 假设全是轿车:12×4-38=10(个) 自行车:10÷(4-2)=5(辆) 轿车:12-5=7(辆) 答:自行车有 5 辆,轿车有 7 辆。 方法二: 假设全是自行车:38-12×2=14(个) 轿车:14÷(4-2)=7(辆) 自行车:12-7=5(辆) 答:自行车有 5 辆,轿车有 7 辆。 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。此题先假设 12 辆全是轿车,则应该有 12×4=48(个)车轮,可实际有 38 个车轮,多了 48-38=10(个),一辆轿车比一辆自行车多 4-2=2(个)车轮,多的 10 个车轮里面有 5 个 2 个车轮,即自行车有 5 辆,轿车有 7 辆。同理,也可 以假设全是自行车来解答。 5.方法一: 假设 20 个全是大瓶子:20×4-65=15(kg) 小瓶:15÷(4-1)=5(个) 大瓶:20-5=15(个) 答:大瓶子有 15 个,小瓶子有 5 个。 方法二: 假设 20 个全是小瓶子:65-20×1=45( kg)。 大瓶:45÷(4-1)=15(个) 小瓶:20-15=5(个) 答:大瓶子有 15 个,小瓶子有 5 个。 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。假设 20 个全是大瓶子,则应该能装 20×4=80(kg)油,可实际就有 65 kg 油,这样就多了 80-65=15(kg),因为把其中的小瓶全部看作 了大瓶,一个大瓶比一个小瓶多装 4-1=3(kg),则小瓶有 15÷(4-1)=5(个),大瓶有 20-5=15(个)。 同理,也可以假设全是小瓶子来解答。 6.60÷2=30(只) 方法一:假设全是长颈鹿,30×4-80=40(条) 鸵鸟:40÷(4-2)=20(只) 长颈鹿:30-20=10(只) 答:鸵鸟有 20 只,长颈鹿有 10 只。 方法二:假设全是鸵鸟,80-30×2=20(条) 长颈鹿:20÷(4-2)=10(只) 鸵鸟:30-10=20(只) 答:鸵鸟有 20 只,长颈鹿有 10 只。 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。此题是“鸡兔同笼”问题的变式题,增 加了难度,题中不知道鸵鸟和长颈鹿共有多少只,而已知有 60 只眼睛,我们知道鸵鸟和长颈鹿 都是有 2 只眼睛,所以可以先求出共有多少只,60÷2=30(只),然后用假设法来解答即可。 7.224÷14=16(天) 方法一:假设这 16 天全是晴天,20×16-224=96(个) 雨天:96÷(20-12)=12(天) 晴天:16-12=4(天) 答:这几天中有 4 天是晴天,有 12 天是雨天。 方法二:假设这 16 天全是雨天,224-12×16=32(个) 晴天:32÷(20-12)=4(天) 雨天:16-4=12(天) 答:这几天中有 4 天是晴天,有 12 天是雨天。 解析:此题考查的是对“鸡兔同笼”问题的掌握情况。此题是“鸡兔同笼”问题的变式题,增 加了难度,题中不知道一共采了多少天,但是可以根据“我这几天一共采了 224 个蘑菇,平均每 天采 14 个”,求出一共采了几天,列式为 224÷14=16(天)。这 16 天相当于“鸡兔同笼”问题 中的只数,224 个蘑菇相当于腿数,“晴天每天可以采 20 个,雨天每天可以采 12 个”相当于鸡 兔的腿数。用假设法计算,假设这 16 天全是晴天,则应该采 20×16=320(个)蘑菇,可实际采了 224 个,多了 320-224=96(个),原因是把其中的雨天全部看作晴天来计算的,一天晴天比一天 雨天多采 20-12=8(个),因为 96 里面有 12 个 8,所以雨天有 12 天,晴天就有 4 天。同理,也可 以假设全是雨天来解答。 8.方法一: 鸡/只 0 1 2 3 4 5 6 7 8 兔/只 5 6 7 8 9 10 11 12 13 共有的腿 数/条 20 26 32 38 44 50 56 62 68 答:鸡有 8 只,兔有 13 只。 方法二: 鸡:(68-5×4)÷(2+4)=8(只) 兔:8+5=13(只) 答:鸡有 8 只,兔有 13 只。 解析:此题考查的是“鸡兔同笼”问题。此题中不知道鸡和兔共多少只,而是知道鸡比兔少 5 只,有 68 条腿,根据这两个条件用列表法比较容易找出答案。也可以根据已知条件进行推理解 答。鸡比兔少 5 只,也就是兔比鸡多 5 只,假设这 5 只兔单独放在一个笼子里,那么原来笼子里 就会减少 5×4=20(条)腿,这样,剩下的鸡和兔就会同样多,有 68-20=48(条)腿,一只鸡和一只兔 共 4+2=6(条)腿,那么这里鸡和兔各有48÷6=8(只),再把另外的 5 只兔子加上,就可以求出兔子 的总数。 9.假设所有题都做对,(20×5-79)÷(5+2)=3(道) 20-3=17(道) 答:她做对了 17 道题。 解析:此题是“鸡兔同笼”问题的变式题,主要考查的是“鸡兔同笼”问题的掌握情况。此题 用假设法来解答。假设所有题全部答对,这样就该得 20×5=100(分),可实际李慧只得了 79 分, 相差 100-79=21(分),答对一道与答错一道相差 5+2=7(分),这样答错的题有 21÷7=3(道),答对 的就有 20-3=17(道)。注意:解决此题的关键是明确做对一题和做错一题相差 5+2=7(分),而不 是 5-2=3(分)。 第七单元检测(2) 1 下面的各图形是轴对称图形吗?请画出下面轴对称图形的对称轴。 2 我会判。(对的在括号里画“ ”,错的画“✕”) (1)轴对称图形对折后两边能完全重合。 ( ) (2)平行四边形不是轴对称图形。 ( ) (3)平移只改变图形的位置,不改变图形的形状和大小。 ( ) (4)汽车在平坦的公路上行驶是平移现象,钟面上指针的运动也是平移现象。 ( ) 3 我会选。(将正确答案的序号填在括号里) (1)下列各种图形中,是轴对称图形的是( )。 (2)右图中,图①( )能得到图②,图③是图②( )得到的。 A.向右平移 5 格 B. 向右平移 4 格 C. 向下平移 4 格 D. 向上平移 4 格 (3)下列图形中,对称轴最多的是( )。 A.圆 B.等边三角形 C.正方形 (4)把一张长方形纸对折后再对折,沿着折痕所在的直线画出心形的一半,把它沿边缘线剪下 来,能剪出( )个完整的心形。 A.1 B.2 C.4 4 阴影部分占整个图形的几分之几? (1) (2) 5 画出下面轴对称图形的另一半。(导学号 99812146) 6 画出下图先向上平移 4 格,再向右平移 5 格后的图形。 7 先画出下面图形的轴对称图形,再把原图向下平移 5 格。 8 计算下面图形 A 的面积和图形 B 的周长。(导学号 99812147) 9 一块长方形的草地,长 50 m,宽 30 m。如图,草地中有两条宽 2 m 的小路,求草地的面积。 (导学号 99812148) 答案 1. 解析:此题考查的是轴对称图形的相关知识。此题主要根据轴对称图形的特征,先判断出它们 是不是轴对称图形,再画出它们的所有对称轴。 2.(1)✕ (2) 解析:这两道题考查的是轴对称图形的特征。轴对称图形沿对称轴对折,两边能完全重合,如果 是随意对折,两边就不一定能完全重合了。平行四边形对折后不能完全重合,所以不是轴对称 图形。 (3) (4)✕ 解析:这两道题考查的是平移的特点。(4)题钟面上指针的运动是旋转现象。 3.(1)A 解析:此题考查的是轴对称图形的特征。 A 是轴对称图形,沿对称轴对折之后两边能完全重合。 (2)A C 解析:此题考查的是图形的平移。平移时,一要判断好平移的方向,二要数准平移的格数。如: 先判断方向,图②在图①的右边,所以是向右平移;再数格,在图①中确定一个点,在图②中找到 它的对应点,可以数出这两个点之间的格数是 5 格,所以选 A。同理,图②向下平移 4 格得到图 ③,所以选 C。 (3)A 解析:此题考查的是对对称轴条数的判断。因为圆有无数条对称轴,所以对称轴最多的是圆。 (4)B 解析:此题考查的是轴对称图形的特征。此题可以通过动手操作选出正确答案。 4.(1) (2) ( ) 解析:此题考查的是利用平移求阴影部分占整个图形的几分之几。做题前一定要认真观察图 形中阴影部分的特征,尽量把阴影部分平移到一起,这样就可以很明显地看出它所占的份数。 平移后如下图。 (1) (2) 5. 解析:此题考查的是轴对称图形的画法。因为轴对称图形中对称点到对称轴的距离是相等的, 所以先找出所给的一半图形的各个顶点,数出每个顶点到对称轴的距离,再在对称轴的另一侧 找出各个顶点的对称点,最后把它们顺次连接起来。 6. 解析:此题考查的是平移后的图形的画法。解决此题时,先找出图中的各关键点,即 6 个顶点, 画出最终的结果。把 6 个顶点分别向上移 4 格,再向右移 5 格的点描出来,再按原图的形状将 描出的各个顶点顺次连接起来。 7. 解析:此题考查的是轴对称图形和平移后的图形的画法。本题有两个要求,首先是画出轴对称 图形,然后是把原图向下平移 5 格。画轴对称图形的方法:找出原图的各个顶点,分别数出到对 称轴的距离,再在对称轴的另一侧找出各个顶点的对称点,最后顺次把这些点连起来。画向下 平移 5 格的图形的方法:先找出原图的几个关键点,分别向下数 5 格确定它们的位置,然后按原 图的样子画出图形即可。 8.8×4=32(cm2) (9+4)×2=26(cm) 答:图形 A 的面积是 32 cm2。图形 B 的周长是 26 cm。 解析:此题考查的是利用平移求不规则图形的面积或周长。解答本题的方法是把图形或线段 平移,把不规则图形转化成规则图形,再求面积或周长。平移后如下图。 9.(50-2)×(30-2)=1344(平方米) 答:草地的面积是 1344 平方米。 解析:此题考查的是利用平移求不规则图形的面积。此题中两条小路把草地分成 4 块,利用平 移把这 4 块拼在一起,如下图,草地的长是 50-2=48(米),宽是 30-2=28(米),直接按长方形的面 积公式求出草地的面积。 第三单元检测(2) 1 我会填。 (1)用简便方法计算 264+92+36,要先算( ),这是根据( )。 (2)几个数连乘,改变它们的运算顺序,积( )。 (3)56×5×20= ×( × ) 1800÷45=1800÷ ○ (25+11)× = ×25+ ×4 169-(69+25)=169-69○25 125×88=125○ ○ 2 我会选。(将正确答案的序号填在括号里) (1)下面的算式可以用乘法结合律进行简便计算的是( )。 A.32×4×5 B.32×4+32×5 C.32×12×4 (2)下面算式中,不能用除法的性质进行简便计算的是( )。 A.18000÷25÷40 B.800÷25×4 C.6300÷6÷15 (3)下面算式中,正确运用了乘法分配律的是( )。 A.75×(2+9)=75×2+75×9 B.35×4×6=35×(4×6) C.34×99=34×100-1 (4)小马虎把 10×(4+□)错算成 4+10×□,得到的结果与正确的结果相差( )。 A.40 B.36 C.10 (5)计算 560÷35 时,正确的简便算法是( )。 A.560÷7×5 B.560÷5×7 C.560÷7÷5 3 在○里填上“>”“<”或“=”。 (1)240-(40+127)○240-40-127 (2)54×5+5○54×10 (3)125×8×24○125×32 (4)96÷6÷3○96÷(6×3) 4 我会算。 (1)口算。 25×4= 5×8+15×8= 480÷60= 12×3÷12×3= 125×8= 55×2÷5= 565-118-82= 4×13×5= (2)怎样简便就怎样计算。 516+301+284+89 125×56 567-185-(215+67) 24×15-4×15 1900÷4÷25 99×78+78 5 填表。 某书店 2016 年第一季度部分图书销售情况统计表 图书名称 一月 二月 三月 合计 《快乐作文》 164 本 185 本 136 本 《漫画书》 234 本 166 本 576 本 《故事书》 231 本 169 本 517 本 6 解决问题。(导学号 99812047) (1) (2)这本书有 168 页,还有多少页没读? (导学号 99812048) (3)这学期在 2 月 24 日开学,在 7 月 1 日放暑假。这学期一共有多少天? (导学号 99812049) (4)学校开展植树活动。 (导学号 99812050) ①三、四年级一共有多少人参加植树活动? ②你能提出一个问题并解答吗? 第三单元评估 1 我会填。 (1)用简便方法计算 264+92+36,要先算( ),这是根据( )。 (2)几个数连乘,改变它们的运算顺序,积( )。 (3)56×5×20= ×( × ) 1800÷45=1800÷ ○ (25+11)× = ×25+ ×4 169-(69+25)=169-69○25 125×88=125○ ○ 2 我会选。(将正确答案的序号填在括号里) (1)下面的算式可以用乘法结合律进行简便计算的是( )。 A.32×4×5 B.32×4+32×5 C.32×12×4 (2)下面算式中,不能用除法的性质进行简便计算的是( )。 A.18000÷25÷40 B.800÷25×4 C.6300÷6÷15 (3)下面算式中,正确运用了乘法分配律的是( )。 A.75×(2+9)=75×2+75×9 B.35×4×6=35×(4×6) C.34×99=34×100-1 (4)小马虎把 10×(4+□)错算成 4+10×□,得到的结果与正确的结果相差( )。 A.40 B.36 C.10 (5)计算 560÷35 时,正确的简便算法是( )。 A.560÷7×5 B.560÷5×7 C.560÷7÷5 3 在○里填上“>”“<”或“=”。 (1)240-(40+127)○240-40-127 (2)54×5+5○54×10 (3)125×8×24○125×32 (4)96÷6÷3○96÷(6×3) 4 我会算。 (1)口算。 25×4= 5×8+15×8= 480÷60= 12×3÷12×3= 125×8= 55×2÷5= 565-118-82= 4×13×5= (2)怎样简便就怎样计算。 516+301+284+89 125×56 567-185-(215+67) 24×15-4×15 1900÷4÷25 99×78+78 5 填表。 某书店 2016 年第一季度部分图书销售情况统计表 图书名称 一月 二月 三月 合计 《快乐作文》 164 本 185 本 136 本 《漫画书》 234 本 166 本 576 本 《故事书》 231 本 169 本 517 本 6 解决问题。(导学号 99812047) (1) (2)这本书有 168 页,还有多少页没读? (导学号 99812048) (3)这学期在 2 月 24 日开学,在 7 月 1 日放暑假。这学期一共有多少天? (导学号 99812049) (4)学校开展植树活动。 (导学号 99812050) ①三、四年级一共有多少人参加植树活动? ②你能提出一个问题并解答吗? 第四单元检测(2) 1 我会填。 (1)0.76 是由( )个 0.1 和( )个 0.01 组成的;由 4 个一、8 个十分之一和 3 个千分之一组 成的数是( );2.01 里面有( )个百分之一。 (2)一个数的百位和百分位上都是 5,个位上是最大的一位数,十分位上是 4,其余各位上都是 0, 这个数写作( ),读作( )。 (3)0.156×1000 也就是把 0.156 的小数点向( )移动( )位;( )的小数点向左移动两位 是 1.3。 (4)求 7.9845 的近似数,保留三位小数是( ),精确到十分位是( )。 (5)南京奥林匹克体育中心占地 896000 平方米。将横线上的数改写成用“万”作单位的数 是( ),把它省略万位后面的尾数是( )。 (6)一个两位小数,保留一位小数后是 4.5,这个小数最大是( ),最小是( )。 (7)56 千克=( )吨 1.2 平方千米=( )公顷 20 千米 56 米=( )千米 5240 m=5.24( ) 960 cm2=0.096( ) 7.5 t=7( )500( ) 2 我会选。(将正确答案的序号填在括号里) (1)把下面各数中的“0”去掉后,大小不变的是( )。 A.2.60 B.30.5 C.1.020 (2)下面各小数中,最大的是( )。 A.5.603 B.5.630 C.5.063 (3)0.6、0.60、0.600 这三个数( )。 A.大小相等,计数单位相同 B.大小相等,计数单位不相同 C.大小不等,计数单位也不同 (4)把一个小数先扩大到它的 10 倍,再缩小到所得数的 ,这个数的小数点应( )。 A.向右移动一位 B.向左移动一位 C.向左移动两位 (5)找出下面各题错误的原因,把相应的序号填在括号里。 ①3.598 保留两位小数是 3.6。 ( ) ②把 143990 改写成用“万”作单位的数(保留一位小数),约是 14.4。 ( ) ③把 78360010 改写成用“亿”作单位的数(保留两位小数),约是.78 亿。 ( ) A.没有用“四舍五入”法 B.精确度不对 C.改写后没有写单位名称 D.改写成用“亿”作单位的数,当亿位上没有数时,没有添“0”补足。 3 按要求改写下面各数。 (1)改写成用“万”或“亿”作单位的数。 2569000=( )万 100 万=( )亿 3.5 亿=( )万 (2)保留一位小数。 184900≈( )万 640300800≈( )亿 36105000≈( )亿 4 我会算。 (1)7.5 (2) 0.26 (3) 1.2 5□里最大能填几?(导学号 99812091) 3.5 元>3□角 1.□4 平方千米<154 公顷 0.□8 t<650 kg 5□ m<0.057 km 6 解决问题。 (1)根据某一时段外汇汇率,1美元可兑换人民币8.15元,1欧元可兑换人民币9.26元,100美元、 1000 欧元分别可兑换人民币多少元?(导学号 99812092) (2)明明一家去外婆家,路程大约有 1000 千米,耗油多少升?(导学号 99812093) (3)王老师带着三名学生乘车去看知识竞赛。一张成人票价格是 14 元,去时买票共花了多少 钱?(导学号 99812094) 姓名 刘伟 陈红 江静 身高/m 1.54 1.38 1.17 购票须知 1.50 米以上:成人票 1.20~1.50 米:半票 1.20 米以下:免票 答案 1.(1)7 6 4.803 201 解析:此题考查的是小数的数位及计数单位的相关知识。记清数位和它的计数单位就可直接 作答。如:0.1 是十分位的计数单位,0.01 是百分位的计数单位,因此 0.76 是由 7 个 0.1 和 6 个 0.01 组成的;由 4 个一、8 个十分之一和 3 个千分之一组成的数,说明 4 在个位,8 在十分位,3 在千分位,则这个数就是 4.803;2.01 里面有 2 个一和 1 个 0.01,一和 0.01 的进率是 100,所以 2.01 里面有(200+1)个 0.01。 (2)509.45 五百零九点四五 解析:此题考查的是数位和小数的读、写法。根据描述把数写在相应的数位上,这个小数就写 出来了。读数时,按小数的读法来读。 (3)右 三 130 解析:此题考查的是小数点的移动规律。0.156×1000 就是把 0.156 扩大到原来的 1000 倍,根 据小数点的移动规律需要把小数点向右移动三位;一个数的小数点向左移动两位后是 1.3,倒 推回去,把 1.3 的小数点向右移动两位后是 130。 (4)7.985 8.0 (5)89.6 万 90 万 (6)4.54 4.45 解析:这三道题主要考查的是数的改写和近似数的求法。改写成用“万”作单位的数的方法 就是在万位的右下角点上小数点,再在后面加上一个“万”字。(6)题是求小数的近似数的逆 向思维。最大的数一定比 4.5 大,最小的数一定比 4.5 小。注意:填写后一定要检验。 (7)0.056 120 20.056 km m2 t kg 解析:此题考查的是单位换算。前三题是单纯的单位换算题,换算方法:高级单位换算成低级单 位,乘进率;低级单位换算成高级单位,除以进率。后三题是单位换算的逆运用。认真观察等号 左右两边的数是如何变化的,也就是看原数是扩大了多少还是缩小了多少。明确进率后就可 以确定单位。如:5240 m=5.24( ),5240 变成 5.24,缩小到原数的 ,单位就是 km;960 cm2=0.096( ),960 变 成 了 0.096, 缩 小 到 原 数 的 , 单 位 就 是 m2;7.5t=7( )500( ),7=7,单位不变,还是 t,0.5 变成了 500,扩大了 1000 倍,单位就是 kg。 2.(1)A 解析:此题考查的是小数的性质。要求去掉“0”而大小不变,只能去掉小数末尾的“0”,去掉 其他位置的会改变小数的大小,因此选 A。 (2)B 解析:此题考查的是小数的大小比较。比较小数的大小,先比较它们的整数部分,整数相同的, 再比较十分位上的数,如果十分位上的数相同,再比较百分位上的数,依此类推。 (3)B 解析:此题考查的是小数的性质和计数单位。在 0.6 的末尾分别添上一个“0”、两个“0”就 是 0.60、0.600,它们的大小相等,但是计数单位却不同。0.6 的计数单位是 0.1,0.60 的计数单 位是 0.01,0.600 的计数单位是 0.001。 (4)B 解析:此题考查的是小数点的移动引起小数大小的变化的规律。扩大到原来的 10 倍,就是把 小数点向右移动一位,再缩小到所得数的 ,就是把小数点向左移动两位。 (5)①B ②C ③D 解析:此题考查的是数的改写和近似数的求法。根据错误找原因,提醒我们在做题时注意避免 这些错误。 3.(1)256.9 0.01 35000 (2)18.5 6.4 0.4 解析:此题考查的是数的改写及近似数的求法。(1)100 万=( )亿,解答此类题时,可用单位 换算的方法来解。把用万作单位的数换算成用亿作单位的数,是由低级单位向高级单位换算, 应 除 以 进 率 。 1 亿 =10000 万 ,100÷10000=0.01 。 同 理 ,3.5 亿 =( ) 万 , 应 乘 进 率 10000,3.5×10000=35000。(2)先把各数改写成用“万”或“亿”作单位的数,再用“四舍五 入”法保留一位小数即可。如:184900=18.49 万≈18.5 万。 4.(1)75 0.75 (2)2.6 260 (3)0.12 12 解析:此题考查的是小数点的移动引起小数大小的变化的规律。(3)题用逆推法,先用 1.2×10=12 算出中间的数,再用 12÷100=0.12 算出第一个数。 5.4 4 5 6 解析:此题考查的是单位换算和数的大小比较。方法:先统一单位名称,再比较大小,最后找出合 适的数。如:3.5 元>3□角,3.5 元=35 角,35 角>3□角,□里可以填 0、1、2、3、4,而最大的是 4。1.□4 平方千米<154 公顷,1.□4 平方千米=1□4 公顷,1□4 公顷<154 公顷,□里可以填 0、 1、2、3、4,而最大的是 4。0.□8 t<650 kg,0.□8 t=□80 kg,□80 kg<650 kg,□里可填 1、2、 3、4、5,而最大的是 5。5□m<0.057 km,0.057 km=57 m,5□m<57m,□里可以填 0、1、2、 3、4、5、6,而最大的是 6。 6.(1)8.15×100=815(元) 9.26×1000=9260(元) 答:100 美元可兑换人民币 815 元,1000 欧元可兑换人民币 9260 元。 解析:此题考查的是小数点的移动引起小数大小的变化规律在实际生活中的应用。一个数乘 100、乘 1000,就是把它的小数点向右移动两位、三位。 (2)7.8÷100×1000=78(升) 答:耗油 78 升。 解析:此题考查的是小数点的移动引起小数大小的变化规律在实际生活中的应用。先求出行 驶 1 千米的耗油量,再求行驶 1000 千米的耗油量。7.8÷100×1000,小数点先向左移动两位,再 向右移动三位。 (3)14×2+14÷2=35(元) 答:去时买票共花 35 元。 解析:此题考查的是小数的大小比较在实际生活中的应用。刘伟身高 1.54 米,大于 1.50 米,需 购成人票;陈红身高 1.38 米,在 1.20~1.50 米的范围内,购半票,即 14÷2=7(元);江静身高 1.17 米, 在 1.20 米以下,免票。还有老师也买成人票,他们一共要买 2 张成人票,一张半票。 期 中 测 试 一、1.减 除 乘 解析:此题考查的是四则运算的运算顺序。在有中括号和小括号的算式里,要先算小括号里面 的,再算中括号里面的,最后算中括号外面的。 2.(238+7560÷90)×18=5796 解析:此题考查的是括号的应用。此题要求先算除法,再算加法,就必须加上小括号,才能最后算 乘法。 3.二点三五 2 3 5 解析:此题考查的是小数的读法和小数的数位及计数单位。读小数时,整数部分按照整数的读 法来读,小数点读作“点”,小数部分的读法是按从高位到低位的顺序依次读出各数字。根据 计数单位把该数位上的数对应填空即可。 4. 12.00 0.102 解析:此题考查的是小数的性质。把一个整数改写成小数,先在个位的右下角点上小数点,再在 后面添相应个数的 0。 5. 2.001 0.99 解析:此题考查的是数位和数的大小比较。最小的三位小数是 0.001,整数部分是 2,合起来是 2.001;求小于 1 的最大两位小数是多少,此题的条件是“小于 1”,说明整数部分是 0,“最大的 两位小数”说明小数部分是 99,合起来是 0.99。 6. 2.03 6500 1.05 解析:此题考查的是单位换算。方法是:由高级单位向低级单位换算,要乘进率;由低级单位向高 级单位换算,要除以进率。注意:1 公顷=10000 平方米。 7. 100 解析:此题考查的是小数点的移动引起小数大小的变化规律。0.24 的小数点去掉后是 24,相当 于把 0.24 的小数点向右移动了两位,所以是扩大到原数的 100 倍;20.35 变成 0.02035,小数点 向左移动了三位,所以是缩小到原数的 。注意:根据小数点移动的方向确定该小数是扩大了 还是缩小了。 8. 2.54 2.51 解析:此题考查的是小数的“四舍五入”法的逆运用。此题的关键词是“四舍”和“两位小 数”,想:2.5□,百分位上的数“四舍”了,应该是小于 5 的数,所以最大是 2.54,最小是 2.51。不 能是 2.50,因为 2.50=2.5,就不是近似数了。 9.绿 解析:此题考查的是单位换算和小数的大小比较。根据题意,三根丝带等长,用去的越少,剩下的 就越多。所以从用去的 3 个数据中比较出最小的数即可。19.3 dm=1.93 m,2 m 5 cm=2.05 m,2.05>1.93>1.88,因此绿色的剩下的最长。 二、1. 解析:此题考查的是乘法分配律的逆运用。56×99+56 表示 99 个 56 加 1 个 56,和是 100 个 56,即 56×100。完整的算式应该是 56×99+56×1,这里把“×1”省略了。 2.✕ 解析:此题考查的是小数的组成。一个小数由整数部分、小数点和小数部分组成,小数部分是 比 1 小,但它还有整数部分,整数部分可以是任意自然数,如 5.23 大于 1。 3. 解析:此题考查的是乘法分配律。12×□+12×△=12×(□+△),已知□+△=10,12×(□+ △)=12×10=120。 4.✕ 解析:此题考查的是除法性质的逆运用。一个数除以两个数的积等于这个数连续除以这两个 数。470÷(47×2)=470÷47÷2=5。 5.✕ 解析:此题考查的是加法交换律。加法交换律:两个加数相加,交换加数的位置,和不变。此题虽 然和不变,但是等号两边的加数变了。 三、1.A 解析:此题考查的是观察物体。根据两个位置观察到的形状知道此物体有 3 列,两层。要搭成 这样的物体,至少要用 4 个小正方体。如下图: 2.B 解析:此题考查的是小数的大小比较和计数单位。虽然 0.03<0.30,但 0.03 和 0.30 的计数单位 都是 0.01。 3.C 解析:此题考查的是乘法分配律的逆运用。25×36=25×(40-4)=25×40-25×4,所以选 C。A 中 23×59 应该等于 23×(60-1);B 中 45×12 应该等于 45×(10+2),它把乘法分配律和乘法结合律 混淆了。 4.A 解析:此题考查的是小数的大小比较。题中关键词是“两位小数”,即 0.21~0.29,共 9 个。 5.C 解析:此题考查的是把一个数改写成用“万”作单位的数。方法是先在万位的右下角点上小 数点,再在后面加上一个“万”字。A 中的小数点位置错了,B 中没有“万”字,故选 C。 四、1.3060 230 0 0 0.45 8 53 16 解析:此题考查的是运算顺序、有关 0 的运算、减法的性质和小数点的移动规律。计算时看 清运算符号,特别是两步计算的,要考虑好先算什么,再算什么,最后计算出结果。 2. 2300-284-116 =2300-(284+116) =2300-400 =1900 3600÷25÷4 =3600÷(25×4) =3600÷100 =36 45×98 =45×100-45×2 =4500-90 =4410 27×[(263+37)÷50] =27×[300÷50] =27×6 =162 76×18+25×18-18 =18×(76+25-1) =18×100 =1800 125×32×15 =(125×8)×(4×15) =1000×60 =60000 解析:此题考查的是四则运算的运算顺序和灵活运用运算定律进行简便运算。做每一道题之 前,先观察数的特点,判断是否能够进行简便计算。如果能,想好运用什么运算定律进行简算; 如果不能,想好运算顺序再动手计算。如:45×98,观察两个数的特点,可将 98 改写成(100-2)的 形式,再计算。 五、1.(1) (2) 解析:此题考查的是观察物体。先认真观察,再判断看到的图形的形状,最后画图。 2.ABD AD 解析:此题考查的是观察物体的知识。从同一个位置观察不同的物体,看到的形状可能是相同 的,也可能是不同的。先从前面分别观察这 4 个物体,选出看到的形状相同的物体,可知相同形 状为 ;再从上面分别观察它们,选出看到的形状相同的物体,可知相同形状为 。 六、1. 500-(72+228)=200(元) 答:还剩 200 元。 解析:此题考查的是减法的性质在实际生活中的应用。求还剩多少钱,列式为 500-(72+228),72 和 228 能凑成整百数,用 500 减去它们的和比较简便。 2.方法一: 65×13+35×13 =(65+35)×13 =100×13 =1300(元) 方法二: (65+35)×13 =100×13 =1300(元) 答:共花了 1300 元。 解析:此题考查的是运用乘法分配律解决生活中的实际问题。先根据“篮球的总价+排球的总 价=共花的钱”,列式为 65×13+35×13,然后利用乘法分配律的逆运算进行简便计算。同理, 也可以根据“(一个篮球的价钱+一个排球的价钱)×13=共花的钱”,列式为(65+35)×13。 3. 50÷6=8(条)……2(人) 方案一:租 8 条大船和 1 条小船:30×8+24=264(元) 方案二:租 7 条大船和 2 条小船:30×7+24×2=258(元) 264>258 答:租 7 条大船和 2 条小船最省钱。 解析:此题考查的是租船问题。由已知条件可知,租大船每人 5 元,租小船每人 6 元,所以尽量租 大船更省钱。可实际上,我们不但要考虑租哪种船便宜,还要考虑尽量少留空位,甚至不留空 位。 4.方案一:(40×2+15)×5=475(元) 方案二:3×5=15(次) 15 次卡 450 元 475>450 答:选方案二购票合算。 解析:此题考查的是购票问题。先按不同方案算出所花钱数,花钱少的方案最合算。 5.(70×3+16)×2=452(千米) 答:从甲地到乙地全长 452 千米。 解析:此题考查的是括号在实际问题中的应用和解决问题的能力。先认真审题,找出数量间的 关系。一个关键词是“中点”而非“终点”,先求行至中点的路程即全长的一半,然后求全长。 画线段图理解: 根据上图可列式为(70×3+16)×2。 第五单元检测(2) 1 我会填。 (1)电线杆上的三角形支架是运用了三角形具有( )的特点而设计的。 (2)一个三角形中,最少有( )个锐角,最多有( )个钝角。 (3)一个等腰三角形的顶角是 50°,它的一个底角是( )°;如果它的一个底角是 50°,它的顶角 是( )°。 (4)一个直角三角形中,其中一个锐角比另一个锐角大 30°,较小的锐角是( )°。 (5)一个等边三角形,边长是 12 cm,周长是( )cm。 (6)拼成一个等腰梯形至少需要( )个相同的等边三角形。 (7)任意一个四边形的内角和是( )°。 (8)如果三角形的两条边分别长 6 cm 和 9 cm,那么第三条边的长可能是( )cm。 (限整厘米数) 2 我会判。(对的在括号里画“ ”,错的画“✕”) (1)用 3 条线段一定能围成一个三角形。 ( ) (2)一个三角形中最多有 2 个直角。 ( ) (3)等边三角形是特殊的等腰三角形。 ( ) (4)钝角三角形中两个锐角的和小于锐角三角形中任意两个角的和。 ( ) (5)三角形中最小的角是 50°,这个三角形一定是锐角三角形。 ( ) 3 我会连。 只有两个锐角,没有钝角 等边三角形 没有钝角和直角 等腰三角形 有两个角相等,有一个钝角 锐角三角形 三条边相等 直角三角形 两个角之和等于第三个角 钝角三角形 4 我会画。 (1)画出每个三角形指定底边上的高。 (2)画一个三角形,既是钝角三角形又是等腰三角形。 5 求出下面各未知角的度数。 (1) (2) 6 解决问题。 (1)一个等腰三角形的一条边长 15 厘米,另一条边长 20 厘米,那么这个三角形的周长至少是多 少厘米?(导学号 99812120) (2)在一个直角三角形中,一个锐角是另一个锐角的 4 倍,这个直角三角形的两个锐角分别是多 少度?(导学号 99812121) (3)如右图所示,小熊每天早上从家里出发,先用9分钟到200米外的小鹿家,然后和小鹿一起用 18 分钟走 400 米到学校上学。下午放学后小熊用 23 分钟走 500 米直接回家。(导学号 99812122) ①小熊从家到学校走哪条路线最近?为什么? ②小熊从上学到放学回家一共要走多少米?平均速度是多少? 答案 1.(1)稳定性 解析:此题考查的是三角形的特性。 (2)2 1 解析:此题考查的是三角形按角分类的相关知识。锐角三角形有 3 个锐角;直角三角形有 1 个 直角,2 个锐角;钝角三角形有 1 个钝角,2 个锐角。因此,1 个三角形中,最少有 2 个锐角,最多有 1 个钝角。 (3)65° 80° 解析:此题考查的是三角形的内角和与等腰三角形的特征。已知等腰三角形的顶角是 50°,根 据三角形内角和是 180°,求其一个底角的度数,列式为(180°-50°)÷2=65°;如果一个底角是 50°, 求顶角的度数,列式为 180°-50°-50°=80°。 (4)30 解析:此题考查的是三角形的内角和与直角三角形的特征。已知三角形是直角三角形,所以两 个锐角的和是 90°,又知这两个锐角相差 30°,则这两个锐角分别是 30°和 60°。 (5)36 解析:此题考查的是等边三角形的特征。等边三角形的 3 条边都相等,周长就是 3 条边的长度 和。列式为 12×3=36(cm)。 (6)3 解析:此题考查的是等边三角形的特点。如下图: (7)360 解析:此题考查的是四边形内角和的基本概念。 (8)4、5、6、7、8、9、10、11、12、13、14 解析:此题考查的是三角形三边的关系。根据三角形任意两边之和大于第三边,可知 6 cm+9 cm>第三边,即第三边的长度一定小于 15 cm。而第三边也可能是最短边,则第三边+6 cm>9 cm,因此,第三边最短也要大于 3 cm,所以第三条边在 4 cm 与 14 cm 之间。 2.(1)✕ 解析:此题考查的是三角形的三边关系。必须满足“任意两边之和大于第三边”这一条件,才 可以围成一个三角形。 (2)✕ 解析:此题考查的是三角形的内角和。此题用假设法,如果一个三角形中有 2 个直角,那么这 2 个角的和是 180°,第三个角无论是多少度,与两个直角相加的和都会超过 180°,与“一个三角 形的内角和是 180°”矛盾。因此,一个三角形中最多只能有一个直角。 (3) 解析:此题考查的是等腰三角形和等边三角形的关系。有两条边相等的三角形是等腰三角形, 当底边与两条腰相等时,就是等边三角形。所以说等边三角形是特殊的等腰三角形。 (4) 解析:此题考查的是三角形的内角和。钝角三角形中的一个钝角大于 90°小于 180°,那么另两 个锐角的和应该小于 90°;锐角三角形中每个角都小于 90°,其中任意两个锐角的和都大于 90°, 所以,钝角三角形中两个锐角的和小于锐角三角形中任意两个角的和。 (5) 解析:此题综合考查的是三角形的内角和及锐角三角形、直角三角形和钝角三角形的特征。 判断此题用假设法。假设这个三角形是直角三角形,那么第三个角是 180°-90°-50°=40°,是最 小的角,与“最小角是 50°”矛盾,因此,这个三角形不会是直角三角形;同理,假设这个三角形是 钝角三角形,一个钝角大于 90°,第三个角就小于 40°,与“最小角是 50°”矛盾,因此,这个三角 形不会是钝角三角形。所以,这个三角形一定是锐角三角形。 3. 解析:此题考查的是三角形的分类。连线时,一定要先认真思考每个三角形的特征,然后紧扣概 念进行连线。另外,还要考虑问题的全面性,有的三角形按边分是一类,而按角分又是另一类。 如:“有两个角相等,有一个钝角”,首先想到它是钝角三角形,“有两个角相等”,说明它又是 等腰三角形。又如“三条边相等”,就是等边三角形,等边三角形又是锐角三角形,它还是等腰 三角形。 4.(1) 解析:此题考查的是给三角形作高的方法。底边一定,从底边相对的顶点到底边作垂线,别忘了 标垂直符号。 (2)(画法不唯一) 解析:此题考查的是钝角三角形和等腰三角形的特征。画的过程中,一定要注意钝角的两边的 长度相等。本题画法不唯一。 5.(1)∠1=180°-90°-50°=40° ∠2=180°-55°-40°=85° 解析:此题考查的是三角形的内角和及平角的概念。先根据三角形的内角和是 180°,求出∠1 的度数。再根据∠1、∠2 和 55°角构成一个平角,可得∠2=180°-∠1-55°。 (2)∠1=180°-64°-66°=50° ∠3=180°-66°=114° ∠2=180°-114°-25°=41° 解析:此题考查的是三角形的内角和及平角的概念。先根据三角形的内角和是 180°, 求出∠1 的度数。根据图意,∠2=180°-25°-∠3,所以求出∠3 的度数是求∠2 度数的关键。∠ 3 与 66° 角 构 成 一 个 平 角 , ∠ 3=180°-66°=114°, 进 而 求 出 ∠ 2 的 度 数 , 即 ∠ 2=180°-114°-25°=41°。 6.(1)15+15+20=50(厘米) 15+20+20=55(厘米) 50 厘米<55 厘米 答:这个三角形的周长至少是 50 厘米。 解析:此题考查的是等腰三角形的特征。两条不同的边,如果一条是腰的长度,那么另一条就是 底的长度,这样就有两个不同的等腰三角形,周长也就不同。如果腰长为 15 厘米,那么底长为 20 厘 米 , 周 长 =15+15+20=50( 厘 米 ); 如 果 腰 长 为 20 厘 米 , 那 么 底 长 为 15 厘 米 , 周 长 =20+20+15=55(厘米)。再比较大小即可。 (2)(180°-90°)÷(4+1)=18° 18°×4=72° 答:这个直角三角形的两个锐角分别是 18°和 72°。 解析:此题考查的是三角形的内角和与直角三角形的特征。一个直角三角形,一定有一个角是 90°,另两个锐角的和是 90°。已知其中一个锐角是另一个锐角的 4 倍,可以把较小的锐角的度 数看作 1 份,较大的锐角的度数就是 4 份,它们的和是 5 份,也就是 90°,这样就可以求出较小的 锐角的度数,列式为 90÷(1+4)=18°,进而求出较大锐角的度数为 18°×4=72°。 (3)①小熊从家直接去学校最近,因为两点之间的所有连线中线段最短。 解析:此题考查的是两点之间线段最短。 ②200+400+500=1100(米) 1100÷(9+18+23)=22(米/分) 答:小熊从上学到放学回家一共要走 1100 米,平均速度是 22 米/分。 解析:此题考查的是三角形的周长和速度的求法。小熊上、下学所走路线正好是一个三角形, 总路程就是这个三角形的周长,即 200+400+500=1100(米)。根据“路程÷时间=速度”,便可 以求出速度,即 1100÷(9+18+23)=22(米/分)。 注意速度的表示方法。 第一单元检测(2) 1 我会填。 (1)42+42+42+42=( )×( )=( ) (2)根据 612+129=741,写出另外两个算式:( )、( )。根据 45×21=945,写出另外两个算式:( )、( )。 (3)计算 23+(27-19)×15 时,应先算( ),再算( ),最后算( ),计算结果是 ( )。 (4)一艘宇宙飞船 5 秒钟飞行 60 千米。根据这一数据填写下表。 时间/秒 3 15 路程/千米 132 720 (5)把下面每组中的 3 个算式改写成一个综合算式。 ① 12+4=16 16÷2=8 48÷8=6 ② 96-61=35 560÷35=16 302+16=318 (6)用 28、3、84 分别写出一个乘法算式和一个除法算式:( )、( )。 2 我会判。(对的在括号里画“ ”,错的画“✕”) (1)234-70+46 与 234-(70+46)的得数相等。 ( ) (2)7+6-7+6=0 ( ) (3)在算式中,括号有改变运算顺序的作用。 ( ) (4)(300-12)×(17-13),去掉括号后,结果不变。 ( ) (5)120+▲>120 ( ) 3 我会选。(将正确答案的序号填在括号里) (1)下面算式中,结果不是 0 的是( )。 A.0+25 B.25-(12+13) C.0×25 D.0÷25 (2)下面的运算顺序与其他选项不同的一个算式是( )。 A.2×12÷3 B.15+12-3 C.12+15÷3 D.36÷3×2 (3)4×(□-25)=56,□里应填( )。 A.39 B.30 C.36 D.40 (4)170 减去 8 与 12 的积,差是( )。 A.74 B.1944 C.496 D.524 (5)( )÷( )=15……3,被除数最小是( )。 A.18 B.45 C.63 D.243 4 请你来评判。(对的在括号里画“ ”,错的画“✕”) △-○=□( ) □-○=△( ) ÷ = ( ) × = ( ) 5 我会算。 (1)直接写出得数。 23+0= 3999×0= (64-64)÷45= 720÷8+9= 0÷36= 504-504= 200×(2+5)= 25÷5+12×3= (2)计算下面各题。 540+60÷5 42+6×12-7 255-(6+13)×10 90-(80-12×5) 6 填表。 被减数 减数 差 387 152 245 102 700 120 被除数 除数 商 余数 225 17 20 13 6 478 14 30 7 解决问题。 (1)一本书有 146 页,王林已经读了 74 页,剩下的还要 6 天才能读完,王林平均每天还要读多少 页?(导学号 99812017) (2)水果店第一天上午卖出苹果 45 千克,下午比上午多卖出 8 千克,第二天卖出的数量是第一 天的 3 倍,第二天卖出多少千克苹果?(导学号 99812018) (3)同学们到出租车公司去租车,每辆可坐 30 人的大巴车,租金是 600 元;每辆可坐 20 人的中 巴车,租金是 500 元。他们怎样租车合算?(导学号 99812019) (4)动物园有两种购买门票的方案。(导学号 99812020) 方案一 成人每人 30 元 儿童每人 10 元 方案二 团体 6 人以上(包括 6 人)每人 20 元 ①如果成人 5 人,儿童 4 人,选哪种方案合算? ②如果成人 4 人,儿童 5 人,选哪种方案合算? 第一单元评估 1.(1)42 4 168 解析:此题考查的是乘法的意义,即求几个相同加数的和的简便运算。此题是求 4 个 42 相加 的和,可以列出乘法算式为 42×4。 (2)741-612=129 741-129=612 945÷45=21 945÷21=45 解析:此题考查的是加法和乘法各部分间的关系。根据“和-一个加数=另一个加数”,可以把 一个加法算式改写成两个减法算式。根据“积÷一个因数=另一个因数”,可以把一个乘法算 式改写成两个除法算式。 (3)减法 乘法 加法 143 解析:此题考查的是混合运算的运算顺序,在一个有小括号的算式里,先算小括号里面的;小括 号外面既有加法,又有乘法,应先算乘法,再算加法。 (4) 时间/秒 3 11 15 60 路程/千 米 36 132 180 720 解析:此题考查的是解决问题的能力。已知 5 秒钟飞行 60 千米,可以算出飞船的速度是每秒 飞行 12 千米,根据“速度×时间=路程”,可以知道“路程÷速度=时间”“路程÷时间=速度”, 根据公式解答即可。如第二列求时间,根据“路程÷速度=时间”,列式为 132÷12=11(秒)。 (5)①48÷[(12+4)÷2] ②302+560÷(96-61) 解析:此题考查的是列综合算式的能力和括号的实际应用。先列出综合算式,然后根据 3 个算 式的顺序调整运算顺序,需要加括号的要加括号。如第 1 组先列出 48÷12+4÷2,这个算式要先 算加法,就在 12+4 的两边加上小括号,再算除法,就需要在(12+4)÷2 的两边加中括号。注意: 列出综合算式一定要对应着题中的每一步,检查与综合算式中的运算顺序是否一致。 (6)28×3=84(或 3×28=84) 84÷3=28(或 84÷28=3) 解析:此题考查的是对乘、除法各部分间的关系的掌握情况。根据数的大小很容易列出乘法 算式 28×3=84,再列出除法算式即可。 2.(1)✕ 解析:此题考查的是运算顺序。多一个括号,计算顺序变了,结果也会不相等;也可以计算出结果 进行判断,第一个算式得 210,第二个算式得 118。 (2)✕ 解析:此题考查的是运算顺序。只含有加、减法的算式要从左往右依次计算,结果应该是 12。 (3) 解析:此题考查的是括号的作用。因为需要改变运算顺序时,就要加括号,所以括号有改变运算 顺序的作用。 (4)✕ 解析:此题考查的是括号与运算顺序的关系。分别算出结果可以证实结果会变。 (5)✕ 解析:此题考查的是 0 在计算中的特性。▲是一个未知数,最小可能是 0,如果是 0 的话,因为 120+0=120,所以 120+▲不一定大于 120。 3.(1)A 解析:此题考查的是有关 0 的运算。此题的答案很明显,因为 A 选项中 0+25=25,符合要求;而 B、C、D 选项的结果都是 0。 (2)C 解析:此题考查的是四则运算的运算顺序。A、B、D 选项中都是同一级运算,要从左往右依次 计算,只有 C 选项中同时含有两级运算,既有加法,又有除法,要先算除法,再算加法,运算顺序与 其他选项的不同。 (3)A 解析:此题考查的是 四则运算的运算顺序。 解决此题的关键是采用逆 推的方法,即 56÷4+25=39。 (4)A 解析:此题考查的是列综合算式的能力。根据题意先求积,再求差,列式为 170-8×12,计算出结 果是 74。 (5)C 解析:此题考查的是有余数除法各部分间的关系。“被除数=商×除数+余数”,而且余数要比除 数小,要想使被除数最小,除数也要最小才行,即除数最小是 4,求被除数,列式为 15×4+3=63。 4.✕ ✕ 解析:此题考查的是加法和乘法各部分间的关系。减法是加法的逆运算,根据“和-一个加数= 另一个加数”来判断两个减法算式;除法是乘法的逆运算,根据“积÷一个因数=另一个因数” 来判断乘法和除法算式。 5.(1)23 0 0 99 0 0 1400 41 解析:此题考查的是口算的能力。计算时要注意两个方面,一是有 0 的运算,二是要注意运算顺 序。 (2) 540+60÷5 =540+12 =552 42+6×12-7 =42+72-7 =114-7 =107 255-(6+13)×10 =255-19×10 =255-190 =65 90-(80-12×5) =90-(80-60) =90-20 =70 解析:此题考查的是四则混合运算的运算顺序。计算时一定要细心,注意运算顺序。如计算 540+60÷5 时,先算除法 60÷5=12,再算加法 540+12=552。 6. 被减数 减数 差 387 152 235 347 245 102 700 580 120 被除数 除数 商 余数 225 17 13 4 266 20 13 6 478 32 14 30 解析:此题考查的是减法和除法各部分间的关系。在减法中:被减数-减数=差,被减数-差=减 数,减数+差=被减数。要求什么就选对应的关系式来计算。在有余数的除法中:被除数÷除数 =商……余数,除数×商+余数=被除数,(被除数-余数)÷商=除数。如最后一行求除数时,就用 (478-30)÷14=32。 7.(1)(146-74)÷6=12(页) 答:王林平均每天还要读 12 页。 解析:此题考查的是解决问题的能力。要求平均每天还要读多少页,就要知道两个条件,一是剩 下多少页,二是要读几天。把二者找出来相除即可。 (2)方法一:[45+(45+8)]×3=294(千克) 方法二:(45+8+45)×3=294(千克) 答:第二天卖出 294 千克。 解析:此题考查的是用综合算式解决问题的能力。要求第二天卖出多少千克,就要先求出第一 天共卖出多少千克。根据关系式“上午卖出的+下午卖出的=第一天卖出的”,列式为 45+(8+45)=98(千克);再求第二天卖出的数量,列式为 98×3=294(千克)。注意括号的用法。 (3)400÷30=13(辆)……10(人) 600×12+500×2=8200(元) 答:租 12 辆大巴车,2 辆中巴车最合算。 解析:此题考查的是对租船问题的掌握情况。解决此题的关键:一是考虑租哪种车便宜;二是注 意尽量少留空座位,当有空位时,应退大换小,看看是否能减少空位量甚至没有空位。 (4)①方案一:30×5+10×4=190(元) 方案二:(5+4)×20=180(元) 190>180 答:选方案二合算。 ②方案一:30×4+10×5=170(元) 方案二:(4+5)×20=180(元) 170<180 答:选方案一合算。 解析:此题考查的是对购票问题的掌握情况。解此题时,按不同方案分别算出总票价,再进行比 较,价钱少的最合算。 第六单元检测(2) 1 我会填。 (1)在计算小数加减法时,要把( )对齐,也就是把( )对齐。得数的小数部分末尾有 0 的,一般要把 0( )。 (2)计算 65-(13.5+24.6)时,应先算( )法,再算( )法。 (3)爸爸身高 1.86 m,比妈妈高 0.27 m,妈妈身高( )m。 (4)地球表面的海洋面积约为 3.61 亿平方千米,比陆地面积多 2.12 亿平方千米,陆地面积约有 ( )亿平方千米,整个地球面积约为( )亿平方千米。 (5)3.26 至少加上( )就等于一个整数。 (6)(3.58+10.63)+1.42=10.63+( + ) 29.5-(9.5+6.42)=29.5○ ○ (7)35 连续减去 4 个 2.5,再加上 1.36,和是( )。 (8)找规律填数。 ①2.5,2.8,3.1,( ),( )。 ②10,9.3,8.6,( ),7.2,( )。 2 我会选。(对的在括号里画“ ”,错的画“✕”) (1) - 改写成小数计算是( )。 A.0.2-0.17 B.0.02-0.017 C.0.2-0.017 (2)比 5.72 小 1.36 的数再加上 0.52,和是多少?列式是( )。 A.5.72-1.36-0.52 B.5.72-1.36+0.52 C.5.72-(1.36+0.52) (3)减数是 1.5,比差少 0.32,被减数是( )。 A.1.82 B.3.32 C.2.68 (4)一个三位小数减去一个两位小数,差是( )。 A.三位小数 B.两位小数 C.一位小数 (5)0.62 扩大到原来的 10 倍后,比原数大( )。 A.6.2 B.6.82 C.5.58 3 我会算。 (1)口算。 0.36+0.05= 5.2+0.48= 1-0.56= 8.5-5.8= +0.1= 0.75-0.25= 0.1+0.01= 1-0.01= 20.9-2.8= - = (2)计算下面各题,并验算。 100-23.65= 2.56+20.4= 6.35-3.56= (3)怎样简便就怎样计算。 6.3+5.18+5.82+2.7 8.36+(8.7-2.36) 7.35-(5.2-2.65) 23.74-19.3-2.7 2.96+(5.18+2.04) 6.54-2.37+2.46-3.63 4 明明的身高是 1.35 米,他站在椅子上比爸爸高 0.17 米,椅子高多少米?(导学号 99812137) 52014 年仁川亚运会三级跳远成绩情况,如下表。(导学号 99812138) 名次 姓名 成绩/m 国籍 第一名 曹硕 17.30 中国 第二名 董斌 16.95 中国 第三名 金德现 16.93 韩国 (1)曹硕超过董斌多少米? (2)1995 年在瑞典举行的世界田径锦标赛中英国的爱德华兹创造的世界纪录为 18.29 米,至今 无人打破。曹硕的成绩离世界纪录还差多少? 6 学校买足球用了 75.8 元,比买排球多用了 45.6 元,买篮球比买排球多用了 80.8 元。买足球、 排球和篮球共用了多少元?(导学号 99812139) 答案 1.(1)小数点 相同数位 去掉 解析:此题直接考查的是小数加减法的计算方法。 (2)加 减 解析:此题考查的是小数加减混合运算的顺序。带有小括号的,要先算小括号里面的。 (3)1.59 (4)1.49 5.1 (5)0.74 解析:(3)(4)(5)题考查的是小数加减法的实际应用。(5)题的关键词是“至少”,题意是 3.26 加 上一个数等于 4,用 4-3.26 算出来即可。 (6)3.58 1.42 - 9.5 - 6.42 解析:此题考查的是加法运算定律和减法性质的应用。 (7)26.36 解析:此题考查的是小数加减混合运算。根据题意列式为 35-2.5-2.5-2.5-2.5+1.36,计算时可 以运用减法的性质,先算出 4 个 2.5 的和,使计算简便。 (8)①3.4 3.7 ②7.9 6.5 解析:此题考查的是利用小数加减法发现规律的能力。通过计算相邻两个数的差发现规律,再 填空。①题相邻两个数的差是 0.3,即后面的数比前一个数大 0.3;②题相邻的两个数差是 0.7, 即后面的数比前一个数小 0.7。 2.(1)A 解析:此题考查的是小数的计数单位。 =0.2, =0.17。 (2)B 解析:此题考查的是小数加减混合运算的应用。根据问题“和是多少”可以知道最后求和,答 案中只有 B 是最后求和的,故选 B。 (3)B 解析:此题考查的是减法各部分之间的关系。根据“被减数=差+减数”,先求差,列式为 1.5+0.32=1.82;再求被减数,列式为 1.82+1.5=3.32,故选 B。 (4)A 解析:此题考查的是小数减法的计算方法。计算小数减法时,要把小数点对齐,被减数是三位小 数,减数是两位小数,被减数的千分位上的数应直接落下来,所以差是三位小数,故选 A。 (5)C 解析:此题考查的是小数点的移动和小数减法的计算方法。这是一道易错题,0.62 扩大 10 倍 后是 6.2,求比原数大多少,也就是求 6.2 比 0.62 大多少,用减法计算。 3.(1)0.41 5.68 0.44 2.7 0.33 0.5 0.11 0.99 18.1 0.15 解析:此题考查的是简单的小数加减法的口算。计算时,注意把小数点对齐。 (2)100-23.65=76.35 . - 2 3 . 6 5 7 6 . 3 5 验算: 7 6 . 3 5 + 1 21 31 . 61 5 1 0 0 . 0� 2.56+20.4=22.96 2 . 5 6 + 2 0 . 4 2 2 . 9 6 验算: 2 2 . 9 6 - 2 0 . 4 2 . 5 6 6.35-3.56=2.79 - 3 . 5 6 2 . 7 9 验算: + 31 . 51 6 6 . 3 5 解析:此题考查的是小数加减法的计算和验算方法。小数加减法的笔算方法同整数加减法一 样,首先把小数点对齐,即相同数位对齐,从低位算起。例如,计算 100-23.65 时,100 的十分位和 百分位上没有数,要在这两个数位上用 0 占位,哪一位上不够减,要从前一位借 1 再减。 (3) 6.3+5.18+5.82+2.7 =(6.3+2.7)+(5.18+5.82) =9+11 =20 8.36+(8.7-2.36) =8.36-2.36+8.7 =6+8.7 =14.7 7.35-(5.2-2.65) =7.35-5.2+2.65 =7.35+2.65-5.2 =10-5.2 =4.8 23.74-19.3-2.7 =23.74-(19.3+2.7) =23.74-22 =1.74 2.96+(5.18+2.04) =2.96+2.04+5.18 =5+5.18 =10.18 6.54-2.37+2.46-3.63 =(6.54+2.46)-(2.37+3.63) =9-6 =3 解析:此题考查的是灵活运用加法交换律、加法结合律和减法的性质进行简算。做题之前,请 注意根据运算符号和数的特征选择合适的方法进行简算。例如,计算 6.3+5.18+5.82+2.7 时, 先观察四个加数的特点,可知运用加法交换律和加法结合律,将 6.3 和 2.7 结合到一起,5.18 和 5.82 结合到一起分别能凑成整数,即(6.3+2.7)+(5.18+5.82),会使计算简便。 4.1.82+0.17-1.35=0.64(米) 答:椅子高 0.64 米。 解析:此题考查的是解决问题的能力。由题意可知,明明站在椅子上比爸爸高 0.17 米,可列关 系式“明明的身高+椅子高度=爸爸身高+0.17 米”,根据这个关系式先求明明站在椅子上一 共有多高,列式为 1.82+0.17,再减去明明的身高,便是椅子的高度,列式为 1.82+0.17-1.35。 5.(1)17.30-16.95=0.35(米) 答:曹硕超过董斌 0.35 米。 (2)18.29-17.30=0.99(米) 答:曹硕的成绩离世界纪录还差 0.99 米。 解析:此题考查的是小数加减法的实际应用。(1)要求曹硕超过董斌多少米,就是求 17.30 比 16.95 多多少,用减法计算。(2)要求曹硕的成绩离世界纪录还差多少,就用 18.29 减去 17.30。 6.排球:75.8-45.6=30.2(元) 篮球:30.2+80.8=111(元) 一共:75.8+30.2+111=217(元) 答:买足球、排球和篮球共用了 217 元。 解析:此题考查的是小数加减法的应用。要求买足球、排球和篮球共用了多少钱,就要先求出 买排球、篮球各花了多少钱,为了避免出错,可以先分步解答,再求买这三种球共用了多少钱。 期 末 测 试 时间:90 分钟 满分:100 分 一我会填。(共 21 分,1、2 题每空 0.5 分,10 题 2 分,其他每空 1 分) 1.一个数是由 5 个十、3 个一、7 个十分之一和 2 个千分之一组成的,这个数写作( ),读 作( ),它是( )位小数。 2.5.949 保留整数是( ),保留一位小数是( ),保留两位小数是( )。 3.把 2.6 的小数点向右移动三位,再向左移动一位后是( ),相当于( )到原数的( )。 4.2.3 km=( )m 4 kg 60 g=( )kg ( )元=9 元 5 分 5.一个等腰三角形的顶角是 40°,一个底角是( )°,它还是一个( )三角形;如果它的一个 底角是 40°,顶角是( )°,它就是一个( )三角形。 6.房屋的屋架设计成三角形是运用了三角形的( )性。 7.已知被减数、减数与差的和是 220,其中减数是 30,则被减数是( ),差是( )。 8.琳琳在计算一道加法题时,把一个加数 2.3 看成了 23,算出的结果为 45.6,这道题的正确结果 是( )。 9.135600=( )万 2369590000≈( )亿(保留两位小数) 10.按从大到小的顺序排列下面各数。 5.062 50.26 5.026 52.06 50.62 二我会判。(对的在括号里画“ ”,错的画“✕”)(共 5 分) 1.三角形中任意两个角的和大于第三个角。 ( ) 2.在一个数的末尾添上两个 0,这个数就扩大到原来的 100 倍。 ( ) 3.2.□56≈3.0,□里只能填 9。 ( ) 4.如果 a÷b=3……1,那么 b×3=a+1。 ( ) 5.王强 4 次数学模拟考试的总成绩是 384 分,他每次考试成绩肯定都是 96 分。 ( ) 三我会选。(将正确答案的序号填在括号里)(共 10 分) 1.只有两个角相等的三角形一定是( )。 A.直角三角形 B.锐角三角形 C.等腰三角形 D.等边三角形 2.45×21=45×20+45 运用了( )。 A.乘法分配律 B.乘法结合律 C.乘法交换律 D.加法结合律 3.与百分位相邻的计数单位有( )。 A.十分位 B.个位 C.一 D.千分之一 4.下面四组线段,能围成三角形的是( )。 A.5 cm、5 cm、10 cm B.2 cm、2 cm、5 cm C.4 cm、6 cm、8 cm D.2 cm、10 cm、7 cm 5.给三角形画高不正确的是( )。 A. B. C. D. 四我会算。(共 25 分) 1.口算。(5 分) 1.4+4.5= 9.3-1.2= 2.5×100= 0.6÷100= 87×0+25= 5.62×100= 3.9-1.26= 2.6+3.04= 1-0.99= 1.2÷100×10= 2.用竖式计算,并验算前两道题。(8 分) 6.32+10.68= 20-10.56= 2.39+4.8= 12.13-7.6= 3.能简算的要简算。(12 分) 25×125×32 36+36×199 20-7.8-3.2 22.9+9.46-15.66 25×39 560÷[(603-253)÷50] 五求角的度数。(共 6 分) 1.(3 分) (导学号 99812189) 2.在直角三角形中,一个锐角是另一个锐角的 2 倍,较大的锐角是多少度?(3 分) ( 导 学 号 99812190) 六我会画。(共 6 分) 1.画出下面物体从不同位置看到的图形。(3 分)(导学号 99812191) 2.画出轴对称图形的另一半,并把整个图形先向上平移 3 格,再向右平移 5 格,画出平移后的图 形。(3 分)(导学号 99812192) 七解决问题。(共 27 分) 1.妈妈买了一件上衣和一条裤子,上衣每件 79.5 元,一件上衣比一条裤子便宜 5.38 元。她付给 售货员 200 元,应找回多少钱?(5 分)(导学号 99812193) 2.实验小学 5 位老师带领 100 名学生去郊游,怎样租车最省钱?(6 分)(导学号 99812194) 大客车限载 45 人,租金 300 元 小客车限载 30 人,租金 220 元 3.停车场里有轿车和六轮卡车共 25 辆,一共有 116 个轮子,轿车和六轮卡车各有多少辆?(6 分) (导学号 99812195) 4.下面是张兰和李晓的期中测试成绩统计图。(10 分)(导学号 99812196) (1)张兰和李晓的三科平均分都是 95 分,请你算出李晓的语文分和张兰的英语分。(6 分) (2)把统计图补充完整。(2 分) (3)从上面的统计图中,你能获得哪些信息?至少写两条。(2 分) 期 末 测 试 一、1.53.702 五十三点七零二 三 2.6 5.9 5.95 3.260 扩大 100 倍 4.2300 4.06 9.05 解析:这些题考查的是有关小数的知识。单位换算时,要注意两个不同单位名称之间的进率。 5.70 锐角 100 钝角 6.稳定 解析:这些题考查的是三角形的内角和、分类及其特性。等腰三角形的两腰相等,两个底角也 相等。先根据三角形的内角和是 180°和等腰三角形的特征来计算角的度数,然后判断是什么 三角形。三角形具有稳定性,房屋的屋架设计成三角形是运用了三角形的稳定性。 7.110 80 8.24.9 解析:这些题考查的是加、减法的各部分间的关系。7 题根据题意列式:被减数+减数+差=220, 利用“减数+差=被减数”,原式变为被减数+被减数=220,可知被减数=110,进而求出差是 110-30=80。8 题根据题意列式为( )+23=45.6,根据“加数=和-另一个加数”,用 45.6 减 去 23 算出另一个加数,然后与加数 2.3 相加,即可求出这道题的正确结果。列式为 45.6-23+2.3=24.9。 9.13.56 23.70 解析:此题考查的是把一个较大的数改写成用“万”或“亿”作单位的数,并按要求用“四舍 五入”法求近似数。 10.52.06>50.62>50.26>5.062>5.026 解析:此题考查的是小数的大小比较。比较小数的大小时,先比较小数的整数部分,整数部分大 的那个数就大;如果整数部分相同,就比较小数部分的十分位,十分位上的数大的那个数就大; 如果十分位上的数相同,再比较百分位上的数,依此类推,直到比较出大小为止。 二、1.✕ 解析:此题考查的是三角形的角的特点。直角三角形的两个锐角的和正好等于第三个角(直 角)。 2.✕ 解析:此题考查的是小数的性质。在小数的末尾添上两个 0,这个小数的大小不变。 3. 解析:此题考查的是“四舍五入”法的逆运用。2.□56 保留一位小数时看百分位上的数,百分 位上是 5,要向前一位进一,所以十分位上的数只能是 9 时,近似数才能是 3.0。 4.✕ 解 析 : 此 题 考 查 的 是 有 余 数 的 除 法 的 各 部 分 间 的 关 系 。 商 × 除 数 + 余 数 = 被 除 数,b×3+1=a,b×3=a-1。 5.✕ 解析:此题考查的是对平均数的意义的理解。平均分是总分除以考试次数的商,是一个平均情 况,并不是每个数的个体情况。 三、1.C 解析:此题考查的是各类三角形的特征。直角三角形和锐角三角形都不能保证有两个角相等, 而等边三角形的三个角都相等,等腰三角形的两个底角是相等的。 2.A 解析:此题考查的是乘法分配律的应用。补全过程为 45×21=45×(20+1)=45×20+45×1。 3.D 解析:此题考查的是数位顺序中数位和计数单位的区别。 4.C 解析:此题考查的是三角形的三边关系。三角形中任意两边之和大于第三边。 5.B 解析:此题考查的是三角形的高的画法。高是从三角形的顶点向对边(底)作的一条垂直线段, 这条线段的两个端点分别在底边所对的顶点和底边上。 四、1. 5.9 8.1 250 0.006 25 562 2.64 5.64 0.01 0.12 解析:此题考查的是有关小数的计算。计算时要细心,看准运算符号。 2. 6.32+10.68=17 6 . 3 2 + 1 01 . 61 8 1 7 . 0� 验算: . - 6 . 3 2 1 0 . 6 8 20-10.56=9.44 . - 1 0 . 5 6 9 . 4 4 验算: 9 . 4 4 + 11 01 . 51 6 2 0 . 0� 2.39+4.8=7.19 12.13-7.6=4.53 2 . 3 9 + 41 . 8 7 . 1 9 . - 7 . 6 4 . 5 3 解析:此题考查的是小数加、减法的竖式计算及验算。验算加法时,可以用交换两个加数的位 置来验算,也可以用“和-一个加数=另一个加数”来验算;验算减法时,用“差+减数=被减数” 来验算。 3. 25×125×32 =(25×4)×(125×8) =100×1000 =100000 36+36×199 =36×(1+199) =36×200 =7200 20-7.8-3.2 =20-(7.8+3.2) =20-11 =9 22.9+9.46-15.66 =32.36-15.66 =16.7 25×39 =25×(40-1) =25×40-25 =1000-25 =975 560÷[(603-253)÷50] =560÷[350÷50] =560÷7 =80 解析:此题考查的是简便计算。首先要判断是否能简便计算,如果能,再考虑运用什么运算定律 使计算简便;如果不能,要根据四则运算的顺序进行计算。 五、1.360°-90°×2-40°-32°=108° 答:未知角是 108°。 2.(180°-90°)÷(1+2)×2=60° 答:较大的锐角是 60°。 解析:此题考查的是三角形和四边形的内角和。1 题可以用四边形的内角和 360°减去其他几 个角,得出未知角的度数。2 题把较小的锐角看作 1 份,较大的锐角就是 2 份,由题意可知,这两 个锐角的和是 90°,先求出较小的锐角为 90÷(1+2)=30°,再求出较大的锐角为 30°×2=60°。 六、1. 解析:此题考查的是观察物体的知识。从不同位置观察同一个物体,所看到的形状是不同的。 观察时要看清一共有几个小正方形及它们的排列方式。 2. 解析:此题考查的是对轴对称和平移的理解。画轴对称图形的另一半的方法:先找到所给图形 的关键点,也就是图形的顶点;然后数出关键点到对称轴的距离,在对称轴的另一侧找到关键 点的对称点;最后按所给图形的顺序连接各点,就画出了所给图形的另一半。平移的方法:先确 定图形的几个关键点,把这几个点分别先向上平移 3 格,再向右平移 5 格后描出各个点,最后根 据原图形的形状连接各点。 七、1. 200-(79.5+5.38+79.5)=35.62(元) 答:应找回 35.62 元。 解析:此题考查的是小数加、减法在实际生活中的应用。要求应找回多少钱,就要知道花了多 少钱。上衣比裤子便宜 5.38 元,求裤子的价格列式为 79.5+5.38, 上衣和裤子一共是 79.5+5.38+79.5=164.38(元),用 200 元减去一共花的钱便是找回的钱。 2. 100+5=105(人) 105÷45=2(辆)……15(人) 300×2+220=820(元) 300+220×2=740(元) 820 元>740 元 答:租一辆大客车和 2 辆小客车最省钱。 解析:此题考查的是对“租船问题”的掌握情况。尽量租单价便宜的车,而且调整到少留空位, 甚至无空位才最省钱。 3.方法一:假设全是轿车。 25×4=100(个) 116-100=16(个) 六轮卡车:16÷2=8(辆) 轿车:25-8=17(辆) 答:轿车有 17 辆,六轮卡车有 8 辆。 方法二:假设全是六轮卡车。 25×6=150(个) 150-116=34(个) 轿车:34÷(4-2)=17(辆) 六轮卡车:25-17=8(辆) 答:轿车有 17 辆,六轮卡车有 8 辆。 解析:此题考查的是“鸡兔同笼”问题。解决此题用假设法,假设全是轿车,那么应该有 25×4=100(个)轮子,比实际轮子数量少 116-100=16(个),一辆轿车比一辆六轮卡车少 6-4=2(个)轮子,这样的话要补足这 16 个轮子需要把其中的 16÷2=8(辆)轿车变成六轮卡车, 所以六轮卡车有 8 辆,轿车有 25-8=17(辆)。同理,也可以假设全是六轮卡车来解答。 4.(1)张兰:95×3-98-91=96(分) 李晓:95×3-100-96=89(分) 答:李晓的语文成绩是 89 分,张兰的英语成绩是 96 分。 (2) (3)(答案不唯一)张兰的三科成绩中数学分数最高。李晓和张兰的英语成绩是一样的。 解析:此题考查的是平均数的逆运用和复式条形统计图的画法及分析统计图。(1)题根据平均 分求出总分,再减去其他两科的分数,便可求出第三科的分数。(2)题画条形统计图一定要看好 图例和科目。(3)题的答案不唯一,可以把能直接看到的写出来,也可以通过分析把想到的写出 来,合理即可。 期 中 测 试 时间:90 分钟 满分:100 分 一我会填。(共 20 分,每空 1 分) 1.计算 25×[(62-38)÷6]时,应先算( )法,再算( )法,最后算( )法。 2. 请 你 根 据 算 式 7560÷90=84,238+84=322 和 322×18=5796 列 出 一 道 综 合 算 式 ( )。 3.2.35 读作( ),它是由( )个一、( )个 0.1 和( )个 0.01 组成的。 4.不改变 12 的大小,把 12 改写成计数单位是 0.01 的小数是( ),把 0.10200 化简后是 ( )。 5.整数部分是 2 的最小三位小数是( ),小于 1 的最大两位小数是( )。 6.203 cm=( )m 6.5 t=( )kg 1 公顷 500 平方米=( )公顷 7.去掉 0.24 的小数点,这个数就扩大到原数的( )倍;把 20.35 缩小到原数的( )是 0.02035。 8.一个两位小数“四舍”后的近似数是 2.5,这个小数最大是( ),最小是( )。 9.同样长的三根丝带,红色的用去了 19.3 dm,绿色的用去了 1.88 m,黄色的用去了 2 m 5 cm,( )色的剩下的最长。 二我会判。(对的在括号里画“ ”,错的画“✕”)(共 5 分) 1.56×99+56=56×100 ( ) 2.小数都比 1 小。 ( ) 3.如果□+△=10,12×□+12×△=120 ( ) 4.470÷(47×2)=470÷47×2=20 ( ) 5.83+215=283+15,运用了加法交换律。 ( ) 三我会选。(将正确答案的序号填在括号里)(共 10 分) 1.一个物体,从左面看是 ,从前面看是 ,要搭成这样的物体,至少要用( )个小 正方体。 A.4 B.5 C.8 2.0.03 和 0.30 这两个小数,它们的( )。 A.大小相等,计数单位也相同 B.大小不等,计数单位相同 C.大小不等,计数单位不同 3.下列等式成立的是( )。 A.23×59=23×60-1 B.45×12=45×10×2 C.25×36=25×40-25×4 4.大于 0.2 小于 0.3 的两位小数有( )个。 A.9 B.10 C.无数个 5.中国园林博物馆是中国第一座以园林为主题的国家级博物馆,占地面积为 65000 m2。横线 上的数改写成用“万”作单位的数是( )。 A.65 万 B.6.5 C.6.5 万 四我会算。(共 28 分) 1.直接写出得数。(4 分) 102×30= 2.3×100= (58-58)÷5= 23×45×0= 45÷100= 1000÷125= 123-(23+47)= 12×4÷12×4= 2.计算下面各题,能简算的要简算。(24 分) 2300-284-116 3600÷25÷4 45×98 27×[(263+37)÷50] 76×18+25×18-18 125×32×15 五观察物体。(共 10 分) 1.画出下面物体从不同位置观察到的图形。(6 分) (1) (2) 2.(4 分) 从前面看到的形状相同的是( ),从上面看到的形状相同的是( )。 ( 导 学 号 99812095) 六解决问题。(共 27 分) 1.妈妈带了 500 元,买了一条裙子和一个包,还剩多少元?(5 分)(导学号 99812096) 2.学校买来篮球和排球各 13 个,共花了多少元?(5 分)(导学号 99812097) 3.有 50 个同学去划船,怎样租船最省钱?(5 分)(导学号 99812098) 租船须知 大船坐 6 人,租金 30 元 小船坐 4 人,租金 24 元 4.盛泰温泉有两种购票方案如下。小芳一家三口(爸爸、妈妈和小芳)去泡了 5 次,选哪种方案 购票合算?(6 分)(导学号 99812099) 方案一 成人每人每次 40 元 儿童每人每次 15 元 方案二 15 次卡 450 元 (15 次卡任何人都可以使用,不得超过 15 次) 5.一辆汽车从甲地到乙地,每小时行 70 千米,行了 3 小时距离中点还有 16 千米,从甲地到乙地 全长多少千米?(6 分)(导学号 99812100) 期 中 测 试 一、1.减 除 乘 解析:此题考查的是四则运算的运算顺序。在有中括号和小括号的算式里,要先算小括号里面 的,再算中括号里面的,最后算中括号外面的。 2.(238+7560÷90)×18=5796 解析:此题考查的是括号的应用。此题要求先算除法,再算加法,就必须加上小括号,才能最后算 乘法。 3.二点三五 2 3 5 解析:此题考查的是小数的读法和小数的数位及计数单位。读小数时,整数部分按照整数的读 法来读,小数点读作“点”,小数部分的读法是按从高位到低位的顺序依次读出各数字。根据 计数单位把该数位上的数对应填空即可。 4. 12.00 0.102 解析:此题考查的是小数的性质。把一个整数改写成小数,先在个位的右下角点上小数点,再在 后面添相应个数的 0。 5. 2.001 0.99 解析:此题考查的是数位和数的大小比较。最小的三位小数是 0.001,整数部分是 2,合起来是 2.001;求小于 1 的最大两位小数是多少,此题的条件是“小于 1”,说明整数部分是 0,“最大的 两位小数”说明小数部分是 99,合起来是 0.99。 6. 2.03 6500 1.05 解析:此题考查的是单位换算。方法是:由高级单位向低级单位换算,要乘进率;由低级单位向高 级单位换算,要除以进率。注意:1 公顷=10000 平方米。 7. 100 解析:此题考查的是小数点的移动引起小数大小的变化规律。0.24 的小数点去掉后是 24,相当 于把 0.24 的小数点向右移动了两位,所以是扩大到原数的 100 倍;20.35 变成 0.02035,小数点 向左移动了三位,所以是缩小到原数的 。注意:根据小数点移动的方向确定该小数是扩大了 还是缩小了。 8. 2.54 2.51 解析:此题考查的是小数的“四舍五入”法的逆运用。此题的关键词是“四舍”和“两位小 数”,想:2.5□,百分位上的数“四舍”了,应该是小于 5 的数,所以最大是 2.54,最小是 2.51。不 能是 2.50,因为 2.50=2.5,就不是近似数了。 9.绿 解析:此题考查的是单位换算和小数的大小比较。根据题意,三根丝带等长,用去的越少,剩下的 就越多。所以从用去的 3 个数据中比较出最小的数即可。19.3 dm=1.93 m,2 m 5 cm=2.05 m,2.05>1.93>1.88,因此绿色的剩下的最长。 二、1. 解析:此题考查的是乘法分配律的逆运用。56×99+56 表示 99 个 56 加 1 个 56,和是 100 个 56,即 56×100。完整的算式应该是 56×99+56×1,这里把“×1”省略了。 2.✕ 解析:此题考查的是小数的组成。一个小数由整数部分、小数点和小数部分组成,小数部分是 比 1 小,但它还有整数部分,整数部分可以是任意自然数,如 5.23 大于 1。 3. 解析:此题考查的是乘法分配律。12×□+12×△=12×(□+△),已知□+△=10,12×(□+ △)=12×10=120。 4.✕ 解析:此题考查的是除法性质的逆运用。一个数除以两个数的积等于这个数连续除以这两个 数。470÷(47×2)=470÷47÷2=5。 5.✕ 解析:此题考查的是加法交换律。加法交换律:两个加数相加,交换加数的位置,和不变。此题虽 然和不变,但是等号两边的加数变了。 三、1.A 解析:此题考查的是观察物体。根据两个位置观察到的形状知道此物体有 3 列,两层。要搭成 这样的物体,至少要用 4 个小正方体。如下图: 2.B 解析:此题考查的是小数的大小比较和计数单位。虽然 0.03<0.30,但 0.03 和 0.30 的计数单位 都是 0.01。 3.C 解析:此题考查的是乘法分配律的逆运用。25×36=25×(40-4)=25×40-25×4,所以选 C。A 中 23×59 应该等于 23×(60-1);B 中 45×12 应该等于 45×(10+2),它把乘法分配律和乘法结合律 混淆了。 4.A 解析:此题考查的是小数的大小比较。题中关键词是“两位小数”,即 0.21~0.29,共 9 个。 5.C 解析:此题考查的是把一个数改写成用“万”作单位的数。方法是先在万位的右下角点上小 数点,再在后面加上一个“万”字。A 中的小数点位置错了,B 中没有“万”字,故选 C。 四、1.3060 230 0 0 0.45 8 53 16 解析:此题考查的是运算顺序、有关 0 的运算、减法的性质和小数点的移动规律。计算时看 清运算符号,特别是两步计算的,要考虑好先算什么,再算什么,最后计算出结果。 2. 2300-284-116 =2300-(284+116) =2300-400 =1900 3600÷25÷4 =3600÷(25×4) =3600÷100 =36 45×98 =45×100-45×2 =4500-90 =4410 27×[(263+37)÷50] =27×[300÷50] =27×6 =162 76×18+25×18-18 =18×(76+25-1) =18×100 =1800 125×32×15 =(125×8)×(4×15) =1000×60 =60000 解析:此题考查的是四则运算的运算顺序和灵活运用运算定律进行简便运算。做每一道题之 前,先观察数的特点,判断是否能够进行简便计算。如果能,想好运用什么运算定律进行简算; 如果不能,想好运算顺序再动手计算。如:45×98,观察两个数的特点,可将 98 改写成(100-2)的 形式,再计算。 五、1.(1) (2) 解析:此题考查的是观察物体。先认真观察,再判断看到的图形的形状,最后画图。 2.ABD AD 解析:此题考查的是观察物体的知识。从同一个位置观察不同的物体,看到的形状可能是相同 的,也可能是不同的。先从前面分别观察这 4 个物体,选出看到的形状相同的物体,可知相同形 状为 ;再从上面分别观察它们,选出看到的形状相同的物体,可知相同形状为 。 六、1. 500-(72+228)=200(元) 答:还剩 200 元。 解析:此题考查的是减法的性质在实际生活中的应用。求还剩多少钱,列式为 500-(72+228),72 和 228 能凑成整百数,用 500 减去它们的和比较简便。 2.方法一: 65×13+35×13 =(65+35)×13 =100×13 =1300(元) 方法二: (65+35)×13 =100×13 =1300(元) 答:共花了 1300 元。 解析:此题考查的是运用乘法分配律解决生活中的实际问题。先根据“篮球的总价+排球的总 价=共花的钱”,列式为 65×13+35×13,然后利用乘法分配律的逆运算进行简便计算。同理, 也可以根据“(一个篮球的价钱+一个排球的价钱)×13=共花的钱”,列式为(65+35)×13。 3. 50÷6=8(条)……2(人) 方案一:租 8 条大船和 1 条小船:30×8+24=264(元) 方案二:租 7 条大船和 2 条小船:30×7+24×2=258(元) 264>258 答:租 7 条大船和 2 条小船最省钱。 解析:此题考查的是租船问题。由已知条件可知,租大船每人 5 元,租小船每人 6 元,所以尽量租 大船更省钱。可实际上,我们不但要考虑租哪种船便宜,还要考虑尽量少留空位,甚至不留空 位。 4.方案一:(40×2+15)×5=475(元) 方案二:3×5=15(次) 15 次卡 450 元 475>450 答:选方案二购票合算。 解析:此题考查的是购票问题。先按不同方案算出所花钱数,花钱少的方案最合算。 5.(70×3+16)×2=452(千米) 答:从甲地到乙地全长 452 千米。 解析:此题考查的是括号在实际问题中的应用和解决问题的能力。先认真审题,找出数量间的 关系。一个关键词是“中点”而非“终点”,先求行至中点的路程即全长的一半,然后求全长。 画线段图理解: 根据上图可列式为(70×3+16)×2。查看更多