- 2021-05-27 发布 |
- 37.5 KB |
- 3页


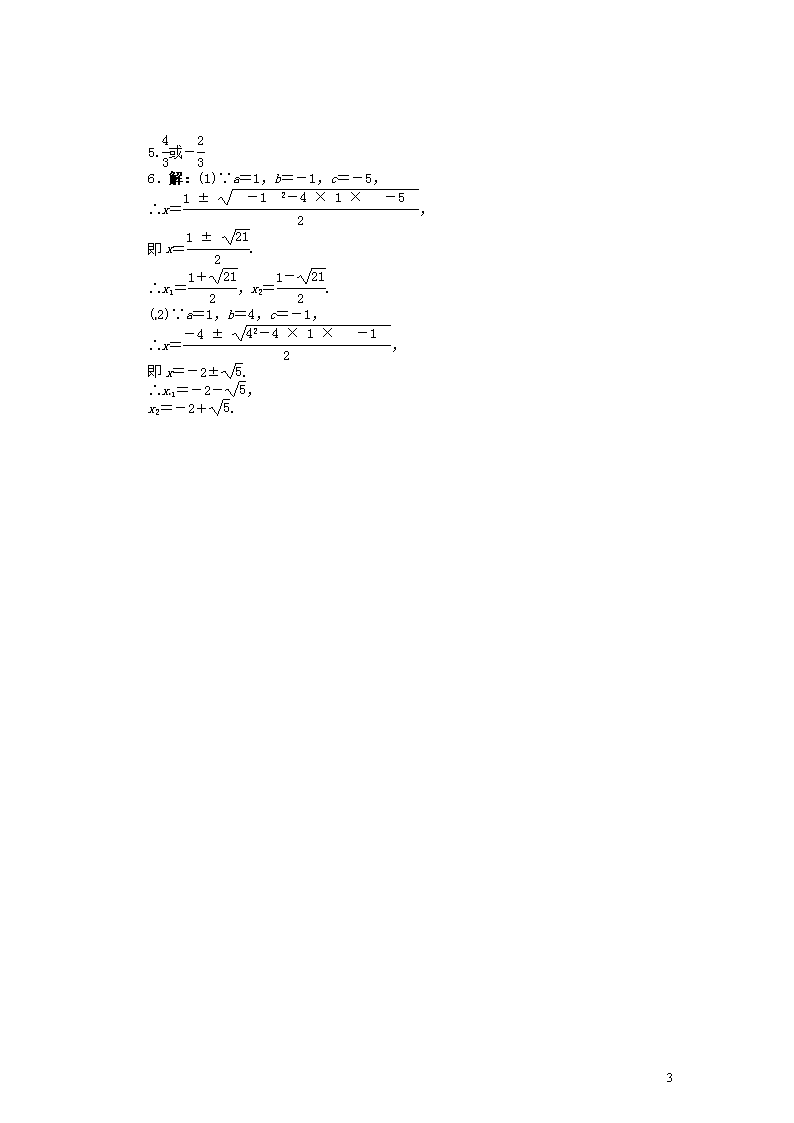
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级数学上册第22章一元二次方程22-2一元二次方程的解法第4课时学案新版华东师大版
第4课时 用公式法解一元二次方程 学前温故 用配方法解方程x2-5x=6,应把方程两边同时( ). A.加上 B.加上 C.减去 D.减去 新课早知 1.一元二次方程ax2+bx+c=0(a≠0)的求根公式是__________________. 2.用公式法解方程2x2+1=4x,下列代入公式正确的是( ). A.x= B.x= C.x= D.x= 3.方程(2x+1)(x+2)=6化成一般形式为________,b2-4ac=________,用求根公式求得x1=________,x2=________. 4.一元二次方程的解法有__________、______、______、__________,其中______和______适合于任意一元二次方程,______是最常用的方法. 5.对于方程:①x2=4;②2x2+3x=0;③x2-3x+2=0;④4x2-12x+9=0;⑤3x2=36;⑥(x-7)2=0;⑦x2=6x;⑧2x2+4x=1.把最适宜解法的序号填在下面的横线上. (1)直接开平方法____________; (2)因式分解法____________; (3)配方法____________; (4)公式法____________. 答案:学前温故 B 新课早知 1.x=(b2-4ac≥0) 2.C 3.2x2+5x-4=0 57 4.直接开平方法 配方法 公式法 因式分解法 配方法 公式法 公式法 5.(1)①⑤⑥ (2)②③④⑦ (3)⑧ (4)⑧ 用公式法解一元二次方程 【例题】 用公式法解下列方程: (1)-3x2-5x+2=0;(2)3x2+x+1=0; (3)4x2-4x+1=0;(4)4x2-3x-1=3(x-1). 3 分析:一元二次方程ax2+bx+c=0的求根公式为x=,因此只要将方程化为一般形式,确定各项系数后,代入求根公式就可以求得方程的根. 解:(1)原方程变形为3x2+5x-2=0,这里a=3,b=5,c=-2.则b2-4ac=52-4×3×(-2)=49>0, ∴x==,即x1=,x2=-2; (2)∵a=3,b=1,c=1, ∴b2-4ac=12-4×3×1=-11<0, ∴原方程无实数根; (3)∵a=4,b=-4,c=1, ∴b2-4ac=(-4)2-4×4×1=0,∴x1=x2=; (4)原方程可化为2x2-3x+1=0. ∵a=2,b=-3,c=1, ∴b2-4ac=(-3)2-4×2×1=1, ∴x=,即x1=1,x2=. 点拨:(1)运用公式法解一元二次方程时,一定要先将方程化成一般形式,再确定a、b、c的值.如果二次项系数为负数,通常把它化为正数;如果方程的系数含有分数,通常把它化为整数. (2)必须满足条件b2-4ac≥0时,才能将a、b、c及b2-4ac的值代入求根公式求解.若b2-4ac<0,则直接写原方程没有实数解;当b2-4ac=0时,这时方程的两个根相等,我们仍认为它是两个根,写成x1=x2=-,不能写成x=-. 1.(2010广西桂林中考)一元二次方程x2+3x-4=0的解是( ). A.x1=1,x2=-4 B.x1=-1,x2=4 C.x1=-1,x2=-4 D.x1=1,x2=4 2.已知4x2+4mx+36是完全平方式,则m的值为( ). A.2 B.±3 C.-6 D.±6 3.用公式法解方程x2+2x-2=0,其中a=______,b=______,c=______,b2-4ac=______,解得x1=______,x2=______. 4.把方程2x2+2m2=(4m+1)x化为关于x的一元二次方程的一般形式为__________. 5.如果x2+1与4x2-3x-5互为相反数,则x的值为__________. 6.解下列方程: (1)x2-x-5=0;(2)x2+4x-1=0. 答案:1.A 2.D 3.1 2 -2 28 -+ -- 4.2x2-(4m+1)x+2m2=0 5.或- 6.解:(1)∵a=1,b=-1,c=-5, 3 ∴x=, 即x=. ∴x1=,x2=. (2)∵a=1,b=4,c=-1, ∴x=, 即x=-2±. ∴x1=-2-, x2=-2+. 3查看更多