华师版数学九年级上册课件-第22章- 复习课

华师版数学九年级上册课件-第22章- 复习课

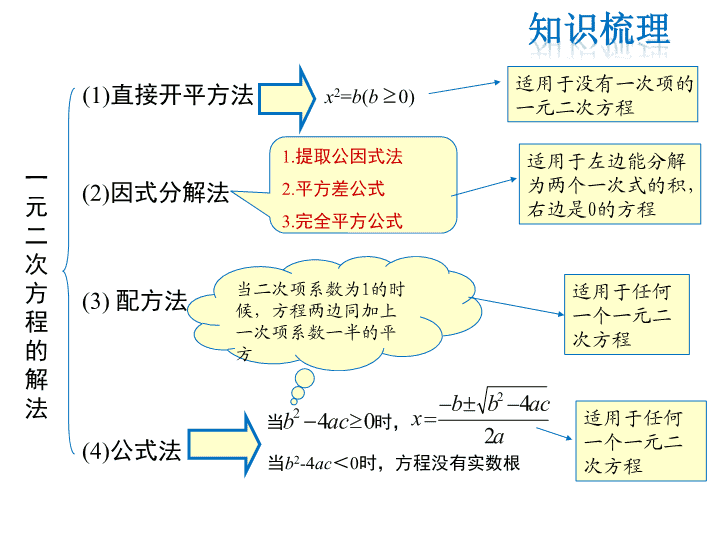
HS九(上) 教学课件 第22章 一元二次方程 复习课 本章知识结构图 实际问题 实际问题的答案 数学问题  002  acbxax a acbbx 2 42  数学问题的解 降 次 设未知数，列 方程 检 验 解 方 程 配方法 公式法 直接开平方法、 分解因式法 解一元二次方程的基本思路：将二次方程化为一次方程，即降次. 思 想 化为一 次方程 得到一元二次 方程的解 降次 解一元一次方程 (1)直接开平方法 x2=b(b 0) (2)因式分解法 1.提取公因式法 2.平方差公式 3.完全平方公式 (3) 配方法 (4)公式法 当二次项系数为1的时 候，方程两边同加上 一次项系数一半的平 方 当b2-4ac＜0时，方程没有实数根 一 元 二 次 方 程 的 解 法 适用于任何 一个一元二 次方程 适用于任何 一个一元二 次方程 适用于左边能分解 为两个一次式的积， 右边是0的方程 当 时，042  acb a acbbx 2 42  适用于没有一次项的 一元二次方程 1.若(a-3) +4x+5=0是关于x的一元二次方程，则a值为 (　　) A.3　　　B.-3　　　C.±3　　　D.无法确定 【解析】选B. 因为方程是关于x的一元二次方程，所以 a2-7=2且a-3≠0，解得a=-3. 一元二次方程及其根的有关概念 2 7ax  题型1 2.下列方程中，一定是一元二次方程的是 (　　) A.ax2+bx+c=0　 B. x2=0 C.3x2+2y- =0　 D. x2+ -5=0 【解析】选B. A中的二次项系数缺少不等于0的条件， C中含有两个未知数， D中的方程不是整式方程. 1 2 1 2 4 x 1.解方程：x2-2x-1=0. 解：移项，得x2-2x=1. 配方，得x2-2x+1=2，即(x-1)2=2. 开方，得x-1=± ，则x=1± . 所以x1=1+ , x2=1- . 2 2 2 2 一元二次方程的解法题型2 2.用适当方法解下列方程： 2( 1) 0;x   2 4 5 0;x x   25 0;x x  23 6 2 0;x x   （5） 2 23 2 4 0.x x   （1） （2） （4） (3) （直接开方法） （配方法） （因式分解法） （公式法） （因式分解法） x1=x2=1 x1=-1，x2=5 x1=0，x2= 1 5 1 2 22 5 x , x    1.若5k+20<0，则关于x的一元二次方程x2+4x-k=0的根的情 况是 (　　) A.没有实数根 B.有两个相等的实数根 C.有两个不相等的实数根 D.无法判断 【解析】选A. Δ=16+4k= (5k+20). ∵5k+20<0， ∴Δ<0，∴方程没有实数根. 4 5 根的判别式及根与系数的关系题型3 2.已知一元二次方程：①x2+2x+3=0，②x2-2x-3=0，下列说 法正确的是 (　　) A.①②都有实数解 B.①无实数解，②有实数解 C.①有实数解，②无实数解 D.①②都无实数解 【解析】选B. 一元二次方程①的判别式Δ= 4-12=-8<0，所以该方程 无实数根；一元二次方程②的判别式Δ=4+12=16>0， 所以该方程有两个不相等的实数根. 3.关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1， x2，且有x1-x1x2+x2=1-a，则a的值是 (　　) A.1　 B.-1　 C.1或-1　 D.2 【解析】选B.由题意，得 x1+x2= ，x1x2= .因为x1- x1x2+x2=1-a，所以 解得a1=1， a2=-1.当a=1时，原方程有两个相等的实数根，不合题意，舍 去，所以a=-1. 3 1a a 2 2a a 3 1 2 2 11 1        a a aa, a , a a a 即 1.某校为培养青少年科技创新能力，举办了动漫制作活动， 小明设计了点做圆周运动的一个雏型.如图所示，甲、乙两点 分别从直径的两端点A，B以顺时针、逆时针的方向同时沿圆 周运动.甲运动的路程l(cm)与时间t(s)满足关系:l= t2+ t(t≥0)， 乙以4cm/s的速度匀速运动，半圆的长度为 21cm. 1 2 3 2 一元二次方程的应用题型4 (1)甲运动4s后的路程是多少? (2)甲、乙从开始运动到第一次相遇时，它们运动了多少时间? (3)甲、乙从开始运动到第二次相遇时，它们运动了多少时间? 解：(1)当t=4时，l= ×42+ ×4=14.即甲运动4s后的路程是14cm. (2)设它们运动了ms后第一次相遇，则 +4m=21，解得 m1=3，m2=-14（舍去）.故甲、乙从开始运动到第一次相遇时， 它们运动了3s. 21 3m m 2 2      1 2 3 2 (3)设它们运动了ns后第二次相遇，则 +4n=21×3，解得 n1=7，n2=-18(舍去).故甲、乙从开始运动到第二次相遇时，它们 运动了7s. 21 3n n 2 2      2.为响应“美丽广西清洁乡村”的号召，某校开展“美丽广 西清洁校园”的活动.该校经过精心设计，计算出需要绿化的 面积为498m2，绿化150m2后，为了更快地完成该项绿化工作， 将每天的工作量提高为原来的1.2倍，结果一共用20天完成了 该项绿化工作. (1)该项绿化工作原计划每天完成多少m2? (2)在绿化工作中有一块面积为170m2的矩形场地，矩形的长 比宽的2倍少3m，这块矩形场地的长和宽各是多少米? 解：(1)设该项绿化工作原计划每天完成xm2，则提高工作 量后每天完成1.2xm2.根据题意，得 ，解得 x=22.经检验，x=22是原方程的根. 故该项绿化工作原计划每天完成22m2. (2)设矩形宽为ym，则长为(2y-3)m.根据题意，得y(2y-3)=170， 解得y=10或y=-8.5(舍去).则2y-3=17. 故这块矩形场地的长是17m，宽是10m. 150 498 150 20 1 2    x . x ★一元二次方程解应用题的基本步骤： 1.审——审清题意，找出等量关系； 2.设——直接设未知数或间接设未知数； 3.列——根据等量关系列出一元二次方程； 4.解——解方程，得出未知数的值； 5.验——既要检验是否是所列方程的解，又要检验是否符 合实际情况； 6.答——完整地写出答案，注意单位.