- 2021-05-27 发布 |
- 37.5 KB |
- 8页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020-2021学年北京市海淀区首都师大学附属中学八年级数学期中试题(图片版)
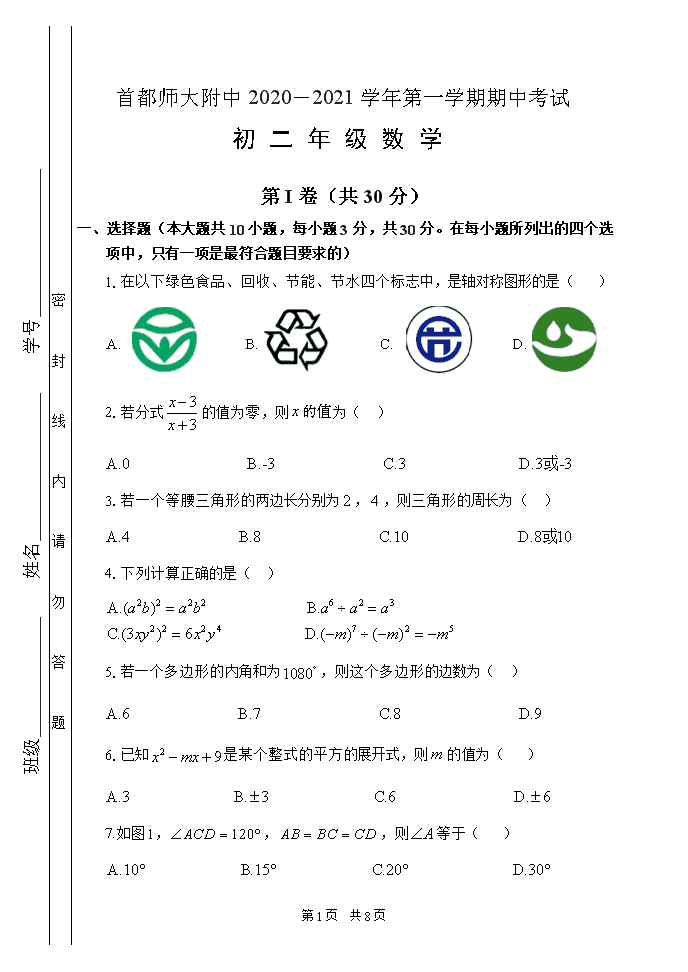
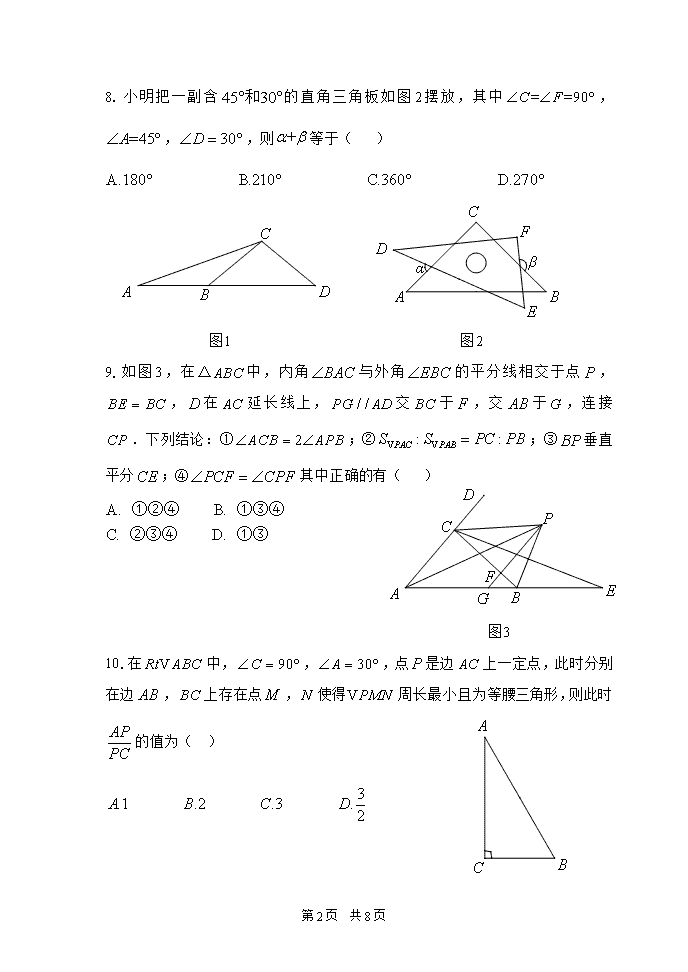
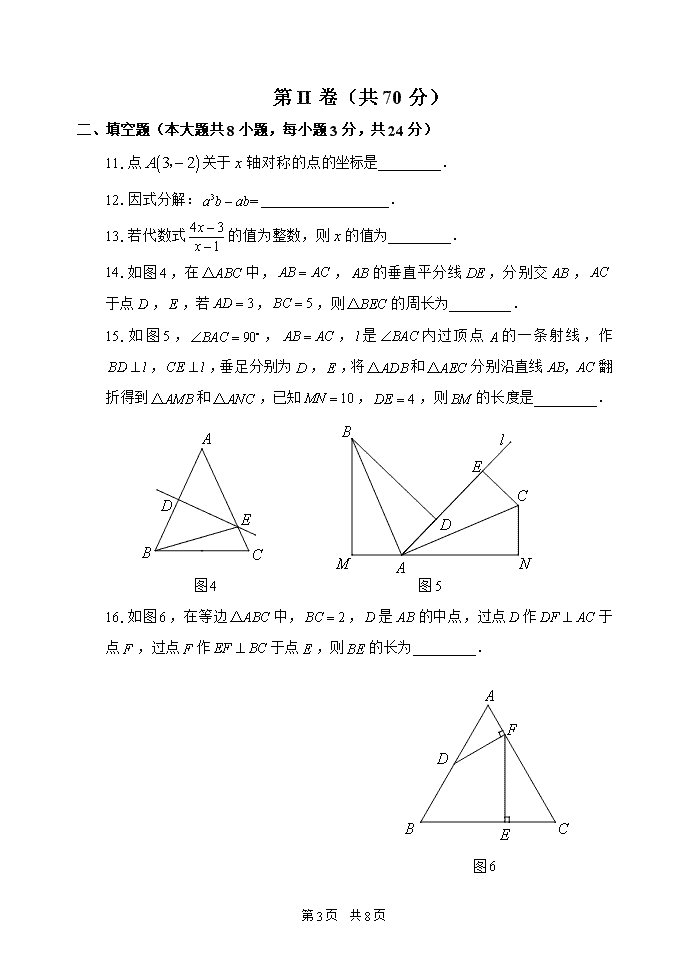
首都师大附中2020-2021学年第一学期期中考试 初二年级数学 第I卷(共30分) 一、选择题(本大题共10小题,每小题3分,共30分。在每小题所列出的四个选项中,只有一项是最符合题目要求的) 1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( ) 2.若分式的值为零,则的值为( ) 3.若一个等腰三角形的两边长分别为,,则三角形的周长为( ) 4.下列计算正确的是( ) 5.若一个多边形的内角和为,则这个多边形的边数为( ) 6.已知是某个整式的平方的展开式,则的值为( ) 7.如图,,,则等于( ) 第8页 共8页 8.小明把一副含的直角三角板如图摆放,其中,,,则等于( ) 图 图 9.如图,在中,内角与外角的平分线相交于点,,在延长线上,交于,交于,连接.下列结论:①;②;③垂直平分;④其中正确的有( ) 图 10.在中,,,点是边上一定点,此时分别在边,上存在点,使得周长最小且为等腰三角形,则此时的值为( ) 第8页 共8页 第II卷(共70分) 二、填空题(本大题共8小题,每小题3分,共24分) 11.点关于x轴对称的点的坐标是 . 12.因式分解: . 13.若代数式的值为整数,则x的值为 . 14.如图,在中,,的垂直平分线,分别交, 于点,,若,,则的周长为 . 15.如图,,,是内过顶点的一条射线,作,,垂足分别为,,将和分别沿直线翻折得到和,已知,,则的长度是 . 图 图 16.如图,在等边中,,是的中点,过点作于点,过点作于点,则的长为 . 图 第8页 共8页 17.在平面直角坐标系中,已知点,,在坐标轴上找一点,使得是等腰三角形,则这样的点共有 个. 18.请你运用所学知识找到破译的“密钥”.目前已破译出“达才”的对应口令是“成德”.根据你发现的“密钥”,破译出“求实”的对应口令是 . 自 创 厚 达 载 行 新 才 社 觉 求 天 成 实 德 坚 君 中 会 勤 奋 物 健 子 第8页 共8页 班级_____________ 姓名________________ 学号________________ 三、解答题(本大题共5小题,每小题4分,共20分) 19.计算: 20.解分式方程: 21.已知,求代数式的值. 22.先化简,再求值,其中. 23.当为何值时,关于的方程的解为负数? 四、解答题(本大题共5小题,第24-25小题,每小题4分,第26-28小题,每小题6分,共26分) 24.如图,已知等边,延长至,延长至点,使,连接,.求证:. 25.尺规作图:如图,在中 , (1)作的角平分线; (2)作边的中线. 第8页 共8页 26.若一个整数能表示成(是整数)的形式,则称这个数为“智慧数”.例如:是“智慧数”,因为;再如: (是整数),所以也是“智慧数”. (1)请你再写一个小于的“智慧数”__________,并判断是否为“智慧数”___________(填是或者否); (2)已知(是整数),是常数),要使为“智慧数”,试求出符合条件的一个值,并说明理由; (3)如果数,都是“智慧数”,试说明也是“智慧数”. 27.已知,为射线上一点,为射线上一动点,连接,满足为钝角,将线段绕点顺时针旋转,得到线段,连接. (1)依题意补全图; (2)求证:; (3)在射线上取点,点关于点的对称点为,连接,当 °时,使得对于任意的点,总有,并证明. 第8页 共8页 图 备用图 28.在平面直角坐标系中,对任意的点,定义的绝对坐标.任取点,,记,,若此时 成立,则称点相关. (1)分别判断下面各组中两点是相关点的是 ; (2)(i)对于点, 其中,其中是整数. 则所有满足条件的点有 个; (ii)求所有满足(i)条件的所有点中与点相关的点的个数; (iii)对于满足(i)条件的所有点中取出个点,满足在这个点中任意选择,两点,点,都相关,求的最大值. 第8页 共8页 草 稿 纸 第8页 共8页查看更多