【数学】2020届一轮复习北师大版数学模拟题文化课时作业

【数学】2020届一轮复习北师大版数学模拟题文化课时作业

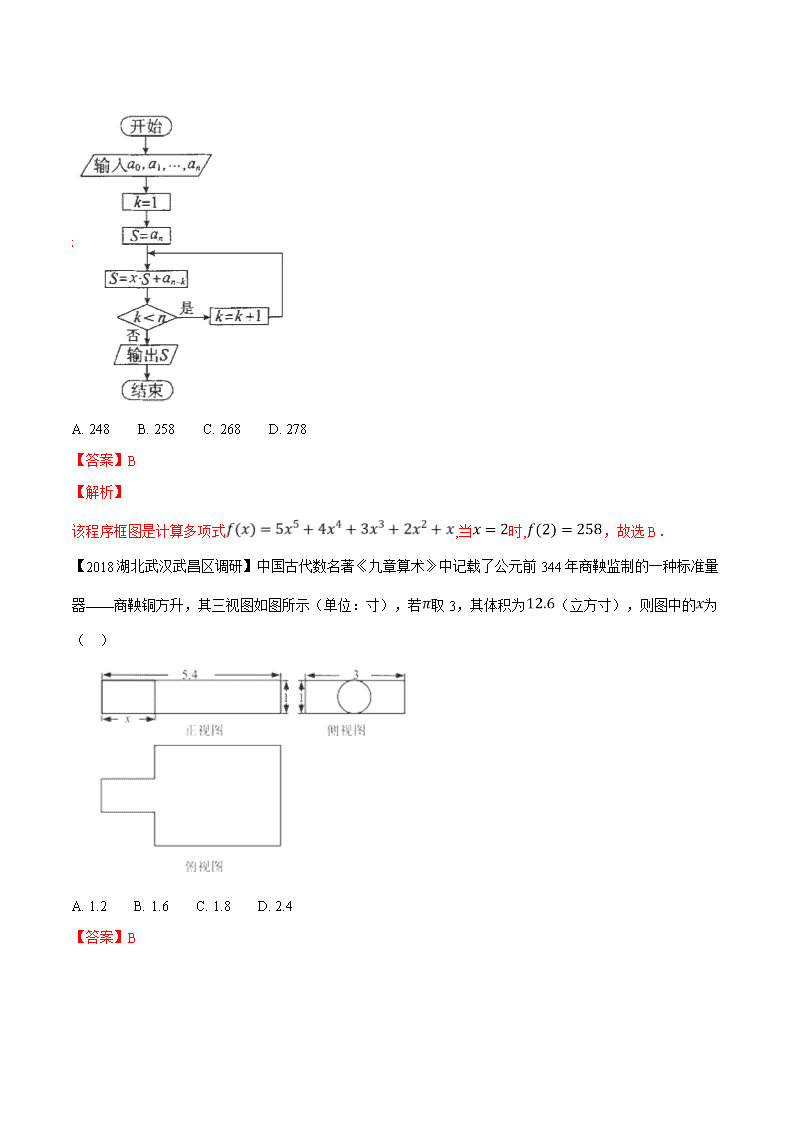
‎【备战2018高考高三数全国各地一模试卷分项精品】‎ 专题十一 数文化 一、选择题 ‎【2018安徽合肥一模】祖暅原理：“幂势既同，则积不容异”.它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面积恒相等，则体积相等，设为两个同高的几何体，的体积不相等， 在等高处的截面积不恒相等，根据祖暅原理可知，是的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【2018云南师大附中月考】秦九韶算法是南宋时期数家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，其算法的程序框图如图所示，若输入的分别为，若，根据该算法计算当时多项式的值，则输出的结果为（ ）‎ ‎【备战2018高考高三数全国各地一模试卷分项精品】‎ 专题十一 数文化 一、选择题 ‎【2018安徽合肥一模】祖暅原理：“幂势既同，则积不容异”.它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面积恒相等，则体积相等，设为两个同高的几何体，的体积不相等， 在等高处的截面积不恒相等，根据祖暅原理可知，是的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【2018云南师大附中月考】秦九韶算法是南宋时期数家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，其算法的程序框图如图所示，若输入的分别为，若，根据该算法计算当时多项式的值，则输出的结果为（ ）‎ A. 248 B. 258 C. 268 D. 278‎ ‎【答案】B ‎【解析】‎ 该程序框图是计算多项式,当时,，故选B．‎ ‎【2018湖北武汉武昌区调研】中国古代数名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升，其三视图如图所示（单位：寸），若取3，其体积为（立方寸），则图中的为（ ）‎ A. 1.2‎‎ B. 1.6 C. 1.8 D. 2.4‎ ‎【答案】B ‎【2018江西上饶一模】《九章算术》教会了人们用等差数列的知识来解决问题，《张丘建算经》卷上第22题为：“今有女善织，日益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织6尺布，现一月（按30天计）共织540尺布”，则从第2天起每天比前一天多织（ ）尺布．‎ A． B． C． D． ‎ ‎【答案】 ‎ ‎【解析】‎ 此数列为等差数列，设公差为 ，那么 ， ，解得： ，故选B.‎ ‎【2018山西五校联考】在我国明代数家吴敬所著的《九章算术比类大全》中，有一道数命题叫“宝塔装灯”，内容为“远望魏巍塔七层，红灯点点倍加增；共灯三百八十一，请问顶层几盏灯？”（“倍加增”指灯的数量从塔的顶层到底层按公比为的等比数列递增），根据此诗，可以得出塔的顶层和底层共有（ ）‎ A．盏灯 B．盏灯 C．盏灯 D．盏灯 ‎【答案】 ‎ ‎【2018‎ 广东深圳一模】祖冲之之子祖暅是我国南北朝时代伟大的家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”.意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为的平面截该几何体，则截面面积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由三视图知，这是一个底面半径为2，高为2的圆柱挖去一个底面半径为2高为2的圆锥，所以平行底面的平面截得一个圆环，其面积为两个圆面积之差，根据比例关系知截圆锥所得圆的半径为h，所以面积为，故选D．‎ 8. ‎【2018荆、荆、襄、宜四地七校联考】宋元时期数名著《算启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等.右图是源于其思想的一个程序框图，若输入的、分别为、，则输出的 ‎ A. B. C. D.‎ ‎ ‎ ‎【答案】C ‎【点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数问题，是求和还是求项.‎ 二、填空题 ‎【2018吉林二调】萨克·牛顿（‎1643年1月4日----‎1727年3月31日）英国皇家会会长，英国著名物理家，同时在数上也有许多杰出贡献，牛顿用“作切线”的方法求函数零点时给出一个数列：满足，我们把该数列称为牛顿数列.‎ 如果函数有两个零点1，2，数列为牛顿数列，设，已知，，则的通项公式__________．‎ ‎【答案】‎ ‎【解析】‎ 因为函数有两个零点1，2，所以，则，则，，即,又因为且，所以，即数列为等比数列，且通项公式为.‎ ‎【点睛】本题的思维难点在于得到后再如何进行，需要生对问题有整体性理解，与后面所给出的建立联系，即可想到要计算和的值，体现了综合法和分析法的结合.‎ ‎【2018湖北重点中联考】我国古代数著作《九章算术》中有如下问题：“今有蒲生一日，长三尺，莞生一日，长一尺。蒲生日自半。莞生日自倍。问几何日而长等？”意思是“今有蒲草第一天长高3尺，菀草第一天长高1尺。以后蒲草每天长高前一天的一半，而菀草每天长高前一天的2倍，问多少天蒲草和菀草高度相同？”根据上述已知条件，可求得第________________天，蒲草和菀草高度相同.（已知，结果精确到）‎ ‎【答案】2.6‎ ‎【2018河北衡水六调】《九章算术》是我国古代数成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积.弧田，由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长，“矢”等于半径长与圆心到弦的距离之差，按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为，弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为__________．（实际面积-弧田面积）‎ ‎【答案】‎ ‎【解析】‎ 扇形半径扇形面积等于，弧田面积圆心到弦的距离等于，所以矢长为．按照上述弧田面积经验公式计算，得．‎ ‎∴，按照弧田面积经验公式，计算结果比实际少 平方米．故答案为：．‎ ‎【2018荆、荆、襄、宜四地七校联考】“斐波那契”数列由十三世纪意大利数家斐波那契发现．数列中的一系列数字常被人们称之为神奇数．具体数列为：，即从该数列的第三项数字开始，每个数字等于前两个相邻数字之和．已知数列为“斐波那契”数列，为数列的前项和，则 ‎（Ⅰ）__________； （Ⅱ）若，则__________．（用表示）‎ ‎【答案】 （Ⅰ） （Ⅱ）