2020_2021学年新教材高中数学第二章函数章末整合课件北师大版必修第一册

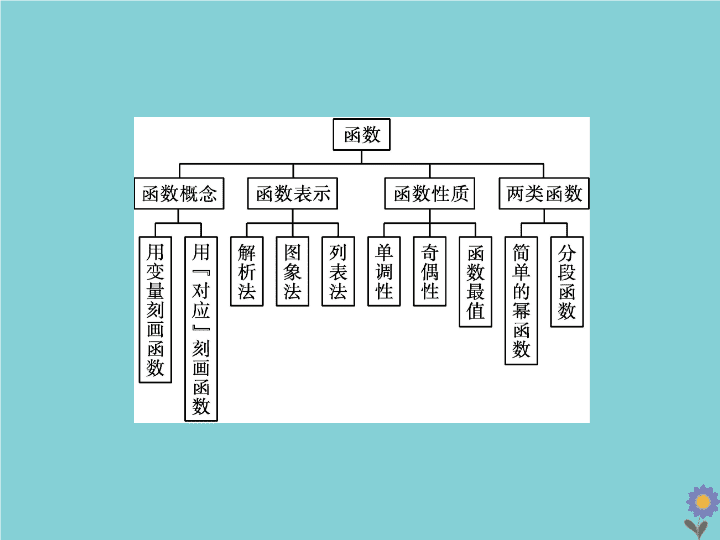
2020_2021学年新教材高中数学第二章函数章末整合课件北师大版必修第一册

章末整合 专题一 　 几种特殊函数模型的应用   1 . 二次函数 例 1 已知函数 f ( x ) =ax 2 - 2 ax+ 2 +b ( a> 0) 在区间 [2,3] 上的值域为 [2,5] . (1) 求 a , b 的值 ; (2) 若关于 x 的函数 g ( x ) =f ( x ) - ( m+ 1) x 在区间 [2,4] 上为单调函数 , 求实数 m 的取值范围 . 解 : (1) ∵ f ( x ) =a ( x- 1) 2 + 2 +b-a , 且 a> 0, ∴ 函数 f ( x ) 的图象开口向上且对称轴为直线 x= 1 . ∴ 函数 f ( x ) 在 [2,3] 上单调递增 . 方法技巧 解决二次函数在某区间上 的 单调性、值域、 最 值问题 , 关键是对函数图象的对称轴与给定区间的相对位置关系进行讨论 , 一般分为对称轴在区间的左侧、内部、右侧三种情况求解 . 变式训练 1 已知 函数 f ( x ) 是定义在 R 上的奇函数 , 当 x> 0 时 , f ( x ) =x 2 - 2 ax+a+ 2, 其中 a ∈ R . ( 1) 当 a= 1 时 , f ( - 1) = 　　　　　 ;   (2) 若 f ( x ) 的值域为 R , 则 a 的取值范围是 　　　　　 .   答案 : (1) - 2 　 (2)( -∞ , - 2] ∪ [2, +∞ ) 　 解析 : (1) 已知 a= 1, ∴ 当 x> 0 时 , f ( x ) =x 2 - 2 x+ 3 . ∵ 函数 f ( x ) 是定义在 R 上的奇函数 , ∴ f ( - 1) =-f (1) =- (1 - 2 + 3) =- 2 . (2) 由 f ( x ) 是定义在 R 上的 奇函数 , 可得 f (0) = 0 . 又当 x> 0 时 , f ( x ) 图象的对称轴为直线 x=a , ∴ 若 f ( x ) 的值域为 R , ∴ a ≥ 2 或 a ≤ - 2, 即 a 的取值范围为 ( -∞ , - 2] ∪ [2, +∞ ) . 2 . 分段 函数 取值范围是 　　　　　 .   点拨 解决有关分段函数的不等式问题的一般方法是 根据自变量 所在范围 , 及 与 之对应的函数 , 化成不含 “ f ” 的不等式求解 , 此时一般需分多种情况进行讨论 . 若给定的分段函数具有一定的单调性 , 则可利用单调性去掉符号 “ f ”, 运用这种方法求解往往比较简便 . 变式训练 2 已知函数 (1) 求实数 m 的值 ; (2) 若函数 f ( x ) 在区间 [ - 1, a- 2] 上单调递增 , 求实数 a 的取值范围 . 解 : (1) 设 x< 0, 则 -x> 0, ∴ f ( -x ) =- ( -x ) 2 + 2( -x ) =-x 2 - 2 x. ∵ f ( x ) 是奇函数 , 即 f ( -x ) =-f ( x ), ∴ 当 x< 0 时 , f ( x ) =x 2 + 2 x=x 2 +mx , ∴ m= 2 . 3 . “ 双曲 ” 函数 例 3 画出函数 y = 的 图象 , 写出函数的单调区间 , 并求出函数在 [ - 1,2] 上的值域 . 分析 用 “ 分离常数法 ” 将原函数转化成反比例函数类型 . 4 . “ 对勾 ” 函数 例 4 (2019 海南中学高一阶段检测 ) 已知函数 f ( x ) =x + , 且 f (1) = 3 . (1) 直接写出 m 的值及该函数的定义域、值域和奇偶性 ; (2) 判断函数 f ( x ) 在区间 (0, +∞ ) 上的单调性 , 并用定义证明你的结论 . (3) 图象如图所示 . 这个函数的图象形如两个对勾 , 因此 , 我们称它为 “ 对勾 ” 函数 . 专题二 　 利用函数单调性求函数的最值   (1) 判断 f ( x ) 在 [1,2] 和 [2,3] 上的单调性 ; (2) 根据 f ( x ) 的单调性写出 f ( x ) 的最值 . ∴ f ( x 1 ) >f ( x 2 ), 即 f ( x ) 在 [1,2] 上是减函数 . 当 2 ≤ x 1 0) 上最大值为 3, 最小值为 2, 求实数 a 的取值范围 . 解 : f ( x ) =x 2 - 2 x+ 3 = ( x- 1) 2 + 2 . (1) 当 0 2 . 所以 0 f (3) C. f ( - 1) =f (3) D. f (0) =f (3) (2 ) 设 f ( x ) 是定义在 R 上的奇函数 , 且 f ( x ) 的图象关于直线 x = 对称 , 则 f (1) +f (2) +f (3) +f (4) +f (5) = 　　　　 .   答案 : (1) A 　 (2)0 　 解析 : (1) 因为 f ( x+ 2) 为偶函数 , 所以其图象关于 y 轴对称 , 由于 f ( x+ 2) 的图象可由 f ( x ) 的图象向左平移 2 个单位长度得到 , 故 f ( x ) 的图象关于直线 x= 2 对称 . 因为函数 f ( x ) 在 ( -∞ ,2) 上是增函数 , 所以 f ( x ) 在 (2, +∞ ) 上 单调递增 , 所以 f ( - 1) =f (5)

查看更多