华师版数学八年级下册同步课件-第18章 平行四边形- 复习课

华师版数学八年级下册同步课件-第18章 平行四边形- 复习课

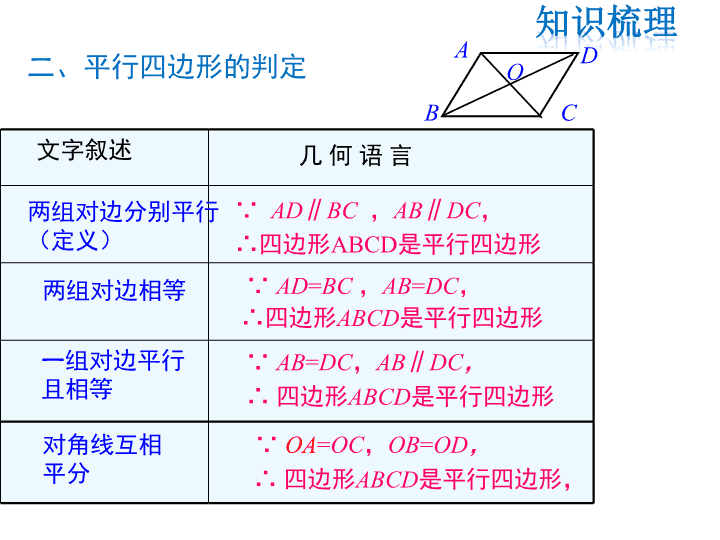
第18章 平行四边形 复习课 几 何 语 言文字叙述 对边平行 对边相等 对角相等 ∴ AD=BC ，AB=DC ∵ 四边形ABCD是平行四边形， ∴ ∠ A=∠C，∠ B=∠D ∵ 四边形ABCD是平行四边形， 一、平行四边形的性质 对角线互 相平分 ∵ 四边形ABCD是平行四边形， ∴ OA=OC，OB=OD ∵ 四边形ABCD是平行四边形， ∴ AD∥BC ，AB∥DC A B C DO 几 何 语 言文字叙述 两组对边相等 一组对边平行 且相等 ∴四边形ABCD是平行四边形 ∵ AD=BC ，AB=DC， ∴ 四边形ABCD是平行四边形 ∵ AB=DC，AB∥DC， 二、平行四边形的判定 对角线互相 平分 ∴ 四边形ABCD是平行四边形， ∵ OA=OC，OB=OD， 两组对边分别平行 （定义） ∴四边形ABCD是平行四边形 ∵ AD∥BC ，AB∥DC， A B C DO 如图，在平行四边形ABCD中，下列结论 中错误的是（　　） A．∠1=∠2 B．∠BAD=∠BCD C．AB=CD D．AC=BC D 平行四边形的性质专题1 例1 如图，在▱ ABCD中，∠ODA=90°， AC=10cm，BD=6cm，则AD的长为（　　） A．4cm B．5cm C．6cm D．8cm 解析：∵四边形ABCD是平行四边形， AC=10cm，BD=6cm， ∴OA=OC= AC=5cm，OB=OD= BD=3cm. ∵∠ODA=90°， ∴AD= =4cm． 1 2 1 2 2 2OA -OD A 例2 如图，四边形ABCD的对角线交于点O，下列哪 组条件不能判断四边形ABCD是平行四边形（　　） A．OA=OC，OB=OD B．∠BAD=∠BCD，AB∥CD C．AD∥BC，AD=BC D．AB=CD，AO=CO D 平行四边形的判定专题2 例3 如图，已知E、F分别是▱ ABCD的边BC、AD上的点， 且BE=DF．求证：四边形AECF是平行四边形． 证明：∵四边形ABCD是平行四边形， ∴AD∥BC，且AD=BC，∴AF∥EC. ∵BE=DF， ∴AF=EC， ∴四边形AECF是平行四边形． 平行四边形的性质与判定的综合应用专题3 例4 1.如图，已知▱ ABCD中，AE平分∠BAD，CF平分 ∠BCD，分别交BC、AD于点E、F． 求证：AF=EC． 证明：∵四边形ABCD是平行四边形， ∴∠B=∠D，AD=BC，AB=CD，∠BAD=∠BCD. ∵AE平分∠BAD，CF平分∠BCD， ∴∠EAB= ∠BAD，∠FCD= ∠BCD， ∴∠EAB= ∠FCD， 1 2 1 2 在△ABE和△CDF中， ∠B＝∠D， AB＝CD， ∠EAB＝∠FCD ， ∴△ABE≌△CDF，∴BE=DF． ∵AD=BC ，∴AF=EC．  解析：∵在▱ ABCD中，对角线AC和BD交于点O， AC=24cm，BD=38cm，AD=28cm， ∴CO=12cm，BO=19cm，AD=BC=28cm， ∴△BOC的周长是：BO+CO+BC=12+19+28=59(cm)． 2.如图，在▱ ABCD中，对角线AC和 BD交于点O，AC=24cm，BD=38cm， AD=28cm，则△BOC的周长是（　　） A．45cm B．59cm C．62cm D．90cm B 3.如图，点D、C在BF上，AC∥DE，∠A=∠E， BD=CF. （1）求证：AB=EF． 证明：∵AC∥DE， ∴∠ACD=∠EDF， ∵BD=CF，∴BD+DC=CF+DC， 即BC=DF. 又∵∠A=∠E，∴△ABC≌△EFD（AAS）， ∴AB=EF. （2）连结AF、BE，猜想四边形ABEF的形状，并说 明理由． 解：猜想：四边形ABEF为平行四边形. 理由如下：由（1）知△ABC≌△EFD， ∴∠ABC=∠AFE，∴AB∥EF. 又∵AB=EF， 四边形ABEF为平行四边形. 4.如图，已知凸五边形ABCDE的边长均相等，且 ∠DBE=∠ABE+∠CBD，AC=1，则BD必定满足 （　　） A．BD＜2 B．BD=2 C．BD＞2 D．以上情况均有可能 解析：∵AE=AB， ∴∠ABE=∠AEB，同理∠CBD=∠CDB. ∵∠ABE+∠CBD=∠DBE， ∴∠AEB+∠CDB=∠DBE， ∴∠AED+∠CDE=180°，∴AE∥CD. ∵AE=CD，∴四边形AEDC为平行四边形． ∴DE=AC=AB=BC． ∴△ABC是等边三角形， ∴BC=CD=1， 在△BCD中，∵BD＜BC+CD， ∴BD＜2． 故选A． 平 行 四 边 形 性质 ①对边平行且相等 ②对角相等，邻角互补 ③对角线互相平分 判定 ①两组对边分别平行的 ②两组对边分别相等的 ③一组对边平行且相等的 ④对角线互相平分的 四 边 形 平 行 四 边 形