八年级数学上册第2章三角形2-2命题与证明第3课时证明与反证法课件 湘教版

八年级数学上册第2章三角形2-2命题与证明第3课时证明与反证法课件 湘教版

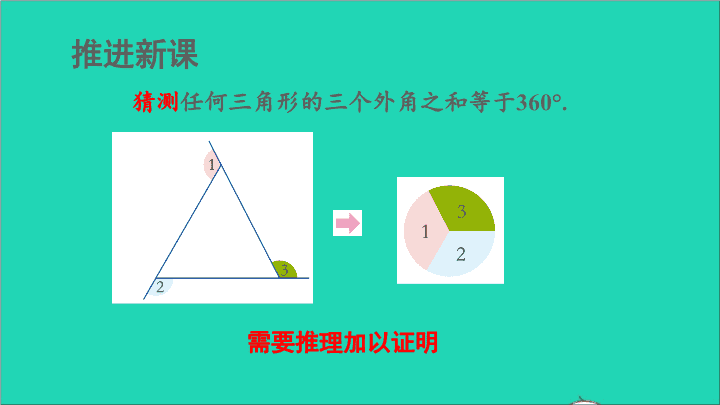
第3课时 证明与反证法 2 新课导入 观察、操作、实验是人们认识事物的重要手 段，而且人们可以从中猜测发现出一些结论. 采用剪拼或度量的方法，猜测“三角形 的外角和”等于多少度. 推进新课 猜测任何三角形的三个外角之和等于360°. 需要推理加以证明 要证明一个命题是真命题，常常要从命题的条件出 发，运用定义、基本事实以及已经证明了的定理和推论 ，通过一步步的推理，最后证实这个命题的结论成立. 证明的每一步都必须要有根据. 证明命题“三角形的外角和为360°”是真命题. 已知：如图，∠BAF，∠CBD和∠ACE分别是△ABC 的三个外角. 求证：∠BAF+∠CBD+∠ACE=360°. 证明: 如图，∵∠BAF=∠2+∠3， ∠CBD=∠1+∠3， ∠ACE=∠1+∠2（三角形外角定理）， ∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3)(等式的性质). ∵∠1+∠2+∠3=180°(三角形内角和定理)， ∴ ∠BAF+∠CBD+∠ACE=2×180°=360°. 证明与图形有关的命题时，一般有以下步骤： 第一步 画出图形根据题意 第二步 写出已知、求证根据命题的条件和结论，结合图形 第三步 写出证明的过程通过分析，找出证明的途径 已知：如图，在△ABC中，∠B=∠C，点D在线 段BA的延长线上，射线AE平分∠DAC. 求证：AE∥BC. 证明：∵∠DAC =∠B +∠C（三角形外角定理）， ∠B=∠C（已知）， ∴ ∠DAC=2∠B（等式的性质）. 又∵AE平分∠DAC（已知）， ∴∠DAC=2∠DAE（角平分线的定义）. ∴∠DAE=∠B（等量代换）. ∴AE∥BC（同位角相等，两直线平行）. 已知：∠A，∠B，∠C是△ABC的内角. 求证：∠A，∠B，∠C中至少有一个角大于或等于60°. 可能出现“有一个”、“有两个”、“有三个”这三种情况. 如果直接来证明，将很繁琐，因此， 我们将从另外一个角度来证明. 已知：∠A，∠B，∠C是△ABC的内角. 求证：∠A，∠B，∠C中至少有一个角大于或等于60°. 证明: 假设∠A，∠B，∠C 中没有一个角大于或等60°， 即∠A＜60°，∠B＜60°，∠C＜60°， 则∠A+∠B+∠C＜180°. 这与“三角形的内角和等于180°”矛盾， 所以假设不正确. 因此，∠A， ∠B， ∠C中至少有一个角大于或等于60°. 直接证明一个命题为真有困难时 假设命题不成立 利用命题的条件或有关的结论 推理 导出矛盾 假设不成立 即所证明的命题正确 反证法（间接证明）否定结论， 导出矛盾， 肯定结论 . 用反证法证明：“在△ABC中，∠A＞∠B＞∠C，则 ∠A＞60°.”第一步应假设（ ） A. ∠A＝60° B. ∠A＜60° C. ∠A ≠ 60° D. ∠A ≤ 60° D ∠A与60°的大小关系有∠A>60°，∠A=60°， ∠A<60°三种情况，因而∠A>60°的反面是∠A≤60°. 巩固练习 1. 在括号内填上理由. 已知：如图，∠A+∠B= 180°. 求证：∠C+∠D= 180°. 证明：∵∠A+∠B= 180°（已知）， ∴ AD∥BC（ ）. ∴ ∠C+∠D= 180° （ ）. 同旁内角互补，两直线平行 两直线平行，同旁内角互补 2. 已知：如图，直线AB，CD被直线MN所截，∠1=∠2. 求证：∠2=∠3，∠3+∠4=180°. 证明： ∵ ∠1=∠2， ∴ ∠2 =∠3（两直线平行,内错角相等）， ∠3+∠4=180°（两直线平行, 同旁内角互补）. ∴ AB∥CD（同位角相等，两直线平行）， 3. 已知：如图，AB与CD 相交于点E. 求证：∠A+∠C=∠B+∠D. 证明： ∵ AB与CD 相交于点E ， ∴ ∠AEC=∠BED （对顶角相等）， 又∵∠A+∠C +∠AEC =∠B+∠D +∠BED =180° （三角形内角和等于180°）， ∴ ∠A+∠C=∠B+∠D. 课后小结 命题的证明