- 2021-05-26 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
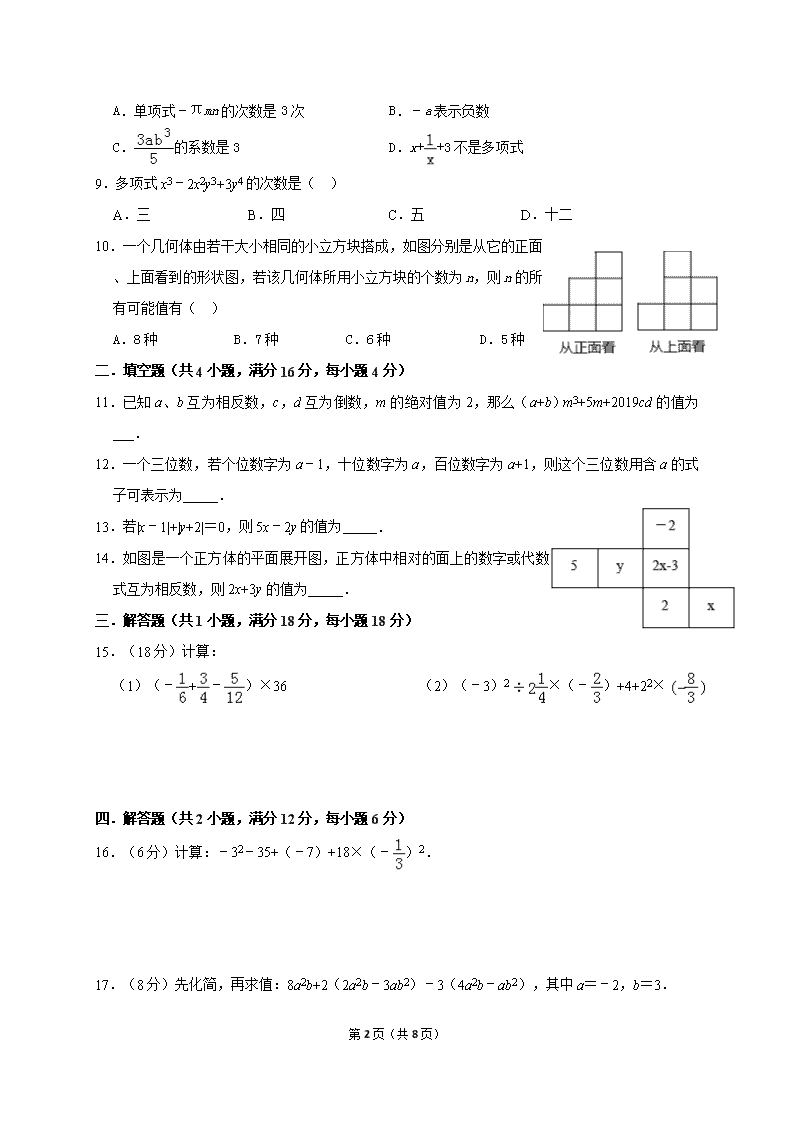
四川省成都邛崃市2019-2020学年七年级上学期期中考试数学试题
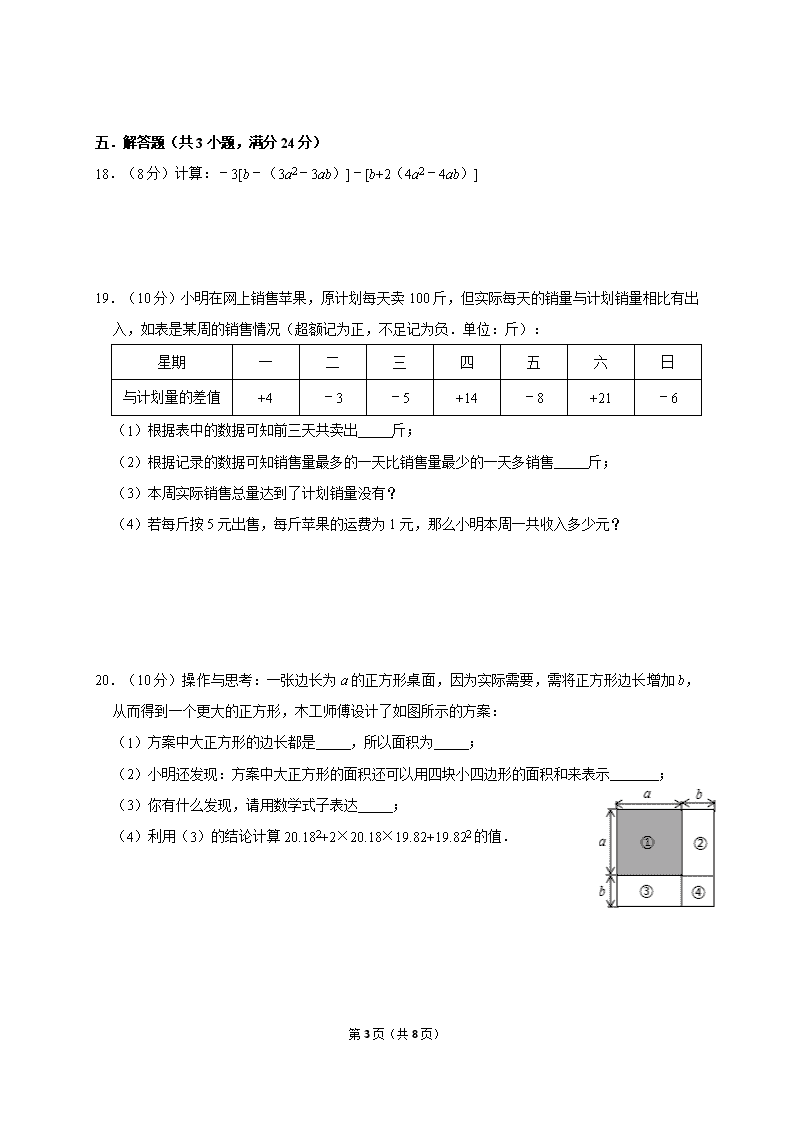
第 1页(共 8页) 2019~2020 学年度上期七年级数学半期质量监测试题 数 学 A 卷(共 100 分) 一.选择题(共 10 小题,满分 30 分,每小题 3 分) 1.﹣2 的相反数是( ) A.2 B.﹣2 C. D.﹣ 2.多项式﹣2a3b+3a2﹣4 的项数和次数分别为( ) A.3,3 B.4,3 C.3,4 D.3,6 3.已知地球上海洋面积约为 316 000 000km2,数据 316 000 000 用科学记数法可表示为( ) A.3.16×109 B.3.16×107 C.3.16×108 D.3.16×106 4.下面是小林做的 4 道作业题:(1)2ab+3ab=5ab;(2)2ab﹣3ab=﹣ab;(3)2ab﹣3ab=6ab; (4)2ab÷3ab= .做对一题得 2 分,则他共得到( ) A.2 分 B.4 分 C.6 分 D.8 分 5.如图,图(1)的正方形的周长与图(2)的长方形的周长相等,且长方形的长比宽多 acm,则正 方形的面积与长方形的面积的差为( ) A.2a2 B. a2 C. a2 D.4a2 6.代数式 的意义是( ) A.a 除以 b 与 1 的差所得的商 B.b 减 1 除 a C.b 与 1 的差除以 a D.a 除以 b 减 1 7.如图,由 5 个完全相同的小正方体组合成一个立体图形,它的左视图是( ) A. B. C. D. 8.下面的说法正确的是( ) A.单项式﹣πmn 的次数是 3 次 B.﹣a 表示负数 第 2页(共 8页) C. 的系数是 3 D.x+ +3 不是多项式 9.多项式 x3﹣2x2y3+3y4 的次数是( ) A.三 B.四 C.五 D.十二 10.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、 上面看到的形状图,若该几何体所用小立方块的个数为 n,则 n 的所有 可能值有( ) A.8 种 B.7 种 C.6 种 D.5 种 二.填空题(共 4 小题,满分 16 分,每小题 4 分) 11.已知 a、b 互为相反数,c,d 互为倒数,m 的绝对值为 2,那么(a+b)m3+5m+2019cd 的值为 . 12.一个三位数,若个位数字为 a﹣1,十位数字为 a,百位数字为 a+1,则这个三位数用含 a 的式 子可表示为 . 13.若|x﹣1|+|y+2|=0,则 5x﹣2y 的值为 . 14.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式 互为相反数,则 2x+3y 的值为 . 三.解答题(共 1 小题,满分 18 分,每小题 18 分) 15.(18 分)计算: (1)(﹣ + ﹣ )×36 (2)(﹣3)2 ×(﹣ )+4+22× 四.解答题(共 2 小题,满分 12 分,每小题 6 分) 16.(6 分)计算:﹣32﹣35+(﹣7)+18×(﹣ )2. 17.(8 分)先化简,再求值:8a2b+2(2a2b﹣3ab2)﹣3(4a2b﹣ab2),其中 a=﹣2,b=3. 五.解答题(共 3 小题,满分 24 分) 第 3页(共 8页) 18.(8 分)计算:﹣3[b﹣(3a2﹣3ab)]﹣[b+2(4a2﹣4ab)] 19.(10 分)小明在网上销售苹果,原计划每天卖 100 斤,但实际每天的销量与计划销量相比有出 入,如表是某周的销售情况(超额记为正,不足记为负.单位:斤): 星期 一 二 三 四 五 六 日 与计划量的差值 +4 ﹣3 ﹣5 +14 ﹣8 +21 ﹣6 (1)根据表中的数据可知前三天共卖出 斤; (2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤; (3)本周实际销售总量达到了计划销量没有? (4)若每斤按 5 元出售,每斤苹果的运费为 1 元,那么小明本周一共收入多少元? 20.(10 分)操作与思考:一张边长为 a 的正方形桌面,因为实际需要,需将正方形边长增加 b,从 而得到一个更大的正方形,木工师傅设计了如图所示的方案: (1)方案中大正方形的边长都是 ,所以面积为 ; (2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ; (3)你有什么发现,请用数学式子表达 ; (4)利用(3)的结论计算 20.182+2×20.18×19.82+19.822 的值. B 卷(共 100 分) 第 4页(共 8页) 一.填空题(共 5 小题,满分 20 分,每小题 4 分) 21.一个数的绝对值是 ,则这个数是 . 22.把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比 宽多 6)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为 C2,图 ③中阴影部分的周长为 C3,则 C2﹣C3= . 22 题图 23.在如图所示的运算流程中,若输出的数 y=3,则输入的数 x= . 24.若 4a+3b=1,则 8a+6b﹣3= . 25.如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小 华用其他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几 何体拼成一个无空隙的大正方体(不改变小颖所搭几何体的形状). 那么:按照小颖的要求搭几何体,小华至少需要 个正方体积木.按照小颖的要求,小华所 搭几何体的表面积最小为 . 23 题图 25 题图 二.解答题(共 3 小题,满分 30 分) 26.(8 分)某食品厂从生产的袋装食品中抽取 20 袋,检测每袋的质量是否符合标准,超过或不足 的部分分别用正、负数来表示,记录如下表: 与标准质量的差值(单位:克) ﹣5 ﹣2 0 1 3 6 袋数 1 4 3 4 5 3 (1)这批样品的质量比标准质量多还是少?多或少几克? (2)若每袋标准质量为 450 克,则抽样检测的总质量是多少? 第 5页(共 8页) 27.(10 分)将图 1 中的正方形剪开得到图 2,则图 2 中共有 4 个正方形;将图 2 中的一个正方形剪 开得到图 3,图 3 中共有 7 个正方形;将图 3 中 4 个较小的正方形中的一个剪开得到图 4,则图 4 中 共有 10 个正方形,照这个规律剪下去: (1)根据图中的规律补全表: 图形标号 1 2 3 4 5 6 正方形个数 1 4 7 10 (2)第 n 个图形中有多少个正方形? (3)当 n=673 时,图形中有多少个正方形? 28.(12 分)已知数轴上三点 A,O,B 表示的数分别为﹣3,0,1,点 P 为数轴上任意一点,其表 示的数为 x. (1)如果点 P 到点 A,点 B 的距离相等,那么 x= ; (2)当 x= 时,点 P 到点 A,点 B 的距离之和是 6; (3)若点 P 到点 A,点 B 的距离之和最小,则 x 的取值范围是 ; (4)在数轴上,点 M,N 表示的数分别为 x1,x2,我们把 x1,x2 之差的绝对值叫做点 M,N 之 间的距离,即 MN=|x1﹣x2|.若点 P 以每秒 3 个单位长度的速度从点 O 沿着数轴的负方向运动时, 点 E 以每秒 1 个单位长度的速度从点 A 沿着数轴的负方向运动、点 F 以每秒 4 个单位长度的速度 从点 B 沿着数轴的负方向运动,且三个点同时出发,那么运动 秒时,点 P 到点 E,点 F 的 距离相等. 2019~2020 学年度上期七年级数学半期质量监测试题 第 6页(共 8页) 数 学参考答案 A 卷(共 100 分) 一.选择题(共 10 小题,满分 30 分,每小题 3 分) 1. A.2. C.3. C.4. C.5. C.6. A.7. B.8. D.9. C.10.D. 二.填空题(共 4 小题,满分 16 分,每小题 4 分) 11. 2029 或 2009.12. 111a+99 13. 9.14. 1. 三.解答题(共 1 小题,满分 18 分,每小题 18 分) 15.解:(1)原式=﹣6+27﹣15=6; (2)原式=9× ×(﹣ )+4+4×(﹣ )=﹣ ﹣ +4=﹣ . 四.解答题(共 2 小题,满分 12 分,每小题 6 分) 16.解:原式=﹣9﹣35﹣7+2=﹣49. 17.解:原式=8a2b+4a2b﹣6ab2﹣12a2b+3ab2=﹣3ab2, 当 a=﹣2,b=3 时,原式=54. 五.解答题(共 3 小题,满分 24 分) 18.解:原式=﹣3b+9a2﹣9ab﹣b﹣8a2+8ab=a2﹣4b﹣ab. 19.解:(1)根据题意得:300+4﹣3﹣5=296; (2)根据题意得:321﹣292=29; 故答案为:(1)296;(2)29; (3)+4﹣3﹣5+14﹣8+21﹣6=17>0, 故本周实际销量达到了计划销量. (4)(17+100×7)×(5﹣1)=717×4=2868(元). 答:小明本周一共收入 2868 元. 20.解:(1)方案中大正方形的边长都是(a+b),所以面积为(a+b)2, 故答案为:(a+b),(a+b)2; (2)方案中大正方形的面积还可以用四块小四边形的面积和来表示:a2+ab+ab+b2=a2+2ab+b2, 故答案为:(a2+2ab+b2); (3)根据大正方形的面积不变可知(a+b)2=a2+2ab+b2, 故答案为:(a+b)2=a2+2ab+b2. 第 7页(共 8页) (4)20.182+2×20.18×19.82+19.822 =(20.18+19.82)2 =402 =1600. B 卷(共 100 分) 一.填空题(共 5 小题,满分 20 分,每小题 4 分) 21.±4 . 22. 12 23.5 或 6 24.﹣1. 25. 17,48. 二.解答题(共 3 小题,满分 30 分) 26.解:(1)根据题意得:﹣5×1﹣2×4+0×3+1×4+3×5+6×3=﹣5﹣80+4+15+18=24(克), 则这批样品的质量比标准质量多,多 24 克; (2)根据题意得:20×450+24=9024(克), 则抽样检测的总质量是 9024 克. 27.解:(1)按图示规律填写下表: 图形标号 1 2 3 4 5 6 正方形个数 1 4 7 10 13 16 故答案为 13,16; (2)第 1 个图形有正方形 1 个, 第 2 个图形有正方形 4 个, 第 3 个图形有正方形 7 个, 第 4 个图形有正方形 10 个, …, 第 n 个图形有正方形(3n﹣2)个. (3)第 673 个图中共有正方形的个数为 3×673﹣2=2017. 28.解:(1)由题意得,|x﹣(﹣3)|=|x﹣1|, 解得 x=﹣1; (2)∵AB=|1﹣(﹣3)|=4,点 P 到点 A,点 B 的距离之和是 6, ∴点 P 在点 A 的左边时,﹣3﹣x+1﹣x=6, 解得 x=﹣4, 点 P 在点 B 的右边时,x﹣1+x﹣(﹣3)=6, 第 8页(共 8页) 解得 x=2, 综上所述,x=﹣4 或 2; (3)由两点之间线段最短可知,点 P 在 AB 之间时点 P 到点 A,点 B 的距离之和最小, 所以 x 的取值范围是﹣3≤x≤1; (4)设运动时间为 t,点 P 表示的数为﹣3t,点 E 表示的数为﹣3﹣t,点 F 表示的数为 1﹣4t, ∵点 P 到点 E,点 F 的距离相等, ∴|﹣3t﹣(﹣3﹣t)|=|﹣3t﹣(1﹣4t)|, ∴﹣2t+3=t﹣1 或﹣2t+3=1﹣t, 解得 t= 或 t=2. 故答案为:(1)﹣1;(2)﹣4 或 2;(3)﹣3≤x≤1;(4) 或 2.查看更多