- 2021-05-25 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件- 15-2-2 分式的加减 课件(共15张PPT)_人教新课标
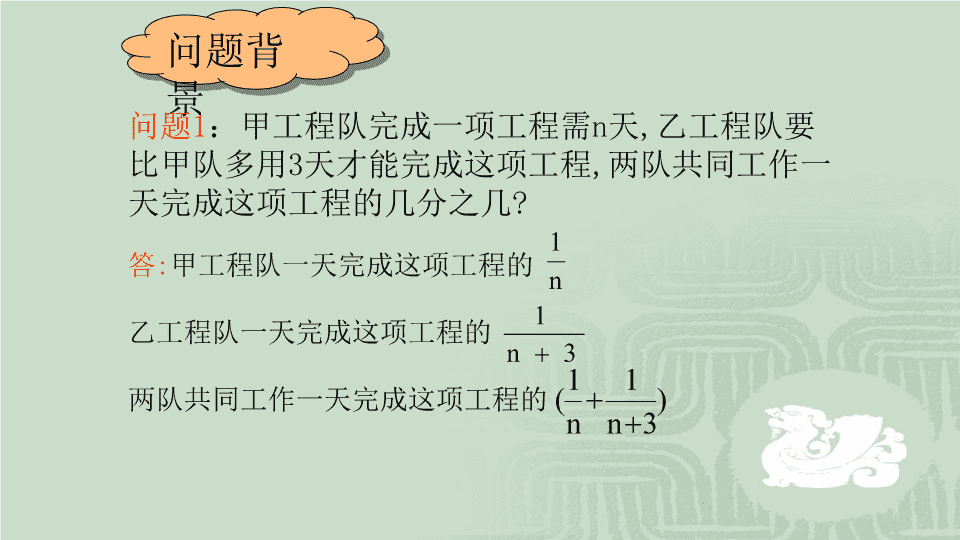
分式的加减 复习引 入 ? 5 2 5 1? 5 2 5 1: 请计算 2 1 3 1 2 1 3 1 + =-= ? ? 我们回忆一下分数的加减法是怎样进行的呢? 问题背 景 问题1:甲工程队完成一项工程需n天,乙工程队要 比甲队多用3天才能完成这项工程,两队共同工作一 天完成这项工程的几分之几? 答:甲工程队一天完成这项工程的 乙工程队一天完成这项工程的 两队共同工作一天完成这项工程的 n 1 3n 1 ) 3n 1 n 1( 问题背 景 问题2:2001年,2002年,2003年某地的森林面积(单 位:公顷)分别是S1,S2,S3,2003年与2002年相比, 森林面积增长率提高了多少? 答:2003年的森林面积增长率是 2002年的森林面积增长率是 2003年与2002年相比,森林面积增长率提高了 2 23 s ss 1 12 s ss 1 12 2 23 s ss s ss 从上面两个问题可知,在讨论实际问题的数量 关系时,需要进行分式的加减法运算。这就是 我们这节课所要学的内容——分式的加减法 想 一 想 1、你还记得分数的加减法法则吗? 2、分式的加减法的实质与分数的加减法 相同,你能说出分式的加减法法则? 3、请同学们说出 22432 9 1, 3 1, 2 1 xyyxyx 的最简公分母是什么?你能说出最简公分母的 确定方法吗? 探究新 知 同分母分式相加减,分母不变,把分子相加减。 用式子表示是: c a c b c ba ± = 异分母分式相加减,先通分,变为分母的分式,再加减。 用式子表示为: b a d c bd bcad ± = (注意:异分母的分式加减法的运算, 关键是通分,通分 的关键是正确确定几个分式的最简公分母) 分式的加减法法则: 相关知识一 通分:根据分式的基本性质,把几个异分母的分 式分别化成与原来的分式相等的同分母的分式,叫 做通分。 分式通分时,要注意几点: (1)如果各分母的系数都是整数时通分,常取它们的系数的最小 公倍数,作为最简公分母的系数; (2)若分母的系数不是整数时,先用分式的基本性质将其化为整 数,再求最小公倍数; (3)分母的系数若是负数时,应利用符号法则,把负号提取到分 式前面; (4)若分母是多项式时,先按某一字母顺序排列,然后再进行 因式分解,再确定最简公分母。 相关知识二 确定最简公分母的一般步骤: (1)找系数:如果各分母的系数都是整数,那么取它们的最 小公倍数。 (2)找字母:凡各分母因式中出现的所有字母或含字母的式 子都要选取。 (3)找指数:取分母因式中出现的所有字母或含字母的式子 中指数最大的。 ※ 这样取出的因式的积,就是最简公分母。 相关知识三 异分母的分式加减法的一般步骤: (1)通分,将异分母的分式化成同分母的分式; (2)写成“分母相同,分子相加减”的形式; (3)分子去括号,合并同类项; (4)分子、分母约分,将结果化成最简分式或整式 例题讲 解 计算: 222222 3223 yx yx yx yx yx yx (1) 222222 3223 yx yx yx yx yx yx 解: 分 子 为 多 项 式 时 , 应 把 多 项 事 看 作 一 个 整 体 加 上 括 号 参 加 运 算 , 结 果 也 要 约 分 化 成 最 简 分 式 22 )32()2()3( yx yxyxyx = 22 22 yx yx = yx 2 =))(( )(2 yxyx yx = 9 6 26 1 3 1 2 xx x x (2) 9 6 26 1 3 1 2 xx x x 解: )3)(3( 6 )3(2 1 3 1 xxx x x= )3)(3(2 12)3)(1()3(2 xx xxx= )3)(3(2 )96( 2 xx xx= )3)(3(2 )3( 2 xx x= 62 3 x x= 异 分 母 的 分 式 加 减 法 的 运 算 , 先 把 分 母 进 行 因 式 分 解 , 再 确 定 最 简 公 分 母,进 行 通 分 , 结 果 要 化 为 最 简 分 式 随堂练 习 计算 (4)1 3 1 a (3) mn nm 33 (2) ba ba 25 25 (1) ba ab ba ba ba ba 222 555 23 (1) mn m nm n mn nm 22 (2) 9 6 3 1 2 aa(3) ba ba ba ba ba ba ba ba 87546563 (4) 答 案 小结: (1)分式加减运算的方法思路: 通分 转化为 异分母 相加减 同分母 相加减 分子(整式) 相加减 分母不变 转化为 (2)分子相加减时,如果分子是一个多项 式,要将分子看成一个整体,先用括号括起来, 再运算,可减少出现符号错误。 (3)分式加减运算的结果要约分,化为最 简分式(或整式)。 本节课你的收获是什么? 222222 4323 ab ba ba ba ba ab (2) 1 22 ba ab a ba b (3) 222 3 3 3 43 3 65 cba ba cba ab bca ba (1) 22 64 3 46 1 46 1 xy x yxyx (4)查看更多