高考文科数学新课标1试题及答案word版

高考文科数学新课标1试题及答案word版

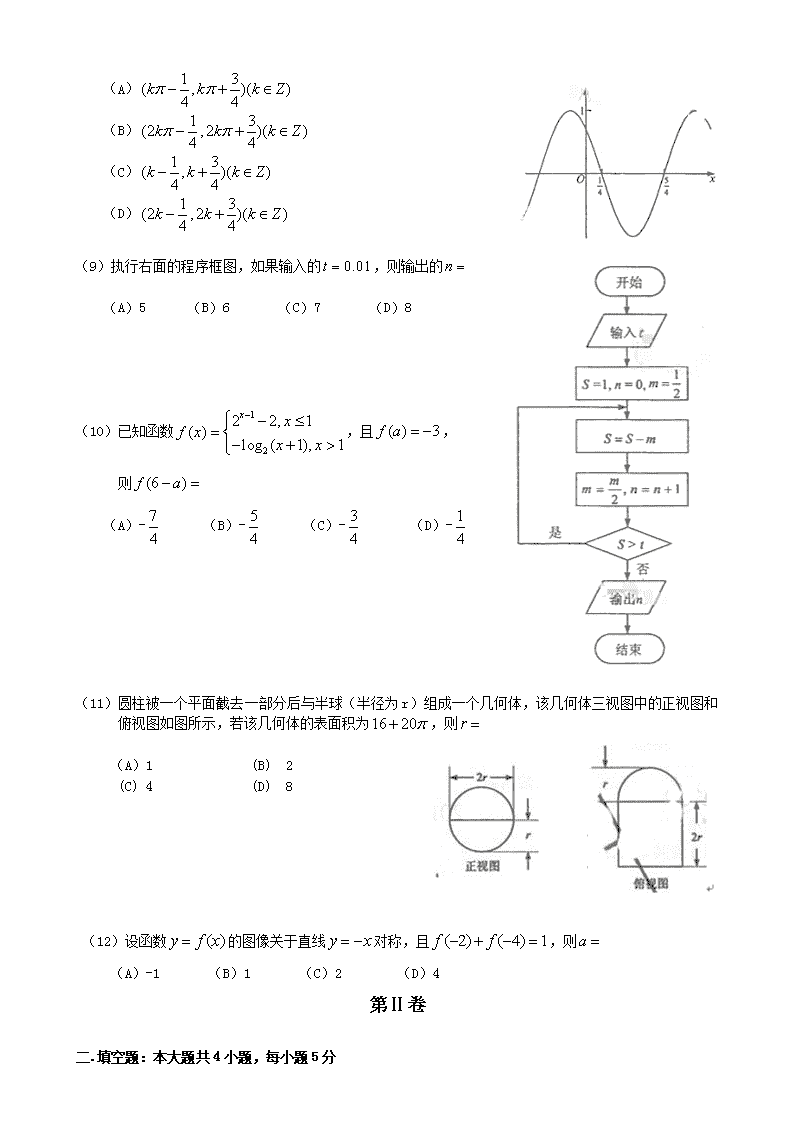
‎2015年普通高等学校招生全国统一考试文科数学 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎（1）已知集合, , 则集合中元素的个数为 ‎ （A）5 （B）4 （C）3 （D）2‎ ‎（2）已知点A（0,1），B（3,2），向量=（-4，-3），则向量=‎ ‎（A）（-7，-4） （B）（7,4） （C）（-1,4） （D）（1，4）‎ ‎（3）已知复数满足，则=‎ ‎（A） （B） （C） （D）‎ ‎（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为 ‎ （A） （B） （C） （D）‎ ‎（5）已知椭圆E的中心在坐标原点，离心率为，E的右焦点与抛物线C：的焦点重合，A，B是C的准线与E的两个焦点，则|AB|=‎ ‎ （A）3 （B）6 （C）9 （D）12 ‎ ‎（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有 A.14斛 B.22斛 C.36斛 D.66斛 ‎（7）已知是公差为1的等差数列， =4，则=‎ ‎（A） （B） （C）10 （D）12‎ ‎（8）函数的部分图像如图所示，则的单调递减区间为 ‎（A） ‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎（9）执行右面的程序框图，如果输入的，则输出的 ‎（A）5 （B）6 （C）7 （D）8‎ ‎（10）已知函数，且，‎ 则 ‎（A）- （B）- （C）- （D）-‎ ‎（11）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为，则 ‎（A）1 (B) 2‎ ‎(C) 4 (D) 8‎ ‎（12）设函数的图像关于直线对称，且，则 ‎（A）-1 （B）1 （C）2 （D）4‎ 第Ⅱ卷 二.填空题：本大题共4小题，每小题5分 ‎（13）在数列中， , , 为的前n项和。若，则________.‎ ‎（14）已知函数的图像在点处的切线过点，则 .‎ ‎（15）满足约束条件，则的最大值为________.‎ ‎（16）已知F是双曲线C：的右焦点，P是C的左支上一点，A（0,6）.当△APF周长最小时，该三角形的面积为_____________.‎ 三.解答题：解答应写出文字说明，证明过程或演算步骤 ‎（17）（本小题满分12分）‎ 已知a，b，c分别为△ABC内角A，B，C的对边，.‎ ‎（Ⅰ）若，求；‎ ‎（Ⅱ）设，且，求△ABC的面积。‎ ‎（18）（本小题满分12分）‎ 如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.‎ ‎（Ⅰ）证明：平面AEC⊥平面BED；‎ ‎（Ⅱ）若∠ABC=120°，AE⊥EC，三棱锥E—ACD的体积为，求该三棱锥的侧面积。‎ ‎（19）（本小题满分12分）‎ 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费和年销售量（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。‎ ‎（x1-）2‎ ‎（w1-）2‎ ‎（x1-）(y-)‎ ‎（w1-）(y-)‎ ‎46.6‎ ‎563‎ ‎6.8‎ ‎289.8‎ ‎1.6‎ ‎1469‎ ‎108.8‎ 表中w1 =1, ， =1‎ ‎（I）根据散点图判断，与哪一个适宜作为年销售量关于年宣传费的回归方程类型？（给出判断即可，不必说明理由）‎ ‎（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程；‎ ‎（Ⅲ）已知这种产品的年利率z与x、y的关系为。根据（Ⅱ）的结果回答下列问题：‎ ‎（1）年宣传费时，年销售量及年利润的预报值是多少？‎ ‎（2）年宣传费为何值时，年利润的预报值最大？‎ 附：对于一组数据（u1 v1）,（u2 v2）…….. （un vn）,其回归线v=u的斜率和截距的最小二乘估计分别为：‎ ‎（20）（本小题满分12分）‎ 已知过点A(0,1)且斜率为k的直线l与圆C: 交于M,N两点.‎ （1） 求k的取值范围；‎ （2） 若· =12，其中0为坐标原点，求︱MN︱.‎ ‎（21）（本小题满分12分）‎ ‎ 设函数。‎ ‎ （Ⅰ）讨论的导函数零点的个数；‎ ‎ （Ⅱ）证明：当时，。‎ ‎ ‎ 请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分。作答时请写清题号。‎ ‎（22）（本小题满分10分）选修4-1：几何证明选讲 ‎ 如图，AB是⊙的直径，AC是⊙的切线，BC交⊙于点E。‎ ‎（Ⅰ）若D为AC的中点，证明：DE是⊙的切线； ‎ ‎（Ⅱ）若CA=CE，求∠ACB的大小。‎ ‎（23）（本小题满分10分）选修4-4；坐标系与参数方程 ‎ 在直角坐标系中，直线:x=,圆：，以坐标原点为极点，轴的正半轴为极轴建立极坐标系。‎ ‎（1）求的极坐标方程。‎ ‎（2）若直线的极坐标为=（ρR）,设与的交点为M，N,求△C2MN的面积.‎ ‎（24）（本小题满分10分）选修4-5：不等式选讲 已知函数，.‎ （1） 当时，求不等式的解集；‎ （2） 若的图像与轴围成的三角形面积大于6，求的取值范围.‎ 答案及评分标准 一、选择题：DACCBB BDCABC 二、填空题： 13.6 14.1 15.4 16. ‎ 三、解答题 ‎（17）解：‎ ‎（1）由得 又 故 ‎ ‎（2）由得，故，又 故 ‎ ‎（18）解：‎ ‎（1） 四边形ABCD为菱形， 又BE⊥平面ABCD， 平面 ‎ ‎ ‎ 又平面, 平面AEC⊥平面BED ‎(2) 设，则, , ,‎ ‎ , 故，解得 ‎ 所求侧面积为 ‎（19）解：‎ ‎（1）选 ‎（2），，回归方程为 ‎（3）1. 时，，‎ ‎2. ，‎ 当，即时，取得最大值。‎ 故宣传费为千元时，年利润的预报值最大。‎