20130413温州市中考数学模拟试题

20130413温州市中考数学模拟试题

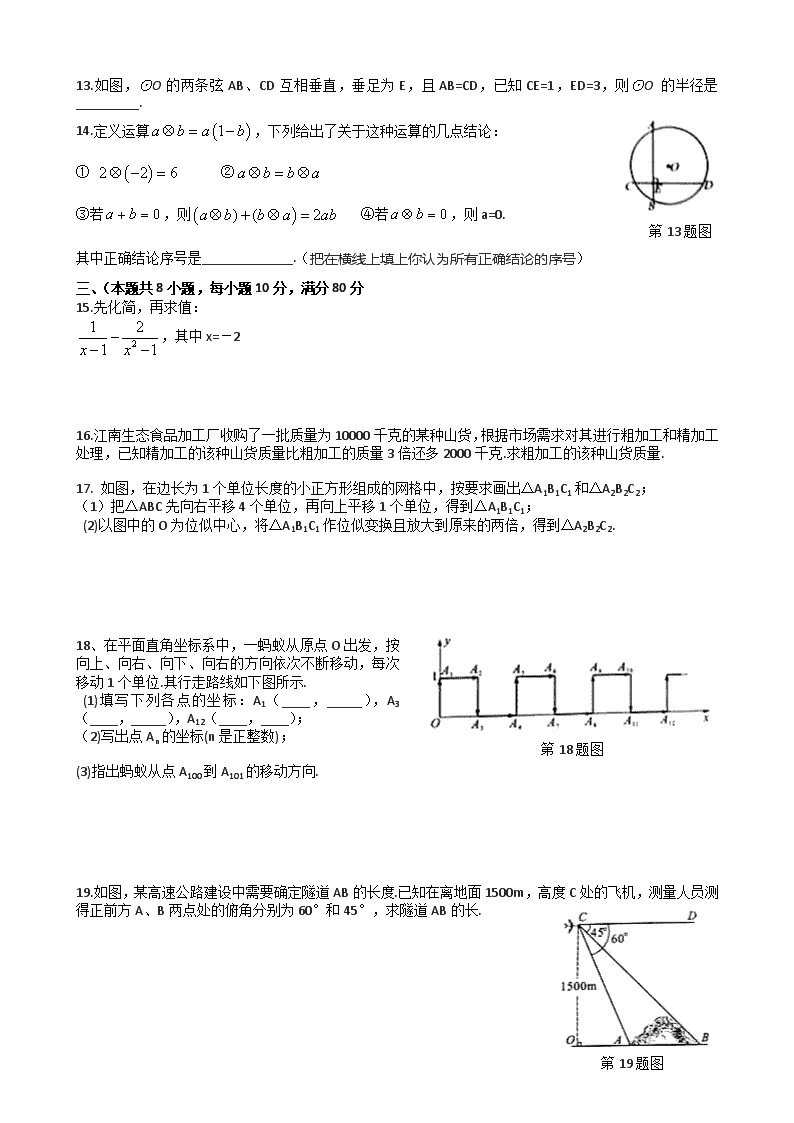
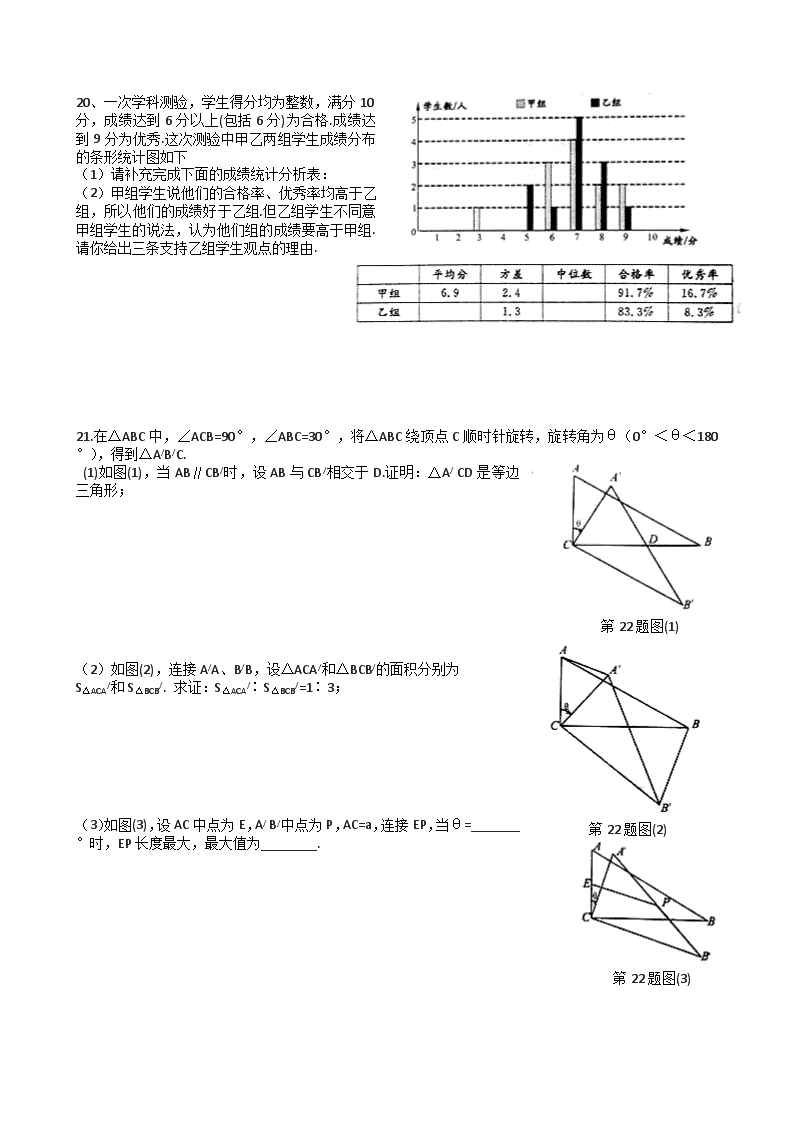
‎2013年温州市中考数学模拟试题 ‎ 一、选择题（本题共10小题，每小题4分，满分40分）‎ ‎1.－2，0，2，－3这四个数中最大的是……………【 】‎ A.－1 B‎.0 ‎ C.1 D.2‎ ‎2.2010年末森林面积为3804.2千公顷，用科学记数法表示3804.2千正确的是…………………………………………………………………【 】‎ A.3804.2×103 B.380.42×‎104 ‎ C.3.842×106 D.3.842×105‎ ‎3. 下图是五个相同的小正方体搭成的几体体，其左视图是…………………………………【 】‎ 第3题图 ‎4.设，a在两个相邻整数之间，则这两个整数是…………【 】‎ A.1和2 B.2和‎3 ‎ C.3和4 D.4 和5 ‎ 第6题图 ‎5.从下五边形的五个顶点中，任取四个顶点连成四边形，对于事件M，“这个四边形是等腰梯形”.下列推断正确的是………………………………………………【 】‎ A.事件M是不可能事件 B. 事件M是必然事件 C.事件M发生的概率为D. 事件M发生的概率为 ‎6如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是……………【 】 ‎ ‎ A.7 B.9‎ 第7题图 C.10 D. 11 ‎ ‎7. 如图，⊙半径是1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧的长是………………………………………【 】‎ A. B. C. D. ‎ ‎8.一元二次方程的根是……【 】‎ A.－1 B. ‎2 ‎ C. 1和2 D. －1和2‎ 第9题图 ‎9.如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=，CD=，点P在四边形ABCD上，若P到BD的距离为，则点P的个数为……………………………【 】 ‎ A.1 B‎.2 C.3 D.4 ‎ ‎10.如图所示，P是菱形ABCD的对角线AC上一动点，过P垂直于AC的直线交菱形ABCD的边于M、N两点，设AC=2，BD=1，AP=x，则△AMN的面积为y，则y关于x的函数图象的大致形状是…………………………………………………【 】‎ 第10题图 二、填空题（本题共4小题，每小题5分，满分20分）‎ ‎ 11.因式分解：=_________.‎ ‎12.根据里氏震级的定义，地震所释放的相对能量E与地震级数n的关系为：，那么9级地震所释放的相对能量是7级地震所释放的相对能量的倍数是 ．‎ ‎13.如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O 的半径是_________.‎ 第13题图 ‎14.定义运算，下列给出了关于这种运算的几点结论：‎ ‎① ② ‎ ‎③若，则 ④若，则a=0.‎ 其中正确结论序号是_____________.（把在横线上填上你认为所有正确结论的序号）‎ 三、（本题共8小题，每小题10分，满分80分 ‎15.先化简，再求值：‎ ‎，其中x=－2‎ ‎16.江南生态食品加工厂收购了一批质量为10000千克的某种山货，根据市场需求对其进行粗加工和精加工处理，已知精加工的该种山货质量比粗加工的质量3倍还多2000千克.求粗加工的该种山货质量.‎ ‎17. 如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B‎1C1和△A2B‎2C2；‎ ‎（1）把△ABC先向右平移4个单位，再向上平移1个单位，得到△A1B‎1C1；‎ ‎(2)以图中的O为位似中心，将△A1B‎1C1作位似变换且放大到原来的两倍，得到△A2B‎2C2.‎ 第18题图 ‎18、在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位.其行走路线如下图所示.‎ ‎(1)填写下列各点的坐标：A1（____，_____），A3（____，_____），A12（____，____）；‎ ‎（2)写出点An的坐标(n是正整数)；‎ ‎(3)指出蚂蚁从点A100到A101的移动方向.‎ 第19题图 ‎19.如图，某高速公路建设中需要确定隧道AB的长度.已知在离地面‎1500m，高度C处的飞机，测量人员测得正前方A、B两点处的俯角分别为60°和45°，求隧道AB的长.‎ ‎20、一次学科测验，学生得分均为整数，满分10分，成绩达到6分以上(包括6分)为合格.成绩达到9分为优秀.这次测验中甲乙两组学生成绩分布的条形统计图如下 ‎（1）请补充完成下面的成绩统计分析表：‎ ‎（2）甲组学生说他们的合格率、优秀率均高于乙组，所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法，认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.‎ 第22题图(1)‎ ‎21.在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A/B/C.‎ ‎(1)如图(1)，当AB∥CB/时，设AB与CB/相交于D.证明：△A/ CD是等边三角形；‎ 第22题图(2)‎ ‎（2）如图(2)，连接A/A、B/B，设△ACA/和△BCB/的面积分别为 S△ACA/和S△BCB/. 求证：S△ACA/∶S△BCB/=1∶3；‎ 第22题图(3)‎ ‎（3）如图(3)，设AC中点为E，A/ B/中点为P，AC=a，连接EP，当θ=_______°时，EP长度最大，最大值为________.‎ 第23题图 ‎22.如图，正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直线中相邻两条之间的距离依次为h1、h2、h3（h1＞0，h2＞0，h3＞0）. ‎ ‎(1)求证h1=h3； ‎ ‎(2) 设正方形ABCD的面积为S.求证S=（h2+h3）2＋h12；‎ ‎(3)若,当h1变化时，说明正方形ABCD的面积为S随h1的变化情况.‎ 数学答案 ‎1～5ACACB 6～10DBDBC ‎11. ； 12. 100； 13. 14. ①③.‎ ‎15. 原式=.‎ ‎16. 设粗加工的该种山货质量为x千克，根据题意，得 x+(3x+2000)=10000.‎ ‎ 解得 x=2000.‎ ‎ 答：粗加工的该种山货质量为2000千克.‎ ‎17. 如下图 A A1‎ B C B1‎ C1‎ A2‎ B2‎ C2‎ ‎·‎ O ‎18．⑴A1(0,1) A3(1,0) A12(6,0) ‎ ‎⑵An(2n,0)‎ ‎⑶向上 ‎19. 简答：∵OA， OB=OC=1500，‎ ‎ ∴AB=(m).‎ ‎ 答：隧道AB的长约为‎635m.‎ ‎20. （1）甲组：中位数 7； 乙组：平均数7， 中位数7‎ ‎（2）（答案不唯一）‎ ‎①因为乙组学生的平均成绩高于甲组学生的平均成绩，所以乙组学生的成绩好于甲组；‎ ‎②因为甲乙两组学生成绩的平均分相差不大，而乙组学生的方差低于甲组学生的方差，说明乙组学生成绩的波动性比甲组小，所以乙组学生的成绩好于甲组；‎ ‎③因为乙组学生成绩的最低分高于甲组学生的最低分，所以乙组学生的成绩好于甲组.‎ ‎21.（1）易求得, , 因此得证.‎ ‎(2)易证得∽,且相似比为，得证.‎ ‎（3）120°， ‎ ‎22.（1）过A点作AF⊥l3分别交l2、l3于点E、F，过C点作CH⊥l2分别交l2、l3于点H、G，‎ 证△ABE≌△CDG即可.‎ ‎（2）易证△ABE≌△BCH≌△CDG≌△DAF,且两直角边长分别为h1、h1+h2,四边形EFGH是边长为h2的正方形，‎ 所以.‎ ‎(3)由题意，得 所以 又 解得0＜h1＜‎ ‎∴当0＜h1＜时，S随h1的增大而减小；‎ ‎ 当h1=时，S取得最小值；当＜h1＜时，S随h1的增大而增大.‎