- 2021-05-24 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件《反比例函数》 (11)_苏科版
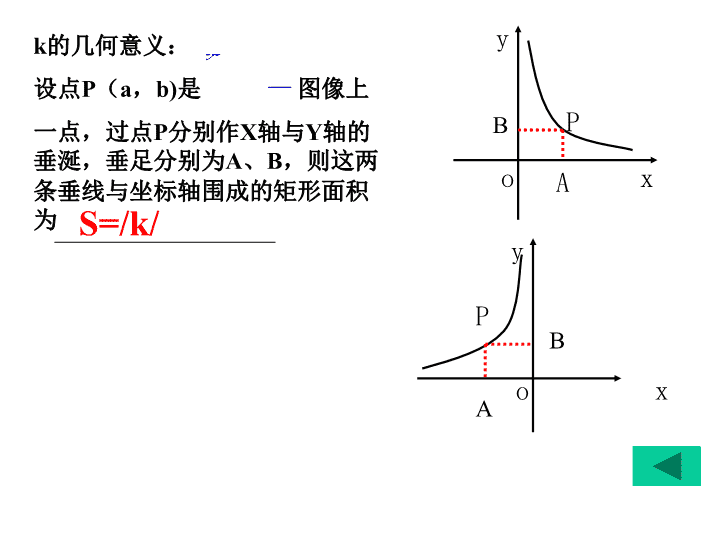
一、考点:反从例函数的意义及其图象和性质 2.反比例函数的概念需注意以下几点: (1)k为常数,k≠0; K的几何意义。 (2)自变量x的取值范围是x≠0的一切实数,且要使实际 问题有意义。 x ky y=kx-1 xy=k 1.反比例函数:一般地,形如 (k为常数, k≠0)的函数叫做反比例函数.其中x是自变量, y是x的函数,k是比例系数. ky x P Ao y x y B P o xA B k的几何意义: 设点P(a,b)是 图像上 一点,过点P分别作X轴与Y轴的 垂涎,垂足分别为A、B,则这两 条垂线与坐标轴围成的矩形面积 为 ky x S=/k/ 反比例函数 (k为常数,k≠0)的图象是双曲线,具有如 下的性质: ①当k>0时,双曲线的两支分别在第一、三象限,在每个象限内, y随x的增加而减小; ②当k<0时,双曲线的两支分别在第二、四象限,在每个象限内, y随x的增大而增大. ky x 注意:双曲线的两分支都无限的接近坐 标轴,但是永远不能到达x轴、 y轴。 3.反比例函数的图象和性质. 4.反比例函数的图像的对称性 (1)轴对称图形 ,对称轴是 (2)中心对称图形,即双曲线的两支曲线关于 成中心对称。 双曲线一支上任意一点A(a,b)关于原点的 对称点A’(-a,-b)必在双曲线的另一支上。 (1)下列的数表中分别给出了变量y与x之间的对 应函数关系,其中有一个表示的是反比例函数, 你能把它找出来吗? x 1 2 3 4 y 6 8 9 7 x 1 2 3 4 y 8 5 4 3 x 1 2 3 4 y 5 8 7 6 x 1 2 3 4 y 2 1 2/3 1/2 A B C D 基础训练 D (2)已知y= 22 1( 1) mm x 如果y是x的正比例函数,m= . 如果y是x的反比例函数,m= . -1 0 (3)在函数y= (k<0)的图像上有A(1,a), B(-1,b),C(-2,c)三点,下列各式正确的是( ) A、a查看更多