- 2021-05-24 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】新疆喀什巴楚县第一中学2019-2020学年高一下学期期末考试试题(解析版)
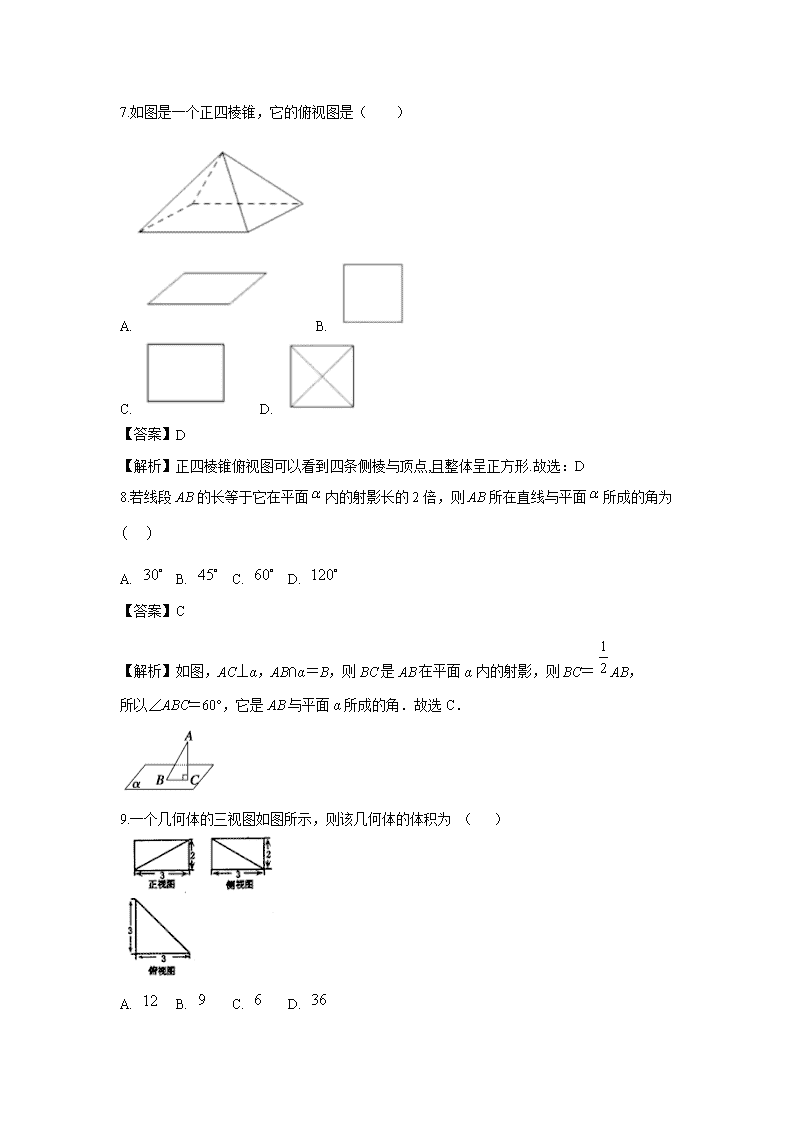
新疆喀什巴楚县第一中学2019-2020学年 高一下学期期末考试试题 一、单选题 1.已知直线斜率的绝对值等于1,则此直线的倾斜角( ) A. B. C. D. 或135° 【答案】D 【解析】, 当斜率为1时,直线的倾斜角为;当斜率为时,直线的倾斜角为135°. 故选:D 2.下列命题正确的是( ) A. 经过三点确定一个平面 B. 经过一条直线和一个点确定一个平面 C. 两两相交且不共点的三条直线确定一个平面 D. 四边形确定一个平面 【答案】C 【解析】A选项,根据平面基本性质知,不共线的三点确定一个平面,故错误;B选项,根据平面基本性质公理一的推论,直线和直线外一点确定一个平面,故错误;C选项,根据公理一可知,不共线的三点确定一个平面,而两两相交且不共点的三条直线,在三个不共线的交点确定的唯一平面内,所以两两相交且不共点的三条直线确定一个平面,正确;选项D,空间四边形不能确定一个平面,故错误;综上知选C. 3.下列几何体中,不是旋转体的是( ) A. B. C. D. 【答案】A 【解析】由题,B圆柱,C圆锥,D球均为旋转体. 故选:A 4.已知直线,平面,且,下列条件中能推出的是( ) A. B. C. D. 与相交 【答案】C 【解析】A中,若,由,可得;故A不满足题意; B中,若,由,可得;故B不满足题意; C中,若,由,可得;故C正确; D中,若与相交,由,可得异面或平,故D不满足题意.故选C 5.下图中的直线、、的斜率分别为、、,则( ) A. B. C. D. 【答案】D 【解析】由图可知:,,,且直线的倾斜角小于直线的倾斜角, 所以,综上可知:. 故选:D. 6.两条直线:x=2和:交点坐标是( ) A. B. C. D. 【答案】A 【解析】, 所以两条直线的交点坐标为.故选:A 7.如图是一个正四棱锥,它的俯视图是( ) A. B. C. D. 【答案】D 【解析】正四棱锥俯视图可以看到四条侧棱与顶点,且整体呈正方形.故选:D 8.若线段AB的长等于它在平面内的射影长的2倍,则AB所在直线与平面所成的角为 A. B. C. D. 【答案】C 【解析】如图,AC⊥α,AB∩α=B,则BC是AB在平面α内的射影,则BC=AB, 所以∠ABC=60°,它是AB与平面α所成的角.故选C. 9.一个几何体的三视图如图所示,则该几何体的体积为 ( ) A. B. C. D. 【答案】C 【解析】由三视图可知,此几何体为四棱锥A-BCFE, . 故选C. 10.经过点,斜率是-2的直线方程( ) A. x-2y+10=0 B. 2x+y-14=0 C. x+y-14=0 D. 2x+2y-10=0 【答案】B 【解析】经过点,斜率是-2的直线方程为即. 故选:B 11.若直线a不平行于平面,则下列结论成立的是( ) A. 内的所有直线都与直线a异面 B. 内不存在与a平行的直线 C. 内的直线都与a相交 D. 直线a与平面有公共点 【答案】D 【解析】直线不平行于,包括两种情况:或,当时,内的所有直线都与直线共面,A错;当时,内必然有直线与直线平行, B错;从而C也错;当,直线和平面有无数个公共点,当,直线与平面有唯一公共点,D正确. 12.已知点,的距离是17 ,则a的值是( ) A. 8 B. 6 C. ±8 D. ±6 【答案】C 【解析】,即,. 故选:C 二、填空题 13.已知点,,则直线的方程是________. 【答案】 【解析】直线的两点式方程为 代入,,得 整理得直线的方程是. 故答案为: . 14.一个球的表面积是,那么这个球的体积等于_______ 【答案】 【解析】设球的半径为,则,得, 球的体积.故答案为:. 15.点P(-1,2)到直线l:3x=2的距离是________. 【答案】 【解析】直线l:即,点P(-1,2)到直线l的距离为. 故答案为: 16.已知两个平面垂直,下列命题中正确的命题是______. ①一个平面内已知直线必垂直于另一个平面内的任意一条直线 ②一个平面内的已知直线必垂直于另一个平面的无数条直线 ③一个平面内的任一条直线必垂直于另一个平面 ④过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面 【答案】② 【解析】①错误,当一个平面内的一条直线平行于两个平面的交线时不满足条件; ②正确,两个平面垂直则一个平面内的一条直线必垂直于另外一个平面内的无数条直线; ③错误,在其中一个平面内可以找到一条直线平行于另一个平面,如与交线平行的直线即可; ④错误,如果该点在交线上,过交点上一点作垂线不一定垂直另一个平面. 故答案为:② 三、解答题 17.已知正四棱台上、下底面的边长分别为4、10,侧棱长为6.求正四棱台的表面积. 【解】如图,正四棱台中,, 在等腰梯形 中,过作于,则, 所以, 所以正四棱台的表面积为 18.直线经过点A(3,2),且与直线:4x+y-2=0 平行 (1)求直线的方程; (2)求此两条直线间的距离; 【解】(1)根据题意设直线的方程为:, 因为直线过点,所以, 所以直线的方程为:; (2)两直线间的距离为. 19.如图所示,空间四边形ABCD中,E,F,G 分别是AB,BC,CD 的中点, (1)证明:直线BD平行于平面EFG; (2)证明:直线AC平行于平面EFG. 【解】(1)F,G 分别是BC,CD 的中点, FG为的中位线,则, 又平面EFG,平面EFG,平面EFG. (2)E,F分别是AB,BC的中点, EF为的中位线,则, 又平面EFG,平面EFG,平面EFG. 20.(1)求在x轴上与点A(5,12)的距离为13的点的坐标. (2)已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标. 【解】(1)设x轴上点的坐标为, 由距离公式可得,解得或, 所以所求点的坐标为或; (2)设点P的纵坐标为y, 由距离公式可得,解得或, 所以点P的纵坐标为或11. 21.如图所示,在正方体ABCD﹣A1B1C1D1中,棱长AB=1. (Ⅰ)求异面直线A1B与 B1C所成角大小;(Ⅱ)求证:平面A1BD∥平面B1CD1. 【解】(Ⅰ)因B1C//A1D,所以为异面直线A1B与B1C所成角. 在中,易得 (Ⅱ), ,,且 所以 22.已知直线经过两条直线:和:的交点,直线:; (1)若,求的直线方程; (2)若,求的直线方程. 【解】(1)由,得, ∴与的交点为. 设与直线平行的直线为, 则,∴. ∴所求直线方程为. (2)设与直线垂直的直线为, 则,解得. ∴所求直线方程为.查看更多