- 2021-05-24 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁高考文科数学
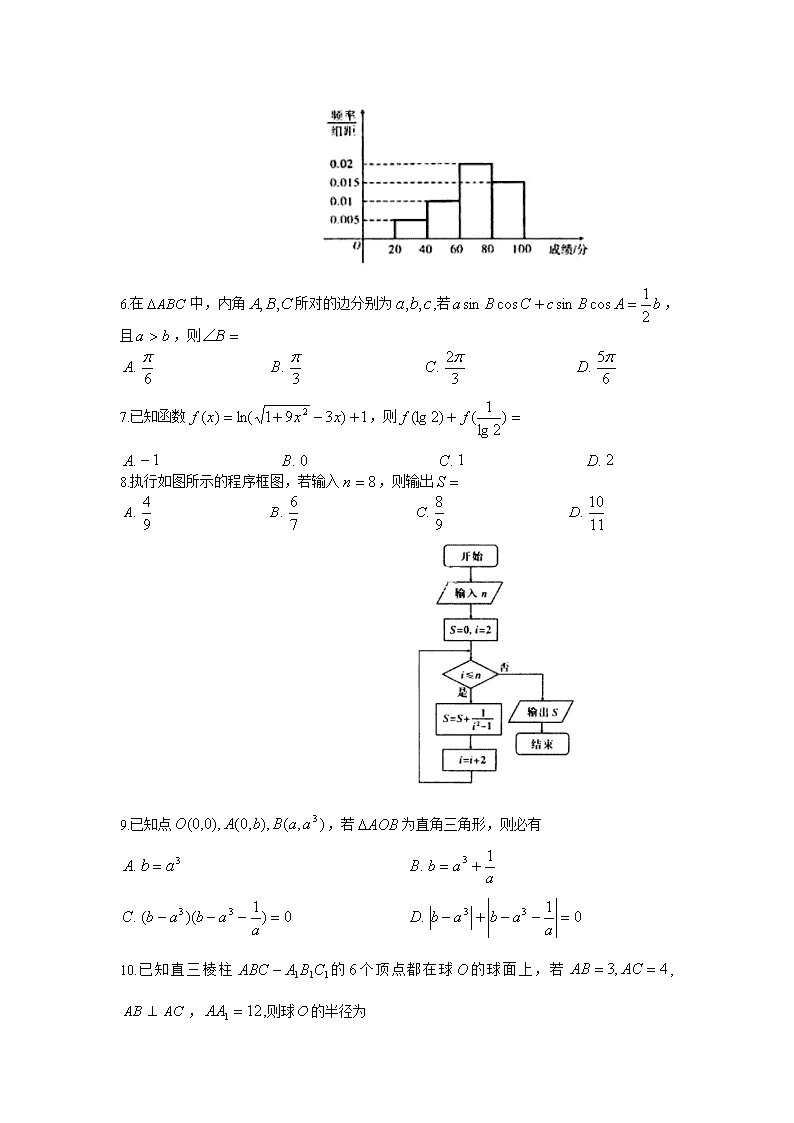
2013年普通高等学校招生全国统一考试(辽宁卷) 数学(文科) 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合,,则 2. 复数的模长为 3.已知点,,则与向量同方向的单位向量为 4.下列关于公差的等差数列的四个命题: 数列是递增数列 数列是递增数列 数列是递增数列 数列是递增数列 其中真命题是 5.某班全体学生参加英语测试,成绩分布的频率分布直方图如图,数据的分组依次为:,,,。若低于60分的人数是15,则该班级学生人数是 6.在中,内角所对的边分别为,若,且,则 7.已知函数,则 8.执行如图所示的程序框图,若输入,则输出 9.已知点,若为直角三角形,则必有 10.已知直三棱柱的个顶点都在球的球面上,若,,,则球的半径为 11. 已知椭圆的左焦点,与过原点的直线相交于两点,连结,若,,则的离心率为 12. 已知函数满足,。设,(表示中的较大值,表示中的较小值),记的最小值为,的最大值为,则 第Ⅱ卷 二、填空题 13.某几何体的三视图如图所示,则该几何体的体积是 。 14.已知等比数列是递增数列,是的前项和,若是方程的两个根,则= 。 15.已知为双曲线的左焦点,为上的点,若的长等于虚轴长的2倍,点在线段上,则的周长为 16.为了考察某校各班参加课外小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据,已知样本平均数为7,样本方差为4,且样本数据互不相同,则样本数据中的最大值为 。 三、解答题 17.设向量,,。 (1)若,求的值; (2)设函数,求的最大值。 18.如图,是圆的直径,圆所在的平面,是圆上的点。 (1)求证:平面; (2)若为的中点,为的重心,求证:∥平面 P A B O C G Q 19.现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答。 (1)所取的2道题都是甲类题的概率; (2)所取的2道题不是同一类题的概率。 20.如图,抛物线,点在抛物线上,过作的切线,切点为(为原点时,重合于)。当时,切线的歇斜率为。 (1)求的值; (2)当在上运动时,求线段中点的轨迹方程(重合于时,中点为)。 21.(1)证明:当时,; (2)若不等式对恒成立,求实数的取值范围。 22.(选修几何证明选讲)如图,为⊙的直径,直线与⊙相切于,垂直于,垂直于,垂直于于,连接,证明: (1); (2) A B C D E F O 23.(选修4-4极坐标与参数方程) 在直角坐标系中,以为极点,轴正半轴为极轴建立直角坐标系,圆,直线的极坐标方程分别为,。 (1) 求与交点的极坐标; (2) 设为的圆心,为与交点连线的中点,已知直线的参数方程为(为参数),求的值。 24. (选修4-5不等式选讲) 已知函数,其中 (1) 当时,求不等式的解集; (2) 已知关于的不等式的解集,求的值。 2013年普通高等学校招生全国统一考试(辽宁卷) 参考答案 一.选择题 1.【答案】B 【解析】 由已知,所以,选B。 2.【答案】B 【解析】由已知所以 3.【答案】A 【解析】,所以,这样同方向的单位向量是 4.【答案】D 【解析】设,所以正确;如果则满足已知,但并非递增所以错;如果若,则满足已知,但,是递减数列,所以错;,所以是递增数列,正确 5.【答案】B 【解析】第一、第二小组的频率分别是、,所以低于60分的频率是0.3,设班级人数为,则,。 6.【答案】A 【解析】边换角后约去,得,所以,但B非最大角,所以。 7.【答案】D 【解析】所以,因为,为相反数,所以所求值为2. 8.【答案】A 【解析】的意义在于是对求和。因为,同时注意,所以所求和为= 9.【答案】C 【解析】若A为直角,则根据A、B纵坐标相等,所以;若B为直角,则利用得,所以选C 10.【答案】C 【解析】由球心作面ABC的垂线,则垂足为BC中点M。计算AM=,由垂径定理,OM=6,所以半径R= 11.【答案】B 【解析】由余弦定理,AF=6,所以,又,所以 12.【答案】C 【解析】顶点坐标为,顶点坐标,并且与的顶点都在对方的图象上,图象如图, A、B分别为两个二次函数顶点的纵坐标,所以A-B= 【方法技巧】(1)本题能找到顶点的特征就为解题找到了突破口。(2)并不是A,B在同一个自变量取得。 二.填空题 13. 【答案】 【解析】直观图是圆柱中去除正四棱柱。 14. 【答案】63 【解析】由递增,,所以,代入等比求和公式得 15. 【答案】44 【解析】两式相加,所以并利用双曲线的定义得,所以周长为 16. 【答案】10 【解析】设五个班级的数据分别为。由平均数方差的公式得,,显然各个括号为整数。设分别为,,则。设= =,由已知,由判别式得,所以,所以。 三.解答题 (17)【解析】 (I) . (II) (18)【解析】由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC,又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC. (II) 连OG并延长交AC与M,链接QM,QO. 由G为∆AOC的重心,得M为AC中点,由G为PA中点,得QM//PC. 又O为AB中点,得OM//BC.因为QM∩MO=M,QM⊂平面QMO.所以QG//平面PBC. (19)【解析】 (I)将4道甲类题依次编号为1,2,3,4;2道一类题依次编号为5.6,任取2道题,基本事件为:{1,2},{1,3},{1,4},{1,5},{1,6},{2,3},{2,4},{2,5},{2,6},{3,4},{3,5},{3,6},{4,5},{4,6},{5,6},共15个,而且这些基本事件的出现是等可能的. 用A表示“都是甲类题”这一事件,则A包含的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,所以 P(A)= (II)基本事件向(I),用B表示“不是同一类题”这一事件,则B包含的基本事件有{1,5},{1,6},{2,5},{2,6},{3,5},{3,6},{4,5},{4,6},共8个,所以P(B)=. (20)【解析】 (I)因为抛物线上任意一点(x,y)的切线斜率为,且切线MA的斜率为,所以A点坐标为,故切线MA的方程为 . 因为点在切线MA 抛物线C上,于是 ① ② 由①②得p=2. 设N(x,y),A ③ ④ 切线MA、MB的方程为 ⑤ ⑥ 由⑤⑥得MA、MB的交点M()的坐标为 ⑦ 由③④⑦得 当时,A、B重和于远点0,AB重点N为0,坐标满足因此AB中点N的轨迹方程为 (21)【解析】记F(x)= (II)因为当时. (22)【解析】证明: (I)由直线CD与⊙O相切,得∠CEB∠EAB,由AB为⨀O的直径,得AE⊥AB,得∠EAB+∠EBF=; 又EF⊥AB,故∠FEB=∠CEB. (II) (23)【解析】 (I) 圆C的直角坐标方程为 直线C的直角坐标方程为x+y-4=0. 解 所以交点的极坐标为, 注:极坐标系下点的表示不唯一. (II)由(I)可得,P点与Q点的直角坐标分别为(0,2),(1,3). 故直线PQ的直角坐标方程为x-y+2=0. 由参数方程可得y=. 所以 解得, (24)【解析】 (I)当a=2时, 当 (II)记 于是a=3查看更多