- 2021-05-24 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版九年级上册数学同步课件-第22章-22二次函数与一元二次方程
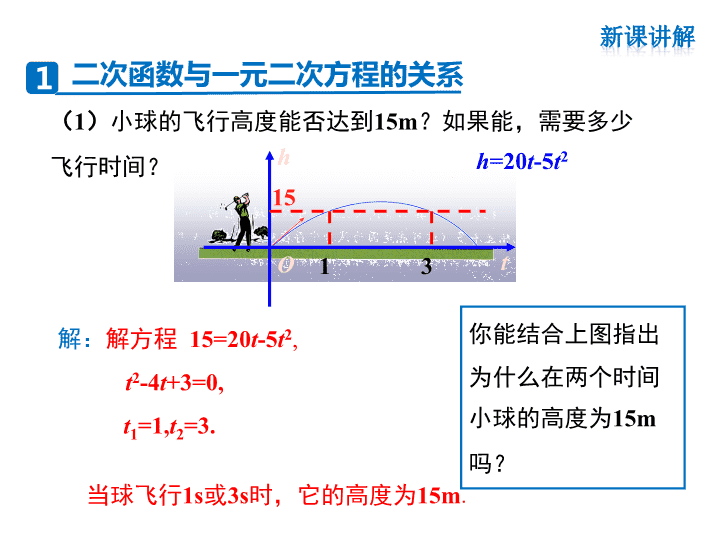
22.2 二次函数与一元二次方程 第二十二章 二次函数 问题: 如图,以40m/s的速度将小球沿与地面成30°角的方 向击出时,小球的飞行路线将是一条抛物线.如果不考虑空 气的阻力,小球的飞行高度h(单位:m)与飞行时间t(单 位:s)之间具有关系h=20t-5t2,考虑以下问题: (1)小球的飞行高度能否达到15m?如果能,需要多少 飞行时间? O h t 15 1 3 当球飞行1s或3s时,它的高度为15m. 解:解方程 15=20t-5t2, t2-4t+3=0, t1=1,t2=3. h=20t-5t2 你能结合上图指出 为什么在两个时间 小球的高度为15m 吗? 二次函数与一元二次方程的关系1 (2)小球的飞行高度能否达到20m?如果能,需要多 少飞行时间? O h t 20 4 解方程: 20=20t-5t2, t2-4t+4=0, t1=t2=2. 当球飞行2s时,它的飞行高度为20m. h=20t-5t2 你能结合上图指出 为什么只在一个时 间小球的高度为 20m? (3)小球的飞行高度能否达到20.5m?如果能,需要多 少飞行时间? O h t 你能结合上图指出 为什么小球不能达 到20.5m的高度? 20.5 解方程: 20.5=20t-5t2, t2-4t+4.1=0. 因为(-4)2-4 ×4.1<0,所以方程 无实数根.这就是说,小球的飞 行高度达不到20.5m. h=20t-5t2 (4)小球从飞出到落地要用多少时间? O h t 解方程: 0=20t-5t2, t2-4t=0, t1=0,t2=4. 当小球飞行0s和4s时,它的高度为0m. 即0s时小球从地面飞出,4s时球落回地面. h=20t-5t2 从上面发现,二次函数y=ax2+bx+c何时为一元二次方程? 一般地,当y取定值且a≠0时,二次函数为一元二次方 程. 如:y=5时,则5=ax2+bx+c就是 一个一元二次方程. 为一个常数 (定值) 所以二次函数与一元二次方程联系密切. 例如,已知二次函数y = -x2+4x的值为3,求自变量x 的值,可以看作解一元二次方程-x2+4x=3(即x2- 4x+3=0). 反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值. 利用二次函数深入讨论一元二次方程 思考 下列二次函数的图象与x轴有公共点吗?如果有,公共点的 横坐标是多少?当x取公共点的横坐标时,函数值是多少?由 此,你能得出相应的一元二次方程的根吗? (1)y=x2+x-2; (2)y=x2-6x+9; (3)y=x2-x+1. 2 1 y = x2-6x+9y = x2-x+1 y = x2+x-2 观察图象,完成下表 抛物线与x轴 公共点个数 公共点 横坐标 相 应 的 一 元 二 次 方 程 的 根 y = x2-x+1 y = x2-6x+9 y = x2+x-2 0个 1个 2个 x2-x+1=0无解 0 x2-6x+9=0,x1=x2=3 -2, 1 x2+x-2=0,x1=-2,x2=1 二次函数 y=ax2+bx+c的图象 与x轴交点 一元二次方程 ax2+bx+c=0的根 b2-4ac 有两个交点 有两个不相等的实 数根 b2-4ac > 0 有一个交点 有两个相等的实数根 b2-4ac = 0 没有交点 没有实数根 b2-4ac < 0 ★二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次 方程ax2+bx+c=0根的关系 由前面的结论,我们可以利用二次函数的图象求一元二次方 程的根.由于作图或观察可能存在误差,由图象求得的根,一般 是近似的. -2 2 2 4 6 4-4 8 -2 -4 y = x2-2x-2解:画出函数y=x2-2x-2的图象 (如右图所示),它与x轴的公共 点的横坐标大约是-0.7,2.7. 所以方程x2-2x-2=0的实数根为 x1≈-0.7,x2≈2.7. 图象法解一元二次方程3 利用函数图象求方程x2-2x-2=0的 实数根(结果保留小数点后一位). 例 判断方程 ax2+bx+c =0 (a≠0,a、b、c为常数)一个解 x的范围是( ) A. 3< x < 3.23 B. 3.23 < x < 3.24 C. 3.24查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档