人教版数学八年级上册《三角形全等的判定》同步练习

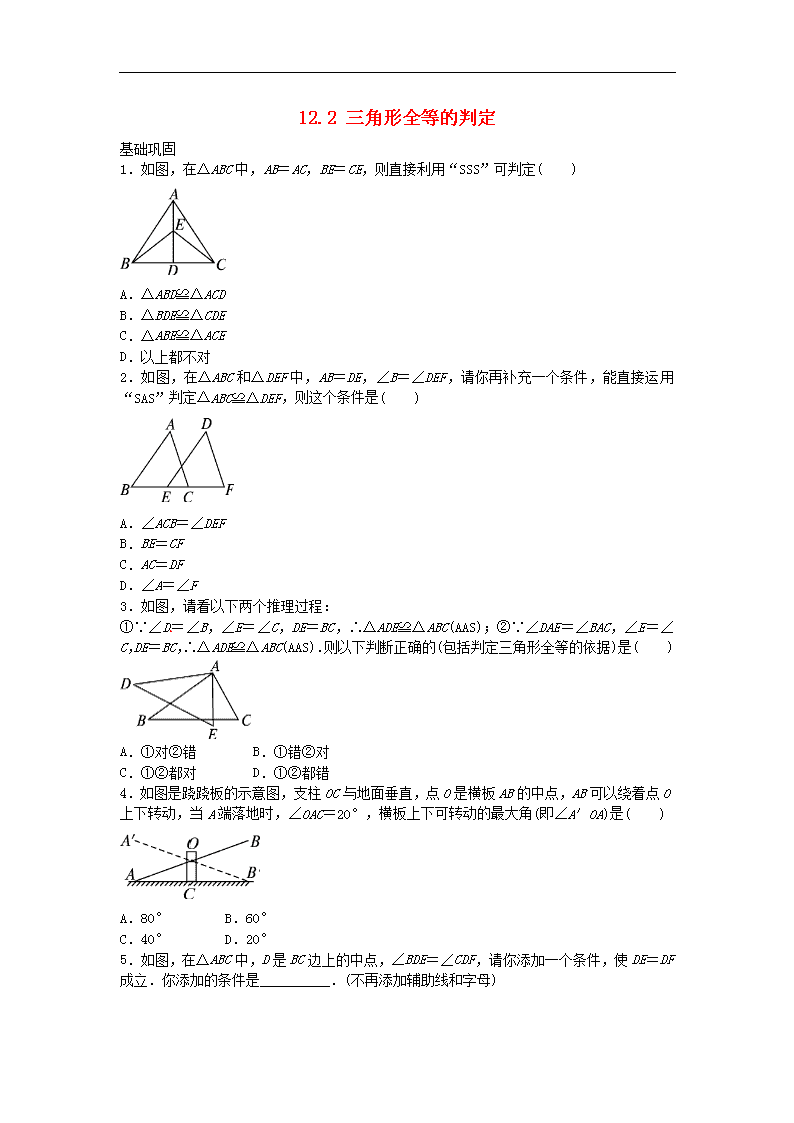
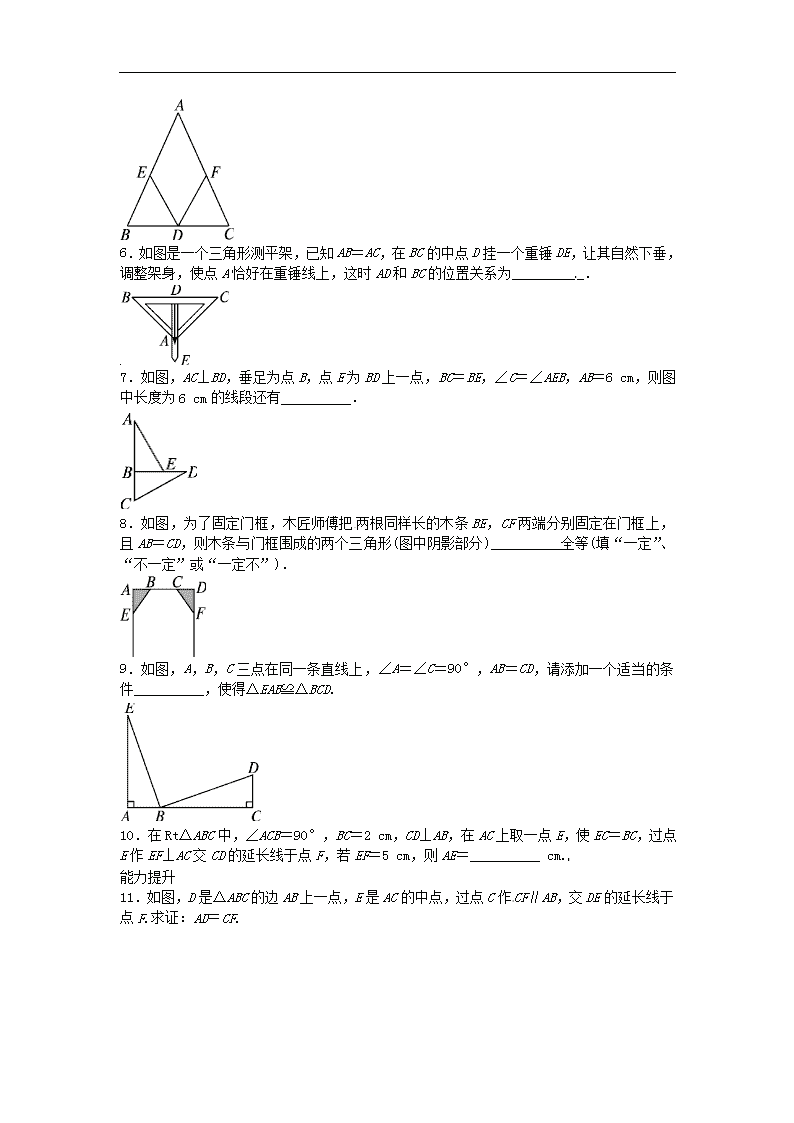
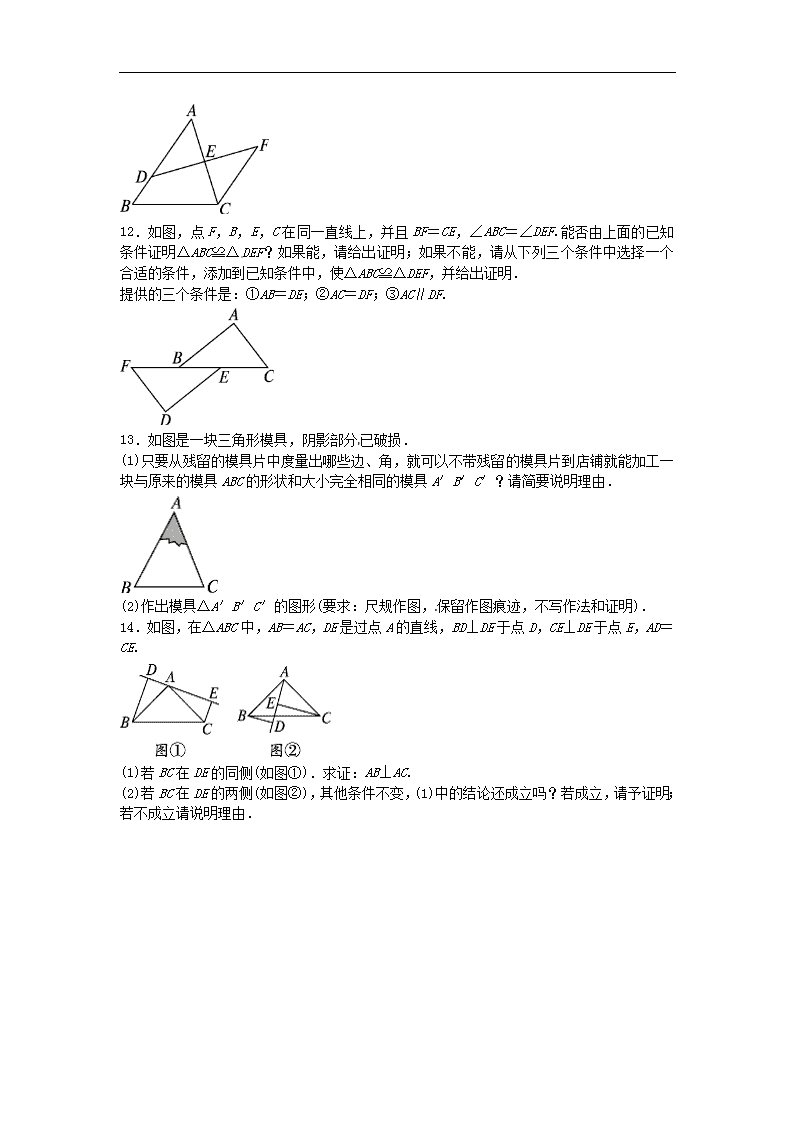
人教版数学八年级上册《三角形全等的判定》同步练习

12.2 三角形全等的判定 基础巩固 1．如图，在△ABC 中，AB＝AC，BE＝CE，则直接利用“SSS”可判定( ) A．△ABD≌△ACD B．△BDE≌△CDE C．△ABE≌△ACE D．以上都不对 2．如图，在△ABC 和△DEF 中，AB＝DE，∠B＝∠DEF，请你再补充一个条件，能直接运用“SAS” 判定△ABC≌△DEF，则这个条件是( ) A．∠ACB＝∠DEF B．BE＝CF C．AC＝DF D．∠A＝∠F 3．如图，请看以下两个推理过程： ①∵∠D＝∠B，∠E＝∠C，DE＝BC，∴△ADE≌△ABC(AAS)；②∵∠DAE＝∠BAC，∠E＝∠C， DE＝BC，∴△ADE≌△ABC(AAS)．则以下判断正确的(包括判定三角形全等的依据)是( ) A．①对②错 B．①错②对 C．①②都对 D．①②都错 4．如图是跷跷板的示意图，支柱 OC 与地面垂直，点 O 是横板 AB 的中点，AB 可以绕着点 O 上下转动，当 A 端落地时，∠OAC＝20°，横板上下可转动的最大角(即∠A′OA)是( ) A．80° B．60° C．40° D．20° 5．如图，在△ABC 中，D 是 BC 边上的中点，∠BDE＝∠CDF，请你添加一个条件，使 DE＝DF 成立．你添加的条件是__________．(不再添加辅助线和字母) 6．如图是一个三角形测平架，已知 AB＝AC，在 BC 的中点 D 挂一个重锤 DE，让其自然下垂， 调整架身，使点 A 恰好在重锤线上，这时 AD 和 BC 的位置关系为__________． 7．如图，AC⊥BD，垂足为点 B，点 E 为 BD 上一点，BC＝BE，∠C＝∠AEB，AB＝6 cm，则图 中长度为 6 cm 的线段还有__________． 8．如图，为了固定门框，木匠师傅把两根同样长的木条 BE，CF 两端分别固定在门框上， 且 AB＝CD，则木条与门框围成的两个三角形(图中阴影部分)__________全等(填“一定”、 “不一定”或“一定不”)． 9．如图，A，B，C 三点在同一条直线上，∠A＝∠C＝90°，AB＝CD，请添加一个适当的条 件__________，使得△EAB≌△BCD. 10．在 Rt△ABC 中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在 AC 上取一点 E，使 EC＝BC，过点 E 作 EF⊥AC 交 CD 的延长线于点 F，若 EF＝5 cm，则 AE＝__________ cm. 能力提升 11．如图，D 是△ABC 的边 AB 上一点，E 是 AC 的中点，过点 C 作CF∥AB，交 DE 的延长线于 点 F.求证：AD＝CF. 12．如图，点 F，B，E，C 在同一直线上，并且 BF＝CE，∠ABC＝∠DEF.能否由上面的已知 条件证明△ABC≌△ DEF？如果能，请给出证明；如果不能，请从下列三个条件中选择一个 合适的条件，添加到已知条件中，使△ABC≌△DEF，并给出证明． 提供的三个条件是：①AB＝DE；②AC＝DF；③AC∥DF. 13．如图是一块三角形模具，阴影部分 已破损． (1)只要从残留的模具片中度量出哪些边、角，就可以不带残留的模具片到店铺就能加工一 块与原来的模具 ABC 的形状和大小完全相同的模具 A′B′C′？请简要说明理由． (2)作出模具△A′B′C′的图形(要求：尺规作图，保留作图痕迹，不写作法和证明)． 14．如图，在△ABC 中，AB＝AC，DE 是过点 A 的直线，BD⊥DE 于点 D，CE⊥DE 于点 E，AD ＝CE. (1)若 BC 在 DE 的同侧(如图①)．求证：AB⊥AC. (2)若 BC 在 DE 的两侧(如图②)，其他条件不变，(1)中的结论还成立吗？若成立，请予证明； 若不成立请说明理由． 参考答案 1．C 点拨：因为 AB＝AC，BE＝CE，由图形知 AE＝AE，则直接利用“SSS”可判定△ABE≌ △ACE，故选 C. 2．B 点拨：若添加 BE＝CF，可得 BE＋EC＝CF＋EC，即 BC＝EF， 又因为 AB＝DE，∠B＝∠DEF，能直接运用“SAS”判定△ABC≌△DEF，故选 B. 3．B 点拨：因为①中的判定根据为 ASA，不是 AAS；②是正确的，故选 B. 4．C 点拨：因为点 O 是横板 AB 的中点，AB 可以绕着点 O 上下转动，所以 OB′＝OA，OC ＝OC，由 HL 得 Rt△OAC≌Rt△OB′C，得∠OB′C＝∠OAC＝20°，所以∠A′OA＝40°，故 选 C. 5．答案不唯一，如 AB＝AC 或∠B＝∠C 或∠BED＝∠CFD 或∠AED＝∠AFD. 点拨：答案不唯一．根据 AB＝AC，推出∠B＝∠C，根据 ASA 证出△BED 和△CFD 全等即可； 添加∠BED＝∠CDF，根据 AAS 即可推出△BED 和△CFD 全等；根据∠AED＝∠AFD 推出∠B＝ ∠C，根据 ASA 证△BED≌△CFD 即可． 6．垂直 点拨：由“边边边”可得△ADB≌△ADC，得∠ADB＝∠ADC，又因为∠ADB＋∠ADC ＝180°，∠ADB＝∠ADC＝90°，所以 AD 垂直于 BC. 7．BD 点拨：由 AC⊥BD，垂足为点 B，BC＝BE，∠C＝∠AEB，得△ABE≌△DBC，所以 BD＝ AB＝6 cm. 8．一定 点拨：由 HL 可证得△ABE≌△DCF. 9．AE＝CB(或 EB＝BD 或∠EBD＝90°或∠E＝∠DBC 等) 点拨 ：按 SAS 判定，需添加 AE＝ CB；按 ASA 判定，需添加∠ABE＝∠D；按 AAS 判定，需添加∠E＝∠DBC(或 BD⊥BE 或∠DBE ＝90°)； 按 HL 判定，需添加 EB＝BD. 10．3 点拨：根据直角三角形的两锐角互余的性质求出∠ECF＝∠B，然后利用“角边角” 证明△ABC 和△FCE 全等，根据全等三角形对应边相等可得 AC＝EF，再根据 AE＝AC－CE，代 入数据计算即可得解． 11．证明：∵E 是 AC 的中点，∴AE＝CE. ∵CF∥AB，∴∠A＝∠ECF，∠ADE＝∠F. 在△ADE 与△CFE 中， ADE F A ECF AE CE         ， ， ， ∴△ADE≌△CFE(AAS)． ∴AD＝CF. 12．解：由前面的已知条件不能证明△ABC≌△DEF.需要再添加条件①时：证明： ∵BF＝CE，∴EF＝BC，∵∠ABC＝∠DEF，AB＝DE，∴△ABC≌△DEF(SAS)． 添加条件③时，∵AC∥DF，∴∠ACB＝∠DFE，∴△ABC≌△DEF(ASA)． 13．解：(1)只要度量残留的三角形模具片的∠B，∠C 的度数和边 BC 的长即可． 根据“ASA”可证明△ABC≌△A′B′C′. (2)图略． 14．(1)证明：∵BD⊥DE，CE⊥DE， ∴∠ADB＝∠CEA＝90°，∠BAD＋∠ABD＝90°. 在 Rt△ADB 和 Rt△CEA 中， AB AC AD EC    ， ， ∴Rt△ADB≌Rt△CEA(HL)． ∴∠ABD＝∠CAE.∴∠BAD＋∠CAE＝90°， ∴∠BAC＝180°－(∠BAD＋∠CAE)＝90°，∴AB⊥AC. (2)解：仍有 AB⊥AC. 证明：∵BD⊥DE，CE⊥DE， ∴∠ADB＝∠CEA＝90°，∠BAD＋∠ABD＝90°. 在 Rt△ADB 和 Rt△CEA 中， AB CA AD CE    ， ，∴Rt△ADB≌Rt△CEA(HL)． ∴∠ABD＝∠CAE.∴∠BAD＋∠CAE＝90°， ∴∠BAC＝90°，∴AB⊥AC.