- 2021-05-24 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级数学上册第四章图形的相似4探索三角形相似的条件相似三角形的判定条件教学案无答案新版北师大版
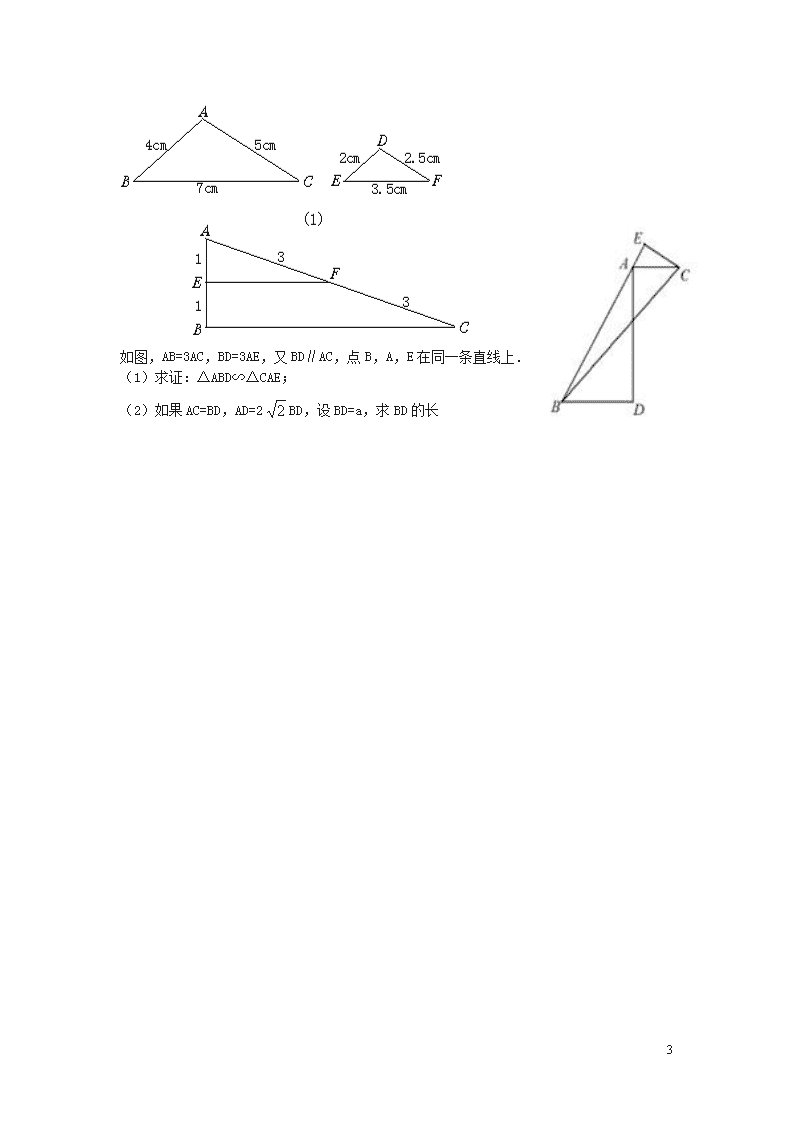
4.4.3相似三角形的判定条件 【教学目标】 知识与技能 初步掌握“三组对应边的比相等的两个三角形相似”的判定方法,能够运用三角形相似的条件解决简单的问题. 知道黄金分割的定义.会找一条线段的黄金分割点.并会判断某一点是否为一条线段的黄金分割点. 过程与方法 经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程. 情感、态度与价值观 通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性. 【教学重难点】 教学重点:三组对应边的比相等的两个三角形相似”的判定方法 教学难点:三组对应边的比相等的两个三角形相似”的判定方法 【导学过程】 【创设情景,引入新课】 复习两个三角形相似的判定方法1﹑2与全等三角形判定方法(AA﹑SAS)的区别与联系: 如果两个三角形的三组对应边的比相等,那么这两个三角形相似。 画△ABC与△A′B′C′,使、和都等于给定的值k。设法比 较∠A与∠A′的大小、∠B与∠B′的大小、∠C与∠C′的大小.△ABC与 △A′B′C′相似吗?说说你的理由。 相似三角形的判定方法2: 的两个三角形相似。 【自主探究】 下列三角形中,在△ABC中,AB= , AC= ,BC= ; 在△DEF中,DE= , DF= ,EF= ; 在△GMN中,GM= , GN= ,MN= . ∵ , , , ∵ , , , ∴ = . ∴ = . ∴ ∽ ∴ ∽ 3 结论归纳:通过以上计算和观察,你发现了什么结论? 如果两个三角形的三组 的比 ,那么这两个三角形 . 简单地说: 三边对应的比相等,两三角形相似. 用几何语言表示: ∵ = . ∵ = . ∴ ∽ ∴ ∽ ∴ ∽ 【课堂探究】 例3如图在△ABC和△ADE中 ∠BAD=20°求∠CAE的度数 在线段AB上,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割(golden section),点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.其中≈0.618. 【当堂训练】 1、如图4-32,△ABC与△A′B′C′相似吗?你有哪些判断方法? 图4-32 2、下面每组的两个三角形是否相似?为什么? 3 如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上. (1)求证:△ABD∽△CAE; (2)如果AC=BD,AD=2BD,设BD=a,求BD的长 3查看更多