云南中考数学等腰三角形特训方案知识梳理

云南中考数学等腰三角形特训方案知识梳理

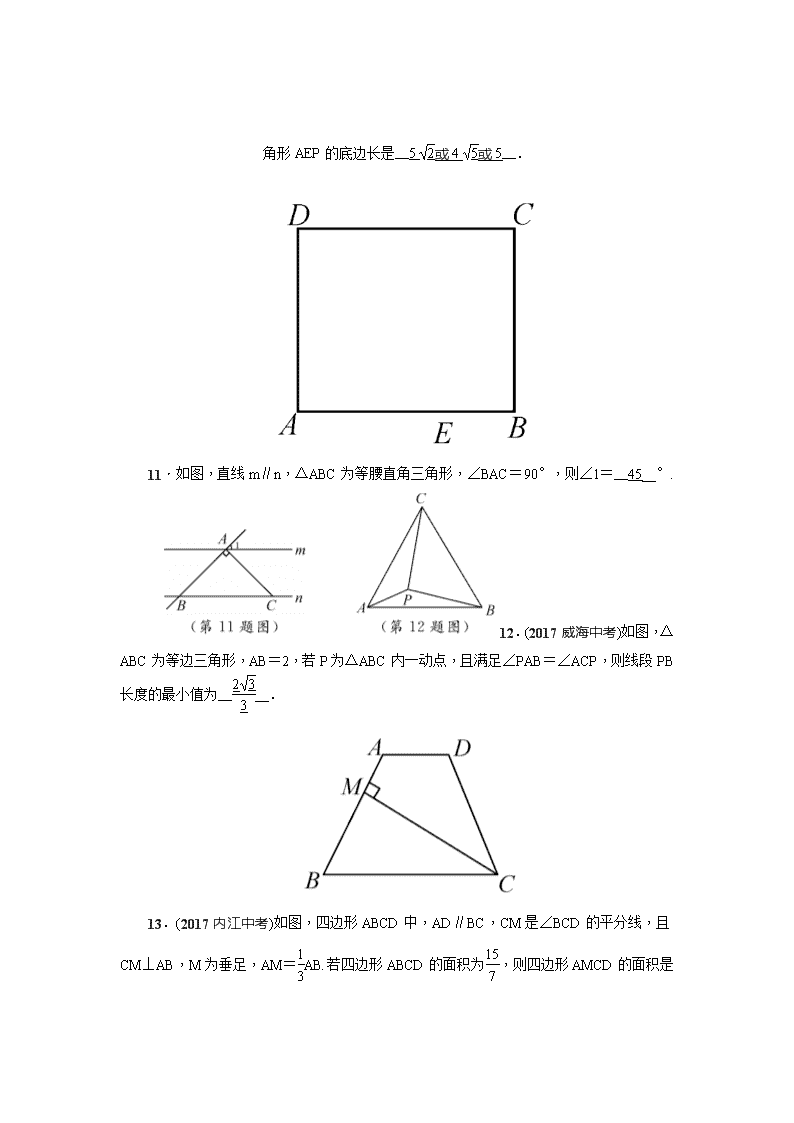
第15讲　等腰三角形 ‎ 　　　　　　 　　　　　 　　　　　‎ ‎1．如图①，在等腰三角形ABC中，AB＝AC＝4，BC＝7.如图②，在底边BC上取一点D，连接AD，使得∠DAC＝∠ACD.如图③，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连接BE，得到四边形ABED.则BE的长是(　B　) ‎ A．4 B. C．3 D．2 ‎2．已知实数x，y满足|x－4|＋＝0，则以x，y的值为两边长的等腰三角形的周长是(　C　)‎ A．20或16 B．16‎ C．20 D．以上答案均不对 ‎3．已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为(　B　)‎ A. B. C. D．不能确定 ‎4．如图，△ABC中，AB＝AC，AD是∠BAC的平分线．已知AB＝5，AD＝3，则BC的长为(　C　)‎ A．5 B．6 C．8 D．10‎ ‎5．(2017杭州中考)如图，在△ABC中，AB＝AC，BC＝12，E为AC边的中点，线段BE的垂直平分线交边BC于点D.设BD＝x，tan∠ACB＝y，则(　B　)‎ A．x－y2＝3 B．2x－y2＝9‎ C．3x－y2＝15 D．4x－y2＝21‎ ‎6．(2017南充中考)如图，等边△OAB的边长为2，则点B的坐标为(　D　)‎ A．(1，1) B．(，1) C．(，) D．(1，)‎ ‎7．(2017武汉中考)如图，在Rt△ABC中，∠C＝30°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为(　C　)‎ A．4 B．5 C. 6 D．7‎ ‎8．(2017荆州中考)如图，在△ABC中，AB＝AC, ∠A ＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为(　B　)‎ A．30° B．45° C．50° D．75°‎ ‎　　‎ ‎9．(2017无锡中考)如图，△ABC中，∠BAC＝90°，AB＝3，AC＝4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE，则线段CE的长等于(　D　)‎ A．2 B. C. D. ‎ ‎10．如图是一张长方形纸片ABCD，已知AB＝8，AD＝7，E为AB上一点，AE＝5，现要剪下一张等腰三角形纸片(△AEP)，使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是__5或4或5__．‎ ‎11．如图，直线m∥n，△ABC为等腰直角三角形，∠BAC＝90°，则∠1＝__45__°.‎ ‎12．(2017威海中考)如图，△ABC为等边三角形，AB＝2，若P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为____．‎ ‎13．(2017内江中考)如图，四边形ABCD中，AD∥BC，CM是∠BCD的平分线，且CM⊥AB，M为垂足，AM＝AB.若四边形ABCD的面积为，则四边形AMCD的面积是__1__.‎ ‎14．有一面积为5的等腰三角形，它的一个内角是30°，‎ 则以它的腰长为边的正方形的面积为__20或20__．‎ ‎15．(2017内江中考)如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC.‎ 求证：△BDE是等腰三角形．‎ ‎ ‎ 证明：∵DE∥AC，‎ ‎∴∠CAD＝∠ADE，‎ ‎∵AD平分∠BAC，‎ ‎∴∠CAD＝∠EAD，‎ ‎∴∠EAD＝∠ADE.‎ ‎∵AD⊥BD，‎ ‎∴∠EAD＋∠B＝90°，‎ ‎∴∠ADE＋∠BDE＝90°，‎ ‎∴∠B＝∠BDE，‎ ‎∴△BDE是等腰三角形．‎ ‎16．如图所示，在平面直角坐标系中，过点A(－，0)的两条直线分别交y轴于B，C两点，且B，C两点的纵坐标分别是一元二次方程x2－2x－3＝0的两个根．‎ ‎(1)求线段BC的长度；‎ ‎(2)试问：直线AC与直线AB是否垂直？请说明理由；‎ ‎(3)若点D在直线AC上，且DB＝DC，求点D的坐标．‎ 解：(1)∵x2－2x－3＝0，‎ ‎∴x＝3或x＝－1，‎ ‎∴B(0，3)，C(0，－1)，‎ ‎∴BC＝4；‎ ‎(2)垂直．理由如下：‎ ‎∵A(－，0)，B(0，3)，C(0，－1)，‎ ‎∴OA＝，OB＝3，OC＝1，‎ ‎∴OA2＝OB·OC.‎ ‎∵∠AOC＝∠BOA＝90°，‎ ‎∴△AOC∽△BOA，‎ ‎∴∠CAO＝∠ABO，‎ ‎∴∠CAO＋∠BAO＝∠ABO＋∠BAO＝90°，‎ ‎∴∠BAC＝90°，‎ ‎∴AC⊥AB；‎ ‎(3)设直线AC的解析式为y＝kx＋b，‎ 把A(－，0)和C(0，－1)代入y＝kx＋b，得 解得 ‎∴直线AC的解析式为y＝－x－1.‎ ‎∵DB＝DC，‎ ‎∴点D在线段BC的垂直平分线上，‎ ‎∴D的纵坐标为1.‎ 把y＝1代入y＝－x－1，得x＝－2，‎ ‎∴D的坐标为(－2，1)．‎