- 2021-05-24 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海教育版数学八下《一次函数的应用》同步练习
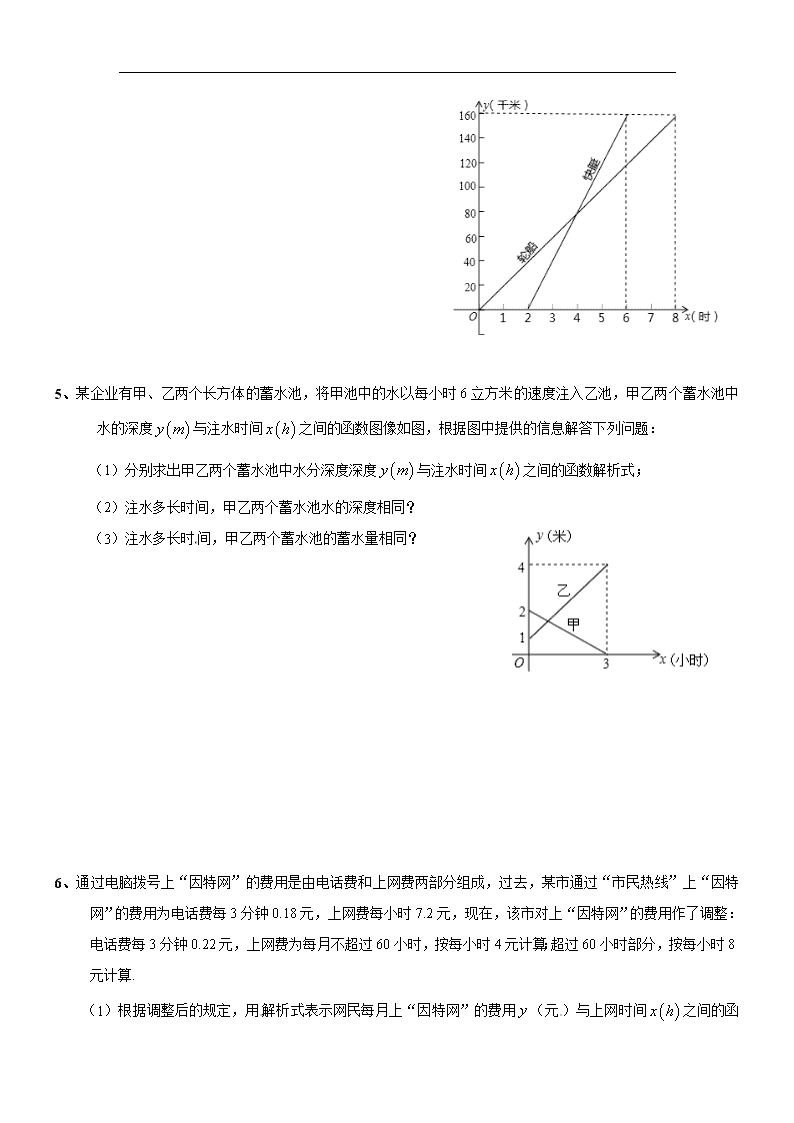
20.4 一次函数的应用 一、课本巩固练习 1、某种储蓄的月利率是 0.2%,如果存入 1000 元本金,不考虑利息 税, 且不急复利,求本息和 y 与所存月数 x 之前的函数解析式,并计算 6 个月后的本息和。 2、某长途汽车运输公司对乘客携带行李作如下规定:一个乘客可免费携带 30 千克行李,如果超过 30 千克,那 么超过部分每千克行李收行李费 1 元,设一个乘客的行李重量为 x 千克(x>30)试写出行李费 y(元)关于行李 重量 x(千克)的函数解析式及定义域,并画出函数图像。 3、张先生准备租一处临街房屋开一家电脑公司,现有甲乙两家房屋 出租,甲屋已装修好,每月租金 3000 元, 乙屋没有装修,每月租金 2000 元,但要装修成甲屋的模样,需要花费 4 万元,如果你是张先生,你会如何选择? 二、基础过关 1、一个水箱内有水 80 立方米,现要打开水箱的排水箱,以每小时排出的水量为 4 立方米进行排水. (1)表述水池中的剩余水量 3Q m 与排水时间 t h 之间的函数关系式; (2)在平面直角坐标系中画出这个函数的图像. 2、旅客乘车按规定可随身携带一定重量的行李,如果超过规定,那么需购买行李票,设行李费 y (元)是行李 重量 x kg 的函数,其图像如图所示. (1)求 y 与 x 之间的函数关系式; (2)旅客最多可免费携带行李的重量; (3)表述旅客所付的行李费 y (元)与他携带 的行李重量 x kg 之间的函数关系式. 3、某单位急需用车,但又不准备买车,他们和一个体车主或一国营出租车公司中的一家签订月租合同,设汽车 每月行驶 x 千米,应付给个体车主的月费用为 1y 元,应付给出租公司的月费用是 2y 元, 1y 、 2y 分别与 x 的函数图像(两条射线)如图,根据图中提供的信息解答下列问题: (1)每月行驶的路程在什么范围时,租国营公司的车合算? (2)每月行驶的路程等于多少时,租两家车的费用相同? (3)如果这个单位估计每月行驶的路程为 2300 千米, 那么这个单位租哪家划算? 4、一艘轮船和一艘快艇 沿相同的路线从甲港出发驶向乙港的过程中,路程 y km 随时间 x h 变化的图像如图 所示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题: (1)分别求出表示轮船和快艇行驶过程中路程 y km 和时间 x h 之间的函数解析式和定义域; (2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少? (3)快艇出发多长时间赶上轮船? 5、某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时 6 立方米的速度注入乙池,甲乙两个蓄水池中 水的深度 y m 与注水时间 x h 之间的函数图像如图,根据图中提供的信息解答下列问题: (1)分别求出甲乙两个蓄水池中水分深度深度 y m 与注水时间 x h 之间的函数解析式; (2)注水多长时间,甲乙两个蓄水池水的深度相同? (3)注水多长时间,甲乙两个蓄水池的蓄水量相同? [来 6、通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成,过去,某市通过“市民热线”上“因特 网”的费用为电话费每 3 分钟 0.18 元,上网费每小时 7.2 元,现在,该市对上“因特网”的费用作了调整: 电话费每 3 分钟 0.22 元,上网费为每月不超过 60 小时,按每小时 4 元计算;超过 60 小时部分,按每小时 8 元计算. (1)根据调整后的规定,用 解析式表示网民每月上“因特网”的费用 y (元 )与上网时间 x h 之间的函 数关系式; (2)资费调整前,网民小刚在其家庭经济预算中,一直有一笔每月 70 小时的上网费用支出,因“因特网” 资费调整后,小刚要想不超过其家庭经济预算中的上网费用支出,他现在每月至多可上网多少小时? (3)从资费调整前后该市网民上网费用的支出增减情况分析,哪些网民支出增加?哪些网民支出减少? 7、 某单位计划组织员工到 H 地旅游,人数估计在10 25 之间,甲乙两旅行社的服务质量相同,组织到 H 地旅游的价格都是每人 200 元,在洽谈时,甲旅行社表示可给予每位旅客七五折(即原价格的 75%)优 惠;乙旅行社表示可先免去一位旅客的旅游费用,其余旅客八折优惠. (1)该单位怎样选择,才能使其支付的旅游总费用较少? (2)若该单位的员工只能组成一个旅游队,且经核算选择甲旅行社比选择乙旅行社费用要便宜 1 46 , 则该单位参加旅游的员工有多少人? 8、 某医药研究所研制了一种抗生素新药,据临床观察:如果成人按规定的剂量注射这种抗生素,那么注射 药液后每毫升血液中的含药量 y g 与时间 t h 之间的关系近似地满足如图所示的折线. (1)写出注射药液后,每毫升血液中含药量 y g 与时间 t h 之间的函数解析式及自变量的取值范围; (2)据临床观察:每毫升血液中含药量不少于 4 g 时,对控制病情是有效的,如果病人按规定的剂量注射 该药液后,那么这一次注射的药液经过多长时间后控制病情开始有效?这个有效时间是多长?查看更多