- 2021-05-24 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁省大连市高考数学一模试卷文科解析
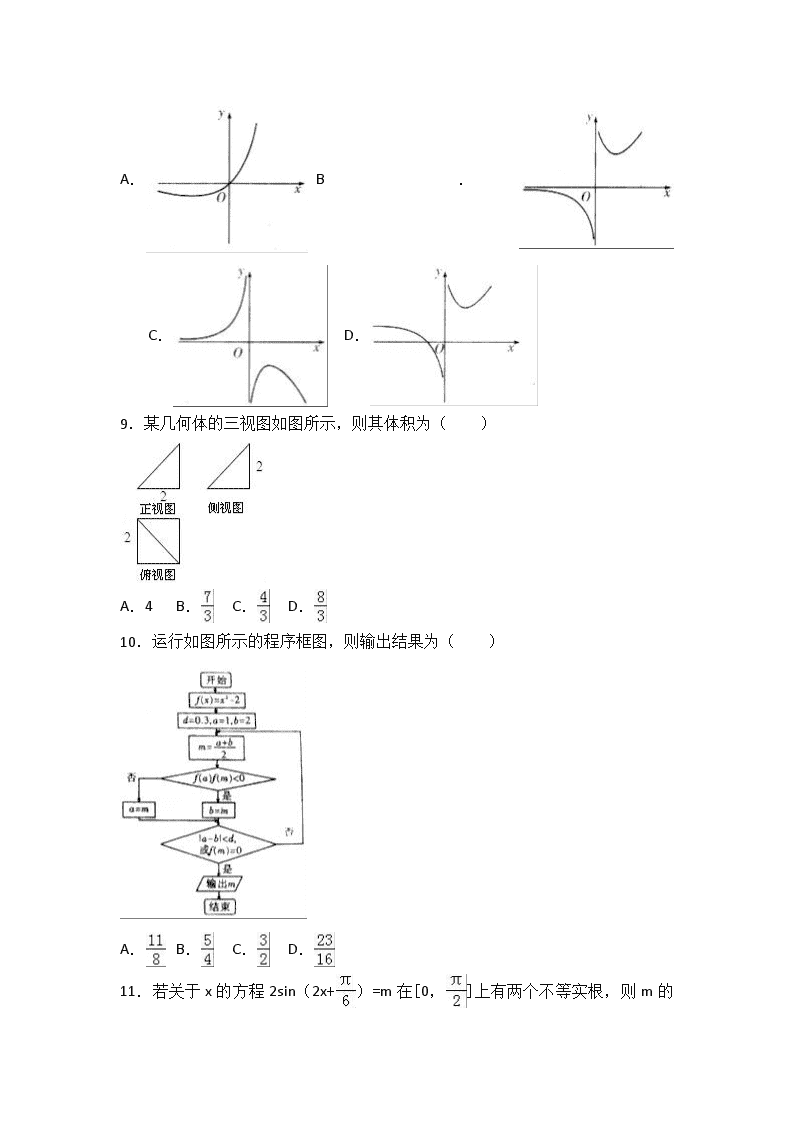
2017年辽宁省大连市高考数学一模试卷(文科) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数z=1+2i,则=( ) A.1﹣2i B.5+4i C.1 D.2 2.已知集合A={x|(x﹣3)(x+1)<0},B={x|x>1},则A∩B=( ) A.{x|x>3} B.{x|x>1} C.{x|﹣1<x<3} D.{x|1<x<3} 3.设a,b均为实数,则“a>b”是“a3>b3”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4.直线4x﹣3y=0与圆(x﹣1)2+(y﹣3)2=10相交所得弦长为( ) A.6 B.3 C. D. 5.下列命题中错误的是( ) A.如果平面α外的直线a不平行于平面α内不存在与a平行的直线 B.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ C.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β D.一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交 6.已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( ) A.9 B.15 C.18 D.30 7.在平面内的动点(x,y)满足不等式,则z=2x+y的最大值是( ) A.6 B.4 C.2 D.0 8.函数f(x)=的图象大致为( ) A. B. C. D. 9.某几何体的三视图如图所示,则其体积为( ) A.4 B. C. D. 10.运行如图所示的程序框图,则输出结果为( ) A. B. C. D. 11.若关于x的方程2sin(2x+)=m在[0,] 上有两个不等实根,则m的取值范围是( ) A.(1,) B.[0,2] C.[1,2) D.[1,] 12.已知定义在R上的函数f(x)为增函数,当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( ) A.(﹣∞,0) B. C.(,1) D.(1,+∞) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.某班级有50名同学,一次数学测试平均成绩是92,如果学号为1号到30号的同学平均成绩为90,则学号为31号到50号同学的平均成绩为 . 14.若函数f(x)=ex•sinx,则f'(0)= . 15.过双曲线﹣=1(a>0,b>0)的右焦点F且斜率为1的直线与渐近线有且只有一个交点,则双曲线的离心率为 . 16.我国古代数学专著《孙子算法》中有“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”如果此物数量在100至200之间,那么这个数 . 三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知点P(,1),Q(cosx,sinx),O为坐标原点,函数f(x)=•. (1)求函数f(x)的最小值及此时x的值; (2)若A为△ABC的内角,f(A)=4,BC=3,△ABC的面积为,求△ABC的周长. 18.某手机厂商推出一次智能手机,现对500名该手机使用者进行调查,对手机进行打分,打分的频数分布表如下: 女性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100) 频数 20 40 80 50 10 男性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100) 频数 45 75 90 60 30 (1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可); (2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率. 19.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点. (1)求证:PD⊥平面ABE; (2)求四棱锥P﹣ABCD外接球的体积. 20.已知函数f(x)=ax﹣lnx. (1)过原点O作函数f(x)图象的切线,求切点的横坐标; (2)对∀x∈[1,+∞),不等式f(x)≥a(2x﹣x2)恒成立,求实数a的取值范围. 21.已知椭圆Q: +y2=1(a>1),F1,F2分别是其左、右焦点,以线段F1F2为直径的圆与椭圆Q有且仅有两个交点. (1)求椭圆Q的方程; (2)设过点F1且不与坐标轴垂直的直线l交椭圆于A,B两点,线段AB的垂直平分线与x轴交于点P,点P横坐标的取值范围是[﹣,0),求|AB|的最小值. 四、请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程] 22.已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数). (1)求曲线C1的直角坐标方程及直线l的普通方程; (2)若曲线C2的参数方程为(α为参数),曲线C1上点P的极角为,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. [选修4-5:不等式选讲] 23.已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1. (1)求证:2a+b=2; (2)若a+2b≥tab恒成立,求实数t的最大值. 2017年辽宁省大连市高考数学一模试卷(文科) 参考答案与试题解析 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数z=1+2i,则=( ) A.1﹣2i B.5+4i C.1 D.2 【考点】复数的基本概念. 【分析】由已知直接利用共轭复数的概念得答案. 【解答】解:∵z=1+2i,∴=1﹣2i. 故选:A. 2.已知集合A={x|(x﹣3)(x+1)<0},B={x|x>1},则A∩B=( ) A.{x|x>3} B.{x|x>1} C.{x|﹣1<x<3} D.{x|1<x<3} 【考点】交集及其运算. 【分析】求出两个集合,然后求解交集即可. 【解答】解:A={x|(x﹣3)(x+1)<0}={x|﹣1<x<3}),B={x|x>1},则A∩B={x|1<x<3}, 故选:D 3.设a,b均为实数,则“a>b”是“a3>b3”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 【考点】必要条件、充分条件与充要条件的判断. 【分析】判断命题的真假:若a>b则a3>b3.是真命题,即a>b⇒a3>b3.若a3>b3则a>b.是真命题,即a3>b3⇒a>b. 【解答】解:若a>b则a3>b3.是真命题,即a>b⇒a3>b3. 若a3>b3则a>b.是真命题,即a3>b3⇒a>b. 所以a>b是a3>b3的充要条件. 故选:C. 4.直线4x﹣3y=0与圆(x﹣1)2+(y﹣3)2=10相交所得弦长为( ) A.6 B.3 C. D. 【考点】直线与圆的位置关系. 【分析】利用弦长公式|AB|=2,即可得出. 【解答】解:假设直线4x﹣3y=0与圆(x﹣1)2+(y﹣3)2=10相交所得弦为AB. 圆心到直线的距离d==1, ∴弦长|AB|=2=2=6. 故选:A. 5.下列命题中错误的是( ) A.如果平面α外的直线a不平行于平面α内不存在与a平行的直线 B.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ C.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β D.一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交 【考点】命题的真假判断与应用. 【分析】由空间中直线与平面的位置关系逐一核对四个选项得答案. 【解答】解:如果平面α外的直线a不平行于平面α,则a与α相交,则α内不存在与a平行的直线,故A正确; 如图:α⊥γ,α∩γ=a,β⊥γ,β∩γ=b,α∩β=l, 在γ内取一点P,过P作PA⊥a于A,作PB⊥b于B,由面面垂直的性质可得PA ⊥l,PB⊥l, 则l⊥γ,故B正确; 如果平面α⊥平面β,那么平面α内的直线与平面β有三种位置关系:平行、相交、异面,故C错误; 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交,故D正确. 故选:C. 6.已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( ) A.9 B.15 C.18 D.30 【考点】数列的求和. 【分析】利用等差数列的通项公式与求和公式可得an,Sn,对n分类讨论即可得出. 【解答】解:∵an+1﹣an=2,a1=﹣5,∴数列{an}是公差为2的等差数列. ∴an=﹣5+2(n﹣1)=2n﹣7. 数列{an}的前n项和Sn==n2﹣6n. 令an=2n﹣7≥0,解得. ∴n≤3时,|an|=﹣an. n≥4时,|an|=an. 则|a1|+|a2|+…+|a6|=﹣a1﹣a2﹣a3+a4+a5+a6=S6﹣2S3=62﹣6×6﹣2(32﹣6×3)=18. 故选:C. 7.在平面内的动点(x,y)满足不等式,则z=2x+y的最大值是( ) A.6 B.4 C.2 D.0 【考点】简单线性规划. 【分析】根据约束条件画出可行域,再利用几何意义求最值,只需求出直线z=x+ y的最优解,然后求解z最大值即可. 【解答】解:根据不等式,画出可行域, 由,可得x=3,y=0 平移直线2x+y=0,∴当直线z=2x+y过点A(3,0)时,z最大值为6. 故选:A. 8.函数f(x)=的图象大致为( ) A. B. C. D. 【考点】利用导数研究函数的单调性;函数的图象. 【分析】 利用函数的导数判断函数的单调性以及函数的值域,判断函数的图象即可. 【解答】解:函数f(x)=的定义域为:x≠0,x∈R,当x>0时,函数f′(x)=,可得函数的极值点为:x=1,当x∈(0,1)时,函数是减函数,x>1时,函数是增函数,并且f(x)>0,选项B、D满足题意. 当x<0时,函数f(x)=<0,选项D不正确,选项B正确. 故选:B. 9.某几何体的三视图如图所示,则其体积为( ) A.4 B. C. D. 【考点】由三视图求面积、体积. 【分析】通过三视图复原的几何体是正四棱锥,结合三视图的数据,求出几何体的体积. 【解答】解:由题意三视图可知,几何体是正四棱锥, 底面边长为2的正方形,一条侧棱垂直正方形的一个顶点,长度为2, 所以四棱锥的体积. 故选D. 10.运行如图所示的程序框图,则输出结果为( ) A. B. C. D. 【考点】程序框图. 【分析】由程序框图知,程序运行的功能是 用二分法求函数f(x)=x2﹣2在区间[1,2]上的零点,且精确到0.3; 模拟运行过程,即可得出结果. 【解答】解:由程序框图知,程序运行的功能是 用二分法求函数f(x)=x2﹣2在区间[1,2]上的零点,且精确到0.3; 模拟如下; m==时,f(1)•f()=(﹣1)×<0, b=,|a﹣b|=≥d; m==时,f(1)•f()=(﹣1)×(﹣)>0, a=,|a﹣b|=<d; 程序运行终止,输出m=. 故选:B. 11.若关于x的方程2sin(2x+)=m在[0,]上有两个不等实根,则m的取值范围是( ) A.(1,) B.[0,2] C.[1,2) D.[1,] 【考点】正弦函数的图象. 【分析】把方程2sin(2x+)=m化为sin(2x+)=,画出函数f(x)=sin(2x+)在x∈[0,]上的图象,结合图象求出方程有两个不等实根时m的取值范围. 【解答】解:方程2sin(2x+)=m可化为 sin(2x+)=, 当x∈[0,]时,2x+∈[,], 画出函数y=f(x)=sin(2x+)在x∈[0,]上的图象如图所示; 根据方程2sin(2x+)=m在[0,]上有两个不等实根, 得≤<1 1≤m<2 ∴m的取值范围是[1,2). 故选:C. 12.已知定义在R上的函数f(x)为增函数,当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( ) A.(﹣∞,0) B. C.(,1) D.(1,+∞) 【考点】函数单调性的性质. 【分析】根据题意,分析可得若不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则有,解可得实数x1的取值范围,即可得答案. 【解答】解:根据题意,若f(x1)+f(0)>f(x2)+f(1),则有f(x1)﹣f(x2)>f(1)﹣f(0), 又由x1+x2=1,则有f(x1)﹣f(1﹣x1)>f(1)﹣f(0), 又由函数f(x)为增函数, 则不等式f(x1)+f(0)>f(x2)+f(1)恒成立可以转化为, 解可得:x1>1,即实数x1的取值范围是(1,+∞); 故选:D. 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.某班级有50名同学,一次数学测试平均成绩是92,如果学号为1号到30号的同学平均成绩为90,则学号为31号到50号同学的平均成绩为 95 . 【考点】众数、中位数、平均数. 【分析】设学号为31号到50号同学的平均成绩为x,得到关于x的方程,解出即可. 【解答】解:设学号为31号到50号同学的平均成绩为x, 则92×50=90×30+20x,解得:x=95, 故答案为:95. 14.若函数f(x)=ex•sinx,则f'(0)= 1 . 【考点】导数的运算. 【分析】先求f(x)的导数,再求导数值. 【解答】解:f(x)=ex•sinx,f′(x)=(ex)′sinx+ex.(sinx)′=ex•sinx+ex•cosx,∴f'(0)=0+1=1 故答案为:1 15.过双曲线﹣=1(a>0,b>0)的右焦点F且斜率为1的直线与渐近线有且只有一个交点,则双曲线的离心率为 . 【考点】双曲线的简单性质. 【分析】根据双曲线的几何性质,所给直线应与双曲线的一条渐近线y=x平行,由此能求出双曲线的离心率. 【解答】解:∵经过双曲线﹣=1(a>0,b>0)的右焦点, 倾斜角为60°的直线与双曲线有且只有一个交点, ∴根据双曲线的几何性质,所给直线应与双曲线的一条渐近线y=x平行, ∴=1,∴, 解得e2=2,∴离心率e=. 故答案为:. 16.我国古代数学专著《孙子算法》中有“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”如果此物数量在100至200之间,那么这个数 128 . 【考点】数列的应用. 【分析】根据“三三数之剩二,五五数之剩三,七七数之剩二”找到三个数:第一个数能同时被3和5整除;第二个数能同时被3和7整除;第三个数能同时被5和7整除,将这三个数分别乘以被7、5、3除的余数再相加即可求出答案. 【解答】解:我们首先需要先求出三个数: 第一个数能同时被3和5整除,但除以7余1,即15; 第二个数能同时被3和7整除,但除以5余1,即21; 第三个数能同时被5和7整除,但除以3余1,即70; 然后将这三个数分别乘以被7、5、3除的余数再相加,即:15×2+21×3+70×2=233. 最后,再减去3、5、7最小公倍数的整数倍,可得:233﹣105×2=23.或105k+23(k为正整数). 由于物数量在100至200之间,故当k=1时,105+23=128 故答案为:128 三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知点P(,1),Q(cosx,sinx),O为坐标原点,函数f(x)=•. (1)求函数f(x)的最小值及此时x的值; (2)若A为△ABC的内角,f(A)=4,BC=3,△ABC的面积为,求△ABC的周长. 【考点】余弦定理;平面向量数量积的运算;正弦定理. 【分析】(1)根据向量的坐标运用求解,函数f(x)解析式,化解即可求函数f(x)的最小值及此时x的值. (2)由f(A)=4,BC=3,余弦定理和△ABC的面积为建立方程组,求解b,c的长度可得△ABC的周长. 【解答】解:(1)点P(,1),Q(cosx,sinx),O为坐标原点, =(,1),=(cosx,1﹣sinx) ∵函数f(x)=• ∴f(x)=3﹣cosx+1﹣sinx=4﹣2sin(x+) ∴当x=,k∈Z时,f(x)取得最小值2; (2)∵f(A)=4,即4﹣2sin(A+)=4 可得:A+=kπ,k∈Z. 0<A<π ∴A=. 又∵BC=3, 由余弦定理可得:a2=b2+c2﹣2bccos,即9=(b+c)2﹣bc. 又∵△ABC的面积为,即bcsinA=, 可得bc=3, 那么b+c=2 故得△ABC的周长为:a+b+c=2+3. 18.某手机厂商推出一次智能手机,现对500名该手机使用者进行调查,对手机进行打分,打分的频数分布表如下: 女性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100) 频数 20 40 80 50 10 男性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100) 频数 45 75 90 60 30 (1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可); (2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率. 【考点】列举法计算基本事件数及事件发生的概率;众数、中位数、平均数;极差、方差与标准差. 【分析】(Ⅰ)作出女性用户和男性用户的频率分布直方图,由图可得女性用户的波动小,男性用户的波动大. (Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,记为A,B,C,D,评分不小于90分分的人数为2,记为a,b,从6人人任取2人,利用列举法能求出两名用户评分都小于90分的概率. 【解答】解:(Ⅰ)女性用户和男性用户的频率分布直方图分别如下左、右图: 由图可得女性用户的波动小,男性用户的波动大. (Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人, 其中评分小于90分的人数为4,记为A,B,C,D, 评分不小于90分分的人数为2,记为a,b,从6人人任取2人, 基本事件空间为: Ω={(AB),(AC),(AD),(Aa),(Ab),(BC),(BD),(Ba),(Bb),(CD),(Ca),(Cb),(Da),(Db),(ab)},共有15个元素. 其中把“两名用户评分都小于90分”记作M, 则M={(AB),(AC),(AD),(BC),(BD),(CD)},共有6个元素. 所以两名用户评分都小于90分的概率为p=. 19.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点. (1)求证:PD⊥平面ABE; (2)求四棱锥P﹣ABCD外接球的体积. 【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定. 【分析】(1)推导出PA⊥AB,AB⊥AD,从而AB⊥平面PAD,进而AB⊥PD,再由AE⊥PD,能证明PD⊥平面ABE. (II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由此能求出四棱锥P﹣ABCD外接球的体积. 【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD, ∴PA⊥AB,又∵底面ABCD为矩形, ∴AB⊥AD,PA∩AD, 又PA⊂平面PAD,AD⊂平面PAD, ∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点, ∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE, ∴PD⊥平面ABE. 解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O, 由已知BD===4, 设C为BD中点,∴AM=2,OM=AP=1, ∴OA===3, ∴四棱锥P﹣ABCD外接球的体积是=36π. 20.已知函数f(x)=ax﹣lnx. (1)过原点O作函数f(x)图象的切线,求切点的横坐标; (2)对∀x∈[1,+∞),不等式f(x)≥a(2x﹣x2)恒成立,求实数a的取值范围. 【考点】导数在最大值、最小值问题中的应用;利用导数研究曲线上某点切线方程. 【分析】(1)通过设切点坐标,进而可写出切线方程,代入原点计算即得结论; (2)通过转化可知a(x2﹣x)≥lnx对∀x∈[1,+∞)恒成立,分别设y1 =a(x2﹣x),y2=lnx,利用x∈[1,+∞)可知a>0.再记g(x)=ax2﹣ax﹣lnx,通过举反例可知当0<a<1时不满足题意.进而转化为函数的最值问题,利用当x>1时lnx<x﹣1恒成立放缩即得结论. 【解答】解:(1)设切点为M(x0,f(x0)),直线的切线方程为y﹣f(x0)=k(x﹣x0), ∵f′(x)=a﹣,∴k=f′(x0)=a﹣, 即直线的切线方程为y﹣ax0+lnx0=(a﹣)(x﹣x0), 又切线过原点O,所以﹣ax0+lnx0=﹣ax0+1, 由lnx0=1,解得x0=e,所以切点的横坐标为e. (2)∵不等式ax﹣lnx≥a(2x﹣x2)恒成立, ∴等价于a(x2﹣x)≥lnx对∀x∈[1,+∞)恒成立. 设y1=a(x2﹣x),y2=lnx,由于x∈[1,+∞),且当a≤0时y1≤y2,故a>0. 记g(x)=ax2﹣ax﹣lnx, 则当0<a<1时,g(3)=6a﹣ln3≥0不恒成立,同理x取其他值不恒成立. 当x=1时,g(x)≥0恒成立; 当x>1时,则a≥恒成立,等价于问题转化为求h(x)=当x>1时的最大值. 又当x>1时,lnx<x﹣1<x(x﹣1),即h(x)=<1(x>1), 综上所述:a≥1. 21.已知椭圆Q: +y2=1(a>1),F1,F2分别是其左、右焦点,以线段F1F2为直径的圆与椭圆Q有且仅有两个交点. (1)求椭圆Q的方程; (2)设过点F1且不与坐标轴垂直的直线l交椭圆于A,B两点,线段AB的垂直平分线与x轴交于点P,点P横坐标的取值范围是[﹣,0),求|AB|的最小值. 【考点】圆锥曲线的最值问题;椭圆的标准方程. 【分析】(1)由题意可知c=b=1,由此能求出椭圆的方程. (2)设直线l方程为y=k(x+1),(k≠0),代入,得(1+2k2)x2+4k2x+2k2﹣2=0,由此利用中点坐标公式、韦达定理、线段垂直平分线方程、弦长公式,结合已知条件能求出|AB|的最小值. 【解答】(本小题满分12分) 解:(1)∵椭圆Q: +y2=1(a>1),F1,F2分别是其左、右焦点, 以线段F1F2为直径的圆与椭圆Q有且仅有两个交点, ∴由题意可知c=b=1, ∴a=,故椭圆的方程为. (2)设直线l方程为y=k(x+1),(k≠0), 代入,得(1+2k2)x2+4k2x+2k2﹣2=0, 设A(x1,y1),B(x2,y2),AB中点N(x0,y0), ∴,. ∴=﹣,, ∴AB的垂直平分线方程为y﹣y0=﹣, 令y=0,得, ∵,∴﹣,∴0<k2. |AB|=|x2﹣x1|=• =2 [], |AB|的最小值|AB|min=. 四、请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程] 22.已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数). (1)求曲线C1的直角坐标方程及直线l的普通方程; (2)若曲线C2的参数方程为(α为参数),曲线C1上点P的极角为,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. 【考点】简单曲线的极坐标方程;参数方程化成普通方程. 【分析】(1)曲线C1的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,可得直角坐标方程.直线l的参数方程为(t为参数),消去参数t可得普通方程. (2),直角坐标为(2,2),,利用点到直线的距离公式及其三角函数的单调性可得最大值. 【解答】解:(1)曲线C1的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ, 可得直角坐标方程:. 直线l的参数方程为(t为参数), 消去参数t可得普通方程:x+2y﹣3=0. (2),直角坐标为(2,2),, ∴M到l的距离≤, 从而最大值为. [选修4-5:不等式选讲] 23.已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1. (1)求证:2a+b=2; (2)若a+2b≥tab恒成立,求实数t的最大值. 【考点】函数恒成立问题;绝对值不等式的解法. 【分析】(1)法一:根据绝对值的性质求出f(x)的最小值,得到x=时取等号,证明结论即可;法二:根据f(x)的分段函数的形式,求出f(x)的最小值,证明即可; (2)法一,二:问题转化为≥t恒成立,根据基本不等式的性质求出的最小值,从而求出t的范围即可;法三:根据二次函数的性质判断即可. 【解答】解:(1)法一:f(x)=|x+a|+|2x﹣b|=|x+a|+|x﹣|+|x﹣|, ∵|x+a|+|x﹣|≥|(x+a)﹣(x﹣)|=a+且|x﹣|≥0, ∴f(x)≥a+,当x=时取等号,即f(x)的最小值为a+, ∴a+=1,2a+b=2; 法二:∵﹣a<,∴f(x)=|x+a|+|2x﹣b|=, 显然f(x)在(﹣∞,]上单调递减,f(x)在[,+∞)上单调递增, ∴f(x)的最小值为f()=a+, ∴a+=1,2a+b=2. (2)方法一:∵a+2b≥tab恒成立,∴≥t恒成立, =+=(+)(2a+b )•=(1+4++), 当a=b=时,取得最小值, ∴≥t,即实数t的最大值为; 方法二:∵a+2b≥tab恒成立, ∴≥t恒成立, t≤=+恒成立, +=+≥=, ∴≥t,即实数t的最大值为; 方法三:∵a+2b≥tab恒成立, ∴a+2(2﹣a)≥ta(2﹣a)恒成立, ∴2ta2﹣(3+2t)a+4≥0恒成立, ∴(3+2t)2﹣326≤0, ∴≤t≤,实数t的最大值为. 2017年4月15日查看更多