- 2021-05-24 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学第四章 三角形 周周测1(4-1) 北师大版
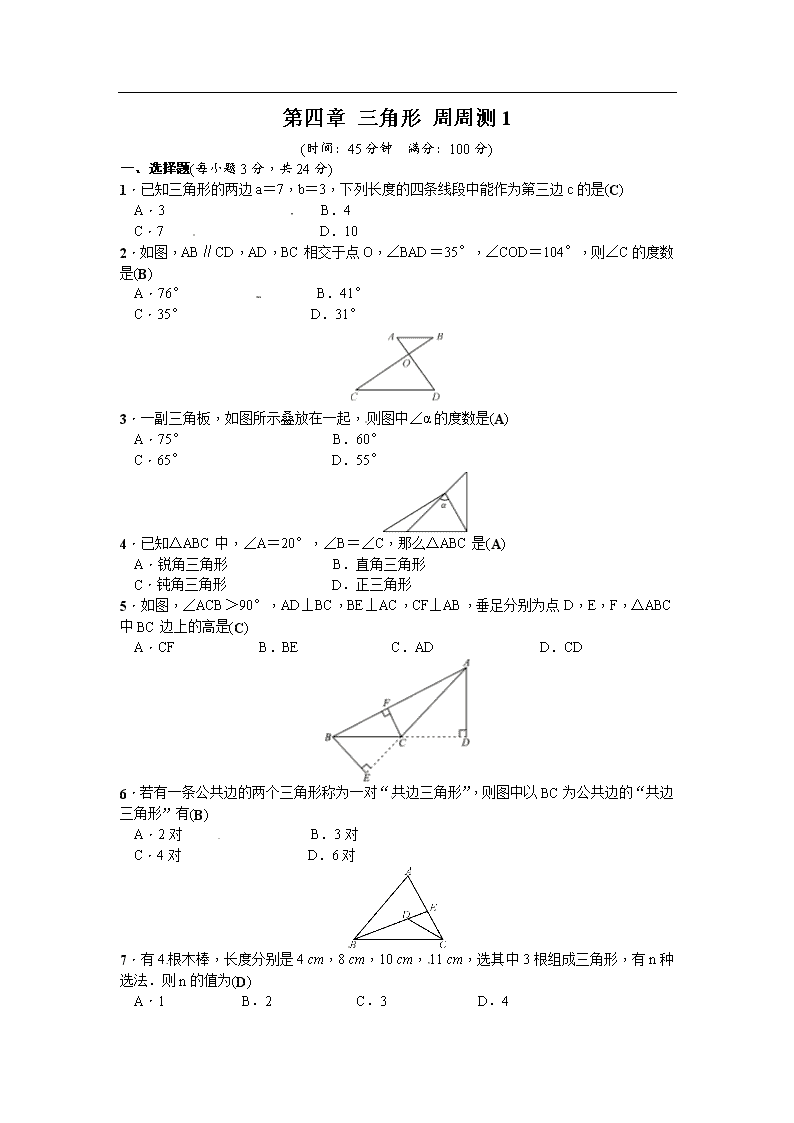
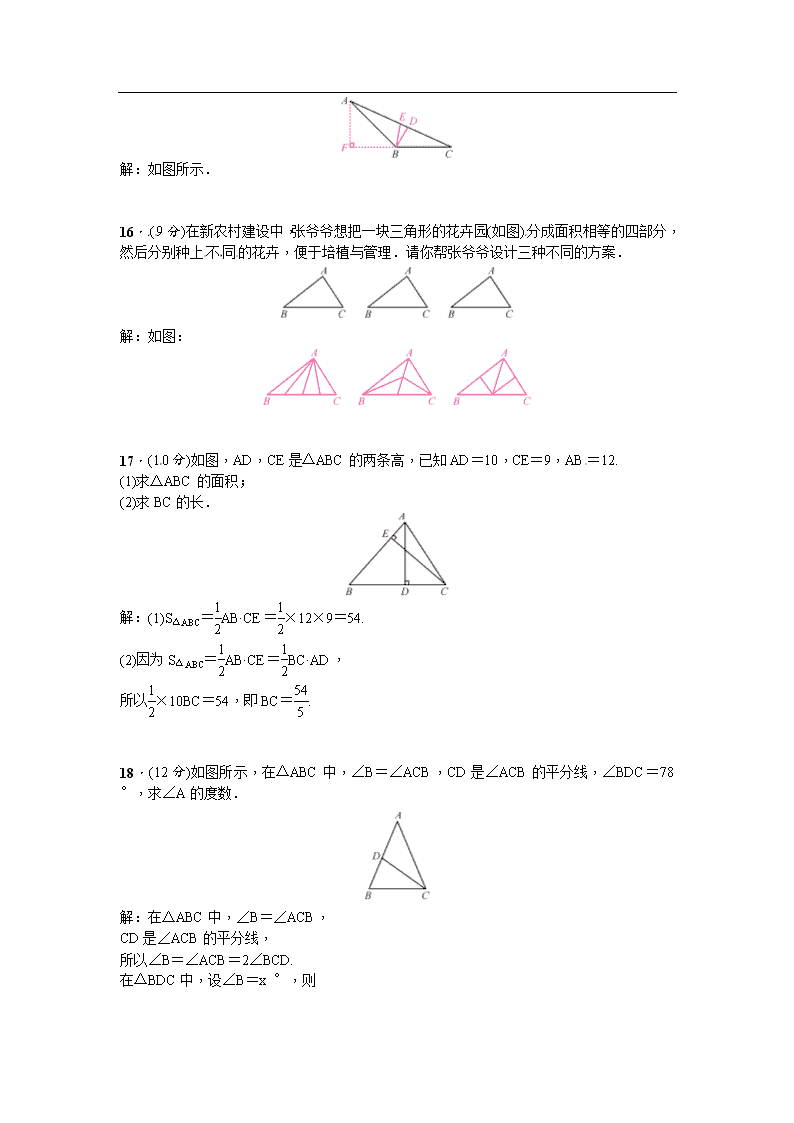
第四章 三角形 周周测1 (时间:45分钟 满分:100分) 一、选择题(每小题3分,共24分)[来源:学|科|网Z|X|X|K] 1.已知三角形的两边a=7,b=3,下列长度的四条线段中能作为第三边c的是(C)[来源:学§科§网] A.3 B.4 C.7 D.10 2.如图,AB∥CD,AD,BC相交于点O,∠BAD=35°,∠COD=104°,则∠C的度数是(B) A.76° B.41° C.35° D.31° 3.一副三角板,如图所示叠放在一起,则图中∠α的度数是(A) A.75° B.60° C.65° D.55° 4.已知△ABC中,∠A=20°,∠B=∠C,那么△ABC是(A) A.锐角三角形 B.直角三角形 C.钝角三角形 D.正三角形 5.如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D,E,F,△ABC中BC边上的高是(C) A.CF B.BE C.AD D.CD 6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有(B) A.2对 B.3对 C.4对 D.6对[来源:学科网] 7.有4根木棒,长度分别是4 cm,8 cm,10 cm,11 cm,选其中3根组成三角形,有n种选法.则n的值为(D) A.1 B.2 C.3 D.4 8.如图,CD,CE,CF分别是△ABC的高,角平分线、中线,则下列各式中错误的是(C) A.BA=2BF B.∠ACE=∠ACB C.AE=BE[来源:Z*xx*k.Com] D.CD⊥AB 二、填空题(每小题4分,共24分) 9.一个三角形有3条高,3条中线,3条角平分线. 10.如图,当BD=DC时,AD是△ABC的中线;当∠BAD=∠CAD时,AD是△ABC的角平分线. 11.如图,∠BAC=90°,AD⊥BC,∠BAD=30°,则∠C=30°. 12.(南充中考)如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度. 13.三角形中,一个内角α是另一个内角β的两倍时,我们称此三角形是“特征三角形”,其中α为“特征角”.如果一个“特征三角形”的“特征角”为110°,那么这个“特征三角形”的最小内角为15°. 14.如图,在△ABC中,点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8 cm2,则S△BEF=2cm2. [来源:Z_xx_k.Com] 三、解答题(共52分)[来源:学+科+网] 15.(9分)如图所示,在△ABC中,∠ABC是钝角,请画出: (1)∠ABC的平分线; (2)AC边上的中线; (3)BC边上的高. 解:如图所示. 16.(9分)在新农村建设中,张爷爷想把一块三角形的花卉园(如图)分成面积相等的四部分,然后分别种上不同的花卉,便于培植与管理.请你帮张爷爷设计三种不同的方案. 解:如图: [来源:学科网] 17.(10分)如图,AD,CE是△ABC的两条高,已知AD=10,CE=9,AB=12.[来源:学&科&网Z&X&X&K] (1)求△ABC的面积; (2)求BC的长. 解:(1)S△ABC=AB·CE=×12×9=54. (2)因为S△ABC=AB·CE=BC·AD, 所以×10BC=54,即BC=.[来源:Z_xx_k.Com] 18.(12分)如图所示,在△ABC中,∠B=∠ACB,CD是∠ACB的平分线,∠BDC=78°,求∠A的度数. 解:在△ABC中,∠B=∠ACB, CD是∠ACB的平分线, 所以∠B=∠ACB=2∠BCD. 在△BDC中,设∠B=x °,则 ∠BCD=(x) °. 所以x+x+78=180. 解得x=68. 所以在等腰三角形ABC中, ∠A=180 °-2×68 °=44 °. 19.(12分)如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数. 解:因为AE平分∠CAB,∠CAB=50 °,[来源:学&科&网Z&X&X&K] 所以∠CAE=∠CAB=×50 °=25 °. 因为AD⊥BC,∠C=60 °, 所以在△ACD中,∠CAD=180 °-90 °-60 °=30 °. 所以∠DAE=∠DAC-∠CAE=30 °-25 °=5 °. 在△AOB中,∠OAB=∠CAE=25 °, ∠OBA=∠ABC=×(180 °-50 °-60 °)=35 °. 所以∠BOA=180 °-(∠OBA+∠OAB)=180 °-(35 °+25 °)=120°. 因此,∠DAE和∠BOA的度数分别为5 °,120 °.查看更多