北师大中考数学复习专题解直角三角形和应用题

北师大中考数学复习专题解直角三角形和应用题

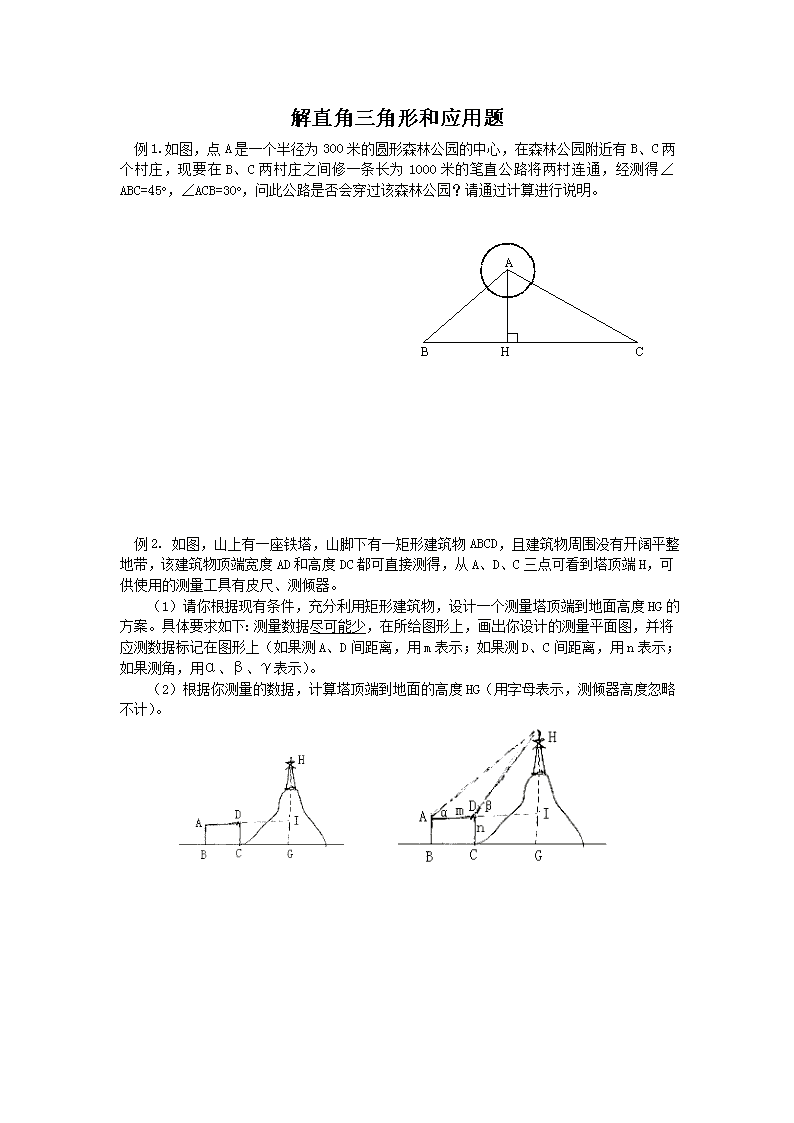
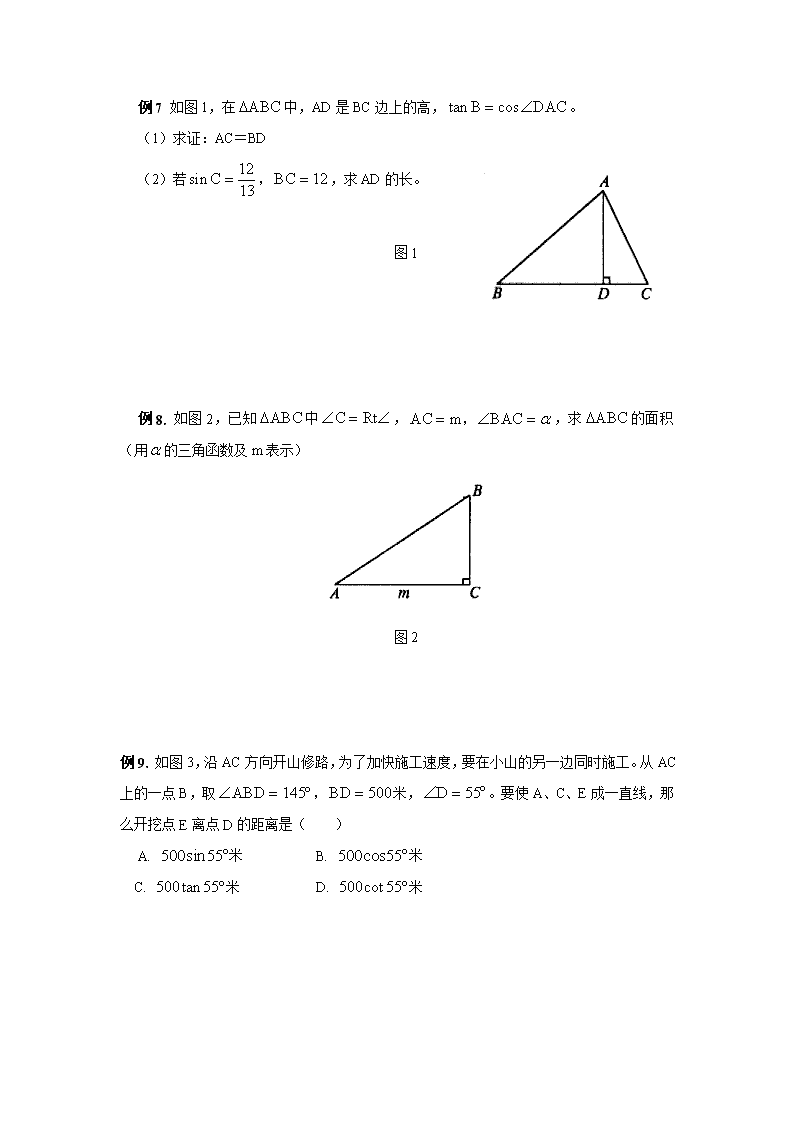
解直角三角形和应用题 ‎ 例1. 如图，点A是一个半径为300米的圆形森林公园的中心，在森林公园附近有B、C两个村庄，现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通，经测得∠ABC=45o，∠ACB=30o，问此公路是否会穿过该森林公园？请通过计算进行说明。‎ ‎ ‎ ‎ 例2. 如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有开阔平整地带，该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点可看到塔顶端H，可供使用的测量工具有皮尺、测倾器。‎ ‎ （1）请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG的方案。具体要求如下：测量数据尽可能少，在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上（如果测A、D间距离，用m表示；如果测D、C间距离，用n表示；如果测角，用α、β、γ表示）。‎ ‎ （2）根据你测量的数据，计算塔顶端到地面的高度HG（用字母表示，测倾器高度忽略不计）。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例3. 某一时刻，一架飞机在海面上空C点处观测到一人在海岸A点处钓鱼。从C点处测得A的俯角为45o；同一时刻，从A点处测得飞机在水中影子的俯角为60o。已知海岸的高度为4米，求此时钓鱼的人和飞机之间的距离（结果保留整数）。‎ ‎ ‎ 例4. 在中，，那么cotB等于（ ）‎ 例5 已知为锐角，下列结论：‎ ‎ <2>如果，那么 ‎<3>如果，那么 <4>‎ 正确的有（ ）‎ A. 1个 B. 2个 C. 3个 D. 4个 例6. （1）计算：‎ ‎（2）计算：‎ 例7 如图1，在中，AD是BC边上的高，。‎ ‎（1）求证：AC＝BD ‎（2）若，求AD的长。‎ 图1‎ 例8. 如图2，已知中，，求的面积（用的三角函数及m表示）‎ 图2‎ 例9. 如图3，沿AC方向开山修路，为了加快施工速度，要在小山的另一边同时施工。从AC上的一点B，取米，。要使A、C、E成一直线，那么开挖点E离点D的距离是（ ）‎ A. 米 B. 米 ‎ C. 米 D. 米 图3‎ 例10. 人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只正以24海里/小时的速度向正东方向航行。为迅速实验检查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问（1）需要几小时才能追上？（点B为追上时的位置）（2）确定巡逻艇的追赶方向（精确到）（如图4）‎ 图4‎ 参考数据：‎ 例11. 如图5，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有平整地带，该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点可看到塔顶端H，可供使用的测量工具有皮尺，测倾器。‎ 图5‎ ‎ 1. 测量底部不可以到达的物体的高度，可以按下列步骤进行：（如图所示，以测量MN的高度为例）‎ ‎ ①在测点A处安置测倾器，测得此时M的仰角。‎ ‎ ②在测点A与物体之间的B处安置测倾器（A、B与N在一条直线上），测得此时M的仰角。‎ ‎③量出测倾器的高度，以及测点 A、B之间的距离AB=b。‎ ‎（1）根据测量数据，你能求出物体MN的高度吗？‎ 说说你的理由。‎ ‎（2）若，‎ 试计算MN的高度。‎ ‎ 2. 公路MN和公路PQ在点P处交汇，且，点A处有一所中学，AP=160m，一辆拖拉机以3.6km/h的速度在公路MN上沿PN方向行驶，假设拖拉机行驶时，周围100m以内会受噪声影响，那么，学校是否会受到噪声影响？如果不受影响，请说明理由；如果受影响，会受影响几分钟？‎ ‎ 3. 某公司到果园基地购买某种优质水果，慰问医务工作者，果园基地对购买量在3000千克以上（含3000千克）的有两种销售方案。甲方案：每千克9元，由基地送货上门。乙方案：每千克8元，由顾客自己租车运回。已知该公司租车从基地到公司的运输费为5000元。‎ ‎ （1）分别写出该公司两种购买方案的付款y（元）与所购买的水果质量x（千克）之间的函数关系式，并写出自变量x的取值范围。‎ ‎（2）依据购买量判断，选择哪种购买方案付款最少？并说明理由。‎ ‎ 4. 某市从今年1月1日起调整居民用水价格，每立方米水费上涨1/3，小利家去年12月的水费是15元，而今年7月份的水费则是30元。已知小利家今年7月的用水量比去年12月份的用水量多5立方米，求该市今年居民的用水价格。‎