- 2021-05-23 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级数学上册第一章丰富的图形世界检测题新版北师大版
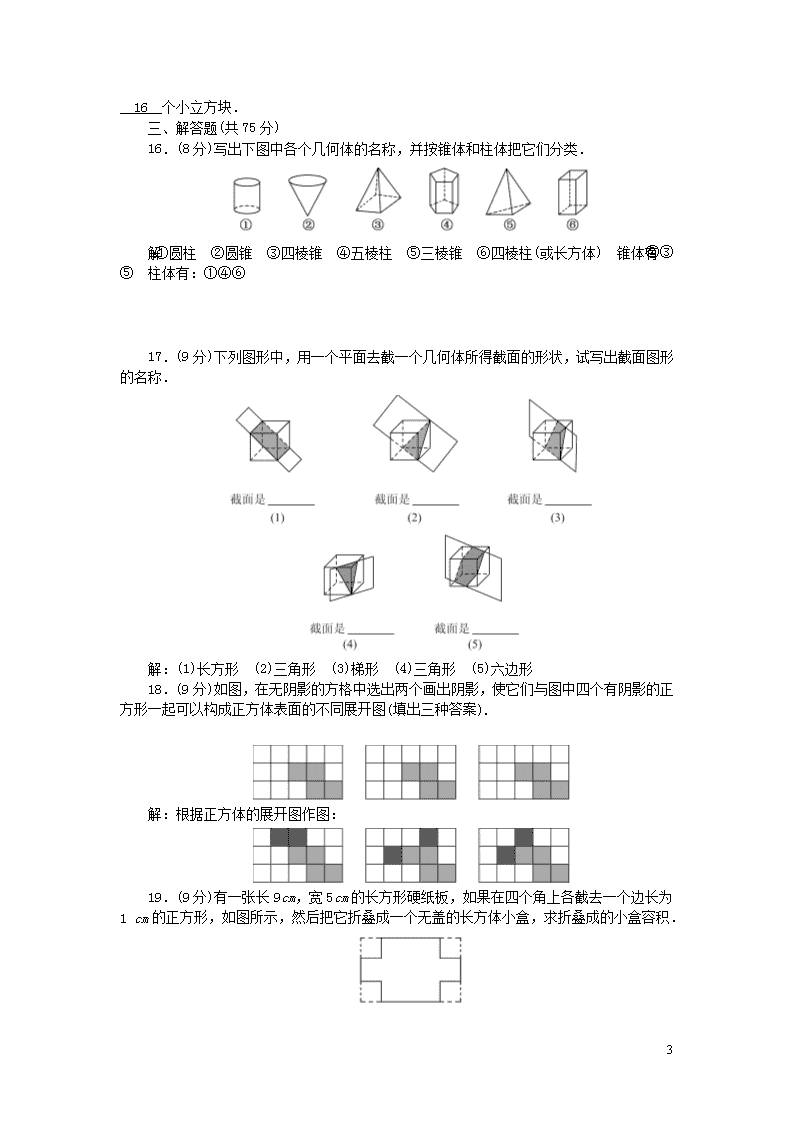
第一章 丰富的图形世界检测题 (时间:100分钟 满分:120分) 一、选择题(每小题3分,共30分) 1.下列各几何体中,直棱柱的个数是( C ) A.5个 B.4个 C.3个 D.2个 2.下列说法中,正确的个数有( D ) ①长方体、正方体都是棱柱;②圆锥和圆柱的底面都是圆;③若棱柱的底面边长相等,则它的各个侧面面积相等;④棱锥底面边数与侧棱数相等;⑤直棱柱的上、下底面是形状、大小相同的多边形,侧面都是长方形. A.2个 B.3个 C.4个 D.5个 3.(长沙中考)将下列左图的平面图形绕轴l旋转一周,可以得到的立体图形是( D ) 4.用一个平面去截一个正方体,截面的形状不可能是( D ) A.梯形 B.五边形 C.六边形 D.七边形 5.一个正方体的每个面都有一个汉字,其平面展开图如图所示,在该正方体中,和“国”字相对的字是( B ) A.武 B.汉 C.加 D.油 6.(永州中考)某同学家买了一个外形非常接近球的西瓜,该同学将西瓜均匀切成了8块,并将其中一块(经抽象后)按如图所示的方式放在自已正前方的水果盘中,则这块西瓜从三个不同方向看的图形( B ) 5 7.(大庆中考)一个“粮仓”从三个方向看得到的形状图如图所示(单位:m),则它的体积是( C ) A.21π m3 B.30π m3 C.45π m3 D.63π m3 8.(宁夏中考)如图是由几个小立方块所搭成的几何体从上面看到的图形,小正方形中的数字表示在该位置小立方块的个数,则这个几何体从正面看到的图形是( A ) 9.(济宁中考)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( B ) 10.(宜宾中考)已知一个几何体是由几个相同的正方体叠合在一起组成,该几何体从正面和上面看到的图形如图所示,则该几何体中正方体的个数最多是( B ) A.10 B.9 C.8 D.7 二、填空题(每小题3分,共15分) 11.四棱锥共有五个面,其中底面是四边形,侧面都是三角形. 12.(攀枝花中考)如图是一个多面体的表面展开图(图中字母在外表面上),如果面F在前面,从左面看是面B,那么从上面看是面__C__.(填字母) 13.如图所示,圆柱体的高为8,底面半径为2,则截面面积最大为32. 14.如果五棱柱的底面边长都是2 cm,侧棱长都是4 cm,那么它所有棱长的和是40 cm,它的侧面展开图的面积是40 cm2. 15.(青岛中考) 5 如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走__16__个小立方块. 三、解答题(共75分) 16.(8分)写出下图中各个几何体的名称,并按锥体和柱体把它们分类. 解:①圆柱 ②圆锥 ③四棱锥 ④五棱柱 ⑤三棱锥 ⑥四棱柱(或长方体) 锥体有:②③⑤ 柱体有:①④⑥ 17.(9分)下列图形中,用一个平面去截一个几何体所得截面的形状,试写出截面图形的名称. 解:(1)长方形 (2)三角形 (3)梯形 (4)三角形 (5)六边形 18.(9分)如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成正方体表面的不同展开图(填出三种答案). 解:根据正方体的展开图作图: 19.(9分)有一张长9 cm,宽5 cm的长方形硬纸板,如果在四个角上各截去一个边长为1 cm的正方形,如图所示,然后把它折叠成一个无盖的长方体小盒,求折叠成的小盒容积. 5 解:小盒容积为(9-1×2)×(5-1×2)×1=7×3×1=21(cm3) 20.(9分)如图是某个几何体的三种形状图. (1)说出这个几何体的名称; (2)画出它的一种表面展开图. (1)这个几何体是三棱柱 (2)它的一种表面展开图如图所示 21.(10分)在平整的地面上,有若干个棱长完全相同的小正方体堆成的一个几何体,如图所示. (1)请画出这个几何体从三个方向看到的图形; (2)若现在你还有一些相同的小正方体,如果保持从上面看到的图形和从左面看到的图形不变,最多可以再添加几个小正方体? 解:(1) (2)最多可以再添加4个小正方体 22.(10分)用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示. (1)这样的几何体只有一种吗?它至少需要多少个小立方块?最多需要多少个小立方块? (2)画出这两种情况下的从左面看到的图形. 5 解:(1)不止一种,它至少需要10个小立方块,至多需要13个小立方块 (2)如图(答案不唯一) 23.(11分)我们曾学过圆柱的体积计算公式:V=Sh=πr2h(r是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2 cm,宽为1 cm,以它的一边所在的直线为轴旋转一周. (1)请画出所有情况的旋转方式的示意图; (2)根据(1)中所画情况计算出各种旋转方式所得到的几何体的体积是多少? 解:(1)如图所示: (2)①当以长方形的宽所在的直线为轴旋转时,如图①所示,得到的圆柱的底面半径为2 cm,高为1 cm,所以其体积是V1=π×22×1=4π(cm3);②当以长方形的长所在的直线为轴旋转时,如图②所示,得到的圆柱的底面半径为1 cm,高为2 cm,所以其体积是V2=π×12×2=2π(cm3),所以得到的几何体的体积是4π cm3或2π cm3 5查看更多