2020_2021学年新教材高中数学第一章空间向量与立体几何1

2020_2021学年新教材高中数学第一章空间向量与立体几何1

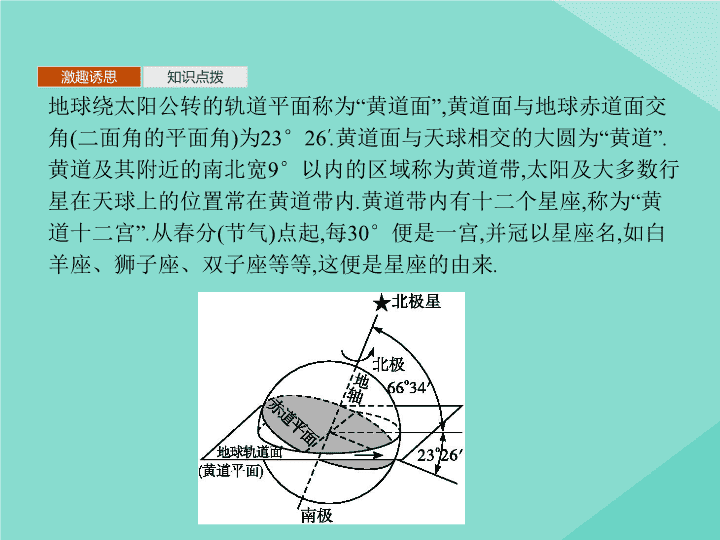
第 2 课时　利用向量求空间角 激趣诱思 知识点拨 地球绕太阳公转的轨道平面称为 “ 黄道面 ”, 黄道面与地球赤道面交角 ( 二面角的平面角 ) 为 23 ° 26 ' . 黄道面与天球相交的大圆为 “ 黄道 ” . 黄道及其附近的南北宽 9 ° 以内的区域称为黄道带 , 太阳及大多数行星在天球上的位置常在黄道带内 . 黄道带内有十二个星座 , 称为 “ 黄道十二宫 ” . 从春分 ( 节气 ) 点起 , 每 30 ° 便是一宫 , 并冠以星座名 , 如白羊座、狮子座、双子座等等 , 这便是星座的由来 . 激趣诱思 知识点拨 一、利用向量方法求两条异面直线所成的 角 名师点析 不要将两异面直线所成的角与其方向向量的夹角等同起来 , 因为两异面直线所成角的范围 是 , 而两个向量夹角的范围是 [0, π ], 事实上 , 两异面直线所成的角与其方向向量的夹角是相等或互补的关系 . 激趣诱思 知识点拨 微练习 若异面直线 l 1 , l 2 的方向向量分别是 a = (0, - 2, - 1), b = (2,0,4), 则异面直线 l 1 与 l 2 的夹角的余弦值等于 ( 　　 ) 答案 : B 　 激趣诱思 知识点拨 二、利用向量方法求直线与平面所成的角 直线 AB 与平面 α 相交于点 B , 设直线 AB 与平面 α 所成的角为 θ , 直线 AB 的方向向量为 u , 平面 α 的法向量为 n , 则 名师点析 1 . 直线与平面所成的角是指这条直线与它在这个平面内的射影所成的角 , 其范围是 激趣诱思 知识点拨 微练习 若直线 l 的方向向量与平面 α 的法向量的夹角等于 120 ° , 则直线 l 与平面 α 所成的角等于 ( 　　 ) A.120 ° B.60 ° C.150 ° D.30 ° 答案 : D 　 解析 : 因为直线 l 的方向向量与平面 α 的法向量的夹角等于 120 ° , 所以它们所在直线的夹角为 60 ° , 则直线 l 与平面 α 所成的角 等于 90 ° - 60 ° = 30 ° . 激趣诱思 知识点拨 三、利用向量方法求两个平面的夹角 1 . 平面 α 与平面 β 的夹角 : 平面 α 与平面 β 相交 , 形成四个二面角 , 我们把这四个二面角中不大于 90 ° 的二面角称为平面 α 与平面 β 的夹角 . 2 . 若平面 α , β 的法向量分别是 n 1 和 n 2 , 则平面 α 与平面 β 的夹角即为向量 n 1 和 n 2 的夹角或其补角 , 设平面 α 与平面 β 的夹角为 θ , 则 2 . 因为两个平面法向量的方向不确定 , 故 < n 1 , n 2 > ∈ (0, π ), 若 < n 1 , n 2 > 为钝角 , 应取其补角 . 激趣诱思 知识点拨 A.120 ° B.30 ° C.60 ° D.30 ° 或 150 ° 答案 : B 　 探究一 探究二 探究三 素养形成 当堂检测 利用向量方法求两异面直线所成角 例 1 如图所示 , 在三棱柱 ABC-A 1 B 1 C 1 中 , AA 1 ⊥ 底面 ABC , AB=BC=AA 1 , ∠ ABC= 90 ° , 点 E , F 分别是棱 AB , BB 1 的中点 , 试求直线 EF 和 BC 1 所成的角 . 思路分析 建立空间直角坐标系 , 求出直线 EF 和 BC 1 的方向向量的坐标 , 求它们的夹角即得直线 EF 和 BC 1 所成的角 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 1 . 利用空间向量求两异面直线所成角的步骤 . (1) 建立适当的空间直角坐标系 . (2) 求出两条异面直线的方向向量的坐标 . (3) 利用向量的夹角公式求出两直线方向向量的夹角 . (4) 结合异面直线所成角的范围得到两异面直线所成角 . 2 . 求两条异面直线所成的角的两个关注点 . (1) 余弦值非负 : 两条异面直线所成角的余弦值一定为非负值 , 而对应的方向向量的夹角可能为钝角 . (2) 范围 : 异面直线所成角的范围 是 , 故两直线方向向量夹角的余弦值为负时 , 应取其绝对值 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 1 如图 , 在正四棱柱 ABCD-A 1 B 1 C 1 D 1 中 , AA 1 = 2 AB , 则异面直线 A 1 B 与 AD 1 所成角的余弦值为 　　　　　 .   探究一 探究二 探究三 素养形成 当堂检测 利用向量方法求直线与平面所成角 例 2 如 图所示 , 四棱锥 P-ABCD 中 , PA ⊥ 底面 ABCD , AD ∥ BC , AB=AD=AC= 3, PA=BC= 4, M 为线段 AD 上一点 , AM= 2 MD , N 为 PC 的中点 . (1) 证明 MN ∥ 平面 PAB ; (2) 求直线 AN 与平面 PMN 所成角的正弦值 . 思路分析 (1) 线面平行的判定定理 ⇒ MN ∥ 平面 PAB. (2) 利用空间向量计算平面 PMN 与 AN 方向向量的夹角 ⇒ 直线 AN 与平面 PMN 所成角的正弦值 . 探究一 探究二 探究三 素养形成 当堂检测 又 AD ∥ BC , 故 TN