2012高考数学复习最新3年高考2年模拟函数与导数
【3 年高考 2 年模拟】第二章函数与导数
三年高考荟萃 2011 年高考题
一、选择题
1.(安徽理 3) 设 ( )f x 是定义在 R 上的奇函数,当 x 时, ( )f x x x
,则 ( )f
(A) (B) (C)1 (D)3
【答案】A
【命题意图】本题考查函数的奇偶性,考查函数值的求法.属容易题.
【解析】 2(1) ( 1) [2( 1) ( 1)] 3f f .故选 A.
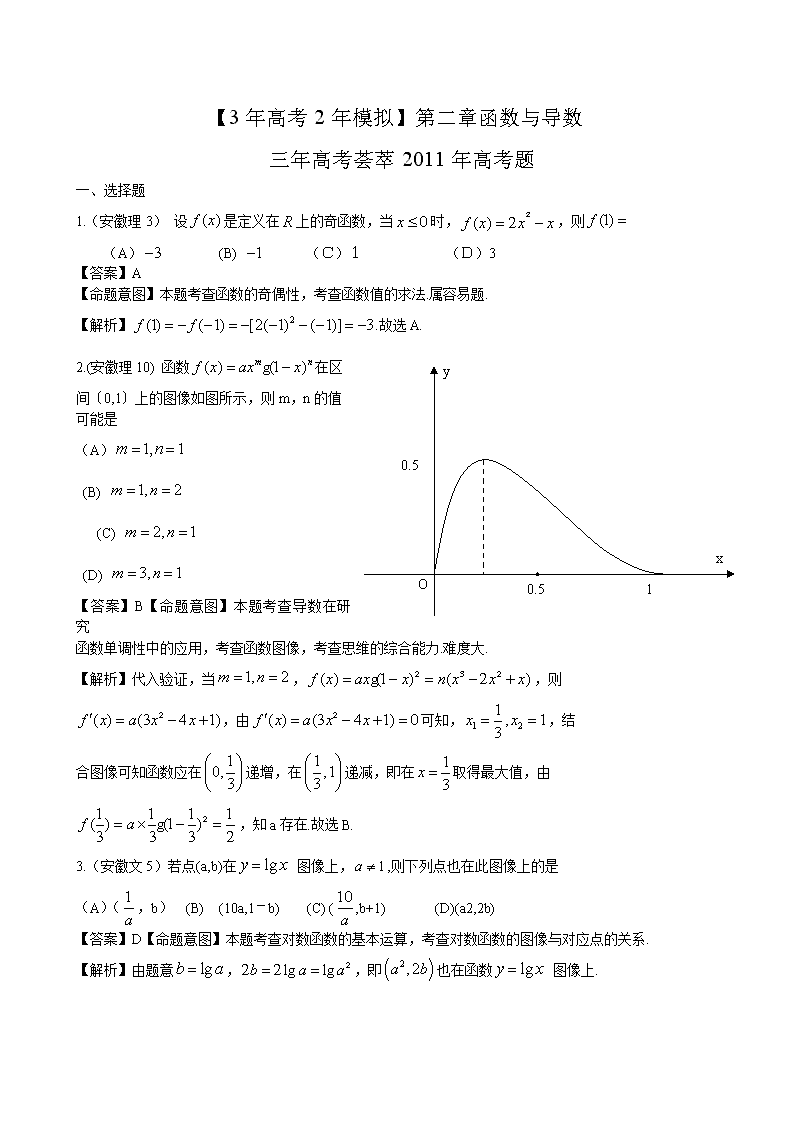
2.(安徽理 10) 函数 ( ) ( )m nf x ax x g 在区
间〔0,1〕上的图像如图所示,则 m,n 的值
可能是
(A) 1, 1m n
(B) 1, 2m n
(C) 2, 1m n
(D) 3, 1m n
【答案】B【命题意图】本题考查导数在研究
函数单调性中的应用,考查函数图像,考查思维的综合能力.难度大.
【解析】代入验证,当 1, 2m n , ( ) ( ) ( )f x ax x n x x x g ,则
( ) ( )f x a x x ,由 ( ) ( )f x a x x 可知, 1 2
1 , 13x x ,结
合图像可知函数应在 10, 3
递增,在 1 ,13
递减,即在 1
3x 取得最大值,由
( ) ( )f a g ,知 a 存在.故选 B.
3.(安徽文 5)若点(a,b)在 lgy x 图像上, a ,则下列点也在此图像上的是
(A)(
a
,b) (B) (10a,1 b) (C) (
a
,b+1) (D)(a2,2b)
【答案】D【命题意图】本题考查对数函数的基本运算,考查对数函数的图像与对应点的关系.
【解析】由题意 lgb a , lg lgb a a ,即 2 ,2a b 也在函数 lgy x 图像上.
y
0.5 1
x
O
0.5
4.(安徽文 10) 函数 ( ) ( )nf x ax x g 在
区间〔0,1〕上的图像如图所示,则 n 可
能是
(A)1 (B) 2
(C) 3 (D) 4
【答案】A【命题意图】本题考查导数在
研究函数单调性中的应用,考查函数图像,
考查思维的综合能力.难度大.
【解析】代入验证,当 1n 时,
( ) ( ) ( )f x ax x a x x x g
,则 ( ) ( )f x a x x ,
由 ( ) ( )f x a x x 可知, 1 2
1 , 13x x ,结合图像可知函数应在 10, 3
递增,在 1 ,13
递减,
即在 1
3x 取得最大值,由 ( ) ( )f a g ,知 a 存在.故选 A.
5.(北京理 6)根据统计,一名工人组装第 x 件某产品所用的时间(单位:分钟)为
,
( )
,
c x A
xf x c x A
A
(A,
c 为常数)。已知工人组装第 4 件产品用时 30 分钟,组装第 A 件
产品时用时 15 分钟,那么 c 和 A 的值分别是
A. 75,25 B. 75,16 C. 60,25 D. 60,16
【答案】D
【解析】由条件可知, x A 时所用时间为常数,所以组装第 4 件产品用时必然满足第一个分段函数,即
(4) 30 60
4
cf c , 60( ) 15 16f A A
A
,选 D。
6.(北京文 8)已知点 0,2A , 2,0B ,若点C 在函数 2y x 的图象上,则使得 ABC 的面积为 2 的点C
的个数为
A. 4 B. 3 C. 2 D. 1
【答案】A
7.(福建理 5) 1( 2 )0
xe x dx 等于
A.1 B. 1e C. e D. 1e
【答案】C
8.(福建理 9)对于函数 ( ) sinf x a x bx c (其中, , ,a b R c Z ),选取 , ,a b c 的一组值计算 (1)f 和
0.5 1
x
y
O
0.5
( 1)f ,所得出的正确结果一定不可能是
A.4 和 6 B.3 和 1 C.2 和 4 D.1 和 2
【答案】D
9.(福建理 10)已知函数 ( ) xf x e x ,对于曲线 ( )y f x 上横坐标成等差数列的三个点 A,B,C,给
出以下判断:
①△ABC 一定是钝角三角形
②△ABC 可能是直角三角形
③△ABC 可能是等腰三角形
④△ABC 不可能是等腰三角形
其中,正确的判断是
A.①③ B.①④ C.②③ D.②④
【答案】B
10.(福建文 6)若关于 x 的方程 x2+mx+1=0 有两个不相等的实数根,则实数 m 的取值范围是
A.(-1,1) B.(-2,2)
C.(-∞,-2)∪(2,+∞) D.(-∞,-1)∪(1,+∞)
【答案】C
11.(福建文 8)已知函数 f(x)=
2x, x>0
x+1,x≤0 ,若 f(a)+f(1)=0,则实数 a 的值等于
A.-3 B.-1 C.1 D.3
【答案】A
12.(福建文 10)若 a>0,b>0,且函数 f(x)=4x3-ax2-2bx+2 在 x=1 处有极值,则 ab 的最大值等于
A.2 B.3 C.6 D.9
【答案】D
13.(广东理 4)设函数 ( )f x 和 g(x)分别是 R 上的偶函数和奇函数,则下列结论恒成立的是
A. ( )f x +|g(x)|是偶函数 B. ( )f x -|g(x)|是奇函数
C.| ( )f x | +g(x)是偶函数 D.| ( )f x |- g(x)是奇函数
【答案】A
【解析】因为 g(x)是 R 上的奇函数,所以|g(x)|是 R 上的偶函数,从而 ( )f x +|g(x)|是偶函数,故选 A.
14.(广东文 4)函数 1( ) lg( 1)1f x xx
的定义域是 ( )
A. ( , 1) B. (1, ) C. ( 1,1) (1, ) D. ( , )
【答案】C
15.(广东文 10)设 )(),(),( xhxgxf 是 R 上的任意实值函数.如下定义两个函数 xgf 和 xgf ;
对任意 Rx , )(xgfxgf ; )(xgxfxgf .则下列等式恒成立的是( )
A. )(xhghfxhgf
B. )(xhghfxhgf
C. )(xhghfxhgf
D. )(xhghfxhgf
【答案】B
16.(湖北理 6)已知定义在 R 上的奇函数 xf 和偶函数 xg 满足
2 xx aaxgxf
1,0 aa 且 ,若 ag 2 ,则 2f
A. 2 B.
4
15 C.
4
17 D. 2a
【答案】B
【解析】由条件 222 22 aagf , 222 22 aagf ,即
222 22 aagf ,由此解得 22 g , 222 aaf ,
所以 2a ,
4
15222 22 f ,所以选 B.
17.(湖北理 10)放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象
成为衰变,假设在放射性同位素铯 137 的衰变过程中,其含量 M (单位:太贝克)与时间t (单位:年)
满足函数关系: 30
0 2
t
MtM
,其中 0M 为 0t 时铯 137 的含量,已知 30t 时,铯 137 的含量的变
化率是 2ln10 (太贝克/年),则 60M
A. 5 太贝克 B. 2ln75 太贝克 C. 2ln150 太贝克 D. 150 太贝克
【答案】D
【解析】因为 30
0
/ 22ln30
1 t
MtM
,则 2ln1022ln30
130 30
30
0
/
MM ,解得 6000 M ,
所以 302600
t
tM
,那么
1504
1600260060 30
60
M (太贝克),所以选 D.
18.(湖南文 7)曲线 sin 1
sin cos 2
xy x x
在点 ( ,0)4M 处的切线的斜率为( )
A. 1
2
B. 1
2 C. 2
2
D. 2
2
【答案】B
【解析】 2 2
cos (sin cos ) sin (cos sin ) 1' (sin cos ) (sin cos )
x x x x x xy x x x x
,所以
24
1 1'| 2(sin cos )4 4
x
y
。
19.(湖南文 8)已知函数 2( ) 1, ( ) 4 3,xf x e g x x x 若有 ( ) ( ),f a g b 则b 的取值范围为
A.[2 2,2 2] B. (2 2,2 2) C.[1,3] D. (1,3)
【答案】B
【解析】由题可知 ( ) 1 1xf x e , 2 2( ) 4 3 ( 2) 1 1g x x x x ,若有 ( ) ( ),f a g b 则
( ) ( 1,1]g b ,即 2 4 3 1b b ,解得 2 2 2 2b 。
20.(湖南理 6)由直线 , , 03 3x x y 与曲线 cosy x 所围成的封闭图形的面积为( )
A. 1
2 B.1 C. 3
2
D. 3
【答案】D
【解析】由定积分知识可得
3
3
3
3
3 3cos sin | ( ) 32 2S xdx x
,故选 D。
21.(湖南理 8)设直线 x t 与函数 2( ) , ( ) lnf x x g x x 的图像分别交于点 ,M N ,则当| |MN 达到最小
时t 的值为( )
A.1 B. 1
2 C. 5
2
D. 2
2
【答案】D
【解析】由题 2| | lnMN x x , ( 0)x 不妨令 2( ) lnh x x x ,则 1'( ) 2h x x x
,令 '( ) 0h x 解得
2
2x ,因 2(0, )2x 时, '( ) 0h x ,当 2( , )2x 时, '( ) 0h x ,所以当 2
2x 时,| |MN 达
到最小。即 2
2t 。
22.(江西文 3)若
1
2
1( ) log (2 1)f x x
,则 ( )f x 的定义域为( )
1( ,0)2
B. 1( , )2
C. 1( ,0) (0, )2
D. 1( ,2)2
【答案】C
【解析】
,00,2
1
112,012,012log
2
1
x
xxx
23.(江西文 4)曲线 xy e 在点 A(0,1)处的切线斜率为( )
A.1 B.2 C. e D. 1
e
【答案】A
【解析】 1,0, 0' exey x
24.(江西文 6)观察下列各式:则 2 3 47 49,7 343,7 2401 ,…,则 20117 的末两位数字为( )
A.01 B.43 C.07 D.49
【答案】B
【解析】
343***2011,200922011
168075,24014,3433,492,7
f
ffffxf x
25.(江西理 3)若 )12(log
1)(
2
1
x
xf ,则 )(xf 定义域为
A. )0,2
1( B. ]0,2
1( C. ),2
1( D. ),0(
【答案】A
【解析】由
0)12(log
012
2
1 x
x
解得
0
2
1
x
x ,故 02
1 x ,选 A
26.(江西理 4)设 xxxxf ln42)( 2 ,则 0)(' xf 的解集为
A. ),0( B. ),2()0,1( C. ),2( D. )0,1(
【答案】C
【解析】 )(xf 定义域为 ),0( ,又由 0)1)(2(2422)('
x
xx
xxxf ,解得 01 x 或
2x ,所以 0)(' xf 的解集 ),2(
27.(江西理 7)观察下列各式: 312555 , 1562556 , 7812557 ,…,则 20115 的末四位数字为
A. 3125 B. 5625 C. 0625 D.8125
【答案】D
【解析】观察可知当指数为奇数时,末三位为 125;又 )11004(252011 ,即 20115 为第 1004 个指数
为奇数的项,应该与第二个指数为奇数的项( 7812557 )末四位相同,∴ 20115 的末四位数字为 8125
28.(辽宁理 9)设函数
1,log1
1,2)(
2
1
xx
xxf
x
,则满足 2)( xf 的 x 的取值范围是
A. 1[ ,2] B.[0,2] C.[1,+ ] D.[0,+ ]
【答案】D
29.(辽宁理 11)函数 )(xf 的定义域为 R , 2)1( f ,对任意 Rx , 2)( xf ,则 42)( xxf 的解集
为
A.( 1 ,1) B.( 1 ,+ ) C.( , 1 ) D.( ,+ )
【答案】B
30.(辽宁文 6)若函数 ))(12()( axx
xxf 为奇函数,则 a=
A.
2
1 B.
3
2 C.
4
3 D.1
【答案】A
31.(全国Ⅰ理 2)下列函数中,既是偶函数又在 +(0, )单调递增的函数是
(A) 3y x (B) 1y x (C) 2 1y x (D) 2 xy
【答案】B
32.(全国Ⅰ理 9)由曲线 y x ,直线 2y x 及 y 轴所围成的图形的面积为
(A)10
3
(B)4 (C)16
3
(D)6
【答案】C
33. (全国Ⅰ理 12)函数 1
1y x
的图像与函数 2sin ( 2 4)y x x 的图像所有交点的横坐标之和等于
(A)2 (B) 4 (C) 6 (D)8
【答案】D
34.(全国Ⅰ文 4)曲线 2y 2 1x x 在点(1,0)处的切线方程为
(A) 1y x (B) 1y x
(C) 2 2y x (D) 2 2y x
【答案】A
35. (全国Ⅰ文 9)设偶函数 f(x)满足 f(x)=2x-4 (x 0),则 2 0x f x =
(A) 2 4x x x 或 (B) 0 4 x x x 或
(C) 0 6 x x x 或 (D) 2 2 x x x 或
【答案】B
36.(全国Ⅱ理 2)函数 y = 2 x ( x ≥0)的反函数为
(A) y =
2
4
x ( x ∈R) (B) y =
2
4
x ( x ≥0) (C) y = 24x ( x ∈R) (D) y = 24x ( x ≥0)
【答案】B
【命题意图】:本小题主要考查函数与反函数概念及求法特别要注意反函数的定义域即原函数的值域。
【解析】由 y = 2 x ,得 x =
2
4
y .函数 y = 2 x ( x ≥0)的反函数为 y =
2
4
x .( x ≥0)
37.(全国Ⅱ理 8)曲线 2 1xy e 在点(0,2)处的切线与直线 0y 和 y x 围成的三角形的面积为
(A) 1
3 (B) 1
2 (C) 2
3 (D)1
【答案】A
【命题意图】:本小题主要考查导数的求法、导数的几何意义及过曲线上一点切线的方程的求法。
【解析】 2
0 0| ( 2 ) | 2x
x xy e
,故曲线 2 1xy e 在点(0,2)处的切线方程为 2 2y x ,易得切
线与直线 0y 和 y x 围成的三角形的面积为 1
3
。
38.(全国Ⅱ理 9)设 ( )f x 是周期为 2 的奇函数,当 0 1x 时, ( ) 2 (1 )f x x x ,则 5( )2f
(A) 1
2
(B) 1
4
(C) 1
4 (D) 1
2
【答案】A
【命题意图】:本小题主要考查了函数的奇偶性、周期性的概念。
【解析】 5 5 1 1 1 1 1( ) ( 2) ( ) ( ) 2 (1 )2 2 2 2 2 2 2f f f f 。
39.(山东理 9)函数 2sin2
xy x 的图象大致是
【答案】C
【 解 析 】 因 为 ' 1 2cos2y x , 所 以 令 ' 1 2cos 02y x , 得 1cos 4x , 此 时 原 函 数 是 增 函 数 ; 令
' 1 2cos 02y x ,得 1cos 4x ,此时原函数是减函数,结合余弦函数图象,可得选 C 正确.
40.(山东理 10)已知 ( )f x 是 R 上最小正周期为 2 的周期函数,且当 0 2x 时, 3( )f x x x ,则函数
( )y f x 的图象在区间[0,6]上与 x 轴的交点的个数为
(A)6 (B)7 (C)8 (D)9
【答案】A
【解析】因为当 0 2x 时, 3( )f x x x ,又因为 ( )f x 是 R 上最小正周期为 2 的周期函数,且 (0) 0f ,
所以 (6) (4) (2) (0) 0f f f f ,又因为 (1) 0f ,所以 (3) 0f , (5) 0f ,故函数 ( )y f x 的图象
在区间[0,6]上与 x 轴的交点的个数为 6 个,选 A.
41.(山东文 4)曲线 3 11y x 在点 P(1,12)处的切线与 y 轴交点的纵坐标是
(A)-9 (B)-3 (C)9 (D)15
【答案】C
42.(陕西理 3)设函数 ( )f x ( xR)满足 ( ) ( )f x f x , ( 2) ( )f x f x ,则函数 ( )y f x 的图像
是 ( )
【答案】B
【分析】根据题意,确定函数 ( )y f x 的性质,再判断哪一个图像具有这些性质.
【解析】选由 ( ) ( )f x f x 得 ( )y f x 是偶函数,所以函数 ( )y f x 的图象关于 y 轴对称,可知 B,D
符合;由 ( 2) ( )f x f x 得 ( )y f x 是周期为 2 的周期函数,选项 D 的图像的最小正周期是 4,不符合,
选项 B 的图像的最小正周期是 2,符合,故选 B.
43.(陕西文 4) 函数 1
3y x 的图像是 ( )
【答案】B
【分析】已知函数解析式和图像,可以用取点验证的方法判断.
【解析】 取 1
8x , 1
8
,则 1
2y , 1
2
,选项 B,D 符合;取 1x ,则 1y ,选项 B 符合题意.
44.(上海理 16)下列函数中,既是偶函数,又是在区间 (0, ) 上单调递减的函数是( )
(A) 1ln | |y x
. (B) 3y x . (C) | |2 xy . (D) cosy x .
【答案】A
45.(上海文 15)下列函数中,既是偶函数,又在区间 (0, ) 上单调递减的函数是( )
(A) 2y x (B) 1y x (C) 2y x (D) 1
3y x
【答案】A
46.(四川理 7)若 ( )f x 是 R 上的奇函数,且当 0x 时, 1( ) ( ) 12
xf x ,则 ( )f x 的反函数的图象大致是
【答案】A
【解析】当 0x 时,函数 ( )f x 单调递减,值域为 (1,2) ,此时,其反函数单调递减且图象在 1x 与 2x 之
间,故选 A.
47.(四川文 4)函数 1( ) 12
xy 的图象关于直线 y=x 对称的图象像大致是
【答案】A
【解析】 1( ) 12
xy 图象过点 (0,2) ,且单调递减,故它关于直线 y=x 对称的图象过点 (2,0) 且单调递减,
选 A.
48.(天津理 2)函数 2 3xf x x 的零点所在的一个区间是( ).
A. 2, 1 B. 1,0 C. 0,1 D. 1,2
【答案】B
【解析】解法 1.因为 22 2 6 0f , 11 2 3 0f , 00 2 0 0f ,
所以函数 2 3xf x x 的零点所在的一个区间是 1,0 .故选B.
解法 2. 2 3 0xf x x 可化为 2 3x x .
画出函数 2xy 和 3y x 的图象,可观察出选项C,D不正确,且
00 2 0 0f ,由此可排除A,故选B.
49.(天津理 8)设函数
2
1
2
log , 0
log , 0
x x
f x x x
若 f a f a ,则实数 a 的取值范围是( ).
A. 1 0 0 1, ,U B. 1 1, , U
C. 1 0 1, , U D. 1 0 1, , U
【答案】C
【解析】若 0a ,则 2 1
2
log loga a ,即 22log 0a ,所以 1a ,
若 0a 则 1 2
2
log loga a ,即 22log 0a ,所以 0 1a , 1 0a 。
所以实数 a 的取值范围是 1a 或 1 0a ,即 1 0 1a , , U .故选 C.
50.(天津文 4)函数 e 2xf x x 的零点所在的一个区间是( ).
A. 2, 1 B. 1,0 C. 0,1 D. 1,2
【答案】C
【解析】因为 11 e 1 2 0f , 00 e 0 2 1 0f ,
11 e 1 2 e 1 0f ,所以函数 e 2xf x x 的零点所在的一个区间是 0,1 .故选C.
51.(天津文 6)设 5log 4a , 2
5log 3b , 4log 5c ,则( ).
A. a c b B.b c a
C. a b c D.b a c
【答案】D
【解析】因为 4 4log 5 log 4 1c c , 50 log 4 1a , 50 log 3 1a ,
所以 2
5 5 5 5log 3 log 3 log 4 log 4b a ,
所以 b a c ,故选D.
52.(天津文 10)设函数 2 2g x x xR ,
4, ,
, ,
g x x x g xf x g x x x g x
则 f x 的值域是
( ).
A. 9 ,0 1,4
U B. 0, ,
C. 9 ,4
D. 9 ,0 2,4
U
【答案】D
【解析】解 2 2x g x x 得 2 2 0x x ,则 1x 或 2x .因此 2 2x g x x 的解为:
1 2x .于是
2
2
2, 1 2,
2, 1 2,
x x x xf x
x x x
或
当 1x 或 2x 时, 2f x .
当 1 2x 时,
2
2 1 92 2 4x x x
,则 9
4f x ,
又当 1x 和 2x 时, 2 2 0x x ,所以 9 04 f x .
由以上,可得 2f x 或 9 04 f x ,因此 f x 的值域是 9 ,0 2,4
U .故选D.
53.(浙江理 1)已知
0),1(
02
xxf
xxxf ,则 22 ff 的值为
A.6 B.5 C.4 D.2
【答案】B
54.(浙江文 10)设函数 2 , ,f x ax bx c a b c R ,若 1x 为函数 2f x e 的一个极值点,则下
列图象不可能为 y f x 的图象是
【答案】D
55.(重庆理 5)下列区间中,函数 ( )f x = ln(2 )x 在其上为增函数的是
(A)(- ,1 ] (B) 41, 3
(C) 30, 2
(D) 1,2
【答案】D
56.(重庆理 10)设 m,k 为整数,方程 2 2 0mx kx 在区间(0,1)内有两个不同的根,则 m+k 的最小
值为
(A)-8 (B)8 (C)12 (D) 13
【答案】D
57. (重庆文 3)曲线 在点 , 处的切线方程为 A
(A) (B)
(C) (D)
58. (重庆文 6)设 , , ,则 , , 的大小关系是
(A) (B)
(C) (D)
【答案】B
59. (重庆文 7)若函数 在 处取最小值,则
(A) (B)
(C)3 (D)4
【答案】C
二、填空题
60. (重庆文 15)若实数 , , 满足 , ,则 的最大值是 .
【答案】 22 log 3
61.(浙江文 11)设函数 k 4( ) 1f x x
,若 ( ) 2f a ,则实数 a =________________________
【答案】-1
62.(天津文 16)设函数 1f x x x
.对任意 1,x , 0f mx mf x 恒成立,则实数 m 的取
值范围是 .
【答案】 , 1 .
【解析】解法 1.显然 0m ,由于函数 1f x x x
对 1,x 是增函数,
则当 0m 时, 0f mx mf x 不恒成立,因此 0m .
当 0m 时,函数 h x f mx mf x 在 1,x 是减函数,
因此当 1x 时, h x 取得最大值 11h m m
,
于是 0h x f mx mf x 恒成立等价于 h x 1,x 的最大值 0 ,
即 11 0h m m
,解
1 0,
0,
m m
m
得 1m .于是实数 m 的取值范围是 , 1 .
解法 2.然 0m ,由于函数 1f x x x
对 1,x 是增函数,则当 0m 时, 0f mx mf x
不成立,因此 0m .
2 2 2 21 1 2 12 0m m m x mf mx mf x mx mx mxmx x mx mx
,
因为 1,x , 0m ,则 2 2 22 1 0m x m ,设函数 2 2 22 1g x m x m ,则当 1,x 时为
增函数,于是 1x 时, g x 取得最小值 21 1g m .
解 21 1 0,
0,
g m
m
得 1m .于是实数 m 的取值范围是 , 1 .
解法 3.因为对任意 1,x , 0f mx mf x 恒成立,所以对 1x ,不等式 0f mx mf x
也成立,于是 1 0f m mf ,即 1 0m m
,解
1 0,
0,
m m
m
得 1m .于是实数 m 的取值范围是
, 1 .
63.(天津理 16)设函数 2 1f x x .对任意 3 ,2x
,
24 1 4xf m f x f x f mm
恒成立,则实数 m 的取值范围是 .
【答案】 3 3, ,2 2
U .
【解析】解法1.不等式化为 21 4 4 0xf x f m f m f xm
,即
2
2 2 2 2 2
21 1 4 4 1 4 4 0xx m m x mm
,
整理得 2 2
2
11 4 2 3 0m x xm
,
因为 2 0x ,所以 2
2 2
1 2 31 4 xmm x
,设 2
2 3xg x x
, 3 ,2x
.
于是题目化为 2
2
11 4m g xm
,对任意 3 ,2x
恒成立的问题.
为此需求 2
2 3xg x x
, 3 ,2x
的最大值.设 1u x
,则 20 3u .
函数 23 2g x h u u u 在区间 20, 3
上是增函数,因而在 2
3u 处取得最大值.
2 4 2 2 833 9 3 3h
,所以 2
max2
1 81 4 3m u xm
,
整理得 4 212 5 3 0m m ,即 2 24 3 3 1 0m m ,
所以 24 3 0m ,解得 3
2m 或 3
2m ,
因此实数 m 的取值范围是 3 3, ,2 2m
U .
解法 2.同解法 1,题目化为 2
2
11 4m g xm
,对任意 3 ,2x
恒成立的问题.
为此需求 2
2 3xg x x
, 3 ,2x
的最大值.
设 2 3t x ,则 6,t . 2
4 4
96 9 6
tg x h t t t t t
.
因为函数 9t t
在 3, 上是增函数,所以当 6t 时, 9t t
取得最小值 36 2
.
从而 h t 有最大值
4 8
3 36 62
.所以 2
max2
1 81 4 3m g xm
,整理得 4 212 5 3 0m m ,
即 2 24 3 3 1 0m m ,所以 24 3 0m ,解得 3
2m 或 3
2m ,
因此实数 m 的取值范围是 3 3, ,2 2m
U .
解法 3.不等式化为 21 4 4 0xf x f m f m f xm
,即
2
2 2 2 2 2
21 1 4 4 1 4 4 0xx m m x mm
,
整理得 2 2
2
11 4 2 3 0m x xm
,
令 2 2
2
1( ) 1 4 2 3F x m x xm
.
由于 0 3 0F ,则其判别式 0 ,因此 F x 的最小值不可能在函数图象的顶点得到,
所以为使 ( ) 0F x 对任意 3 ,2x
恒成立,必须使 3
2F
为最小值,
即实数 m 应满足
2
2
2
2
11 4 0;
3 0;2
2 3
1 22 1 4
mm
F
mm
解得 2 3
4m ,因此实数 m 的取值范围是 3 3, ,2 2m
U .
解法 4.(针对填空题或选择题)由题设,因为对任意 3 ,2x
,
24 1 4xf m f x f x f mm
恒成立,
则对 3
2x ,不等式 24 1 4xf m f x f x f mm
也成立,
把 3
2x 代入上式得 23 3 14 42 2 2f m f f f mm
,即
2 2 2
2
9 9 11 4 4 1 4 44 44
m m m
m
,因为 24 0m ,上式两边同乘以 24m ,并整理得
4 212 5 3 0m m ,即 2 24 3 3 1 0m m ,所以 24 3 0m ,解得 3
2m 或 3
2m ,
因此实数 m 的取值范围是 3 3, ,2 2m
U .
64.(四川理 13)计算
1
21(lg lg25) 100 =4
_______.
【答案】-20
【解析】
1
2
1
2
1 lg2 lg5 1(lg lg25) 100 2 2 lg10 204 10100
.
65.(四川理 16)函数 ( )f x 的定义域为 A,若 1 2,x x A 且 1 2( ) ( )f x f x 时总有 1 2x x ,则称 ( )f x 为单函数.例
如,函数 ( )f x =2x+1( xR )是单函数.下列命题:
①函数 2( )f x x (xR)是单函数;
②若 ( )f x 为单函数, 1 2,x x A 且 1 2x x ,则 1 2( ) ( )f x f x ;
③若 f:A→B 为单函数,则对于任意 b B ,它至多有一个原象;
④函数 ( )f x 在某区间上具有单调性,则 ( )f x 一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
【答案】②③
【解析】对于①,若 1 2( ) ( )f x f x ,则 1 2x x ,不满足;②实际上是单函数命题的逆否命题,故为真命题;
对于③,若任意 b B ,若有两个及以上的原象,也即当 1 2( ) ( )f x f x 时,不一定有 1 2x x ,不满足题设,
故该命题为真;根据定义,命题④不满足条件.
66.(上海文 3)若函数 ( ) 2 1f x x 的反函数为 1( )f x ,则 1( 2)f
【答案】 3
2
67.(上海文 12)行列式 ( , , , { 1,1,2}a b a b c dc d
所有可能的值中,最大的是
【答案】 15
2
68.(上海文 14)设 ( )g x 是定义在 R 上,以 1 为周期的函数,若函数 ( ) ( )f x x g x 在区间[0,1] 上的值
域为[ 2,5] ,则 ( )f x 在区间[0,3]上的值域为
【答案】[ 2,7]
69.(上海理 1)函数 1( ) 2f x x
的反函数为 1( )f x .
【答案】 1 2x
70.(上海理 10)行列式 ( , , , { 1,1,2})a b a b c dc d
所有可能的值中,最大的是 .
【答案】 6
71.(上海理 13) 设 ( )g x 是定义在 R 上,以 1 为周期的函数,若函数 ( ) ( )f x x g x 在区间[3,4]上的
值域为[ 2,5] ,则 ( )f x 在区间[ 10,10] 上的值域为 .
【答案】[ 15,11]
72.(陕西文 11)设 lg , 0
( )
10 , 0x
x x
f x
x
,则 ( ( 2))f f ______.
【答案】 2
【分析】由 2x 算起,先判断 x 的范围,是大于 0,还是不大于 0,;再判断 ( 2)f 作为自变量的值时的
范围,最后即可计算出结果.
【解析】∵ 2 0x ,∴ 2 1( 2) 10 0100f ,所以 2 2(10 ) lg10 2f ,即 ( ( 2)) 2f f .
73.(陕西理 11)设 2
0
lg 0
( )
3 0
a
x x
f x
x t dt x
,若 ( (1)) 1f f ,则 a .
【分析】分段函数问题通常需要分布进行计算或判断,从 1x 算起是解答本题的突破口.
【解析】因为 1 0x ,所以 (1) lg1 0f ,又因为 2 3
0
( ) 3
a
f x x t dt x a ,
所以 3(0)f a ,所以 3 1a , 1a .
【答案】1
74.(陕西理 12)设 n N ,一元二次方程 2 4 0x x n 有整数根的充要条件是 n .
【答案】3 或 4
【分析】直接利用求根公式进行计算,然后用完全平方数、整除等进行判断计算.
【解析】 4 16 4
2
nx 2 4 n ,因为 x 是整数,即 2 4 n 为整数,所以 4 n 为整数,且
4n ,又因为 n N ,取 1,2,3,4n ,验证可知 3,4n 符合题意;反之 3,4n 时,可推出一元二次方
程 2 4 0x x n 有整数根.
75.(山东理 16)已知函数 f x( )= log ( 0 a 1).a x x b a > ,且 当 2<a<3<b<4 时,函数 f x( )的零
点 *
0 ( , 1), , n=x n n n N 则 .
【答案】5
【解析】方程 log ( 0 a 1)a x x b a > ,且 =0 的根为 0
x ,即函数 log (2 3)ay x a 的图象与函数
(3 4)y x b b 的交点横坐标为 0
x ,且 *
0 ( , 1),x n n n N ,结合图象,因为当 (2 3)x a a
时 , 1y , 此 时 对 应 直 线 上 1y 的 点 的 横 坐 标 1 (4,5)x b ; 当 2y 时 , 对 数 函 数
log (2 3)ay x a 的图象上点的横坐标 (4,9)x ,直线 (3 4)y x b b 的图象上点的横坐标
(5,6)x ,故所求的 5n .
76.(辽宁文 16)已知函数 axexf x 2)( 有零点,则 a 的取值范围是___________.
【答案】 ( ,2ln 2 2]
77.(江苏 2)函数 )12(log)( 5 xxf 的单调增区间是__________
【答案】 +1(- , )2
【解析】 5logy u 在 (0, ) . 2 1u x 在 1( , ),2x 大于零,且增.
本题主要考查函数的概念,基本性质,指数与对数,对数函数图象和性质,容易题
78.(江苏 8)在平面直角坐标系 xOy 中,过坐标原点的一条直线与函数
xxf 2)( 的图象交于 P、Q 两点,
则线段 PQ 长的最小值是________.
【答案】4.
【解析】设经过原点的直线与函数的交点为 2( , )x x
, 2( , )x x
,则 2 24(2 ) ( ) 4PQ x x
.
本题主要考查幂函数,函数图象与性质,函数与方程,函数模型及其应用,两点间距离公式以及基本不等式,
中档题.
79.(江苏 11)已知实数 0a ,函数
1,2
1,2)( xax
xaxxf ,若 )1()1( afaf ,则 a 的值为________
【答案】 3
4a
【解析】 0a .
30,2 2 1 2 , 2a a a a a a ,不符合;
30, 1 2 2 2 , 4a a a a a a .
本题主要考查函数概念,函数与方程,函数模型及其应用,含参的分类讨论,中档题.
80.(江苏 12)在平面直角坐标系 xOy 中,已知点 P 是函数 )0()( xexf x 的图象上的动点,该图象在
P 处的切线l 交 y 轴于点 M,过点 P 作l 的垂线交 y 轴于点 N,设线段 MN 的中点的纵坐标为 t,则 t 的最
大值是_____________
【答案】 1 1( )2 e e
【解析】设 0
0( , ),xP x e 则 0 0 0
0 0: ( ), (0,(1 ) )x x xl y e e x x M x e ,过点 P 作l 的垂线
0 0 0 0
0 0( ), (0, )x x x xy e e x x N e x e ,
0 0 0 0 0 0
0 0 0
1 1[(1 ) ] ( )2 2
x x x x x xt x e e x e e x e e
0 0
0
1 ( )(1 )2
x xt e e x ,所以,t 在 (0,1) 上单调增,在 (1, ) 单调减,
0 max
1 11, ( )2x t e e
.
本题主要考查指数运算,指数函数图象、导数的概念,导数公式,导数的运算与几何意义、利用导数研究函数,
导数的应用、直线方程及其斜率、直线的位置关系,运算求解能力,综合应用有关知识的能力,本题属难题.
81.(湖南文 12)已知 ( )f x 为奇函数, ( ) ( ) 9, ( 2) 3, (2)g x f x g f 则 .
【答案】6
【解析】 ( 2) ( 2) 9 3, ( 2) 6g f f 则 ,又 ( )f x 为奇函数,所以
(2) ( 2) 6f f 。
82.(湖北文 15)里氏震级 M 的计算公式为: 0lg lgM A A ,其中 A 是测震仪记录的地震曲线的最大
振幅
是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是 1000,此时标准地震的振幅为
0.001,则此次地震的震级为__________级;9 级地震的最大的振幅是 5 级地震最大振幅的__________倍。
【答案】6,10000
83.(广东文 12)设函数 .1cos)( 3 xxxf 若 11)( af ,则 )( af .
【答案】-9
84.(广东理 12)函数 3 2( ) 3 1f x x x 在 x 处取得极小值.
【答案】
.2)(
),2,0(),,2(),0,(:)(),2(363x(x)': 2
处取得极小值在
递减区间为的单调递增区间为解析
xxf
xfxxxf
85.
(北京理 13)已知函数
3
2 , 2( )
( 1) , 2
xf x x
x x
,若关于 x 的方程 ( )f x k 有两个不同的
实根,则实数 k 的取值范围是________.
【答案】
【解析】 2( ) ( 2)f x xx
单调递减且值域为(0,1], 3( ) ( 1) ( 2)f x x x 单调递增且值域为 ( ,1) ,
( )f x k 有两个不同的实根,则实数 k 的取值范围是(0,1)。
86.(安徽文 13)函数 2
1
6
y
x x
的定义域是 .
【答案】(-3,2)【命题意图】本题考查函数的定义域,考查一元二次不等式的解法.
【解析】由 26 0x x 可得 2 6 0x x ,即 +3 2 0x x ,所以 3 2x .
三、解答题
87.(安徽理 16)设 ( ) 1
xef x ax
,其中 a 为正实数
(Ⅰ)当 a 4
3
时,求 ( )f x 的极值点;
(Ⅱ)若 ( )f x 为 R 上的单调函数,求 a 的取值范围。
本题考查导数的运算,极值点的判断,导数符号与函数单调变化之间的关系,求解二次不等式,考查运算
能力,综合运用知识分析和解决问题的能力.
解:对 )(xf 求导得 .
)1(
1)( 22
2
ax
axaxexf x
①
(I)当
3
4a ,若 .2
1,2
3,0384,0)( 21
2 xxxxxf 解得则
综合①,可知
所以,
2
3
1 x 是极小值点,
2
1
2 x 是极大值点.
x )2
1,(
2
1 )2
3,2
1( 2
3 ),2
3(
)(xf + 0 - 0 +
)(xf ↗ 极大值 ↘ 极小值 ↗
(II)若 )(xf 为 R 上的单调函数,则 )(xf 在 R 上不变号,结合①与条件 a>0,知 0122 axax
在 R 上恒成立,因此 ,0)1(444 2 aaaa 由此并结合 0a ,知 .10 a
88.(北京理 18)已知函数 k
x
ekxxf 2)()( .
(1)求 )(xf 的单调区间;
(2)若对 0(x , ) ,都有
exf 1)( ,求 k 的取值范围。
解:(1) / 2 21( ) ( )
x
kf x x k ek
,令 / ( ) 0f x 得 x k
当 0k 时, ( )f x 在 ( , )k 和 ( , )k 上递增,在 ( , )k k 上递减;
当 0k 时, ( )f x 在 ( , )k 和 ( , )k 上递减,在 ( , )k k 上递增
(2) 当 0k 时,
1 1( 1)
k
kf k e e
;所以不可能对 0(x , ) 都有
exf 1)( ;
当 0k 时有(1)知 ( )f x 在 (0, ) 上的最大值为
24( ) kf k e
,所以对 0(x , ) 都有
exf 1)(
即
24 1 1 02
k ke e
,故对 0(x , ) 都有
exf 1)( 时, k 的取值范围为 1[ ,0)2
。
89.(北京文 18)已知函数 xf x x k e ,(I)求 f x 的单调区间;
(II)求 f x 在区间 0,1 上的最小值。
解:(I) / ( ) ( 1) xf x x k e ,令 / ( ) 0 1f x x k ;所以 f x 在 ( , 1)k 上递减,在 ( 1, )k
上递增;
(II)当 1 0, 1k k 即 时,函数 f x 在区间 0,1 上递增,所以 min( ) (0)f x f k ;
当 0 1 1k 即1 2k 时,由(I)知,函数 f x 在区间 0, 1k 上递减, ( 1,1]k 上递增,所以
1
min( ) ( 1) kf x f k e ;
当 1 1, 2k k 即 时,函数 f x 在区间 0,1 上递减,所以 min( ) (1) (1 )f x f k e 。
90.(福建理 18)某商场销售某种商品的经验表明,该商品每日的销售量 y (单位:千克)与销售价格 x (单
位:元/千克)满足关系式 210( 6)3
ay xx
,其中3 6x ,a 为常数,已知销售价格为 5 元/千克时,
每日可售出该商品 11 千克.
(Ⅰ) 求 a 的值;
(Ⅱ) 若该商品的成品为 3 元/千克, 试确定销售价格 x 的值,使商场每日销售该商品所获得的利润最大.
解:(Ⅰ)因为 5x 时 11y ,所以 10 11 22
a a ;
(Ⅱ)由(Ⅰ)知该商品每日的销售量 22 10( 6)3y xx
,所以商场每日销售该商品所获得的利润:
2 22( ) ( 3)[ 10( 6) ] 2 10( 3)( 6) ,3 63f x x x x x xx
;
/ 2( ) 10[( 6) 2( 3)( 6)] 30( 4)( 6)f x x x x x x ,令 / ( ) 0f x 得 4x
函数 ( )f x 在 (3,4) 上递增,在 (4,6) 上递减,所以当 4x 时函数 ( )f x 取得最大值 (4) 42f
答:当销售价格 4x 时,商场每日销售该商品所获得的利润最大,最大值为 42.
91.(福建文 22)已知 a、b 为常数,且 a≠0,函数 f(x)=-ax+b+axlnx,f(e)=2,(e=2.71828…是自然对
数的底数)。
(Ⅰ)求实数 b 的值;
(Ⅱ)求函数 f(x)的单调区间;
(Ⅲ)当 a=1 时,是否同时存在实数 m 和 M(m<M),使得对每一个 t∈[m,M],直线 y=t 与曲线 y=
f(x)(x∈[1
e
,e])都有公共点?若存在,求出最小的实数 m 和最大的实数 M;若不存在,说明理由。
解:(Ⅰ)b=2;(Ⅱ)a>0 时单调递增区间是(1,+∞),单调递减区间是(0,1),a<0 时单调递增区
间是(0,1),单调递减区间是(1,+∞);(Ⅲ)存在 m,M;m 的最小值为 1,M 的最大值为 2。
92.(广东理 21)
2 2
1 2
2
1 2
2
0 0 0
0
1, L: . , 4 0, ,4
0 , ( , ) max{| |,| |}.
1(1) ( , )( 0) y B. : AB Q( , ),4
| |( , ) ;2
xOy y x p q p q x x
x px q p q x x
A p p p L p q
pp q
在平面直角坐标系 上 给定抛物线 实数 满足 是方程
的两根 记
过点 作 的切线交 轴于点 证明 对线段 上的作一点
有
(2)设 ( , )M a b 是定点,其中 ,a b 满足 2 4 0a b a >0, ≠ .过 ( , )M a b 作 L 的两条切线 1 2,l l ,切点分别为
2 2
1 1 2 2
1 1( , ), '( , )4 4E p p E P P , 1 2,l l 与 y 分别交于 , 'F F .线段 EF 上异于两端点的点集记为 X .证明:
1
1 2
| |( , ) ( , ) 2
PM a b X P P a b
2
min max
1 5( , ) 1, ( 1) , ,4 4
, ).
D x y y x y x p q
p q
(3)设 当点( )取遍D时,求
( )的最小值(记为 )和最大值(记为
;
解:(1)
0 0 0
1 1' | ( ) |2 2AB x p x pk y x p ,
直线 AB 的方程为 2
0 0 0
1 1 ( )4 2y p p x p ,即 2
0 0
1 1
2 4y p x p ,
2
0 0
1 1
2 4q p p p ,方程 2 0x px q 的判别式 2 2
04 ( )p q p p ,
两根 0 0
1,2
| |
2 2
p p p px 或 0
2
pp ,
0 0p p , 0 0| | || | | ||2 2
p pp p ,又 00 | | | |p p ,
0 0 0| | | | | | | |2 2 2
p p pp ,得 0 0 0| | || | | || | |2 2 2
p p pp p ,
0( , ) | |2
pp q .
(2)由 2 4 0a b 知点 ( , )M a b 在抛物线 L 的下方,
①当 0, 0a b 时,作图可知,若 ( , )M a b X ,则 1 2 0p p ,得 1 2| | | |p p ;
若 1 2| | | |p p ,显然有点 ( , )M a b X ; ( , )M a b X 1 2| | | |p p .
②当 0, 0a b 时,点 ( , )M a b 在第二象限,
作图可知,若 ( , )M a b X ,则 1 20p p ,且 1 2| | | |p p ;
若 1 2| | | |p p ,显然有点 ( , )M a b X ;
( , )M a b X 1 2| | | |p p .
根据曲线的对称性可知,当 0a 时, ( , )M a b X 1 2| | | |p p ,
综上所述, ( , )M a b X 1 2| | | |p p (*);
由(1)知点 M 在直线 EF 上,方程 2 0x ax b 的两根 1
1,2 2
px 或 1
2
pa ,
同理点 M 在直线 ' 'E F 上,方程 2 0x ax b 的两根 2
1,2 2
px 或 2
2
pa ,
若 1( , ) | |2
pa b ,则 1| |2
p 不比 1| |2
pa 、 2| |2
p 、 2| |2
pa 小,
1 2| | | |p p ,又 1 2| | | |p p ( , )M a b X ,
1( , ) | |2
pa b ( , )M a b X ;又由(1)知, ( , )M a b X 1( , ) | |2
pa b ;
1( , ) | |2
pa b ( , )M a b X ,综合(*)式,得证.
(3)联立 1y x , 21 5( 1)4 4y x 得交点 (0, 1), (2,1) ,可知 0 2p ,
过点 ( , )p q 作抛物线 L 的切线,设切点为 2
0 0
1( , )4x x ,则
2
0
0
0
1
14
2
x q
xx p
,
得 2
0 02 4 0x px q ,解得 2
0 4x p p q ,
又 21 5( 1)4 4q p ,即 2 4 4 2p q p ,
0 4 2x p p ,设 4 2 p t , 2
0
1 22x t t 21 5( 1)2 2t ,
0
max max| |2
x ,又 0
5
2x , max
5
4
;
1q p , 2
0 4 4 | 2 | 2x p p p p p ,
0
min min| | 12
x .
93.(广东文 19) 设 0a ,讨论函数 xaxaaxxf )1(2)1(ln)( 2 的单调性.
解:函数 f(x)的定义域为(0,+∞)
2
2
1 2
1 2 1 2
2 (1 ) 2(1 ) 1'( ) ,
11 2 (1 ) 2(1 ) 1 0 12( 1)( )3
1 0, '( ) 23
( 1)(3 1) ( 1)(3 1)1 10, ,2 2 (1 ) 2 2 (1 )
0 '( ) 0, ( ) (0, ) ( , )
a a x a xf x x
a a a x a x a a
a f x
a a a ax xa a a a a a
x x x x f x f x x x
当 时,方程 的判别式
①当0< 时, 有 个零点
且当 或 时, 在 与 内为增函数
1 2 1 2
1 2
'( ) 0, ( ) , )
1 1 0, '( ) 0, ( ) (0, )3
11 '( ) 0( 0), ( ) (0, )
( 1)(3 1) ( 1)(3 1)1 11 0, 0, 0, '( )2 2 (1 ) 2 2 (1 )
x x x f x f x x x
a f x f x
a f x x f xx
a a a aa x x f x xa a a a a a
;
当 时, 在( 内为减函数
当 时, 在 内为增函数;
当 时, 在 内为增函数;
当 时, 所以 在定义域内有唯一零点
�
�
� 1
1 1 1 1
;
0 '( ) 0, ( ) (0, ) '( ) 0, ( ) ( , )x x f x f x x x x f x f x x 且当 时, 在 内为增函数;当 时, 在 内为减函数;
综上所述,f(x)的单调区间如下表:
10 3a 1 13 a 1a
1(0, )x 1 2( , )x x 2( , )x (0, ) 1(0, )x 1( , )x
(其中 1 2
( 1)(3 1) ( 1)(3 1)1 1,2 2 (1 ) 2 2 (1 )
a a a ax xa a a a a a
)
94.(湖北理 17)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车
流速度 v (单位:千米/小时)是车流密度 x (单位:辆/千米)的函数.当桥上的车流密度达到 200 辆/千
米时,造成堵塞,此时车流速度为 0;当车流密度不超过 20 辆/千米时,车流速度为 60 千米/小时.研究表
明:当 20020 x 时,车流速度 v 是车流密度 x 的一次函数.
(Ⅰ)当 2000 x 时,求函数 xv 的表达式;
(Ⅱ)当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
xvxxf 可以达到最大,并求出最大值.(精确到 1 辆/小时)
本题主要考查函数、最值等基础知识,同时考查运用数学知识解决实际问题的能力.
解析:(Ⅰ)由题意:当 200 x 时, 60xv ;当 20020 x 时,设 baxxv ,显然 baxxv
在 200,20 是减函数,由已知得
6020
0200
ba
ba ,解得
3
200
3
1
b
a
故函数 xv 的表达式为 xv =
.20020,2003
1
,200,60
xx
x
(Ⅱ)依题意并由(Ⅰ)可得 xf
.20020,2003
1
,200,60
xxx
xx
当 200 x 时, xf 为增函数,故当 20x 时,其最大值为 12002060 ;
当 20020 x 时,
3
10000
2
200
3
12003
1 2
xxxxxf ,
当且仅当 xx 200 ,即 100x 时,等号成立.
所以,当 100x 时, xf 在区间 200,20 上取得最大值
3
10000 .
综上,当 100x 时, xf 在区间 200,0 上取得最大值 33333
10000 ,
即当车流密度为 100 辆/千米时,车流量可以达到最大,最大值约为 3333 辆/小时.
95.(湖北理 21)(Ⅰ)已知函数 ( ) ln 1f x x x , (0, )x ,求函数 ( )f x 的最大值;
(Ⅱ)设 ,k ka b ( 1,2k …, )n 均为正数,证明:
(1)若 1 1 2 2a b a b … n na b 1 2b b … nb ,则 1 2
1 2 1nbb b
na a a ;
(2)若 1 2b b … nb =1,则 1
n
1 2
1 2
nbb b
nb b b 2
1b 2
2b …+ 2
nb 。
解:(Ⅰ) ( )f x 的定义域为 (0, ) ,令 / 1( ) 1 0 1f x xx
,
( )f x 在 (0,1) 上递增,在 (1, ) 上递减,故函数 ( )f x 在 1x 处取得最大值 (1) 0f
(Ⅱ)(1)由(Ⅰ)知当 (0, )x 时有 ( ) (1) 0f x f 即 ln 1x x ,
∵ , 0k ka b ,∴
1 1
ln ( 1),( 1,2, ) ln ( 1)k
n n
b
k k k k k k k
k k
b a b a k n a b a
∵
1 1
n n
k k k
k k
a b b
∴
1
ln 0k
n
b
k
k
a
即 1 2 1 2
1 2 1 2ln( ) 0 1n nb bb b b b
n na a a a a a
(2)①先证 1 2
1 2
1nbb b
nb b b n
,令 1 ,( 1,2, , )k
k
a k nnb
,则
1
1 1
n
k k k k
k
a b a bn
由(1)知 1 21 2
1 2
1 2 1 2
1 1 1 1( ) ( ) ( ) 1n n
n
b b b bb b
bb b
n n
n nnb nb nb b b b
∴ 1 2
1 2
1nbb b
nb b b n
;
②再证 1 2
1 2
nbb b
nb b b 2
1b 2
2b …+ 2
nb ,记 2
1
, ,( 1,2, , )
n
k
k k
k
bS b a k nS
则 2
1 1 1
1 1
n n n
k k k k
k k k
a b b bS
于是由(1)得
1 21 2 1 21 2
1 2( ) ( ) ( ) 1n n nb b b b bb b b bn
n
b b b b b b S SS S S
所以 1 2
1 2
nbb b
nb b b 2
1b 2
2b …+ 2
nb 。综合①②,(2)得证
96.(湖北文 20)设函数 3 2( ) 2f x x ax bx a , 2( ) 3 2g x x x ,其中 x R ,a、b 为常数,已
知曲线 ( )y f x 与 ( )y g x 在点(2,0)处有相同的切线l 。
(I) 求 a、b 的值,并写出切线l 的方程;
(II)若方程 ( ) ( )f x g x mx 有三个互不相同的实根 0、 1x 、 2x ,其中 1 2x x ,且对任意的 1 2,x x x ,
( ) ( ) ( 1)f x g x m x 恒成立,求实数 m 的取值范围。
解:(I) / 2 /( ) 3 4 , ( ) 2 3f x x ax b g x x ,由于曲线曲线 ( )y f x 与 ( )y g x 在点(2,0)处有相同
的切线,故有 / /(2) (2) 0, (2) (2) 1f g f g ,由此解得: 2, 5a b ;
切线 l 的方程: 2 0x y ‘
(II)由(I)得 3 2( ) ( ) 3 2f x g x x x x ,依题意得:方程 2( 3 2 ) 0x x x m 有三个互不相等的根
1 20, ,x x ,故 1 2,x x 是方程 2 3 2 0x x m 的两个相异实根,所以
19 4(2 ) 0 4m m ;
又对任意的 1 2,x x x , ( ) ( ) ( 1)f x g x m x 恒成立,特别地,取 1x x 时,
1 1 1( ) ( )f x g x mx m 成立,即 0 0m m ,由韦达定理知: 1 2 1 23 0, 2 0x x x x m ,
故 1 20 x x ,对任意的 1 2,x x x ,有 2 10, 0, 0x x x x x ,则:
1 2( ) ( ) ( )( ) 0f x g x mx x x x x x ;又 1 1 1( ) ( ) 0f x g x mx
所以函数在 1 2,x x x 上的最大值为 0,于是当 0m 时对任意的 1 2,x x x , ( ) ( ) ( 1)f x g x m x 恒
成立;综上: m 的取值范围是 1( ,0)4
。
97.(湖南文 22)设函数 1( ) ln ( ).f x x a x a Rx
(I)讨论 ( )f x 的单调性;
(II)若 ( )f x 有两个极值点 1 2x x和 ,记过点 1 1 2 2( , ( )), ( , ( ))A x f x B x f x 的直线的斜率为 k ,问:是否存在
a ,使得 2 ?k a 若存在,求出 a 的值,若不存在,请说明理由.
解析:(I) ( )f x 的定义域为 (0, ).
2
2 2
1 1'( ) 1 a x axf x x x x
令 2( ) 1,g x x ax 其判别式 2 4.a
当| | 2 , 0, '( ) 0,a f x 时 故 ( ) (0, )f x 在 上单调递增.
当 2a 时, >0,g(x)=0 的两根都小于 0,在 (0, ) 上, '( ) 0f x ,故 ( ) (0, )f x 在 上单调递增.
当 2a 时, >0,g(x)=0 的两根为
2 2
1 2
4 4,2 2
a a a ax x ,
当 10 x x 时, '( ) 0f x ;当 1 2x x x 时, '( ) 0f x ;当 2x x 时, '( ) 0f x ,故 ( )f x 分别在
1 2(0, ),( , )x x 上单调递增,在 1 2( , )x x 上单调递减.
(II)由(I)知, 2a .
因为 1 2
1 2 1 2 1 2
1 2
( ) ( ) ( ) (ln ln )x xf x f x x x a x xx x
,所以
1 2 1 2
1 2 1 2 1 2
( ) ( ) ln ln11f x f x x xk ax x x x x x
又由(I)知, 1 2 1x x .于是 1 2
1 2
ln ln2 x xk a x x
若存在 a ,使得 2 .k a 则 1 2
1 2
ln ln 1x x
x x
.即 1 2 1 2ln lnx x x x .亦即
2 2 2
2
1 2ln 0( 1)(*)x x xx
再 由 ( I ) 知 , 函 数 1( ) 2lnh t t tt
在 (0, ) 上 单 调 递 增 , 而 2 1x , 所 以
2 2
2
1 12ln 1 2ln1 0.1x xx
这与 (*)式矛盾.故不存在 a ,使得 2 .k a
98.(湖南理 20)如图 6,长方形物体 E 在雨中沿面 P(面积为 S)的垂直方向作匀速移动,速度为 ( 0)v v ,
雨速沿 E 移动方向的分速度为 ( )c c R 。E 移动时单位时间内的淋雨量包括两部分:(1)P 或 P 的平行面
(只有一个面淋雨)的淋雨量,假设其值与 v c ×S 成正比,比例系数为 1
10
;(2)其它面的淋雨量之和,
其 值 为 1
2
, 记 y 为 E 移 动 过 程 中 的 总 淋 雨 量 , 当 移 动 距 离 d=100 , 面 积 S= 3
2
时 。
(Ⅰ)写出 y 的表达式
(Ⅱ)设 0<v≤10,0<c≤5,试根据 c 的不同取值范围,确定移动速度 v ,使总淋雨量 y 最少。
解析:(I)由题意知,E 移动时单位时间内的淋雨量为 3 1| |20 2v c ,
故 100 3 1 5( | | ) (3| | 10)20 2y v c v cv v
.
(II)由(I)知,当 0 v c 时, 5 5(3 10)(3 3 10) 15cy c vv v
;
当 10c v 时, 5 5(10 3 )(3 3 10) 15cy v cv v
.
故
5(3 10) 15,0
5(10 3 ) 15, 10
c v cvy c c vv
。
(1)当 100 3c 时, y 是关于 v 的减函数.故当 10v 时, min
320 2
cy 。
(2) 当10 53 c 时,在 (0, ]c 上,y 是关于 v 的减函数;在 ( ,10]c 上,y 是关于 v 的增函数;故当 v c 时,
min
50y c
。
99.(湖南理 22) 已知函数 f ( x ) = 3x ,g ( x )= x + x 。
(Ⅰ)求函数 h ( x )= f ( x )-g ( x )的零点个数,并说明理由;
(Ⅱ)设数列 *{ }( )na n N 满足 1 ( 0)a a a , 1( ) ( )n nf a g a ,证明:存在常数 M,使得对于任意的
*n N ,都有 na ≤ M .
解析:(I)由 3( )h x x x x 知, [0, )x ,而 (0) 0h ,且 (1) 1 0, (2) 6 2 0h h ,则 0x
为 ( )h x 的一个零点,且 ( )h x 在 1 2(,)内有零点,因此 ( )h x 至少有两个零点
解法 1:
1
2 21'( ) 3 1 2h x x x
,记
1
2 21( ) 3 1 2x x x
,则
3
21'( ) 6 4x x x
。
当 (0, )x 时, '( ) 0x ,因此 ( )x 在 (0, ) 上单调递增,则 ( )x 在 (0, ) 内至多只有一个零点。
又因为 3(1) 0, ( ) 03
,则 ( )x 在 3( ,1)3
内有零点,所以 ( )x 在 (0, ) 内有且只有一个零点。记
此零点为 1x ,则当 1(0, )x x 时, 1( ) '( ) 0x x ;当 1( , )x x 时, 1( ) '( ) 0x x ;
所以,
当 1(0, )x x 时, ( )h x 单调递减,而 (0) 0h ,则 ( )h x 在 1(0, ]x 内无零点;
当 1( , )x x 时, ( )h x 单调递增,则 ( )h x 在 1( , )x 内至多只有一个零点;
从而 ( )h x 在 (0, ) 内至多只有一个零点。综上所述, ( )h x 有且只有两个零点。
解法 2: 1
2 2( ) ( 1 )h x x x x
,记 1
2 2( ) 1x x x
,则
3
21'( ) 2 2x x x
。
当 (0, )x 时, '( ) 0x ,因此 ( )x 在 (0, ) 上单调递增,则 ( )x 在 (0, ) 内至多只有一个零点。
因此 ( )h x 在 (0, ) 内也至多只有一个零点,
综上所述, ( )h x 有且只有两个零点。
(II)记 ( )h x 的正零点为 0x ,即 3
0 0 0x x x 。
(1)当 0a x 时,由 1a a ,即 1 0a x .而 3 3
2 1 1 0 0 0a a a x x x ,因此 2 0a x ,由此猜测:
0na x 。下面用数学归纳法证明:
①当 1n 时, 1 0a x 显然成立;
②假设当 ( 1)n k k 时,有 0ka x 成立,则当 1n k 时,由
3 3
1 0 0 0k k ka a a x x x 知, 1 0ka x ,因此,当 1n k 时, 1 0ka x 成立。
故对任意的 *n N , 0na x 成立。
(2)当 0a x 时,由(1)知, ( )h x 在 0( , )x 上单调递增。则 0( ) ( ) 0h a h x ,即 3a a a 。从而
3 3
2 1 1a a a a a a ,即 2a a ,由此猜测: na a 。下面用数学归纳法证明:
①当 1n 时, 1a a 显然成立;
②假设当 ( 1)n k k 时,有 ka a 成立,则当 1n k 时,由
3 3
1k k ka a a a a a 知, 1ka a ,因此,当 1n k 时, 1ka a 成立。
故对任意的 *n N , na a 成立。
综上所述,存在常数 0max{ , }M x a ,使得对于任意的 *n N ,都有 na M .
100.(江苏 17)请你设计一个包装盒,如图所示,ABCD 是边长为 60cm 的正方形硬纸片,切去阴影部分
所示的四个全等的等腰直角三角形,再沿虚线折起,使得 ABCD 四个点重合于图中的点 P,正好形成一个
正四棱柱形状的包装盒,E、F 在 AB 上是被切去的等腰直角三角形斜边的两个端点,设 AE=FB=xcm.
(1)若广告商要求包装盒侧面积 S(cm 2 )最大,试问 x 应取何值?
(2)若广告商要求包装盒容积 V(cm 3 )最大,试问 x 应取何值?并求出此时包装盒的高与底面边长的比
值.
【解】(1)根据题意有
2 2 2 260 4 (60 2 ) 240 8S x x x x 28( 15) 1800x (0
0
从而当 x>0,且 x 1 时,f(x)-(
1
ln
x
x +
x
k )>0,即 f(x)>
1
ln
x
x +
x
k .
(ii)设 00,故 'h (x)>0,而
h(1)=0,故当 x(1,
k1
1 )时,h(x)>0,可得 21
1
x h(x)<0,与题设矛盾。
(iii)设 k 1.此时 'h (x)>0,而 h(1)=0,故当 x(1,+ )时,h(x)>0,可得
21
1
x h(x)<0,与题设矛盾。综合得,k 的取值范围为(- ,0]
108.(全国Ⅰ文 21)设函数 21x
xf x e ax
(Ⅰ)若 a= 1
2
,求 xf 的单调区间;
(Ⅱ)若当 x ≥0 时 xf ≥0,求 a 的取值范围
(21)解:
(Ⅰ) 1
2a 时, 21( ) ( 1) 2
xf x x e x , '( ) 1 ( 1)( 1)x x xf x e xe x e x 。当 , 1x 时
'( )f x ;当 1,0x 时, '( ) 0f x ;当 0,x 时, '( ) 0f x 。故 ( )f x 在 , 1 , 0, 单
调增加,在(-1,0)单调减少。
(Ⅱ) ( ) ( 1 )af x x x ax 。令 ( ) 1ag x x ax ,则 '( ) xg x e a 。若 1a ,则当 0,x 时,
'( )g x , ( )g x 为减函数,而 (0) 0g ,从而当 x≥0 时 ( )g x ≥0,即 ( )f x ≥0.
若 a ,则当 0,lnx a 时, '( )g x , ( )g x 为减函数,而 (0) 0g ,从而当 0,lnx a 时 ( )g x <
0,即 ( )f x <0.综合得 a 的取值范围为 ,1
109.(全国Ⅱ理 22)(Ⅰ)设函数 2( ) ln(1 ) 2
xf x x x
,证明:当 x >0 时, ( )f x >0;
(Ⅱ)从编号 1 到 100 的 100 张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取 20 次,设抽
得的 20 个号码互不相同的概率为 p .证明: p < 199( )10
< 2
1
e .
【命题立意】:本小题主要考查函数、导数、不等式证明及等可能事件的概率等知识。通过运用导数知识
解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力.
【解析】(Ⅰ)
2
2 2
1 2( 2) 2( ) 0,( 1)1 ( 2) ( 1)( 2)
x x xf x xx x x x
,(仅当 0x 时 ( ) 0f x )
故函数 ( )f x 在 ( 1, ) 单调递增.当 0x 时, ( ) 0f x ,故当 x >0 时, ( )f x >0.
(Ⅱ)从编号 1 到 100 的 100 张卡片中每次随机抽取一张,然后放回,连续抽取 20 次,则抽得的 20 个号
码互不相同的概率为
20
100
20100
Ap ,要证 p <( 9
10
)19< 2
1
e .
先证:
20
19100
20
9
100 10
Ap ( ) 即证 20
20
100 99 ... 81 100 90
100 90 100
( )
即证 1999 98 ... 81 (90) 而 2 2 299 81 (90 9) (90 9) 90 9 (90)
2 2 298 82 (90 8) (90 8) 90 8 (90)……… 2 2 291 89 (90 1) (90 1) 90 1 (90)
所以 1999 98 ... 81 (90) . 即 199
10p ( )
再证: 19 29
10 e( ) ,即证 19 210
9 e( ) ,即证 10 29
19ln ,即证 10 2
9
ln 19
由(Ⅰ) 2( ) ln(1 ) 2
xf x x x
,当 x >0 时, ( )f x >0.
令 1 ,9x 则
121 1 29ln(1 ) ln(1 ) 019 9 1929
,即 10 2
9
ln 19
综上有: 19 29
10p e ( )
110.(全国Ⅱ文 20)已知函数 3 2( ) 3 (3 6 ) 12 4( )f x x ax a x a a R
(Ⅰ)证明:曲线 ( ) 0y f x x 在 (2,2)的切线过点 ;
(Ⅱ)若 0 0( ) (1,3)f x x x x 在 处取得极小值, ,求 a 的取值范围。
【解析】(Ⅰ) 2( ) 3 6 (3 6 )f x x ax a , (0) 3 6f a ,又 (0) 12 4f a
曲线 ( ) 0y f x x 在 的切线方程是: (12 4) (3 6 )y a a x ,在上式中令 2x ,得 2y
所以曲线 ( ) 0y f x x 在 (2,2)的切线过点 ;
(Ⅱ)由 ( ) 0f x 得 2 2 1 2 0x ax a ,(i)当 2 1 2 1a 时, ( )f x 没有极小值;
(ii)当 2 1a 或 2 1a 时,由 ( ) 0f x 得
2 2
1 22 1, 2 1x a a a x a a a
故 0 2x x 。由题设知 21 2 1 3a a a ,当 2 1a 时,不等式
21 2 1 3a a a 无解;
当 2 1a 时,解不等式 21 2 1 3a a a 得 5 2 12 a
综合(i)(ii)得 a 的取值范围是 5( , 2 1)2
。
111.(山东理 21)某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,
左右两端均为半球形,按照设计要求容器的体积为 80
3
立方米,且 2l r≥ .假设该容器的建造费用仅与其表
面积有关.已知圆柱形部分每平方米建造费用为 3 千元,半球形部分每平方米建造费用为 ( 3)c c> .设该容器
的建造费用为 y 千元.
(Ⅰ)写出 y 关于 r 的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 r .
【 解 析 】( Ⅰ ) 因 为 容 器 的 体 积 为 80
3
立 方 米 , 所 以
3
24
3
r r l 80
3
,解得 2
80 4
3 3
rl r
,所以圆柱的侧面积为
2 rl = 2
80 42 ( )3 3
rr r
2160 8
3 3
r
r
, 两 端 两 个 半 球 的 表 面 积 之 和 为 24 r , 所 以
y 2160 8 rr
+ 24 cr ,定义域为(0,
2
l ).
(Ⅱ)因为 'y 2
160 16 rr
+ 8 cr =
3
2
8 [( 2) 20]c r
r
,所以令 ' 0y 得: 3 20
2r c
; 令 ' 0y
得: 3 200 2r c
,所以 3 20
2r c
米时, 该容器的建造费用最小.
112.(陕西理 21)设函数 ( )f x 定义在 (0, ) 上, (1) 0f ,导函数 1( )f x x
, ( ) ( ) ( )g x f x f x .
(1)求 ( )g x 的单调区间和最小值;
(2)讨论 ( )g x 与 1( )g x
的大小关系;
(3)是否存在 0 0x ,使得 0
1| ( ) ( ) |g x g x x
对任意 0x 成立?若存在,求出 0x 的取值范围;若不存
在,请说明理由.
【分析】(1)先求出原函数 ( )f x ,再求得 ( )g x ,然后利用导数判断函数的单调性(单调区间),并求出
最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;
(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
【解】(1)∵ 1( )f x x
,∴ ( ) lnf x x c ( c 为常数),又∵ (1) 0f ,所以 ln1 0c ,即 0c ,
∴ ( ) lnf x x ; 1( ) lng x x x
,∴ 2
1( ) xg x x
,令 ( ) 0g x ,即 2
1 0x
x
,解得 1x ,
当 (0,1)x 时, ( ) 0g x , ( )g x 是减函数,故区间在 (0,1) 是函数 ( )g x 的减区间;
当 (1, )x 时, ( ) 0g x , ( )g x 是增函数,故区间在 (1, ) 是函数 ( )g x 的增区间;
所以 1x 是 ( )g x 的唯一极值点,且为极小值点,从而是最小值点,
所以 ( )g x 的最小值是 (1) 1g .
(2) 1( ) lng x xx
,设 1 1( ) ( ) ( ) 2lnh x g x g x xx x
,则
2
2
( 1)( ) xh x x
,
当 1x 时, (1) 0h ,即 1( ) ( )g x g x
,当 (0,1) (1, )x 时, ( ) 0h x , (1) 0h ,
因此函数 ( )h x 在 (0, ) 内单调递减,当 0 1x 时, ( ) (1)h x h =0,∴ 1( ) ( )g x g x
;
当 1x 时, ( ) (1)h x h =0,∴ 1( ) ( )g x g x
.
(3)满足条件的 0x 不存在.证明如下:
证法一 假设存在 0 0x ,使 0
1| ( ) ( ) |g x g x x
对任意 0x 成立,
即对任意 0x 有 0
2ln ( ) lnx g x x x
①
但对上述的 0x ,取 0( )
1
g xx e 时,有 1 0ln ( )x g x ,这与①左边的不等式矛盾,
因此不存在 0 0x ,使 0
1| ( ) ( ) |g x g x x
对任意 0x 成立.
证法二 假设存在 0 0x ,使 0
1| ( ) ( ) |g x g x x
对任意 0x 成立,
由(1)知, ( )g x 的最小值是 (1) 1g ,
又 1( ) ln lng x x xx
,而 1x 时, ln x 的值域为 (0, ) ,∴当 1x
时, ( )g x 的值域为[1, ) ,
从而可以取一个值 1 1x ,使 1 0( ) ( ) 1g x g x
,即
1 0( ) ( ) 1g x g x
,∴ 1 0
1
1| ( ) ( ) | 1g x g x x
,这与假设矛盾.∴不存在 0 0x ,使 0
1| ( ) ( ) |g x g x x
对
任意 0x 成立.
113.(陕西文 21)设 ( ) lnf x x , ( ) ( ) ( )g x f x f x .
(1)求 ( )g x 的单调区间和最小值;
(2)讨论 ( )g x 与 1( )g x
的大小关系;
(3)求 a 的取值范围,使得 ( ) ( )g a g x < 1
a
对任意 x >0 成立.
【分析】(1)先求出原函数 ( )f x ,再求得 ( )g x ,然后利用导数判断函数的单调性(单调区间),并求出
最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;
(3)对任意 x >0 成立的恒成立问题转化为函数 ( )g x 的最小值问题.
【解】(1)由题设知 1( ) ln , ( ) lnf x x g x x x
,∴ 2
1( ) ,xg x x
令 ( )g x 0 得 x =1,
当 x ∈(0,1)时, ( )g x <0, ( )g x 是减函数,故(0,1)是 ( )g x 的单调减区间。
当 x ∈(1,+∞)时, ( )g x >0, ( )g x 是增函数,故(1,+∞)是 ( )g x 的单调递增区间,
因此, x =1 是 ( )g x 的唯一极值点,且为极小值点,从而是最小值点,所以 ( )g x 的最小值为 (1) 1.g
(2) 1( ) lng x xx
,设 1 1( ) ( ) ( ) lnh x g x g x xx x
,则
2
2
( 1)( ) xh x x
,
当 1x 时, (1) 0h ,即 1( ) ( )g x g x
,当 (0,1) (1, )x 时, ( ) 0h x ,
因此, ( )h x 在 (0, ) 内单调递减,当 0 1x 时, ( ) (1) 0h x h ,即 1( ) ( ).g x g x
(3)由(1)知 ( )g x 的最小值为 1,所以, 1( ) ( )g a g x a
,对任意 0x ,成立 1( ) 1 ,g a a
即 1,Ina 从而得 0 a e 。
114.(上海理 20) 已知函数 ( ) 2 3x xf x a b ,其中常数 ,a b 满足 0a b
(1)若 0a b ,判断函数 ( )f x 的单调性;
(2)若 0a b ,求 ( 1) ( )f x f x 时的 x 的取值范围.
解:⑴ 当 0, 0a b 时,任意 1 2 1 2, ,x x R x x ,
则 1 2 1 2
1 2( ) ( ) (2 2 ) (3 3 )x x x xf x f x a b
∵ 1 2 1 22 2 , 0 (2 2 ) 0x x x xa a , 1 2 1 23 3 , 0 (3 3 ) 0x x x xb b ,
∴ 1 2( ) ( ) 0f x f x ,函数 ( )f x 在 R 上是增函数。当 0, 0a b 时,同理函数 ( )f x 在 R 上是减函数。
⑵ ( 1) ( ) 2 2 3 0x xf x f x a b , 当 0, 0a b 时 , 3( )2 2
x a
b
, 则 1.5log ( )2
ax b
; 当
0, 0a b 时, 3( )2 2
x a
b
,则 1.5log ( )2
ax b
。
115.(上海文 21)已知函数 ( ) 2 3x xf x a b ,其中常数 ,a b 满足 0a b
(1)若 0a b ,判断函数 ( )f x 的单调性;
(2)若 0a b ,求 ( 1) ( )f x f x 时的 x 的取值范围.
解:⑴ 当 0, 0a b 时,任意 1 2 1 2, ,x x R x x ,
则 1 2 1 2
1 2( ) ( ) (2 2 ) (3 3 )x x x xf x f x a b
∵ 1 2 1 22 2 , 0 (2 2 ) 0x x x xa a , 1 2 1 23 3 , 0 (3 3 ) 0x x x xb b ,
∴ 1 2( ) ( ) 0f x f x ,函数 ( )f x 在 R 上是增函数。当 0, 0a b 时,同理函数 ( )f x 在 R 上是减函数。
⑵ ( 1) ( ) 2 2 3 0x xf x f x a b
当 0, 0a b 时, 3( )2 2
x a
b
,则 1.5log ( )2
ax b
;
当 0, 0a b 时, 3( )2 2
x a
b
,则 1.5log ( )2
ax b
。
116.(四川理 22)已知函数 2 1( ) 3 2f x x , ( )h x x .
(Ⅰ)设函数 F(x)=f(x)-h(x),求 F(x)的单调区间与极值;
(Ⅱ)设 aR ,解关于 x 的方程 4 2 2
3 3log [ ( 1) ] log ( ) log (4 )2 4f x h a x h x ;
(Ⅲ)试比较
100
1
(100) (100) ( )
k
f h h k
与 1
6
的大小.
本小题主要考查函数导数的应用、不等式的证明、解方程等基本知识,考查数形结合、函数与方程、分类
与整合、特殊与一般等数学思想方法及推理运算、分析问题、解决问题的能力.
解:(Ⅰ)由 2 1( ) 3 2F x x x ( 0x )知, 4 3( )
6
xF x
x
,令 ( ) 0F x ,得 9
16x .
当 9(0, )16x 时, ( ) 0F x ;当 9( , )16x 时, ( ) 0F x .
故当 9[0, )16x 时, ( )F x 是减函数; 9[ , )16x 时, ( )F x 是增函数.
函数 ( )F x 在 9
16x 处有得极小值 9 1( )16 8F .
(Ⅱ)方法一:原方程可化为 4 2 2
3 3log [ ( 1) ] log ( ) log (4 )2 4f x h a x h x ,
即为 4 2 2 2log ( 1) log log 4 log
4
a xx a x x
x
,且 ,
1 4,
x a
x
①当1 4a 时,1 x a ,则 1 4
a xx x
,即 2 6 4 0x x a ,
36 4( 4) 20 4 0a a ,此时 6 20 4 3 52
ax a ,∵1 x a ,
此时方程仅有一解 3 5x a .
②当 4a 时,1 4x ,由 1 4
a xx x
,得 2 6 4 0x x a , 36 4( 4) 20 4a a ,
若 4 5a ,则 0 ,方程有两解 3 5x a ;
若 5a 时,则 0 ,方程有一解 3x ;
若 1a 或 5a ,原方程无解.
方法二:原方程可化为 4 2 2log ( 1) log (4 ) log ( )x h x h a x ,
即 2 2 2
1 log ( 1) log 4 log2 x x a x ,
1 0,
4 0,
0,
( 1)(4 ) .
x
x
a x
x x a x
2
1 4
,
( 3) 5.
x
x a
a x
①当1 4a 时,原方程有一解 3 5x a ;
②当 4 5a 时,原方程有二解 3 5x a ;
③当 5a 时,原方程有一解 3x ;
④当 1a 或 5a 时,原方程无解.
(Ⅲ)由已知得
100 100
1 1
( )
k k
h k k
.
设数列{ }na 的前 n 项和为 nS ,且 1( ) ( ) 6nS f n h n ( *nN )
从而 1 1 1a S ,当 2 100k 时, 1
4 3 4 1 16 6k k k
k ka S S k k
.
又 1[(4 3) (4 1) 1]6ka k k k k k
2 21 (4 3) (4 1) ( 1)
6 (4 3) (4 1) 1
k k k k
k k k k
1 1 06 (4 3) (4 1) 1k k k k
.
即对任意 2 100k 时,有 ka k ,又因为 1 1 1a ,所以
100 100
1 1
k
k k
a k
.
故
100
1
1(100) (100) ( ) 6k
f h h k
.
117.(四川文 22)已知函数 2 1( ) 3 2f x x , ( )h x x .
(Ⅰ)设函数 F(x)=18f(x)-x2[h(x)]2,求 F(x)的单调区间与极值;
(Ⅱ)设 aR ,解关于 x 的方程 3 3lg[ ( 1) ] 2lg ( ) 2lg (4 )2 4f x h a x h x ;
(Ⅲ)设 *nN ,证明: 1( ) ( ) [ (1) (2) ( )] 6f n h n h h h n .
本小题主要考查函数导数的应用、不等式的证明、解方程等基础知识,考查数形结合、函数与方程、分类
与整合等数学思想方法及推理运算、分析问题、解决问题的能力.
解:(Ⅰ) 2 2 3( ) 18 ( ) [ ( )] 12 9( 0)F x f x x h x x x x ,
2( ) 3 12F x x .
令 ( ) 0F x ,得 2x ( 2x 舍去).
当 (0,2)x 时. ( ) 0F x ;当 (2, )x 时, ( ) 0F x ,
故当 [0,2)x 时, ( )F x 为增函数;当 [2, )x 时, ( )F x 为减函数.
2x 为 ( )F x 的极大值点,且 (2) 8 24 9 25F .
(Ⅱ)方法一:原方程可化为 4 2 2
3 3log [ ( 1) ] log ( ) log (4 )2 4f x h a x h x ,
即为 4 2 2 2log ( 1) log log 4 log
4
a xx a x x
x
,且 ,
1 4,
x a
x
①当1 4a 时,1 x a ,则 1 4
a xx x
,即 2 6 4 0x x a ,
36 4( 4) 20 4 0a a ,此时 6 20 4 3 52
ax a ,∵1 x a ,
此时方程仅有一解 3 5x a .
②当 4a 时,1 4x ,由 1 4
a xx x
,得 2 6 4 0x x a , 36 4( 4) 20 4a a ,
若 4 5a ,则 0 ,方程有两解 3 5x a ;
若 5a 时,则 0 ,方程有一解 3x ;
若 1a 或 5a ,原方程无解.
方法二:原方程可化为 4 2 2log ( 1) log (4 ) log ( )x h x h a x ,
即 2 2 2
1 log ( 1) log 4 log2 x x a x ,
1 0,
4 0,
0,
( 1)(4 ) .
x
x
a x
x x a x
2
1 4
,
( 3) 5.
x
x a
a x
①当1 4a 时,原方程有一解 3 5x a ;
②当 4 5a 时,原方程有二解 3 5x a ;
③当 5a 时,原方程有一解 3x ;
④当 1a 或 5a 时,原方程无解.
(Ⅲ)由已知得 (1) (2) ( )] 1 2h h h n n ,
1 4 3 1( ) ( ) 6 6 6
nf n h n n .
设数列{ }na 的前 n 项和为 nS ,且 1( ) ( ) 6nS f n h n ( *nN )
从而有 1 1 1a S ,当 2 100k 时, 1
4 3 4 1 16 6k k k
k ka S S k k
.
又 1[(4 3) (4 1) 1]6ka k k k k k
2 21 (4 3) (4 1) ( 1)
6 (4 3) (4 1) 1
k k k k
k k k k
1 1 06 (4 3) (4 1) 1k k k k
.
即对任意 2k 时,有 ka k ,又因为 1 1 1a ,所以 1 2 1 2na a a n .
则 (1) (2) ( )nS h h h n ,故原不等式成立.
118.(天津理 21)已知函数 e xf x x xR .
(Ⅰ)求函数 f x 的单调区间和极值;
(Ⅱ)已知函数 y g x 的图象与函数 y f x 的图象关于直线 1x
对称.证明当 1x 时, f x g x .
(Ⅲ)如果 1 2x x ,且 1 2f x f x ,证明 1 2 2x x .
【解】(Ⅰ) 1 e xf x x .令 1 e 0xf x x ,则 1x .
当 x 变化时, ,f x f x 的变化情况如下表:
x ,1 1 1,
f x 0
f x 增 极大值 减
所以 f x 在区间 ,1 内是增函数,在区间 1, 内是减函数.
函数 f x 在 1x 处取得极大值 1f .且 11 ef .
(Ⅱ)因为函数 y g x 的图象与函数 y f x 的图象关于直线 1x 对称,
所以 2g x f x ,于是 22 exg x x .
记 F x f x g x ,则 2e 2 ex xF x x x , 2 21 e 1 ex xF x x ,
当 1x 时, 2 2 0x ,从而 2 2e 1 0x ,又 e 0x ,所以 0F x ,
于是函数 F x 在区间 1, 上是增函数.
因为 1 11 e e 0F ,所以,当 1x 时, 1 0F x F .因此 f x g x .
(Ⅲ)(1) 若 1 21 1 0x x ,由(Ⅰ)及 1 2f x f x ,得 1 2x x ,与 1 2x x 矛盾;
(2) 若 1 21 1 0x x ,由由(Ⅰ)及 1 2f x f x ,得 1 2x x ,与 1 2x x 矛盾;
根据(1),(2)可得 1 21 1 0x x .不妨设 1 21, 1x x .
由(Ⅱ)可知 2 2 22f x g x f x ,所以 1 2 2 22f x f x g x f x .
因为 2 1x ,所以 22 1x ,又 1 1x ,由(Ⅰ), f x 在区间 ,1 内是增函数,
所以 1 22x x ,即 1 2 2x x .
119.(天津文 20)已知函数 3 23 12f x ax x xR ,其中 0a .
(Ⅰ)若 1a ,求曲线 y f x 在点 2, 2f 处的切线方程;
(Ⅱ)若在区间 1 1,2 2
上, 0f x 恒成立,求 a 的取值范围.
【解】(Ⅰ)当 1a 时, 3 23 12f x x x , 2 3f . 23 3f x x x , 2 6f .
所以曲线 y f x 在点 2, 2f 处的切线方程为 3 6 2y x ,即 6 9y x .
(Ⅱ) 23 3 3 1f x ax x x ax .
令 0f x ,解得 0x 或 1x a
.针对区间 1 1,2 2
,需分两种情况讨论:
(1) 若 0 2a ,则 1 1
2a
.
当 x 变化时, ,f x f x 的变化情况如下表:
x 1 ,02
0 10, 2
f x 0
f x 增 极大值 减
所以 f x 在区间 1 1,2 2
上的最小值在区间的端点得到.因此在区间 1 1,2 2
上, 0f x 恒成立,
等价于
1 0,2
1 0,2
f
f
即
5 0,8
5 0,8
a
a
解得 5 5a ,又因为 0 2a ,所以 0 2a .
(2) 若 2a ,则 1 10 2a
.
当 x 变化时, ,f x f x 的变化情况如下表:
x 1 ,02
0 10, a
1
a
1 1, 2a
f x 0 0
f x 增 极大值 减 极小值 增
所以 f x 在区间 1 1,2 2
上的最小值在区间的端点或 1x a
处得到.
因此在区间 1 1,2 2
上, 0f x 恒成立,等价于
1 0,2
1 0,
f
f a
即
2
5 0,8
11 0,
2
a
a
解得 2 52 a 或 2
2a ,又因为 2a ,所以 2 5a .
综合(1),(2), a 的取值范围为 0 5a .
120.(浙江理 22)已知函数 ( ) 2 ln(1 ) ( 0)f x a x x a .
(Ⅰ)求 ( )f x 的单调区间和极值;
(Ⅱ)求证:
(1 )lg lg lg4lg lg ( 1)2 3
n
n
n
ne e ee e nn
*( )n N .
解:(Ⅰ)定义域为 1, , 2'( ) 11
af x x
………2 分
令 '( ) 0 1 2 1f x x a ,令 '( ) 0 2 1f x x a
故 ( )f x 的单调递增区间为 1,2 1a , ( )f x 的单调递减区间为 2 1,a
( )f x 的极大值为 2 ln 2 2 1a a a
(Ⅱ)证:要证
(1 )lg lg lg4lg lg ( 1)2 3
n
n
n
ne e ee e nn
即证
(1 )
1 1 1 lg ( 1)4 2 3 lg
nn
nne n
n e
, 即证
(1 )
1 1 14 ln ( 1)2 3
nn
nne nn
即证 1 1 1 11 3 ln( 1) (1 )2 3
nnn n
令 1
2a ,由(Ⅰ)可知 ( )f x 在 (0, ) 上递减,故 ( ) (0) 0f x f
即 ln(1 )x x ,令 *1 ( )x n Nn
,故 1 1 1ln(1 ) ln ln( 1) lnn n nn n n
累加得, 1 1 1ln( 1) 1 2 3n n
1 1 1 1ln(1 ) ln(1 ) 1 (1 ) 3n n en n n n
故 1 1 1 11 3 ln( 1) (1 )2 3
nnn n
,得证
法二: 1(1 )n
n
= 0 1 2
2
1 1 1n
n n n n nC C C Cn n n
1 1 12 2! 3! !n
2
1 1 12 2 2 2n
1
1
1 1(1 ) 12 22 3 31 21 2
n
n
,其余相同证法.
121.(浙江文 21)设函数 axxxaxf 22 ln)( , 0a
(Ⅰ)求 )(xf 的单调区间;
(Ⅱ)求所有实数 a ,使 2)(1 exfe 对 ],1[ ex 恒成立.
注: e 为自然对数的底数.
(21)本题主要考查函数的单调性、导数运算法则、导数应用等基础知识,同时考查抽象概括、推理论证
能力。满分 15 分。
(Ⅰ)解:因为 2 2( ) ln . 0f x a x x ax x 其中 ,所以
2 ( )(2 )( ) 2a x a x af x x ax x
由于 0a ,所以 ( )f x 的增区间为 (0, )a ,减区间为 ( , )a
(Ⅱ)证明:由题意得, (1) 1 1,f a c a c 即 ,由(Ⅰ)知 ( ) [1, ]f x e在 内单调递增,
要使 21 ( ) [1, ]e f x e x e 对 恒成立,只要 2 2 2
(1) 1 1,
( )
f a e
f e a e ae e
,解得 .a e
122.(重庆理 18)设 ( )f x x ax bx 的导数 '( )f x 满足 '( ) , '( )f a f b ,其中常数 ,a b R 。
(Ⅰ)求曲线 ( )y f x 在点 ( , ( ))f 处的切线方程;
(Ⅱ) 设 ( ) '( ) xg x f x e ,求函数 ( )g x 的极值。
解:(Ⅰ) / 2( ) 3 2f x x ax b 则 / (1) 3 2 2 3f a b a b ;
/ 3(2) 12 4 2f a b b a ;所以 3 23( ) 3 12f x x x x ,于是有 /5(1) , (1) 32f f
故曲线 ( )y f x 在点 ( , ( ))f 处的切线方程为: 6 2 1 0x y
(Ⅱ)由(Ⅰ)知 2 / 2( ) (3 3 3) ( ) ( 3 9 )x xg x x x e g x x x e ,令
/
1 2( ) 0 0, 3g x x x ;
于是函数 ( )g x 在 ( ,0) 上递减, (0,3) 上递增, (3, ) 上递减;
所以函数 ( )g x 在 0x 处取得极小值 (0) 3g ,在 3x 处取得极大值
3(3) 15g e 。
123. (重庆文 19)设 的导数为 ,若函数 的图象关于直线
对称,且 .](Ⅰ)求实数 , 的值;(Ⅱ)求函数 的极值
解:(Ⅰ)
2
/ 2 2( ) 6 2 6( )6 6
a af x x ax b x b ,函数 的图象关于直线
6
ax 对称,
所以 1 36 2
a a ,又 / (1) 0 6 2 0 12f a b b ;
(Ⅱ)由(Ⅰ) 3 2 / 2( ) 2 3 12 1, ( ) 6 6 12f x x x x f x x x ,
令 /
1 2( ) 0 2, 1f x x x ;
函数 ( )f x 在 ( , 2) 上递增,在 ( 2,1) 上递减,在 (1, ) 上递增,所以函数 ( )f x 在 2x 处取得极大
值 ( 2) 21f ,在 1x 处取得极大值 (1) 6f 。
2010 年高考题
选择题
1.(2010 湖南文)函数 y=ax2+ bx 与 y= | |
log b
a
x (ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是
答案 D
2. ( 2010 浙 江
理)设函数的集
合
2
1 1( ) log ( ) ,0, ,1; 1,0,12 2P f x x a b a b
,
平面上点的集合
1 1( , ) ,0, ,1; 1,0,12 2Q x y x y
,
则在同一直角坐标系中, P 中函数 ( )f x 的图象恰好经过Q 中两个点的函数的个数是
(A)4 (B)6 (C)8 (D)10
答案 B
解析:当 a=0,b=0;a=0,b=1;a=
2
1 ,b=0; a=
2
1 ,b=1;a=1,b=-1;a=1,b=1 时满足题意,故答案选 B,本题主要考察
了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的
考察,属中档题
3.(2010 辽宁文)已知 0a ,函数 2( )f x ax bx c ,若 0x 满足关于 x 的方程 2 0ax b ,则下列选
项的命题中为假命题的是
(A) 0, ( ) ( )x R f x f x (B) 0, ( ) ( )x R f x f x
(C) 0, ( ) ( )x R f x f x (D) 0, ( ) ( )x R f x f x
答案 C
解析:选 C.函数 ( )f x 的最小值是 0( ) ( )2
bf f xa
等价于 0, ( ) ( )x R f x f x ,所以命题 C 错误.
4.(2010 江西理)给出下列三个命题:
①函数 1 1 cosln2 1 cos
xy x
与 ln tan 2
xy 是同一函数;②若函数 y f x 与 y g x 的图像关于直线
y x 对称,则函数 2y f x 与 1
2y g x 的图像也关于直线 y x 对称;
③若奇函数 f x 对定义域内任意 x 都有 (2 )f x f x ,则 f x 为周期函数。
其中真命题是
A. ①② B. ①③ C.②③ D. ②
答案 C
【解析】考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除 A、B,验证
③, [2 ( )] (2 )f x f x f x ,又通过奇函数得 ( )f x f x ,所以 f(x)是周期为 2 的周期函
数,选择 C。
5.(2010 重庆理)函数 4 1
2
x
xf x 的图象
A.关于原点对称 B.关于直线 y=x 对称
C.关于 x 轴对称 D.关于 y 轴对称
答案 D
解析: )(
2
41
2
14)( xfxf x
x
x
x
)(xf 是偶函数,图像关于 y 轴对称
6.(2010 天津文)下列命题中,真命题是
(A) m R, f x x mx x R 2使函数 ( )= ( )是偶函数
(B) m R, f x x mx x R 2使函数 ( )= ( )是奇函数
(C) m R, f x x mx x R 2使函数 ( )= ( )都是偶函数
(D) m R, f x x mx x R 2使函数 ( )= ( )都是奇函数
答案 A
【解析】本题主要考查奇偶数的基本概念,与存在量词、全称量词的含义,属于容易题。当 m=0 时,函数
f(x)=x2 是偶函数,所以选 A.
【温馨提示】本题也可以利用奇偶函数的定义求解。
7.(2010 天津理)命题“若 f(x)是奇函数,则 f(-x)是奇函数”的否命题是
(A)若 f(x) 是偶函数,则 f(-x)是偶函数
(B)若 f(x)不是奇函数,则 f(-x)不是奇函数
(C)若 f(-x)是奇函数,则 f(x)是奇函数
(D)若 f(-x)不是奇函数,则 f(x)不是奇函数
答案 B
【解析】本题主要考查否命题的概念 ,属于容易题。
否命题是同时否定命题的条件结论,故否命题的定义可知 B 项是正确的。
【温馨提示】解题时要注意否命题与命题否定的区别。
8.(2010 广东理)若函数 f(x)=3x+3-x 与 g(x)=3x-3-x 的定义域均为 R,则
A.f(x)与 g(x)均为偶函数 B. f(x)为偶函数,g(x)为奇函数
C.f(x)与 g(x)均为奇函数 D. f(x)为奇函数,g(x)为偶函数
答案 D
【解析】 ( ) 3 3 ( ), ( ) 3 3 ( )x x x xf x f x g x g x .
9.(2010 广东文)若函数 xxxf 33)( 与 xxxg 33)( 的定义域均为 R,则
A. )(xf 与 )(xg 与均为偶函数 B. )(xf 为奇函数, )(xg 为偶函数
C. )(xf 与 )(xg 与均为奇函数 D. )(xf 为偶函数, )(xg 为奇函数
答案 D
解:由于 )(33)( )( xfxf xx ,故 )(xf 是偶函数,排除 B、C
由题意知,圆心在 y 轴左侧,排除 A、C
在 AORt 0 ,
2
1
0
kA
OA ,故 50
5
1
0
5
0
0 OOO
A ,选 D
10.(2010 广东文)函数 )1lg()( xxf 的定义域是
A. ),2( B. ),1( C. ),1[ D. ),2[
答案 B
解: 01 x ,得 1x ,选 B.
11.(2010 全国卷 1 理)已知函数 f(x)=|lgx|.若 00,y>0,函数 f(x)满足 f(x+y)=f(x)f
(y)”的是
(A)幂函数 (B)对数函数 (C)指数函数 (D)余弦函数
答案 C
【解析】本题考查幂的运算性质
)()()( yxfaaayfxf yxyx
20.(2010 辽宁文)设 2 5a b m ,且 1 1 2a b
,则 m
(A) 10 (B)10 (C)20 (D)100
答案 A
【解析】选 A. 21 1 log 2 log 5 log 10 2, 10,m m m ma b
又 0, 10.m m
21.(2010 全国卷 2 文)函数 y=1+ln(x-1)(x>1)的反函数是
(A)y= 1xe -1(x>0) (B) y= 1xe +1(x>0)
(C) y= 1xe -1(x R) (D)y= 1xe +1 (x R)
答案 D
【 解 析 】 D : 本 题 考 查 了 函 数 的 反 函 数 及 指 数 对 数 的 互 化 , ∵ 函 数 y=1+ln ( x-1 ) (x>1) , ∴
1 1ln( 1) 1, 1 , 1y xx y x e y e
22.(2010 安徽文)设
2 3 2
5 5 53 2 2
5 5 5a b c ( ), ( ), ( ),则 a,b,c 的大小关系是
(A)a>c>b (B)a>b>c (C)c>a>b (D)b>c>a
答案 A
【解析】 2
5y x 在 0x 时是增函数,所以 a c , 2( )5
xy 在 0x 时是减函数,所以 c b 。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.
23.(2010 安徽文)设 0abc ,二次函数 2( )f x ax bx c 的图像可能是
答案 D
【解析】当 0a 时,b 、 c 同号,(C)(D)两图中 0c ,故 0, 02
bb a
,选项(D)符合
【方法技巧】根据二次函数图像开口向上或向下,分 0a 或 0a 两种情况分类考虑.另外还要注意 c 值
是抛物线与 y 轴交点的纵坐标,还要注意对称轴的位置或定点坐标的位置等.
24.(2010 浙江文)已知函数 1( ) log ( 1),f x x 若 ( ) 1,f =
(A)0 (B)1 (C)2 (D)3
答案 B
【解析】 +1=2,故 =1,选 B,本题主要考察了对数函数概念及其运算性质,属容易题
25.(2010 山东文)函数 2log 3 1xf x 的值域为
A. 0, B. 0, C. 1, D. 1,
答案 A
26.(2010 北京文)给定函数① 1
2y x ,② 1
2
log ( 1)y x ,③ | 1|y x ,④ 12xy ,期中在区间(0,
1)上单调递减的函数序号是
(A)①② (B)②③ (C)③④ (D)①④
答案 B
27.(2010 北京文)若 a,b 是非零向量,且 a b , a b ,则函数 ( ) ( ) ( )f x xa b xb a 是
(A)一次函数且是奇函数 (B)一次函数但不是奇函数
(C)二次函数且是偶函数 (D)二次函数但不是偶函数
答案 A
28.(2010 四川理)2log510+log50.25=
(A)0 (B)1 (C) 2 (D)4
解析:2log510+log50.25
=log5100+log50.25
=log525
=2
答案 C
29.(2010 天津文)设 5
5 4a log 4 b log c log 2
5, ( 3), ,则
(A)af(1)=1+1=2,即 a+b 的取值范围是(2,+∞).
【解析 2】由 00,所以零点在区间(0,1)上,选 C
【温馨提示】函数零点附近函数值的符号相反,这类选择题通 常 采 用
代入排除的方法求解。
44.(2010 天津理)若函数 f(x)=
2
1
2
log , 0,
log ( ), 0
x x
x x
,若 f(a)>f(-a),则实数 a 的取值范围是
(A)(-1,0)∪(0,1) (B)(-∞,-1)∪(1,+∞)
(C)(-1,0)∪(1,+∞) (D)(-∞,-1)∪(0,1)
【答案】C
【解析】本题主要考查函数的对数的单调性、对数的基本运算及分类讨论思想,属于中等题。
由分段函数的表达式知,需要对 a 的正负进行分类讨论。
2 1 1 2
2 2
0 a<0
( ) ( ) log log log ( ) log ( )
a
f a f a a a a a
或
00
1 -1 011
2
aa
a a
aa a
或 或
【温馨提示】分类函数不等式一般通过分类讨论的方式求解,解对数不等式既要注意真数大于 0,同事要
注意底数在(0,1)上时,不等号的方向不要写错。
45.(2010 天津理)函数 f(x)= 2 3x x 的零点所在的一个区间是
(A)(-2,-1)(B)(-1,0)(C)(0,1)(D)(1,2)
【答案】B
【解析】本题主要考查函数零点的概念与零点定理的应用,属于容易题。
由 1( 1) 3 0, (0) 1 02f f 及零点定理知 f(x)的零点在区间(-1,0)上。
【温馨提示】函数零点附近函数值的符号相反,这类选择题通常采用代入排除的方法求解。
46.(2010 福建文)函数
2x +2x-3,x 0x)=
-2+ln x,x>0
f
( 的零点个数为 ( )
A.3 B.2 C.1 D.0
【答案】B
【解析】当 0x 时,令 2 2 3 0x x 解得 3x ;
当 0x 时,令 2 ln 0x 解得 100x ,所以已知函数有两个零点,选 C。
【命题意图】本题考查分段函数零点的求法,考查了分类讨论的数学思想。
47.(2010 湖北文)3.已知函数 3log , 0
( )
2 , 0x
x x
f x
x
,则 1( ( ))9f f
A.4 B. 1
4 C.-4 D- 1
4
【答案】B
【解析】根据分段函数可得 3
1 1( ) log 29 9f ,则 21 1( ( )) ( 2) 29 4f f f ,
所以 B 正确.
48.(2010 全国卷 2 理)若曲线 1
2y x
在点
1
2,a a
处的切线与两个坐标围成的三角形的面积为 18,则 a
(A)64 (B)32 (C)16 (D)8
【答案】A
【命题意图】本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的
计算能力..
【解析】
3 3
2 21 1' ,2 2y x k a
,切线方程是
1 3
2 21 ( )2y a a x a
,令 0x ,
1
23
2y a
,令 0y ,
3x a ,∴三角形的面积是
1
21 33 182 2s a a
,解得 64a .故选 A.
49.(2010 辽宁文)已知点 P 在曲线 4
1xy e
上, 为曲线在点 P 处的切线的倾斜角,则 的取值范围
是
(A)[0,
4
) (B)[ , )4 2
(C) 3( , ]2 4
(D) 3[ , )4
答案 D
解析:选 D. 2
4 4
12 1 2
x
x x
x
x
ey e e e e
, 1 2, 1 0x
xe ye
,
即 1 tan 0 , 3[ , )4
50.(2010 辽宁理)已知点 P 在曲线 y= 4
1xe
上,a 为曲线在点 P 处的切线的倾斜角,则 a 的取值范围是
(A)[0,
4
) (B)[ , )4 2
(C) 3( , ]2 4
(D) 3[ , )4
【答案】D
【命题立意】本题考查了导数的几何意义,求导运算以及三角函数的知识。
【解析】因为 '
2
4 4 1( 1) 2
x
x x x
ey e e e
,即 tan a≥-1,所以 3
4
51.(2010 全国卷 2 文)若曲线 2y x ax b 在点 (0, )b 处的切线方程是 1 0x y ,则
(A) 1, 1a b (B) 1, 1a b
(C) 1, 1a b (D) 1, 1a b
【解析】A:本题考查了导数的几何意思即求曲线上一点处的切线方程
∵ 02 xy x a a ,∴ 1a , (0, )b 在切线 1 0x y ,∴ 1b
52.(2010 江西理)如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记 t 时刻五角星露
出水面部分的图形面积为 0 0S t S ,则导函数 'y S t 的图像大致为
【答案】A
【解析】本题考查函数图像、导
数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。最初零时刻和最后终点时刻
没有变化,导数取零,排除 C;总面积一直保持增加,没有负的改变量,排除 B;考察 A、D 的差异在于
两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择 A。
二、填空题
53.(2010 重庆文数)已知 0t ,则函数
2 4 1t ty t
的最小值为____________ .
答案 -2
解析:
2 4 1 1 4 2( 0)t ty t tt t
,当且仅当 1t 时, min 2y
54.(2010 广东理)函数 ( )f x =lg( x -2)的定义域是 .
答案(1,+∞) .
【解析】∵ 1 0x ,∴ 1x .
55.(2010 全国卷 1 理)直线 1y 与曲线 2y x x a 有四个交点,则 a 的取值范围是 .
56.(2010 福建理)已知定义域为 0 ( , )的函数 f(x) 满足:①对任意 x 0 ( , ),恒有 f(2x)=2f(x) 成
立;当 x ](1,2 时, f(x)=2-x 。给出如下结论:
①对任意 m Z ,有 mf(2 )=0 ;②函数 f(x) 的值域为[0 , );③存在 n Z ,使得 nf(2 +1)=9 ;④“函
数 f(x) 在区间 ( , )a b 上单调递减”的充要条件是 “存在 Zk ,使得
1( , ) (2 ,2 )k ka b ”。
其中所有正确结论的序号是 。
【答案】①②④
【解析】对①,因为 m2 >0 ,所以 mf(2 )=0 ,故①正确;经分析,容易得出②④也正确。
【命题意图】本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。
57.(2010 江苏卷)设函数 f(x)=x(ex+ae-x)(xR)是偶函数,则实数 a=________________
答案 a=-1
【解析】考查函数的奇偶性的知识。g(x)=ex+ae-x 为奇函数,由 g(0)=0,得 a=-1。
58.(2010 上海文)9.函数 3( ) log ( 3)f x x 的反函数的图像与 y 轴的交点坐标是 。
答案 (0,2)
解析:考查反函数相关概念、性质
法一:函数 3( ) log ( 3)f x x 的反函数为 33 xy ,另 x=0,有 y=-2
法二:函数 3( ) log ( 3)f x x 图像与 x 轴交点为(-2,0),利用对称性可知,函数 3( ) log ( 3)f x x 的反
函数的图像与 y 轴的交点为(0,-2)
59.(2010 上海文)14.将直线 1 : 1 0l x y 、 2 : 0l nx y n 、 3 : 0l x ny n ( *n N , 2n )
围成的三角形面积记为 nS ,则 lim nn
S
。
【答案】 1
2
【解析】B )1,1( n
n
n
n 所以 BO⊥AC,
nS =
)1(2
1)2
221(22
1
n
n
n
n
所以 lim nn
S
1
2
60.(2010 湖南文)10.已知一种材料的最佳加入量在 100g 到 200g 之间,若用 0.618 法安排试验,则第一
次试点的加入量可以是 g
【答案】171.8 或 148.2
【解析】根据 0.618 法,第一次试点加入量为
110+(210-110)0.618=171.8
或 210-(210-110)0.618=148.2
【命题意图】本题考察优选法的 0.618 法,属容易题。
61.(2010 陕西文)13.已知函数 f(x)= 2
3 2, 1,
, 1,
x x
x ax x
若 f(f(0))=4a,则实数 a= .
答案 2
【解析】f(0)=2,f(f(0))=f(2)=4+2a=4a,所以 a=2
62.(2010 重庆理)(15)已知函数 f x 满足: 11 4f ,
4 ,f x f y f x y f x y x y R ,则 2010f =_____________.
解析:取 x=1 y=0 得
2
1)0( f
法一:通过计算 )........4(),3(),2( fff ,寻得周期为 6
法二:取 x=n y=1,有 f(n)=f(n+1)+f(n-1),同理 f(n+1)=f(n+2)+f(n)
联立得 f(n+2)= —f(n-1) 所以 T=6 故 2010f =f(0)=
2
1
63.(2010 天津文)(16)设函数 f(x)=x- 1
x ,对任意 x [1, ),f(mx)+mf(x)<0 恒成立,则实数 m 的取
值范围是________
【答案】m<-1
【解析】本题主要考查了恒成立问题的基本解法及分类讨论思想,属于难题。
已知 f(x)为增函数且 m≠0
若 m>0,由复合函数的单调性可知 f(mx)和 mf(x)均为增函数,此时不符合题意。
M<0,时有 2
2
1 1 1 10 2 ( ) 0 1 2mmx mx mx m xmx x m x m
因为 22y x 在 [1, )x
上的最小值为 2,所以 1+ 2
1 2m
即 2m >1,解得 m<-1.
【温馨提示】本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求
解。
64.(2010 浙江文)(16) 某商家一月份至五月份累计销售额达 3860 万元,预测六月份销售额为 500 万元,
七月份销售额比六月份递增 x%,八月份销售额比七月份递增 x%,九、十月份销售总额与七、八月份销售
总额相等,若一月至十月份销售总额至少至少达 7000 万元,则,x 的最小值 。
答案 20
65. ( 2010 天 津 理 数 ) ( 16 ) 设 函 数 2( ) 1f x x , 对 任 意 2 ,3x
,
24 ( ) ( 1) 4 ( )xf m f x f x f mm
恒成立,则实数 m 的取值范围是 .
【解析】本题主要考查函数恒成立问题的基本解法,属于难题。
依 据 题 意 得
2
2 2 2 2
2 1 4 ( 1) ( 1) 1 4( 1)x m x x mm
在 3[ , )2x 上 恒 定 成 立 , 即
2
2 2
1 3 24 1mm x x
在 3[ , )2x 上恒成立。
当 3
2x 时函数 2
3 2 1y x x
取得最小值 5
3
,所以 2
2
1 54 3mm
,即
2 2(3 1)(4 3) 0m m ,解得 3
2m 或 3
2m
【温馨提示】本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求
解
66.(2010 广东文数)
67.(2010 江苏卷)11、已知函数
2 1, 0( )
1, 0
x xf x
x
,则满足不等式 2(1 ) (2 )f x f x 的 x 的范围是_____。
【解析】 考查分段函数的单调性。
2
2
1 2 ( 1, 2 1)
1 0
x x x
x
68.(2010 江苏卷)14、将边长为 1m 正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,
记
2(S 梯形的周长)
梯形的面积 ,则 S 的最小值是________。
【解析】 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为 x ,则:
2 2
2
(3 ) 4 (3 ) (0 1)11 3 3( 1) (1 )2 2
x xS xxx x
(方法一)利用导数求函数最小值。
2
2
4 (3 )( ) 13
xS x x
,
2 2
2 2
4 (2 6) (1 ) (3 ) ( 2 )( ) (1 )3
x x x xS x x
2 2
2 2 2 2
4 (2 6) (1 ) (3 ) ( 2 ) 4 2(3 1)( 3)
(1 ) (1 )3 3
x x x x x x
x x
1( ) 0,0 1, 3S x x x ,
当 1(0, ]3x 时, ( ) 0,S x 递减;当 1[ ,1)3x 时, ( ) 0,S x 递增;
故当 1
3x 时,S 的最小值是 32 3
3
。
(方法二)利用函数的方法求最小值。
令 1 1 13 , (2,3), ( , )3 2x t t t
,则:
2
2
2
4 4 1
8 66 83 3 1
tS t t
t t
故当 1 3 1,8 3xt
时,S 的最小值是 32 3
3
。
三、解答题
69.(2010 上海文)(本题满分 16 分)本题共有 3 个小题,第 1 小题满分 3 分,第 2 小题满分 5 分,第 3
小题满分 8 分。
若实数 x 、 y 、 m 满足 x m y m ,则称 x 比 y 接近 m .
(1)若 2 1x 比 3 接近 0,求 x 的取值范围;
(2)对任意两个不相等的正数 a 、b ,证明: 2 2a b ab 比 3 3a b 接近 2ab ab ;
(3)已知函数 ( )f x 的定义域 , ,D x x k k Z x R .任取 x D , ( )f x 等于1 sin x 和1 sin x 中
接近 0 的那个值.写出函数 ( )f x 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要
求证明).
解析:(1) x(2,2);
(2) 对任意两个不相等的正数 a、b,有 2 2 2a b ab ab ab , 3 3 2a b ab ab ,
因为 2 2 3 3 2| 2 | | 2 | ( )( ) 0a b ab ab ab a b ab ab a b a b ,
所以 2 2 3 3| 2 | | 2 |a b ab ab ab a b ab ab ,即 a2bab2 比 a3b3 接近 2ab ab ;
(3)
1 sin , (2 ,2 )( ) 1 | sin |,1 sin , (2 ,2 )
x x k kf x x x kx x k k
,kZ,
f(x)是偶函数,f(x)是周期函数,最小正周期 T,函数 f(x)的最小值为 0,
函数 f(x)在区间[ , )2k k 单调递增,在区间 ( , ]2k k 单调递减,kZ.
70.(2010 北京文)(本小题共 13 分)
已 知 集 合 1 2 1{ | ( , , ), {0,1}, 1,2, , }( 2)n nS X X x x x x i n n …, … 对 于 1 2( , , ,)nA a a a … ,
1 2( , , ,)n nB b b b S … ,定义 A 与 B 的差为
1 1 2 2(| |,| |, | |);n nA B a b a b a b …
A 与 B 之间的距离为 1 1
1
( , ) | |
i
d A B a b
(Ⅰ)当 n=5 时,设 (0,1,0,0,1), (1,1,1,0,0)A B ,求 A B , ( , )d A B ;
(Ⅱ)证明: , , ,n nA B C S A B S 有 ,且 ( , ) ( , )d A C B C d A B ;
(Ⅲ) 证明: , , , ( , ), ( , ), ( , )nA B C S d A B d A C d B C 三个数中至少有一个是偶数
(Ⅰ)解: ( 0 1 , 1 1 , 0 1 , 0 0 , 1 0 )A B =(1,0,1,0,1)
( , ) 0 1 1 1 0 1 0 0 1 0d A B =3
(Ⅱ)证明:设 1 2 1 2 1 2( , , , ), ( , , , ), ( , , , )n n n nA a a a B b b b C c c c S
因为 1 1, {0,1}a b ,所以 1 1 {0,1}( 1,2, , )a b i n
从而 1 1 2 2( , , )n n nA B a b a b a b S
由题意知 , , {0,1}( 1,2, , )i i ia b c i n
当 0ic 时, i i i i i ia c b c a b
当 1ic 时, (1 ) (1 )i i i i i i i ia c b c a b a b
所以
1
( , ) ( , )
n
i i
i
d A C B C a b d A B
(Ⅲ)证明:设 1 2 1 2 1 2( , , , ), ( , , , ), ( , , , )n n n nA a a a B b b b C c c c S
( , ) , ( , ) , ( , )d A B k d A C l d B C h
记 0 (0,0, 0) nS 由(Ⅱ)可知
( , ) ( , ) (0, )
( , ) ( , ) (0, )
( , ) ( , )
d A B d A A B A d B A k
d A C d A A C A d C A l
d B C d B A C A h
所以 ( 1,2, , )i ib a i n 中 1 的个数为 k, ( 1,2, , )i ic a i n 中 1 的个数为l
设t 是使 1i i i ib a c a 成立的i 的个数。则 2h l k t
由此可知, , ,k l h 三个数不可能都是奇数
即 ( , ), ( , ), ( , )d A B d A C d B C 三个数中至少有一个是偶数。
71.(2010 四川理)(22)(本小题满分 14 分)
设 1
1
x
x
af ( x ) a
( 0a 且 1a ),g(x)是 f(x)的反函数.
(Ⅰ)设关于 x 的方程求 2 1 7a
tlog g( x )( x )( x )
在区间[2,6]上有实数解,求 t 的取值范围;
(Ⅱ)当 a=e(e 为自然对数的底数)时,证明:
2
2
2
2 1
n
k
n ng( k )
n( n )
;
(Ⅲ)当 0<a≤1
2
时,试比较
1
n
k
f ( k ) n
与 4 的大小,并说明理由.
本小题考产函数、反函数、方程、不等式、导数及其应用等基础知识,考察化归、分类整合等数学思想方
法,以及推理论证、分析与解决问题的能力.
解:(1)由题意,得 ax= 1
1
y
y
>0
故 g(x)= 1log 1a
x
x
,x∈(-∞,-1)∪(1,+∞)
由 2
1log log( 1)(7 ) 1a a
t x
x x x
得
t=(x-1)2(7-x),x∈[2,6]
则 t'=-3x2+18x-15=-3(x-1)(x-5)
列表如下:
x 2 (2,5) 5 (5,6) 6
t' + 0 -
t 5 ↗ 极大值 32 ↘ 25
所以 t 最小值=5,t 最大值=32
所以 t 的取值范围为[5,32]……………………………………………………5 分
(2)
2
1 2 3 1( ) ln ln ln ln3 4 5 1
n
k
ng k n
=ln( 1 2 3 1
3 4 5 1
n
n
)
=-ln ( 1)
2
n n
令 u(z)=-lnz2-
21 z
z
=-2lnz+z- 1
z
,z>0
则 u'(z)=- 2
2 11z z
=(1- 1
z )2≥0
所以 u(z)在(0,+∞)上是增函数
又因为 ( 1)
2
n n >1>0,所以 u( ( 1)
2
n n )>u(1)=0
即 ln
( 1)12 2
( 1) ( 1)
2
n n
n n n n
>0
即
2
2
2( )
2 ( 1)
n
k
n ng k
n n
………………………………………………………………9 分
(3)设 a= 1
1 p ,则 p≥1,1<f(1)=1 211
a
a p
≤3
当 n=1 时,|f(1)-1|= 2
p ≤2<4
当 n≥2 时
设 k≥2,k∈N *时,则 f(k)= (1 ) 1 21(1 ) 1 (1 ) 1
k
k k
p
p p
=1+ 1 2 2
2
k k
k k kC p C p C p
所以 1<f(k)≤1+ 1 2
2 4 4 41 1( 1) 1k kC C k k k k
从而 n-1<
2
( )
n
k
f k
≤n-1+ 4 4
2 1n
=n+1- 4
1n
<n+1
所以 n<
1
( )
n
k
f k
<f(1)+n+1≤n+4
综上所述,总有|
1
( )
n
k
f k
-n|<4
72.(2010 四川文)(22)(本小题满分 14 分)
设 1
1
x
x
af ( x ) a
( 0a 且 1a ),g(x)是 f(x)的反函数.
(Ⅰ)求 ( )g x ;
(Ⅱ)当 [2,6]x 时,恒有 2( ) log ( 1)(7 )a
tg x x x
成立,求 t 的取值范围;
(Ⅲ)当 0<a≤1
2
时,试比较 f(1)+f(2)+…+f(n)与 4n 的大小,并说明理由.
73.(2010 湖北理)(本小题满分 12 分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造
可使用 20 年的隔热层,每厘米厚的隔热层建造成本为 6 万元。该建筑物每年的能源消耗费用 C(单位:
万元)与隔热层厚度 x(单位:cm)满足关系:C(x)= (0 10),3 5
k xx
若不建隔热层,每年能源消
耗费用为 8 万元。设 f(x)为隔热层建造费用与 20 年的能源消耗费用之和。
(Ⅰ)求 k 的值及 f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用 f(x)达到最小,并求最小值。
74.(2010 福建文)(本小题满分 12 分)
某港口 O 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口 O 北偏西
30°且与该港口相距 20 海里的 A 处,并正以 30 海里/小时的航行速度沿正东方向匀速行驶。假设该小艇
沿直线方向以 海里/小时的航行速度匀速行驶,经过t 小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在 30 分钟内(含 30 分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(Ⅲ)是否存在 ,使得小艇以 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存
在,试确定 的取值范围;若不存在,请说明理由。
75.(2010 湖北文)19.(本小题满分 12 分)
已知某地今年年初拥有居民住房的总面积为 a(单位:m2),其中有部分旧住房需要拆除。当地有关部门
决定每年以当年年初住房面积的 10%建设新住房,同事也拆除面积为 b(单位:m2)的旧住房。
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了 30%,则每年拆除的旧住房面积 b
是多少?(计算时取 1.15=1.6)
76. ( 2010 湖 南
文)21.(本小题
满分 13 分)
已 知 函 数
( ) ( 1)ln 15 ,af x x a x ax
其中 a<0,且 a≠-1.
(Ⅰ)讨论函数 ( )f x 的单调性;
(Ⅱ)设函数
3 3 2( 2 3 6 4 6 ) , 1
( ), 1
( ) {
xx ax ax a a e x
e f x x
g x
(e 是自然数的底数)。是否存在 a,使 ( )g x 在[a,-a]
上为减函数?若存在,求 a 的取值范围;若不存在,请说明理由。
77.(2010 浙江理) (22)(本题满分 14 分)已知 a 是给定的实常数,设函数 2 2( ) ( ) ( )f x x a x b e ,b R ,
x a 是 ( )f x 的一个极大值点.
(Ⅰ)求b 的取值范围;
(Ⅱ)设 1 2 3, ,x x x 是 ( )f x 的 3 个极值点,问是否存在实数b ,可找到 4x R ,使得 1 2 3 4, , ,x x x x 的某种排列
1 2 3 4
, , ,i i i ix x x x (其中 1 2 3 4, , ,i i i i = 1,2,3,4 )依次成等差数列?若存在,求所有的b 及相应的 4x ;若不存在,
说明理由.
解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论
证能力、分类讨论等综合解题能力和创新意识。
(Ⅰ)解:f’(x)=ex(x-a) 2 (3 ) 2 ,x a b x b ab a
令
2
2 2
( ) (3 ) 2 ,
=(3-a+b) 4(2 ) ( 1) 8 0,
g x x a b x b ab a
b ab a a b
则
于是,假设 1 2 1 2, ( ) 0 .x x g x x x 是 的两个实根,且
当 x1=a 或 x2=a 时,则 x=a 不是 f(x)的极值点,此时不合题意。
当 x1 a 且 x2 a 时,由于 x=a 是 f(x)的极大值点,故 x10),
由已知得 x =alnx,
1
2 x = a
x
, 解德 a=
2
e ,x=e2,
两条曲线交点的坐标为(e2,e) 切线的斜率为 k=f’(e2)= 1
2e ,
切线的方程为 y-e= 1
2e (x- e2).
(2)由条件知
(Ⅰ) 当 a.>0 时,令 h ' (x)=0,解得 x= 24a ,
所以当 0 < x< 24a 时 h ' (x)<0,h(x)在(0, 24a )上递减;
当 x> 24a 时,h ' (x)>0,h(x)在(0, 24a )上递增。
所以 x> 24a 是 h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是 h(x)的最小值点。
所以Φ (a)=h( 24a )= 2a-aln 24a =2
Ⅱ当 a ≤ 0 时,h(x)=(1/2-2a) /2x>0,h(x)在(0,+∞)递增,无最小值。
故 h(x) 的最小值Φ (a)的解析式为 2a(1-ln2a) (a>o)
(3)由(2)知Φ (a)=2a(1-ln2a)
则 Φ 1(a )=-2ln2a,令Φ 1(a )=0 解得 a =1/2
当 00,所以Φ (a ) 在(0,1/2) 上递增
当 a>1/2 时, Φ 1(a )<0,所以Φ(a ) 在 (1/2, +∞)上递减。
所以Φ(a )在(0, +∞)处取得极大值Φ(1/2 )=1
因为Φ(a )在(0, +∞)上有且只有一个极致点,所以Φ(1/2)=1 也是Φ(a)的最大值
所当 a 属于 (0, +∞)时,总有Φ(a) ≤ 1
80.(2010 辽宁文)(21)(本小题满分 12 分)
已知函数 2( ) ( 1)ln 1f x a x ax .
(Ⅰ)讨论函数 ( )f x 的单调性;
(Ⅱ)设 2a ,证明:对任意 1 2, (0, )x x , 1 2 1 2| ( ) ( ) | 4 | |f x f x x x .
解:(Ⅰ) f(x)的定义域为(0,+ ),
21 2 1( ) 2a ax af x axx x
.
当 a≥0 时, ( )f x >0,故 f(x)在(0,+ )单调增加;
当 a≤-1 时, ( )f x <0, 故 f(x)在(0,+ )单调减少;
当-1<a<0 时,令 ( )f x =0,解得 x= 1
2
a
a
.当 x∈(0, 1
2
a
a
)时, ( )f x >0;
x∈( 1
2
a
a
,+ )时, ( )f x <0, 故 f(x)在(0, 1
2
a
a
)单调增加,在( 1
2
a
a
,+ )单调减少.
(Ⅱ)不妨假设 x1≥x2.由于 a≤-2,故 f(x)在(0,+ )单调减少.
所以 1 2 1 2( ) ( ) 4f x f x x x 等价于
1 2( ) ( )f x f x ≥4x1-4x2,
即 f(x2)+ 4x2≥f(x1)+ 4x1.
令 g(x)=f(x)+4x,则
1( ) 2ag x axx
+4
=
22 4 1ax x a
x
.
于是 ( )g x ≤
24 4 1x x
x
=
2(2 1)x
x
≤0.
从而 g(x)在(0,+ )单调减少,故 g(x1) ≤g(x2),
即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意 x1,x2∈(0,+ ) , 1 2 1 2( ) ( ) 4f x f x x x .
81.(2010 辽宁理)(21)(本小题满分 12 分)
已知函数 1ln)1()( 2 axxaxf
(I)讨论函数 )(xf 的单调性;
(II)设 1a .如果对任意 ),0(, 21 xx , ||4)()(| 2121 xxxfxf ,求 a 的取值范围。
解:
(Ⅰ) ( )f x 的定义域为(0,+∞).
21 2 1'( ) 2a ax af x axx x
.
当 0a 时, '( )f x >0,故 ( )f x 在(0,+∞)单调增加;
当 1a 时, '( )f x <0,故 ( )f x 在(0,+∞)单调减少;
当-1< a <0 时,令 '( )f x =0,解得 1
2
ax a
.
则当 1(0, )2
ax a
时, '( )f x >0; 1( , )2
ax a
时, '( )f x <0.
故 ( )f x 在 1(0, )2
a
a
单调增加,在 1( , )2
a
a
单调减少.
(Ⅱ)不妨假设 1 2x x ,而 a <-1,由(Ⅰ)知在(0,+∞)单调减少,从而
1 2, (0, )x x , 1 2 1 2( ) ( ) 4f x f x x x
等价于
1 2, (0, )x x , 2 2 1 1( ) 4 ( ) 4f x x f x x ①
令 ( ) ( ) 4g x f x x ,则 1'( ) 2 4ag x axx
①等价于 ( )g x 在(0,+∞)单调减少,即
1 2 4 0a axx
.
从而
2 2 2
2 2 2
4 1 (2 1) 4 2 (2 1) 22 1 2 1 2 1
x x x xa x x x
故 a 的取值范围为(-∞,-2]. ……12 分
82.(2010 全国卷 2 文)(21)(本小题满分 12 分)
已知函数 f(x)=x 3 -3ax 2 +3x+1。
(Ⅰ)设 a=2,求 f(x)的单调期间;
(Ⅱ)设 f(x)在区间(2,3)中至少有一个极值点,求 a 的取值范围。
【解析】本题考查了导数在函数性质中的应用,主要考查了用导数研究函数的单调区间、极值及函数与方
程的知识。
(1)求出函数的导数,由导数大于 0,可求得增区间,由导数小于 0,可求得减区间。
(2)求出函数的导数 ( )f x ,在(2,3)内有极值,即为 ( )f x 在(2,3)内有一个零点,即可根据
(2) (3) 0f f ,即可求出 a 的取值范围。
83.(2010 江西理)19. (本小题满分 12 分)
设函数 ln ln 2 ( 0)f x x x ax a 。
(1)当 a=1 时,求 f x 的单调区间。
(2)若 f x 在 01, 上的最大值为 1
2
,求 a 的值。
【解析】考查函数导数运算、利用导数处理函数最值等知识。
解:对函数求导得: 1 1( ) 2f x ax x
,定义域为(0,2)
单调性的处理,通过导数的零点进行穿线判别符号完成。
当 a=1 时,令
21 1 2( ) 0 +1=0 02 2
xf x x x x x
得 ( )
当 (0, 2), ( ) 0,x f x 为增区间;当 ( 2 2), ( ) 0,x f x , 为减函数。
区间 01, 上的最值问题,通过导数得到单调性,结合极值点和端点的比较得到,确定
待定量 a 的值。
当 01x ,有最大值,则必不为减函数,且 1 1( ) 2f x ax x
>0,为单调递增区间。
最大值在右端点取到。 max
1(1) 2f f a 。
84.(2010 安徽文)20.(本小题满分 12 分)
设函数 sin cos 1f x x x x , 0 2x ,求函数 f x 的单调区间与极值。
【命题意图】本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合应用数学知识解
决问题的能力.
【解题指导】(1)对函数 sin cos 1f x x x x 求导,对导函数用辅助角公式变形,利用导数等于 0
得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值.
,
,
,
( ) 1 2 ( ).4
2 3( ) 0 ( )4 2 2
( )
x x
x x x x
x x
解:由f(x)=sinx-cosx+x+1,00.
(Ⅰ)若 a=1,求曲线 y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间 1 1,2 2
上,f(x)>0 恒成立,求 a 的取值范围.
【解析】本小题主要考查曲线的切线方程、利用导数研究函数的单调性与极值、解不等式等基础知识,考
查运算能力及分类讨论的思想方法.满分 12 分.
(Ⅰ)解:当 a=1 时,f(x)= 3 23x x 12
,f(2)=3;f’(x)= 23 3x x , f’(2)=6.所以曲线 y=f(x)在点
(2,f(2))处的切线方程为 y-3=6(x-2),即 y=6x-9.
(Ⅱ)解:f’(x)= 23 3 3 ( 1)ax x x ax .令 f’(x)=0,解得 x=0 或 x= 1
a .
以下分两种情况讨论:
若 1 10 a 2 a 2
,则 ,当 x 变化时,f’(x),f(x)的变化情况如下表:
X 1 02
, 0 1
2
0,
f’(x) + 0 -
f(x) 极大值
当 1 1x f x2 2
, 时, ( )>0 等价于
5 a1 0,( ) 0, 82
1 5 a( ) 0, 0.2 8
f
f
即
解不等式组得-52,则 1 10 a 2
.当 x 变化时,f’(x),f(x)的变化情况如下表:
X 1 02
, 0 1
a
0, 1
a
1 1
a 2
,
f’(x) + 0 - 0 +
f(x) 极大值 极小值
当 1 1x 2 2
, 时,f(x)>0 等价于
1f(- )2
1f( )>0,a
>0,
即
2
5
8
11- >0.2
a
a
>0,
解不等式组得 2 52 a 或 2
2a .因此 21 时,2x-2>0,从而 2x-2e 1 0, 0, Fxe 又 所以 ’(x)>0,从而函数 F(x)在[1,+∞)是增函数。
又 F(1)= -1 -1e e 0 ,所以x>1时,有F(x)>F(1)=0,即 f(x)>g(x).
(Ⅲ)证明:(1)
若 1 2 1 2 1 2( 1)( 1) 0, ) ), 1.x x x x x x 1 2由( )及f(x f(x 则 与 矛盾。
(2)若 1 2 1 2 1 2( 1)( 1) 0, ) ), .x x x x x x 1 2由( )及f(x f(x 得 与 矛盾。
根据(1)(2)得 1 2 1 2( 1)( 1) 0, 1, 1.x x x x 不妨设
由(Ⅱ)可知, )2f(x > )2g(x ,则 )2g(x = )2f(2-x ,所以 )2f(x > )2f(2-x ,从而 )1f(x > )2f(2-x .因为 2 1x ,
所以 22 1x ,又由(Ⅰ)可知函数 f(x)在区间(-∞,1)内事增函数,所以 1x > 22 x ,即 1 2x x >2.
92.(2010 福建文)22.(本小题满分 14 分)
已知函数 f(x)= 3 21
3 x x ax b 的图像在点 P(0,f(0))处的切线方程为 y=3x-2
(Ⅰ)求实数 a,b 的值;
(Ⅱ)设 g(x)=f(x)+
1
m
x
是[ 2, ]上的增函数。
(i)求实数 m 的最大值;
(ii)当 m 取最大值时,是否存在点 Q,使得过点 Q 的直线若能与曲线 y=g(x)围成两个封闭图形,则这两
个封闭图形的面积总相等?若存在,求出点 Q 的坐标;若不存在,说明理由。
93.(2010 全国卷 1 理)(20)(本小题满分 12 分)
已知函数 ( ) ( 1)ln 1f x x x x .
(Ⅰ)若 2'( ) 1xf x x ax ,求 a 的取值范围;
(Ⅱ)证明: ( 1) ( ) 0x f x .
94.(2010 湖北文)21.(本小题满分 14 分)
设函数 3 21 ax x bx c3 2f (x)= ,其中 a>0,曲线 xy f ( )在点 P(0, 0f( ))处的切线方程为 y=1
(Ⅰ)确定 b、c 的值
(Ⅱ)设曲线 xy f ( )在点( 1 1x xf,( ))及( 2 2x xf,( ))处的切线都过点(0,2)证明:当 1 2x x 时,
1 2'( ) '( )f x f x
(Ⅲ)若过点(0,2)可作曲线 xy f ( )的三条不同切线,求 a 的取值范围。
95.(2010 湖南理)20.(本小题满分 13 分)
已知函数 2( ) ( , ),f x x bx c b c R 对任意的 x R ,恒有 ' ( )f x ( )f x 。
(Ⅰ)证明:当 0x 时, 2( ) ( )f x x c ;
(Ⅱ)若对满足题设条件的任意 b,c,不等式 2 2( ) ( ) ( )f c f b M c b 恒成立,求 M 的最小值。
解析:
96.(2010 福建理)20.(本小题满分 14 分)
(Ⅰ)已知函数 3(x)=x -xf ,其图象记为曲线C 。
(i)求函数 (x)f 的单调区间;
(ii)证明:若对于任意非零实数 1x ,曲线 C 与其在点 1 1 1P (x ,f(x )) 处的切线交于另一点
2 2 2P (x ,f(x )) ,曲线 C 与其在点 2 2 2P (x ,f(x )) 处的切线交于另一点 3 3 3P (x ,f(x )) ,线段
1
1 2 2 3 1 2
2
P P ,P P ,S , SC S
与曲线 所围成封闭图形的面积分别记为S 则 为定值;
(Ⅱ)对于一般的三次函数 3 2g(x)=ax +bx +cx+d(a 0), 请给出类似于 (Ⅰ)(ii)的正确命题,并予以
证明。
【命题意图】本小题主要考查函数、导数、定积分等基础知识,考查抽象概括能力、运算求解能力、推理
论证能力,考查函数与方程思想、数形结合思想、化归与转化思想、特殊与一般思想。
【解析】(Ⅰ)(i)由 3(x)=x -xf 得 ' 2(x)=3x -1f = 3 33(x- )(x+ )3 3
,
当 3x (- ,- )3
和 3
3
( , )时, ' (x)>0f ;
当 3x (- ,3
3 )3
时, ' (x)<0f ,
因此, (x)f 的单调递增区间为 3(- ,- )3
和 3
3
( , ),单调递减区间为 3(- ,3
3 )3
。
97.(2010 湖北理数)
98.(2010 安徽理)17、(本小题满分 12 分)
设 a 为实数,函数 2 2 ,xf x e x a x R 。
(Ⅰ)求 f x 的单调区间与极值;
(Ⅱ)求证:当 ln 2 1a 且 0x 时, 2 2 1xe x ax 。
99.(2010 江苏卷)20、(本小题满分 16 分)
设 )(xf 是定义在区间 ),1( 上的函数,其导函数为 )(' xf 。如果存在实数 a 和函数 )(xh ,其中 )(xh 对任
意的 ),1( x 都有 )(xh >0,使得 )1)(()(' 2 axxxhxf ,则称函数 )(xf 具有性质 )(aP 。
(1)设函数 )(xf 2ln ( 1)1
bx xx
,其中b 为实数。
(i)求证:函数 )(xf 具有性质 )(bP ; (ii)求函数 )(xf 的单调区间。
(2)已知函数 )(xg 具有性质 )2(P 。给定 1 2 1 2, (1, ), ,x x x x 设 m 为实数,
21 )1( xmmx , 21)1( mxxm ,且 1,1 ,
若| )()( gg |<| )()( 21 xgxg |,求 m 的取值范围。
【解析】 本小题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用数形结合、分类讨
论的思想方法进行探索、分析与解决问题的综合能力。满分 16 分。
(1)(i) '( )f x 2
2 2
1 2 1 ( 1)( 1) ( 1)
b x bxx x x x
∵ 1x 时, 2
1( ) 0( 1)h x x x
恒成立,
∴函数 )(xf 具有性质 )(bP ;
(ii)(方法一)设
2
2 2( ) 1 ( ) 12 4
b bx x bx x , ( )x 与 )(' xf 的符号相同。
当
2
1 0, 2 24
b b 时, ( )x 0 , )(' xf 0 ,故此时 )(xf 在区间 ),1( 上递增;
当 2b 时,对于 1x ,有 )(' xf 0 ,所以此时 )(xf 在区间 ),1( 上递增;
当 2b 时, ( )x 图像开口向上,对称轴 12
bx ,而 (0) 1 ,
对于 1x ,总有 ( )x 0 , )(' xf 0 ,故此时 )(xf 在区间 ),1( 上递增;
(方法二)当 2b 时,对于 1x , 2 2 2( ) 1 2 1 ( 1) 0x x bx x x x
所以 )(' xf 0 ,故此时 )(xf 在区间 ),1( 上递增;
当 2b 时, ( )x 图像开口向上,对称轴 12
bx ,方程 ( ) 0x 的两根为:
2 24 4,2 2
b b b b ,
而
2 2
2
4 4 21, (0,1)2 2 4
b b b b
b b
当
2 4(1, )2
b bx 时, ( )x 0 , )(' xf 0 ,故此时 )(xf 在区间
2 4(1, )2
b b 上递减;
同理得: )(xf 在区间
2 4[ , )2
b b 上递增。
综上所述,当 2b 时, )(xf 在区间 ),1( 上递增;
当 2b 时, )(xf 在 2 4(1, )2
b b 上递减; )(xf 在
2 4[ , )2
b b 上递增。
(2)(方法一)由题意,得: 2 2'( ) ( )( 2 1) ( )( 1)g x h x x x h x x
又 )(xh 对任意的 ),1( x 都有 )(xh >0,
所以对任意的 ),1( x 都有 ( ) 0g x , ( )g x 在 (1, ) 上递增。
又 1 2 1 2, (2 1)( )x x m x x 。
当 1 , 12m m 时, ,且 1 1 2 2 1 2( 1) (1 ) , (1 ) ( 1)x m x m x x m x m x ,
综合以上讨论,得:所求 m 的取值范围是(0,1)。
(方法二)由题设知, ( )g x 的导函数 2'( ) ( )( 2 1)g x h x x x ,其中函数 ( ) 0h x 对于任意的 ),1( x
都成立。所以,当 1x 时, 2'( ) ( )( 1) 0g x h x x ,从而 ( )g x 在区间 ),1( 上单调递增。
①当 (0,1)m 时,有 1 2 1 1 1(1 ) (1 )mx m x mx m x x ,
1 2 2 2 2(1 ) (1 )mx m x mx m x x ,得 1 2( , )x x ,同理可得 1 2( , )x x ,所以由 ( )g x 的单调
性知 ( )g 、 ( )g 1 2( ( ), ( ))g x g x ,
从而有| )()( gg |<| )()( 21 xgxg |,符合题设。
②当 0m 时, 1 2 2 2 2(1 ) (1 )mx m x mx m x x ,
1 2 1 1 1(1 ) (1 )m x mx m x mx x , 于 是 由 1, 1 及 ( )g x 的 单 调 性 知
1 2( ) ( ) ( ) ( )g g x g x g ,所以| )()( gg |≥| )()( 21 xgxg |,与题设不符。
③当 1m 时,同理可得 1 2,x x ,进而得| )()( gg |≥| )()( 21 xgxg |,与题设不符。
因此综合①、②、③得所求的 m 的取值范围是(0,1)。
2009 年高考题
1.(2009 全国卷Ⅰ理)函数 ( )f x 的定义域为 R,若 ( 1)f x 与 ( 1)f x 都是奇函数,则( )
A. ( )f x 是偶函数 B. ( )f x 是奇函数
C. ( ) ( 2)f x f x D. ( 3)f x 是奇函数
答案 D
解析 ( 1)f x 与 ( 1)f x 都是奇函数,
( 1) ( 1), ( 1) ( 1)f x f x f x f x ,
函 数 ( )f x 关 于 点 (1,0) , 及 点 ( 1,0) 对 称 , 函 数 ( )f x 是 周 期 2[1 ( 1)] 4T 的 周 期 函
数. ( 1 4) ( 1 4)f x f x , ( 3) ( 3)f x f x ,即 ( 3)f x 是奇函数。故选 D
2.(2009 浙江理)对于正实数 ,记 M 为满足下述条件的函数 ( )f x 构成的集合: 1 2,x x R 且 2 1x x ,
有 2 1 2 1 2 1( ) ( ) ( ) ( )x x f x f x x x .下列结论中正确的是 ( )
A.若 1( )f x M , 2( )g x M ,则 1 2( ) ( )f x g x M
B.若 1( )f x M , 2( )g x M ,且 ( ) 0g x ,则 1
2
( )
( )
f x Mg x
C.若 1( )f x M , 2( )g x M ,则 1 2( ) ( )f x g x M
D.若 1( )f x M , 2( )g x M ,且 1 2 ,则 1 2( ) ( )f x g x M
答案 C
解 析 对 于 2 1 2 1 2 1( ) ( ) ( ) ( )x x f x f x x x , 即 有 2 1
2 1
( ) ( )f x f x
x x
, 令
2 1
2 1
( ) ( )f x f x kx x
, 有 k , 不 妨 设 1( )f x M , 2( )g x M , 即 有
1 1 ,fk 2 2gk ,因此有 1 2 1 2f gk k ,因此有 1 2( ) ( )f x g x M .
3.(2009 浙江文)若函数 2( ) ( )af x x ax
R ,则下列结论正确的是( )
A. a R , ( )f x 在 (0, ) 上是增函数
B. a R , ( )f x 在 (0, ) 上是减函数
C. a R , ( )f x 是偶函数
D. a R , ( )f x 是奇函数
答案 C
【命题意图】此题主要考查了全称量词与存在量词的概念和基础知识,通过对量词的考查结合函数的性
质进行了交汇设问.
解析 对于 0a 时有 2f x x 是一个偶函数
4. (2009 山东卷理)函数
x x
x x
e ey e e
的图像大致为 ( ).
答案 A
解 析 函 数 有 意 义 , 需 使 0x xe e , 其 定 义 域 为 0| xx , 排 除 C,D, 又 因 为
2
2 2
1 211 1
x x x
x x x x
e e ey e e e e
,所以当 0x 时函数为减函数,故选 A.
【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函
数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
5.(2009 山东卷理)定义在 R 上的函数 f(x)满足 f(x)=
0),2()1(
0),1(log 2
xxfxf
xx ,
则 f(2009)的值为 ( )
A.-1 B. 0 C.1 D. 2
答案 C
解析 由已知得 2( 1) log 2 1f , (0) 0f , (1) (0) ( 1) 1f f f ,
(2) (1) (0) 1f f f , (3) (2) (1) 1 ( 1) 0f f f ,
(4) (3) (2) 0 ( 1) 1f f f , (5) (4) (3) 1f f f , (6) (5) (4) 0f f f ,
所以函数 f(x)的值以 6 为周期重复性出现.,所以 f(2009)= f(5)=1,故选 C.
【命题立意】:本题考查归纳推理以及函数的周期性和对数的运算.
6.(2009 山东卷文)函数
x x
x x
e ey e e
的图像大致为( ).
1
x
y
1O
A
x
y
O
1
1
B
x
y
O 1
1
C
x
y
1
1
D
O
答案 A.
解 析 函 数 有 意 义 , 需 使 0x xe e , 其 定 义 域 为 0| xx , 排 除 C,D, 又 因 为
2
2 2
1 211 1
x x x
x x x x
e e ey e e e e
,所以当 0x 时函数为减函数,故选 A.
【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函
数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
7. (2009 山东卷文)定义在 R 上的函数 f(x)满足 f(x)=
0),2()1(
0),4(log 2
xxfxf
xx ,
则 f(3)的值为 ( )
A.-1 B. -2 C.1 D. 2
答案 B
解析 由已知得 2( 1) log 5f , 2(0) log 4 2f , 2(1) (0) ( 1) 2 log 5f f f ,
2(2) (1) (0) log 5f f f , 2 2(3) (2) (1) log 5 (2 log 5) 2f f f ,故选 B.
【命题立意】:本题考查对数函数的运算以及推理过程.
8.(2009 山东卷文)已知定义在 R 上的奇函数 )(xf ,满足 ( 4) ( )f x f x ,且在区间[0,2]上是增函数,则
( ).
A. ( 25) (11) (80)f f f B. (80) (11) ( 25)f f f
C. (11) (80) ( 25)f f f D. ( 25) (80) (11)f f f
答案 D
解析 因为 )(xf 满足 ( 4) ( )f x f x ,所以 ( 8) ( )f x f x ,所以函数是以 8 为周期的周期函数, 则
)1()25( ff , )0()80( ff , )3()11( ff , 又 因 为 )(xf 在 R 上 是 奇 函 数 , (0) 0f , 得
0)0()80( ff , )1()1()25( fff , 而 由 ( 4) ( )f x f x 得
)1()41()3()3()11( fffff ,又因为 )(xf 在区间[0,2]上是增函数,所以 0)0()1( ff ,
1
x
y
1O
A
x
y
O
1
1
B
x
y
O 1
1
C
x
y
1
1
D
O
所以 0)1( f ,即 ( 25) (80) (11)f f f ,故选 D.
【命题立意】:本题综合考查了函数的奇偶性、单调性、周期性等性质,运用化归的数学思想和数形结合的
思想解答问题.
9.(2009 全国卷Ⅱ文)函数 y= x (x 0)的反函数是 ( )
(A) 2y x (x 0) (B) 2y x (x 0)
(B) 2y x (x0) (D) 2y x (x0)
答案 B
解析 本题考查反函数概念及求法,由原函数 x 0 可知 AC 错,原函数 y 0 可知 D 错.
10.(2009 全国卷Ⅱ文)函数 y= 2
2log 2
xy x
的图像 ( )
(A) 关于原点对称 (B)关于主线 y x 对称
(C) 关于 y 轴对称 (D)关于直线 y x 对称
答案 A
解析 本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又 f(-x)=-f(x),故函数为奇
函数,图像关于原点对称,选 A。
11.(2009 全国卷Ⅱ文)设 2lg , (lg ) , lg ,a e b e c e 则 ( )
(A) a b c (B) a c b (C) c a b (D) c b a
答案 B
解析 本题考查对数函数的增减性,由 1>lge>0,知 a>b,又 c=
2
1 lge, 作商比较知 c>b,选 B。
12.(2009 广东卷理)若函数 ( )y f x 是函数 ( 0, 1)xy a a a 且 的反函数,其图像经过点 ( , )a a ,
则 ( )f x ( )
A. 2log x B. 1
2
log x C. 1
2x D. 2x
答案 B
解析 xxf alog)( ,代入 ( , )a a ,解得
2
1a ,所以 ( )f x 1
2
log x ,选 B.
13.(2009 广东卷理)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙
车的速度曲线分别为 v v乙甲和 (如图 2 所示).那么对于图中给定的 0 1t t和 ,下列判断中一定正确的是
( )
A. 在 1t 时刻,甲车在乙车前面
B. 1t 时刻后,甲车在乙车后面
C. 在 0t 时刻,两车的位置相同
D. 0t 时刻后,乙车在甲车前面
答案 A
解析 由图像可知,曲线 甲v 比 乙v 在 0~ 0t 、0~ 1t 与 x 轴所围成图形面积大,则在 0t 、 1t 时刻,甲车均在
乙车前面,选 A.
14.(2009 安徽卷理)设 a <b,函数 2( ) ( )y x a x b 的图像可能是 ( )
答案 C
解析 / ( )(3 2 )y x a x a b ,由 / 0y 得 2, 3
a bx a x ,∴当 x a 时, y 取极大值 0,当
2
3
a bx 时 y 取极小值且极小值为负。故选 C。
或当 x b 时 0y ,当 x b 时, 0y 选 C
15.(2009 安徽卷文)设 ,函数 的图像可能是 ( )
答案 C
解析 可得 2, ( ) ( ) 0x a x b y x a x b 为 的两个零解.
当 x a 时,则 ( ) 0x b f x
当 a x b 时,则 ( ) 0,f x 当 x b 时,则 ( ) 0.f x 选 C。
16.(2009 江西卷文)函数
2 3 4x xy x
的定义域为 ( )
A.[ 4,1] B.[ 4, 0) C. (0,1] D.[ 4, 0) (0,1]
答案 D
解析 由 2
0
3 4 0
x
x x
得 4 0x 或 0 1x ,故选 D.
17.(2009 江西卷文)已知函数 ( )f x 是 ( , ) 上的偶函数,若对于 0x ,都有 ( 2 ( )f x f x ) ,且
当 [0,2)x 时, 2( ) log ( 1f x x ),则 ( 2008) (2009)f f 的值为
( )
A. 2 B. 1 C.1 D. 2
答案 C
解析 1 2
2 2( 2008) (2009) (0) (1) log log 1f f f f ,故选 C.
18.(2009 江西卷文)如图所示,一质点 ( , )P x y 在 xOy 平面上沿曲线运动,
速度大小不 变,其在 x 轴上的投影点 ( ,0)Q x 的运动速度 ( )V V t 的图象
大致为 ( )
A B C D
答案 B
解析 由图可知,当质点 ( , )P x y 在两个封闭曲线上运动时,投影点 ( ,0)Q x 的速度先由正到 0、到负数,
再到 0,到正,故 A 错误;质点 ( , )P x y 在终点的速度是由大到小接近 0,故 D 错误;质点 ( , )P x y 在开始
时沿直线运动,故投影点 ( ,0)Q x 的速度为常数,因此C 是错误的,故选 B .
19.(2009 江西卷理)函数 2
ln( 1)
3 4
xy
x x
的定义域为 ( )
A. ( 4, 1) B. ( 4,1) C. ( 1,1) D. ( 1,1]
答案 C
解析 由 2
1 0 1 1 14 13 4 0
x x xxx x
.故选 C
20.(2009 江西卷理)设函数 2( ) ( 0)f x ax bx c a 的定义域为 D ,若所有点 ( , ( ))( , )s f t s t D 构
O
( )V t
t O
( )V t
t
t
O
( )V t
t
y
xO
( , )P x y
( ,0)Q x
成一个正方形区域,则 a 的值为 ( )
A. 2 B. 4 C. 8 D.不能确定
答案 B
解析 1 2 max| | ( )x x f x ,
2 2
2
4 4
4
b ac ac b
a a
,| | 2a a , 4a ,选 B
21.(2009 天津卷文)设函数
0,6
0,64)(
2
xx
xxxxf 则不等式 )1()( fxf 的解集是( )
A. ),3()1,3( B. ),2()1,3(
C. ),3()1,1( D. )3,1()3,(
答案 A
解析 由已知,函数先增后减再增
当 0x , 2)( xf 3)1( f 令 ,3)( xf
解得 3,1 xx 。
当 0x , 3,36 xx
故 3)1()( fxf ,解得 313 xx 或
【考点定位】本试题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
22.(2009 天津卷文)设函数 f(x)在 R 上的导函数为 f’(x),且 2f(x)+xf’(x)>x 2 ,x 下面的不等式在 R 内恒成立
的是 ( )
A. 0)( xf B. 0)( xf C. xxf )( D. xxf )(
答案 A
解析 由已知,首先令 0x ,排除 B,D。然后结合已知条件排除 C,得到 A
【考点定位】本试题考察了导数来解决函数单调性的运用。通过分析解析式的特点,考查了分析问题和解
决问题的能力。
23.(2009 湖北卷理)设 a 为非零实数,函数 1 1( , )1
axy x R xax a
且 的反函数是 ( )
A、 1 1( , )1
axy x R xax a
且 B、 1 1( , )1
axy x R xax a
且
C、 1 ( , 1)(1 )
xy x R xa x
且 D、 1 ( , 1)(1 )
xy x R xa x
且
答案 D
解析 由原函数是 1 1( , )1
axy x R xax a
且 ,从中解得
1 ( , 1)(1 )
yx y R ya y
且 即原函数的反函数是 1 ( , 1)(1 )
yx y R ya y
且 ,故选择 D
24..(2009 湖北卷理)设球的半径为时间 t 的函数 R t 。若球的体积以均匀速度 c 增长,则球的表面积的增
长速度与球半径 ( )
A.成正比,比例系数为 C B. 成正比,比例系数为 2C
C.成反比,比例系数为 C D. 成反比,比例系数为 2C
答案 D
解析 由题意可知球的体积为 34( ) ( )3V t R t ,则 ' 2 '( ) 4 ( ) ( )c V t R t R t ,由此可
' 4 ( )( ) ( )
c R tR t R t
,而球的表面积为 2( ) 4 ( )S t R t ,
所以 ' 2 '( ) 4 ( ) 8 ( ) ( )v S t R t R t R t 表= ,
【3 年高考 2 年模拟】第二章函数与导数(续)
即 ' ' '
'
2 28 ( ) ( ) 2 4 ( ) ( ) ( )( ) ( ) ( )
c cv R t R t R t R t R tR t R t R t
表= = = = ,故选
25.(2009 四川卷文)已知函数 )(xf 是定义在实数集 R 上的不恒为零的偶函数,且对任意实数 x 都有
)()1()1( xfxxxf ,则 )2
5(f 的值是 ( )
A. 0 B.
2
1 C. 1 D.
2
5
答案 A
解析 若 x ≠0,则有 )(1)1( xfx
xxf ,取
2
1x ,则有:
)2
1()2
1()2
1(
2
1
2
11
)12
1()2
1( fffff
(∵ )(xf 是偶函数,则
)2
1()2
1( ff )由此得 0)2
1( f 于是
0)2
1(5)2
1(]
2
1
2
11
[3
5)12
1(3
5)2
3(3
5)2
3(
2
3
2
31
)12
3()2
5(
fffffff
26.(2009 福建卷理)函数 ( ) ( 0)f x ax bx c a 的图象关于直线
2
bx a
对称。据此可推测,对任意
的非零实数 a,b,c,m,n,p,关于 x 的方程 2( ) ( ) 0m f x nf x p 的解集都不可能是
( )
A. 1,2 B 1,4 C 1,2,3,4 D 1,4,16,64
( ) 2 4( 2)y f x x x
答案 D
解析 本题用特例法解决简洁快速,对方程 2[ ( )] ( ) 0m f x nf x P 中 , ,m n p 分别赋值求出 ( )f x 代入
( ) 0f x 求出检验即得.
27.(2009 辽宁卷文)已知偶函数 ( )f x 在区间0, ) 单调增加,则满足 (2 1)f x < 1( )3f 的 x 取值范围
是 ( )
(A)( 1
3
, 2
3
) B.[ 1
3
, 2
3
) C.( 1
2
, 2
3
) D.[ 1
2
, 2
3
)
答案 A
解析 由于 f(x)是偶函数,故 f(x)=f(|x|)
∴得 f(|2x-1|)<f( 1
3 ),再根据 f(x)的单调性
得|2x-1|< 1
3
解得 1
3
<x< 2
3
28.(2009 宁夏海南卷理)用 min{a,b,c}表示 a,b,c 三个数中的最小值 ( )
设 f(x)=min{, x+2,10-x} (x 0),则 f(x)的最大值为
(A)4 (B)5 (C)6 (D)7
答案 C
29.(2009 陕西卷文)函数 ( ) 2 4( 4)f x x x 的反函数为 ( )
(A) 1 21( ) 4( 0)2f x x x B. 1 21( ) 4( 2)2f x x x
(C) 1 21( ) 2( 0)2f x x x (D)学科 1 21( ) 2( 2)2f x x x
答案 D
解析 令原式 则
故 1 21( ) 2( 2)2f x x x 故选 D.
30. ( 2009 陕 西 卷 文 ) 定 义 在 R 上 的 偶 函 数 ( )f x 满 足 : 对 任 意 的 1 2 1 2, [0, )( )x x x x , 有
2 1
2 1
( ) ( ) 0f x f x
x x
.则 ( )
(A) (3) ( 2) (1)f f f B. (1) ( 2) (3)f f f
C. ( 2) (1) (3)f f f D. (3) (1) ( 2)f f f
答案 A
解析 由 2 1 2 1( )( ( ) ( )) 0x x f x f x 等价,于 2 1
2 1
( ) ( ) 0f x f x
x x
则 ( )f x 在
2 2
2 42 4, 22 2
y yy x x 即
1 2 1 2, ( ,0]( )x x x x 上单调递增, 又 ( )f x 是偶函数,故 ( )f x 在
1 2 1 2, (0, ]( )x x x x 单调递减.且满足 *n N 时, ( 2) (2)f f , 03>2 1 ,得
(3) ( 2) (1)f f f ,故选 A.
31.(2009 陕西卷理)定义在 R 上的偶函数 ( )f x 满足:对任意
的 1 2 1 2, ( ,0]( )x x x x ,有 2 1 2 1( )( ( ) ( )) 0x x f x f x .
则当 *n N 时,有 ( )
(A) ( ) ( 1) ( 1)f n f n f n B. ( 1) ( ) ( 1)f n f n f n
C. C. ( 1) ( ) ( 1)f n f n f n D. ( 1) ( 1) ( )f n f n f n
答案 C
32.(2009 四川卷文)已知函数 )(xf 是定义在实数集 R 上的不恒为零的偶函数,且对任意实数 x 都有
)()1()1( xfxxxf ,则 )2
5(f 的值是 ( )
A. 0 B.
2
1 C. 1 D.
2
5
答案 A
解析 若 x ≠0,则有 )(1)1( xfx
xxf ,取
2
1x ,则有:
)2
1()2
1()2
1(
2
1
2
11
)12
1()2
1( fffff
(∵ )(xf 是偶函数,则 )2
1()2
1( ff )
由此得 0)2
1( f 于是,
0)2
1(5)2
1(]
2
1
2
11
[3
5)12
1(3
5)2
3(3
5)2
3(
2
3
2
31
)12
3()2
5(
fffffff
33.(2009 湖北卷文)函数 )2
1,(21
21
xRxx
xy 且 的反函数是 ( )
1 2 1 2 2 1 2 1
2 1 2 1
, ( ,0]( ) ( )( ( ) ( )) 0
( ) ( ) ( ) ( ,0]
( ) ( ) (0 ]
( 1) ( ) ( 1) ( 1) ( ) ( 1)
x x x x x x f x f x
x x f x f x f x
f x f x
f n f n f n f n f n f n
解析:
时, 在 为增函数
为偶函数 在 , 为减函数
而n+1>n>n-1>0,
A. )2
1,(21
21
xRxx
xy 且 B. )2
1,(21
21
xRxx
xy 且
C. )1,()1(2
1
xRxx
xy 且 D. )1,()1(2
1
xRxx
xy 且
答案 D
解析 可反解得 11 1( )2(1 ) 2(1 )
y xx f xy x
故 且可得原函数中 y∈R、y≠-1 所以 1 1( ) 2(1 )
xf x x
且 x
∈R、x≠-1 选 D
34.(2009 湖南卷理)如图 1,当参数 2 时,连续函数 ( 0)1
xy xx
的图像分别对应曲线 1C 和 2C ,
则 ( )
A 10 B 10
C 1 2 0 D 2 1 0
答案 B
解析 解析由条件中的函数是分式无理型函数,先由函
数在 (0, ) 是连续的,可知参数 1 20, 0 ,即排除 C, D项,又取 1x ,
知对应函数值 1 2
1 2
1 1,
1 1
y y
,由图可知 1 2 ,y y 所以 1 2 ,即选 B 项。
35.(2009 湖南卷理)设函数 ( )y f x 在( ,+ )内有定义。对于给定的正数 K,定义函数
( )
( ), ( )( ) , ( )k
f x f x Kf x K f x K
取函数 ( )f x = 12 x e 。若对任意的 ( , )x ,恒有 ( )kf x = ( )f x ,则 ( )
A.K 的最大值为 2 B. K 的最小值为 2
C.K 的最大值为 1 D. K 的最小值为 1
答案 D
解析 由 '( ) 1 0,xf x e 知 0x ,所以 ( ,0)x 时, '( ) 0f x ,当 (0, )x 时, '( ) 0f x ,
所以 max( ) (0) 1,f x f 即 ( )f x 的值域是 ( ,1] ,而要使 ( ) ( )kf x f x 在 R 上恒成立,结合条件分别取
不同的 K 值,可得 D 符合,此时 ( ) ( )kf x f x 。故选 D 项。
36.(2009 天津卷理)已知函数
0,4
0,4)( 2
2
xxx
xxxxf 若 2(2 ) ( ),f a f a 则实数 a
的取值范围是 ( )
A ( , 1) (2, ) B ( 1,2) C ( 2,1) D ( , 2) (1, )
【考点定位】本小题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
解析:由题知 )(xf 在 R 上是增函数,由题得 aa 22 ,解得 12 a ,故选择 C。
37.(2009 四川卷理)已知函数 ( )f x 是定义在实数集 R 上的不恒为零的偶函数,且对任意实数 x 都有
( 1) (1 ) ( )xf x x f x ,则 5( ( ))2f f 的值是 ( )
A.0 B. 1
2 C.1 D. 5
2
【考点定位】本小题考查求抽象函数的函数值之赋值法,综合题。(同文 12)
答案 A
解析 令
2
1x ,则 0)2
1()2
1(2
1)2
1(2
1)2
1(2
1 ffff ;令 0x ,则 0)0( f
由 ( 1) (1 ) ( )xf x x f x 得 )(1)1( xfx
xxf ,所以
0)0())2
5((0)2
1(
2
1
2
3
3
5)2
3(3
5)2
3(
2
3
2
5
)2
5( fffffff ,故选择 A。
38.(2009 福建卷文)下列函数中,与函数 1y
x
有相同定义域的是 ( )
A . ( ) lnf x x B. 1( )f x x
C. ( ) | |f x x D. ( ) xf x e
答案 A
解析 解析 由 1y
x
可得定义域是 0. ( ) lnx f x x 的定义域 0x ; 1( )f x x
的定义域是 x ≠0;
( ) | |f x x 的定义域是 ; ( ) xx R f x e 定义域是 x R 。故选 A.
39.(2009 福建卷文)定义在 R 上的偶函数 f x 的部分图像如右图所示,则在 2,0 上,下列函数中与
f x 的单调性不同的是
( )
A. 2 1y x
B. | | 1y x
C. 3
2 1, 0
1, 0
x x
y
x x
D. ,
, 0
x
x
e x oy
e x
答案 C
解析 解析 根据偶函数在关于原点对称的区间上单调性相反,故可知求在 2,0 上单调递减,注意到要
与 f x 的单调性不同,故所求的函数在 2,0 上应单调递增。而函数 2 1y x 在 ,1 上递减;函数
1y x 在 ,0 时 单 调 递 减 ; 函 数
0,1
0,12
3
xx
xx
y 在 ( ]0, 上 单 调 递 减 , 理 由 如 下
y’=3x2>0(x<0),故函数单调递增, 显然符合题意;而函数
0,
0,
xe
xey x
x
,有 y’=- xe <0(x<0),故其在
( ]0, 上单调递减, 不符合题意,综上选 C。
40.(2009 重庆卷文)把函数 3( ) 3f x x x 的图像 1C 向右平移 u 个单位长度,再向下平移 v 个单位长度
后得到图像 2C .若对任意的 0u ,曲线 1C 与 2C 至多只有一个交点,则 v 的最小值为
( )
A. 2 B. 4 C. 6 D.8
答案 B
解析 根据题意曲线 C 的解析式为 3( ) 3( ) ,y x u x u v 则方程
3 3( ) 3( ) 3x u x u v x x ,即 2 33 ( 3 ) 0ux u u v ,即 31 34v u u 对任意
恒成立,于是 31 34v u u 的最大值,令 31( ) 3 ( 0),4g u u u u 则
23 3(( ) 3 ( 2)( 2)4 4g u u u u 由此知函数 ( )g u 在(0,2)上为增函数,在 (2, ) 上为减函数,
所以当 2u 时,函数 ( )g u 取最大值,即为 4,于是 4v 。
41.(2009 年广东卷文)若函数 ( )y f x 是函数 1xy a a a ( 0,且 )的反函数,且 (2) 1f ,则 ( )f x
( )
A. x2log B. x2
1 C. x
2
1log D.2 2x
答案 A
解析 函数 1xy a a a ( 0,且 )的反函数是 ( ) logaf x x ,又 (2) 1f ,即 log 2 1a ,
所以, 2a ,故 2( ) logf x x ,选 A.
42.(2009 北京文)为了得到函数 3lg 10
xy 的图像,只需把函数 lgy x 的图像上所有
点 ( )
A.向左平移 3 个单位长度,再向上平移 1 个单位长度
B.向右平移 3 个单位长度,再向上平移 1 个单位长度
C.向左平移 3 个单位长度,再向下平移 1 个单位长度
D.向右平移 3 个单位长度,再向下平移 1 个单位长度
答案 C
.w 解析 本题主要考查函数图象的平移变换. 属于基础知识、基本运算的考查.
43.(2009 天津卷文)设 3.0
2
1
3
1 )2
1(,3log,2log cba ,则 ( )
A a 2( )f x
的是
A. ( )f x = 1
x B. ( )f x = 2( 1)x
C . ( )f x = xe D. ( ) ln( 1)f x x
答案 A
解析 依题意可得函数应在 (0, )x 上单调递减,故由选项可得 A 正确。
49. (2009 辽宁卷文)已知函数 ( )f x 满足:x≥4,则 ( )f x = 1( )2
x ;当 x<4 时 ( )f x =
( 1)f x ,则 2(2 log 3)f =
A. 1
24 B. 1
12 C. 1
8 D. 3
8
答案 A
解析 ∵3<2+log23<4,所以 f(2+log23)=f(3+log23)且 3+log23>4
∴ 2(2 log 3)f =f(3+log23)
= 1
2 2 2
1log 33 log 3 log 31 1 1 1 1 1 1 1( ) ( ) ( )2 8 2 8 2 8 3 24
50.(2009 四川卷文)函数 )(2 1 Rxy x 的反函数是
A. )0(log1 2 xxy B. )1)(1(log 2 xxy
C. )0(log1 2 xxy D. )1)(1(log 2 xxy
答案 C
解析 由 yxyxy x
22
1 log1log12 ,又因原函数的值域是 0y ,
∴其反函数是 )0(log1 2 xxy
51.(2009 陕西卷文)设曲线 1 *( )ny x n N 在点(1,1)处的切线与 x 轴的交点的横坐标为 nx ,则
1 2 nx x x 的值为
A. 1
n B. 1
1n C.
1
n
n D.1
答案 B
解析 对 1 * '( ) ( 1)n ny x n N y n x 求导得 ,令 1x 得在点(1,1)处的切线的斜率 1k n ,在点
( 1 , 1 ) 处 的 切 线 方 程 为 1 ( 1) ( 1)( 1)n ny k x n x , 不 妨 设 0y , 1
n
n nx 则
1 2
1 2 3 1 1...2 3 4 1 1n
n nx x x n n n
, 故选 B.
52.(2009 全国卷Ⅰ文)已知函数 ( )f x 的反函数为 ( ) 1 0g x x= +2lgx > ,则 )1()1( gf
(A)0 (B)1 (C)2 (D)4
答案 C
解析 由题令 1lg21 x 得 1x ,即 1)1( f ,又 1)1( g ,所以 2)1()1( gf ,故选择 C。
53.(2009 湖南卷理)若 2log a<0, 1( )2
b >1,则 ( )
A.a>1,b>0 B.a>1,b<0 C. 0<a<1, b>0 D. 0<a<1, b<0
答案 D
解析 由 2log 0a 得 0 ,a 由 1( ) 12
b 得 0b ,所以选 D 项。
54.(2009 四川卷理)已知函数
2
2
log ( 2 )
( ) 24 ( 22
a x x
f x xx xx
当 时
在点 处
当 时)
连续,则常数 a
的值是 ( )
A.2 B.3 C.4 D.5
【考点定位】本小题考查函数的连续性,考查分段函数,基础题。
答案 B
解析 由题得 3222log 2 aa ,故选择 B。
解析 2:本题考查分段函数的连续性.由
2
2 2 2
4lim ( ) lim lim( 2) 42x x x
xf x xx
, 2
2(2) log 1f a a ,
由函数的连续性在一点处的连续性的定义知
2
(2) lim ( ) 4x
f f x
,可得 3a .故选 B.
55.(2009 福建卷文)若函数 f x 的零点与 4 2 2xg x x 的零点之差的绝对值不超过 0.25,则 f x
可以是
A. 4 1f x x B. 2( 1)f x x
C. 1xf x e D. 1
2f x In x
答案 A
解 析 4 1f x x 的 零 点 为 x=
4
1 , 2( 1)f x x 的 零 点 为 x=1, 1xf x e 的 零 点 为 x=0,
1
2f x In x
的零点为 x=
2
3 .现在我们来估算 4 2 2xg x x 的零点,因 为 g(0)= -1,g(
2
1 )=1,所
以 g(x)的零点 x(0,
2
1 ),又函数 f x 的零点与 4 2 2xg x x 的零点之差的绝对值不超过 0.25,只有
4 1f x x 的零点适合,故选 A。
56.(2009 年广东卷文)函数 xexxf )3()( 的单调递增区间是 ( )
A. )2,( B.(0,3) C.(1,4) D. ),2(
答案 D
解析 ( ) ( 3) ( 3) ( 2)x x xf x x e x e x e ,令 ( ) 0f x ,解得 2x ,故选 D
57.(2009 全国卷Ⅰ理) 已知直线 y=x+1 与曲线 y ln( )x a 相切,则α的值为( )
A.1 B. 2 C.-1 D.-2
答案 B
解:设切点 0 0( , )P x y ,则 0 0 0 0ln1, ( )y x ay x ,又
0
'
0
1| 1x xy x a
0 0 01 0, 1 2x a y x a .故答案 选 B
58.(2009 安徽卷理)已知函数 ( )f x 在 R 上满足 2( ) 2 (2 ) 8 8f x f x x x ,则曲线
( )y f x 在点 (1, (1))f 处的切线方程是 ( )
A. 2 1y x B. y x C. 3 2y x D. 2 3y x
答案 A
解析 由 2( ) 2 (2 ) 8 8f x f x x x 得几何 2(2 ) 2 ( ) (2 ) 8(2 ) 8f x f x x x ,
即 22 ( ) (2 ) 4 4f x f x x x , ∴ 2( )f x x ∴ / ( ) 2f x x , ∴ 切 线 方 程 1 2( 1)y x , 即
2 1 0x y 选 A
59.(2009 江西卷文)若存在过点 (1,0) 的直线与曲线 3y x 和 2 15 94y ax x 都相切,则 a 等于
( )
A. 1 或 25- 64 B. 1 或 21
4 C. 7
4
或 25- 64 D. 7
4
或 7
答案 A
解析 设过 (1,0) 的直线与 3y x 相切于点 3
0 0( , )x x ,所以切线方程为
3 2
0 0 03 ( )y x x x x
即 2 3
0 03 2y x x x ,又 (1,0) 在切线上,则 0 0x 或 0
3
2x ,
当 0 0x 时,由 0y 与 2 15 94y ax x 相切可得 25
64a ,
当 0
3
2x 时,由 27 27
4 4y x 与 2 15 94y ax x 相切可得 1a ,所以选 A .
60.(2009 江西卷理)设函数 2( ) ( )f x g x x ,曲线 ( )y g x 在点 (1, (1))g 处的切线方程为 2 1y x ,
则曲线 ( )y f x 在点 (1, (1))f 处切线的斜率为 ( )
A. 4 B. 1
4
C. 2 D. 1
2
答案 A
解析 由已知 (1) 2g ,而 ( ) ( ) 2f x g x x ,所以 (1) (1) 2 1 4f g 故选 A
力。
61.(2009 全国卷Ⅱ理)曲线
2 1
xy x
在点 1,1 处的切线方程为 ( )
A. 2 0x y B. 2 0x y
C. 4 5 0x y D. 4 5 0x y
答案 B
解 1 1 12 2
2 1 2 1| | [ ]| 1(2 1) (2 1)x x x
x xy x x
,
故切线方程为 1 ( 1)y x ,即 2 0x y 故选 B.
62.(2009 湖南卷文)若函数 ( )y f x 的导函数在区间[ , ]a b 上是增函数,
则函数 ( )y f x 在区间[ , ]a b 上的图象可能是 ( )
A . B. C. D.
解析 因为函数 ( )y f x 的导函数 ( )y f x 在区间[ , ]a b 上是增函数,即在区间[ , ]a b 上各点处的斜率 k
是递增的,由图易知选 A. 注意 C 中 y k 为常数噢.
63.(2009 辽宁卷理)若 1x 满足 2x+ 2x =5, 2x 满足 2x+2 2log (x-1)=5, 1x + 2x = ( )
A. 5
2 B.3 C. 7
2 D.4
答案 C
解析 由题意 1
12 2 5xx ①
2 2 22 2log ( 1) 5x x ②
所以 1
12 5 2x x , 1 2 1log (5 2 )x x
即 2 1 2 12log (5 2 )x x
令 2x1=7-2t,代入上式得 7-2t=2log2(2t-2)=2+2log2(t-1)
∴5-2t=2log2(t-1)与②式比较得 t=x2
于是 2x1=7-2x2
64.(2009 天津卷理)设函数 1( ) ln ( 0),3f x x x x 则 ( )y f x ( )
A 在区间 1( ,1),(1, )ee
内均有零点。
B 在区间 1( ,1),(1, )ee
内均无零点。
C 在区间 1( ,1)e
内有零点,在区间 (1, )e 内无零点。
D 在区间 1( ,1)e
内无零点,在区间 (1, )e 内有零点。
【考点定位】本小考查导数的应用,基础题。
解析 由题得
x
x
xxf 3
31
3
1)`( ,令 0)`( xf 得 3x ;令 0)`( xf 得
ababa o xo x
y
ba o x
y
o x
y
b
y
30 x ; 0)`( xf 得 3x ,故知函数 )(xf 在区间 )3,0( 上为减函数,在区间 ),3(
为增函数,在点 3x 处有极小值 03ln1 ;又
013
1)1(,013,3
1)1(
eefeeff ,故选择 D。
二、填空题
65.(2009 江苏卷)已知集合 2log 2 , ( , )A x x B a ,若 A B 则实数 a 的取值范围是 ( , )c ,
其中 c = .
解析 考查集合的子集的概念及利用对数的性质解不等式。
由 2log 2x 得 0 4x , (0,4]A ;由 A B 知 4a ,所以 c 4。
66.(2009 山东卷理)若函数 f(x)=a x -x-a(a>0 且 a 1)有两个零点,则实数 a 的取值范围是 .
答案 }1|{ aa
解析 设函数 ( 0,xy a a 且 1}a 和函数 y x a ,则函数 f(x)=a x -x-a(a>0 且 a 1)有两个零点, 就是
函数 ( 0,xy a a 且 1}a 与函数 y x a 有两个交点,由图象可知当 10 a 时两函数只有一个交点,
不符合,当 1a 时,因为函数 ( 1)xy a a 的图象过点(0,1),而直线 y x a 所过的点一定在点(0,1)的上方,
所以一定有两个交点.所以实数 a 的取值范围是 1a
【命题立意】:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数
的不同取值范围而分别画出函数的图象进行解答.
67. ( 2009 重 庆 卷 文 ) 记 3( ) log ( 1)f x x 的 反 函 数 为 1( )y f x , 则 方 程 1( ) 8f x 的 解
x .
答案 2
解法 1 由 3( ) log ( 1)y f x x ,得 13yx ,即 1( ) 3 1f x x ,于是由3 1 8x ,解得 2x
解法 2 因为 1( ) 8f x ,所以 3(8) log (8 1) 2x f
68.(2009 重庆卷理)若 1( ) 2 1xf x a
是奇函数,则 a .
答案 1
2
解析 解法 1 1 2( ) , ( ) ( )2 1 1 2
x
x xf x a a f x f x
2 1 1 2 1( ) 2 11 2 2 1 1 2 1 2 2
x x
x x x xa a a a
故
69.(2009 上海卷文) 函数 f(x)=x3+1 的反函数 f-1(x)=_____________.
答案 3 1x
解析 由 y=x3+1,得 x= 3 1y ,将 y 改成 x,x 改成 y 可得答案。
70. ( 2009 北 京 文 ) 已 知 函 数 3 , 1,( )
, 1,
x xf x
x x
若 ( ) 2f x , 则 x .
答案 3log 2
解析 5.u.c 本题主要考查分段函数和简单的已知函数值求 x 的值. 属于基础知识、基本运算的考查.
由 3
1
log 2
3 2x
x
x
, 1
2 2
x
x x
无解,故应填 3log 2 .
71.(2009 北京理)若函数
1 , 0
( ) 1( ) , 03
x
xxf x
x
则不等式 1| ( ) | 3f x 的解集为____________.
答案 3,1
解析 本题主要考查分段函数和简单绝对值不等式的解法. 属于基础知识、基本运算
的考查.
(1)由
0
1| ( ) | 3 01 13 3
x
f x x
x
.
(2)由
0 0
1| ( ) | 0 11 1 1 13 3 3 3 3
x x
x x
f x x
.
∴不等式 1| ( ) | 3f x 的解集为 | 3 1x x ,∴应填 3,1 .
72.(2009 江苏卷)已知 5 1
2a ,函数 ( ) xf x a ,若实数 m 、 n 满足 ( ) ( )f m f n ,则 m 、 n 的大
小关系为 .
解析 考查指数函数的单调性。
5 1 (0,1)2a ,函数 ( ) xf x a 在 R 上递减。由 ( ) ( )f m f n 得:m0)在区间 8,8 上有四个不同的根 1 2 3 4, , ,x x x x ,则 1 2 3 4 _________.x x x x
答案 -8
解析 因为定义在 R 上的奇函数,满足 ( 4) ( )f x f x ,所以 ( 4) ( )f x f x ,所以, 由 )(xf 为奇函数,
所以函数图象关于直线 2x 对称且 (0) 0f ,由 ( 4) ( )f x f x 知 ( 8) ( )f x f x ,所以函数是以 8 为
周期的周期函数,又因为 )(xf 在区间[0,2]上是增函数,所以 )(xf 在区间[-2,0]上也是增函数.如图所示,那么
方程 f(x)=m(m>0)在区间 8,8 上有四个不同的根 1 2 3 4, , ,x x x x ,不妨设 1 2 3 4x x x x 由对称性知
1 2 12x x 3 4 4x x 所以 1 2 3 4 12 4 8x x x x
【命题立意】:本题综合考查了函数的奇偶性,单调性,
对称性,周期性,以及由函数图象解答方程问题,
运用数形结合的思想和函数与方程的思想解答问题.
74.(2009四川卷文)设V 是已知平面 M 上所有向量的集合,对于映射 : ,f V V a V ,记 a 的象为 ( )f a 。
若映射 :f V V 满足:对所有 a b V、 及任意实数 , 都有 ( ) ( ) ( )f a b f a f b ,则 f 称为
平面 M 上的线性变换。现有下列命题:
①设 f 是平面 M 上的线性变换, a b V、 ,则 ( ) ( ) ( )f a b f a f b
②若 e 是平面 M 上的单位向量,对 , ( )a V f a a e 设 ,则 f 是平面 M 上的线性变换;
③对 , ( )a V f a a 设 ,则 f 是平面 M 上的线性变换;
④设 f 是平面 M 上的线性变换, a V ,则对任意实数 k 均有 ( ) ( )f ka kf a 。
其中的真命题是 (写出所有真命题的编号)
答案 ①③④
解析 ①:令 1 ,则 )()()( bfafbaf 故①是真命题
同理,④:令 0, k ,则 )()( akfkaf 故④是真命题
③:∵ aaf )( ,则有 bbf )(
)()()()()()( bfafbababaf 是线性变换,故③是真命题
-8 -6 -4 -2 0 2 4 6 8
y
x
f(x)=m (m>0)
②:由 eaaf )( ,则有 ebbf )(
ebfafeebeaebabaf )()()()()()(
∵ e 是单位向量, e ≠0,故②是假命题
【备考提示】本小题主要考查函数,对应及高等数学线性变换的相关知识,试题立意新
颖,突出创新能力和数学阅读能力,具有选拔性质。
75.(2009 福建卷文)若函数 f x 的零点与 4 2 2xg x x 的零点之差的绝对值不超过 0.25,则 f x
可以是
A. 4 1f x x B. 2( 1)f x x
C. 1xf x e D. 1
2f x In x
答案 A
解 析 4 1f x x 的 零 点 为 x=
4
1 , 2( 1)f x x 的 零 点 为 x=1, 1xf x e 的 零 点 为 x=0,
1
2f x In x
的零点为 x=
2
3 .现在我们来估算 4 2 2xg x x 的零点,因为 g(0)= -1,g(
2
1 )=1,所以
g(x)的零点 x(0,
2
1 ),又函数 f x 的零点与 4 2 2xg x x 的零点之差的绝对值不超过 0.25,只有
4 1f x x 的零点适合,故选 A。
76.(2009 山东卷文)若函数 f(x)=a x -x-a(a>0 且 a 1)有两个零点,则实数 a 的取值范围是 .
答案 }1|{ aa
解析 设函数 ( 0,xy a a 且 1}a 和函数 y x a ,则函数 f(x)=a x -x-a(a>0 且 a 1)有两个零点, 就是
函数 ( 0,xy a a 且 1}a 与函数 y x a 有两个交点,由图象可知当 10 a 时两函数只有一个交点,
不符合,当 1a 时,因为函数 ( 1)xy a a 的图象过点(0,1),而直线 y x a 所过的点(0,a)一定在点(0,1)
的上方,所以一定有两个交点.所以实数 a 的取值范围是 }1|{ aa .
【命题立意】:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数
的不同取值范围而分别画出函数的图象进行解答
77.(2009 辽宁卷文)若函数
2
( ) 1
x af x x
在 1x 处取极值,则 a
解析 f’(x)=
2
2
2 ( 1) ( )
( 1)
x x x a
x
f’(1)= 3
4
a =0 a=3
答案 3
78.若曲线 2f x ax Inx 存在垂直于 y 轴的切线,则实数 a 的取值范围是 .
解析 解析 由题意该函数的定义域 0x ,由 12f x ax x
。因为存在垂直于 y 轴的切线,故此
时斜率为 0 ,问题转化为 0x 范围内导函数 12f x ax x
存在零点。
解法 1 (图像法)再将之转化为 2g x ax 与 1h x x
存在交点。当 0a 不符合题意,当 0a 时,
如图 1,数形结合可得显然没有交点,当 0a 如图 2,此时正好有一个交点,故有 0a 应填 ,0
或是 | 0a a 。
解法 2 (分离变量法)上述也可等价于方程 12 0ax x
在 0, 内有解,显然可得 2
1 ,02a x
79.(2009 江苏卷)函数 3 2( ) 15 33 6f x x x x 的单调减区间为 .
解析 考查利用导数判断函数的单调性。
2( ) 3 30 33 3( 11)( 1)f x x x x x ,
由 ( 11)( 1) 0x x 得单调减区间为 ( 1,11) 。亦可填写闭区间或半开半闭区间。
80.(2009 江苏卷)在平面直角坐标系 xoy 中,点 P 在曲线 3: 10 3C y x x 上,且在第二象限内,已知
曲线 C 在点 P 处的切线的斜率为 2,则点 P 的坐标为 .
解析 考查导数的几何意义和计算能力。
23 10 2 2y x x ,又点 P 在第二象限内, 2x 点 P 的坐标为(-2,15)
答案 : 1a
【命题立意】:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数
的不同取值范围而分别画出函数的图象解答.
81.(2009 福建卷理)若曲线 3( ) lnf x ax x 存在垂直于 y 轴的切线,则实数 a 取值范围是_____________.
答案 ( ,0)
解析 由题意可知 ' 2 1( ) 2f x ax x
,又因为存在垂直于 y 轴的切线,
所以 2
3
1 12 0 ( 0) ( ,0)2ax a x ax x
。
82.(2009 陕西卷理)设曲线 1 *( )ny x n N 在点(1,1)处的切线与 x 轴的交点的横坐标为 nx ,令 lgn na x ,
则 1 2 99a a a 的值为 .
答案 -2
1 *
1
1
1 2 99 1 2 99
( )
' ( 1) '| 1 1 ( 1)( 1)
1
1 2 98 99 1... lg ... lg ... lg 22 3 99 100 100
n
n n
x
n
y x n N
y x y n x y n y n x
nx n
a a a x x x
解析:点(1,1)在函数 的图像上,(1,1)为切点,
的导函数为 切线是:
令y=0得切点的横坐标:
83.(2009四川卷文)设V 是已知平面 M 上所有向量的集合,对于映射 : ,f V V a V ,记 a 的象为 ( )f a 。
若映射 :f V V 满足:对所有 a b V、 及任意实数 , 都有 ( ) ( ) ( )f a b f a f b ,则 f 称为
平面 M 上的线性变换。现有下列命题:
①设 f 是平面 M 上的线性变换, a b V、 ,则 ( ) ( ) ( )f a b f a f b
②若 e 是平面 M 上的单位向量,对 , ( )a V f a a e 设 ,则 f 是平面 M 上的线性变换;
③对 , ( )a V f a a 设 ,则 f 是平面 M 上的线性变换;
④设 f 是平面 M 上的线性变换, a V ,则对任意实数 k 均有 ( ) ( )f ka kf a 。
其中的真命题是 (写出所有真命题的编号)
答案 ①③④
解析 ①:令 1 ,则 )()()( bfafbaf 故①是真命题
同理,④:令 0, k ,则 )()( akfkaf 故④是真命题
③:∵ aaf )( ,则有 bbf )(
)()()()()()( bfafbababaf 是线性变换,故③是真命题
②:由 eaaf )( ,则有 ebbf )(
ebfafeebeaebabaf )()()()()()(
∵ e 是单位向量, e ≠0,故②是假命题
【备考提示】本小题主要考查函数,对应及高等数学线性变换的相关知识,试题立意新颖,
突出创新能力和数学阅读能力,具有选拔性质。
84.(2009 宁夏海南卷文)曲线 2 1xy xe x 在点(0,1)处的切线方程为 。
答案 3 1y x
解析 2' xx xeey ,斜率 k= 200 e =3,所以,y-1=3x,即 3 1y x
三、解答题
85.(2009 年广东卷文)(本小题满分 14 分)
已知二次函数 )(xgy 的导函数的图像与直线 2y x 平行,且 )(xgy 在 x =-1 处取得最小值 m-
1(m 0 ).设函数
x
xgxf )()(
(1)若曲线 )(xfy 上的点 P 到点 Q(0,2)的距离的最小值为 2 ,求 m 的值
(2) )( Rkk 如何取值时,函数 kxxfy )( 存在零点,并求出零点.
解 (1)设 2g x ax bx c ,则 2g x ax b ;
又 g x 的图像与直线 2y x 平行 2 2a 1a
又 g x 在 1x 取极小值, 12
b , 2b
1 1 2 1g a b c c m , c m ;
2g x mf x xx x
, 设 ,o oP x y
则
2
2 22 2
0 0 0 0
0
2 mPQ x y x x x
2
2 2
0 2
0
2 2 2 2 2mx mx
22 2 2 4m 2
2m ;
(2)由 1 2 0my f x kx k x x
,
得 21 2 0k x x m *
当 1k 时,方程 * 有一解
2
mx ,函数 y f x kx 有一零点
2
mx ;
当 1k 时,方程 * 有二解 4 4 1 0m k ,若 0m , 11k m
,
函数 y f x kx 有两个零点
2 4 4 1 1 1 1
2 1 1
m k m kx k k
;若 0m ,
11k m
,函数 y f x kx 有两个零点
2 4 4 1 1 1 1
2 1 1
m k m kx k k
;
当 1k 时,方程 * 有一解 4 4 1 0m k , 11k m
, 函数 y f x kx 有一零点
1
1x k
86.(2009 浙江理)(本题满分 14 分)已知函数 3 2 2( ) ( 1) 5 2f x x k k x x , 2 2( ) 1g x k x kx ,
其中 k R .
(I)设函数 ( ) ( ) ( )p x f x g x .若 ( )p x 在区间 (0,3) 上不单调,求 k 的取值范围;
(II)设函数 ( ), 0,( ) ( ), 0.
g x xq x f x x
是否存在 k ,对任意给定的非零实数 1x ,存在惟一
的非零实数 2x ( 2 1x x ),使得 2 1( ) ( )q x q x 成立?若存在,求 k 的值;若不存
在,请说明理由.
解 (I)因 3 2( ) ( ) ( ) ( 1) ( 5) 1P x f x g x x k x k , 23 2( 1) ( 5)p x x k x k ,因 ( )p x
在 区 间 (0,3) 上 不 单 调 , 所 以 0p x 在 0,3 上 有 实 数 解 , 且 无 重 根 , 由 0p x 得
2(2 1) (3 2 5),k x x x
2(3 2 5) 3 9 102 12 1 4 2 1 3
x xk xx x
,令 2 1,t x 有 1,7t ,记 9( ) ,h t t t
则 h t
在 1,3 上单调递减,在 3,7 上单调递增,所以有 6,10h t , 于是 92 1 6,102 1x x
,得
5, 2k , 而 当 2k 时 有 0p x 在 0,3 上 有 两 个 相 等 的 实 根 1x , 故 舍 去 , 所 以
5, 2k ;
(II)当 0x 时有 2 23 2( 1) 5q x f x x k k x ;
当 0x 时有 22q x g x k x k ,因为当 0k 时不合题意,因此 0k ,
下面讨论 0k 的情形,记 A ( , )k ,B= 5, (ⅰ)当 1 0x 时, q x 在 0, 上单调递增,所
以要使 2 1q x q x 成立,只能 2 0x 且 A B ,因此有 5k ,(ⅱ)当 1 0x 时, q x 在 0,
上单调递减,所以要使 2 1q x q x 成立,只能 2 0x 且 A B ,因此 5k ,综合(ⅰ)(ⅱ) 5k ;
当 5k 时 A=B,则 1 10,x q x B A ,即 2 0,x 使得 2 1q x q x 成立,因为 q x 在 0,
上单调递增,所以 2x 的值是唯一的;
同理, 1 0x ,即存在唯一的非零实数 2 2 1( )x x x ,要使 2 1q x q x 成立,所以 5k 满足题意.
87.(2009 江苏卷)(本小题满分 16 分)
设 a 为实数,函数 2( ) 2 ( ) | |f x x x a x a .
(1)若 (0) 1f ,求 a 的取值范围;
(2)求 ( )f x 的最小值;
(3)设函数 ( ) ( ), ( , )h x f x x a ,直接写出(不需给出演算步骤)不等式 ( ) 1h x 的解集.
解 本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、
分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分 16 分
(1)若 (0) 1f ,则 2
0
| | 1 1
1
a
a a a
a
(2)当 x a 时, 2 2( ) 3 2 ,f x x ax a
2
2min
( ), 0 2 , 0
( ) 2( ), 0 , 03 3
f a a a a
f x a af a a
当 x a 时, 2 2( ) 2 ,f x x ax a
2
min 2
( ), 0 2 , 0( ) ( ), 0 2 , 0
f a a a af x f a a a a
综上
2
2min
2 , 0
( ) 2 , 03
a a
f x a a
(3) ( , )x a 时, ( ) 1h x 得 2 23 2 1 0x ax a ,
2 2 24 12( 1) 12 8a a a
当 6 6
2 2a a 或 时, 0, ( , )x a ;
当 6 6
2 2a 时,△>0,得:
2 23 2 3 2( )( ) 03 3
a a a ax x
x a
讨论得:当 2 6( , )2 2a 时,解集为 ( , )a ;
当 6 2( , )2 2a 时,解集为
2 23 2 3 2( , ] [ , )3 3
a a a aa ;
当 2 2[ , ]2 2a 时,解集为
23 2[ , )3
a a .
88.(2009 年上海卷理)已知函数 ( )y f x 的反函数。定义:若对给定的实数 ( 0)a a ,函数 ( )y f x a
与 1( )y f x a 互为反函数,则称 ( )y f x 满足“ a 和性质”;若函数 ( )y f ax 与 1( )y f ax 互为反
函数,则称 ( )y f x 满足“ a 积性质”。
判断函数 2( ) 1( 0)g x x x 是否满足“1 和性质”,并说明理由;
求所有满足“2 和性质”的一次函数;
设函数 ( )( 0)y f x x 对任何 0a ,满足“ a 积性质”。求 ( )y f x 的表达式。
解 (1)函数 2( ) 1( 0)g x x x 的反函数是 1( ) 1( 1)g x x x
1( 1) ( 0)g x x x
而 2( 1) ( 1) 1( 1),g x x x 其反函数为 1 1( 1)y x x
故函数 2( ) 1( 0)g x x x 不满足“1 和性质”
(2)设函数 ( ) ( )f x kx b x R 满足“2 和性质”, 0.k
1 1 2( ) ( ), ( 2)x b x bf x x R f xk k
…….6 分
而 ( 2) ( 2) ( ),f x k x b x R 得反函数 2x b ky k
………….8 分
由“2 和性质”定义可知 2x b
k
= 2x b k
k
对 x R 恒成立
1, ,k b R 即所求一次函数为 ( ) ( )f x x b b R ………..10 分
(3)设 0a , 0 0x ,且点 0 0( , )x y 在 ( )y f ax 图像上,则 0 0( , )y x 在函数 1( )y f ax 图象上,
故 0 0( )f ax y ,可得 0 0 0( ) ( )ay f x af ax , ......12 分
1
0 0( )f ay x
令 0ax x ,则
0
xa x
。 0
0
( ) ( )xf x f xx
,即 0 0( )( ) x f xf x x
。 ......14 分
综上所述, 1
11 n
nb q b ( ) ( 0)kf x kx
,此时 ( ) kf ax ax
,其反函数就是 ky ax
,
而 1( ) kf ax ax
,故 ( )y f ax 与 1( )y f ax 互为反函数 。
89.(2009 全国卷Ⅰ理)本小题满分 12 分。(注意:在试题卷上作答无效)
设函数 3 23 3f x x bx cx 在两个极值点 1 2x x、 ,且 1 2[ 1 0], [1,2].x x ,
(I)求 b c、 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 ,b c 的区域;
(II)证明: 2
110 2f x
分析(I)这一问主要考查了二次函数根的分布及线性规划作可行域的能力。
大 部 分 考 生 有 思 路 并 能 够 得 分 。
23 6 3f x x bx c 由 题 意 知 方 程
0f x 有两个根 1 2x x、
1 [ 1 0],x 且 , 2 [1,2].x 则有 1 0f ,
0 0f , 1 0 2 0f f , 故有
右图中阴影部分即
是满足这些条件的
点 ,b c 的区域。
(II)这一问考生不易
得分,有一定的区分度。主要原因是含字母
较多,不易找到突破口。此题主要利用消元
的 手 段 , 消 去 目 标
3 2
2 2 2 23 3f x x bx cx 中的b ,(如果消 c 会较繁琐)再利用 2x 的范围,并借助(I)中的约束条件得
[ 2,0]c 进而求解,有较强的技巧性。
解析 由题意有 2
2 2 23 6 3 0f x x bx c ............①
又 3 2
2 2 2 23 3f x x bx cx .....................②
�
c
�
b
消去 b 可得 3
2 2 2
1 3
2 2
cf x x x .
又 2 [1,2]x ,且 [ 2,0]c 2
110 ( ) 2f x
90.(2009 浙江文)(本题满分 15 分)已知函数 3 2( ) (1 ) ( 2)f x x a x a a x b ( , )a b R .
(I)若函数 ( )f x 的图象过原点,且在原点处的切线斜率是 3 ,求 ,a b 的值;
(II)若函数 ( )f x 在区间 ( 1,1) 上不单调,求 a 的取值范围.
解析 (Ⅰ)由题意得 )2()1(23)( 2 aaxaxxf
又
3)2()0(
0)0(
aaf
bf ,解得 0b , 3a 或 1a
(Ⅱ)函数 )(xf 在区间 )1,1( 不单调,等价于
导函数 )(xf 在 )1,1( 既能取到大于 0 的实数,又能取到小于 0 的实数
即函数 )(xf 在 )1,1( 上存在零点,根据零点存在定理,有
0)1()1( ff , 即: 0)]2()1(23)][2()1(23[ aaaaaa
整理得: 0)1)(1)(5( 2 aaa ,解得 15 a
91.(2009 北京文)(本小题共 14 分)
设函数 3( ) 3 ( 0)f x x ax b a .
(Ⅰ)若曲线 ( )y f x 在点 (2, ( ))f x 处与直线 8y 相切,求 ,a b 的值;
(Ⅱ)求函数 ( )f x 的单调区间与极值点.
解析 本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问
题的能力.
(Ⅰ) ' 23 3f x x a ,
∵曲线 ( )y f x 在点 (2, ( ))f x 处与直线 8y 相切,
∴
' 2 0 3 4 0 4,
24.8 6 82 8
f a a
ba bf
(Ⅱ)∵ ' 23 0f x x a a ,
当 0a 时, ' 0f x ,函数 ( )f x 在 , 上单调递增,
此时函数 ( )f x 没有极值点.
当 0a 时,由 ' 0f x x a ,
当 ,x a 时, ' 0f x ,函数 ( )f x 单调递增,
当 ,x a a 时, ' 0f x ,函数 ( )f x 单调递减,
当 ,x a 时, ' 0f x ,函数 ( )f x 单调递增,
∴此时 x a 是 ( )f x 的极大值点, x a 是 ( )f x 的极小值点.
92.(2009 北京理)(本小题共 13 分)
设函数 ( ) ( 0)kxf x xe k
(Ⅰ)求曲线 ( )y f x 在点 (0, (0))f 处的切线方程;
(Ⅱ)求函数 ( )f x 的单调区间;
(Ⅲ)若函数 ( )f x 在区间 ( 1,1) 内单调递增,求 k 的取值范围.
解析 本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查
综合分析和解决问题的能力.
(Ⅰ) ' '1 , 0 1, 0 0kxf x kx e f f ,
曲线 ( )y f x 在点 (0, (0))f 处的切线方程为 y x .
(Ⅱ)由 ' 1 0kxf x kx e ,得 1 0x kk
,
若 0k ,则当 1,x k
时, ' 0f x ,函数 f x 单调递减,
当 1 , ,x k
时, ' 0f x ,函数 f x 单调递增,
若 0k ,则当 1,x k
时, ' 0f x ,函数 f x 单调递增,
当 1 , ,x k
时, ' 0f x ,函数 f x 单调递减,
(Ⅲ)由(Ⅱ)知,若 0k ,则当且仅当 1 1k
,
即 1k 时,函数 f x 1,1 内单调递增,
若 0k ,则当且仅当 1 1k
,
即 1k 时,函数 f x 1,1 内单调递增,
综上可知,函数 f x 1,1 内单调递增时, k 的取值范围是 1,0 0,1 .
93.(2009 山东卷文)(本小题满分 12 分)
已知函数 3 21( ) 33f x ax bx x ,其中 0a
(1)当 ba, 满足什么条件时, )(xf 取得极值?
(2)已知 0a ,且 )(xf 在区间 (0,1]上单调递增,试用 a 表示出b 的取值范围.
解: (1)由已知得 2'( ) 2 1f x ax bx ,令 0)(' xf ,得 2 2 1 0ax bx ,
)(xf 要取得极值,方程 2 2 1 0ax bx 必须有解,
所以△ 24 4 0b a ,即 2b a , 此时方程 2 2 1 0ax bx 的根为
2 2
1
2 4 4
2
b b a b b ax a a
,
2 2
2
2 4 4
2
b b a b b ax a a
,
所以 1 2'( ) ( )( )f x a x x x x
当 0a 时,
x (-∞,x1) x 1 (x1,x2) x2 (x2,+∞)
f’(x) + 0 - 0 +
f (x) 增函数 极大值 减函数 极小值 增函数
所以 )(xf 在 x 1, x2 处分别取得极大值和极小值.
当 0a 时,
x (-∞,x2) x 2 (x2,x1) x1 (x1,+∞)
f’(x) - 0 + 0 -
f (x) 减函数 极小值 增函数 极大值 减函数
所以 )(xf 在 x 1, x2 处分别取得极大值和极小值.
综上,当 ba, 满足 2b a 时, )(xf 取得极值.
(2)要使 )(xf 在区间 (0,1]上单调递增,需使 2'( ) 2 1 0f x ax bx 在 (0,1]上恒成立.
即 1 , (0,1]2 2
axb xx
恒成立, 所以 max
1( )2 2
axb x
设 1( ) 2 2
axg x x
,
2
2 2
1( )1'( ) 2 2 2
a xa ag x x x
,
令 '( ) 0g x 得 1x
a
或 1x
a
(舍去),
当 1a 时, 10 1a
,当 1(0, )x
a
时 '( ) 0g x , 1( ) 2 2
axg x x
单调增函数;
当 1( ,1]x
a
时 '( ) 0g x , 1( ) 2 2
axg x x
单调减函数,
所以当 1x
a
时, ( )g x 取得最大,最大值为 1( )g a
a
.
所以 b a
当 0 1a 时,
1 1
a
,此时 '( ) 0g x 在区间 (0,1]恒成立,所以 1( ) 2 2
axg x x
在区间 (0,1]上单调递增,
当 1x 时 ( )g x 最大,最大值为 1(1) 2
ag ,所以 1
2
ab
综上,当 1a 时, b a ; 当 0 1a 时, 1
2
ab
【命题立意】:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单
调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的
思想,化归思想和分类讨论的思想解答问题.
94.设函数 3 21( ) (1 ) 4 243f x x a x ax a ,其中常数 a>1
(Ⅰ)讨论 f(x)的单调性;
(Ⅱ)若当 x≥0 时,f(x)>0 恒成立,求 a 的取值范围。
解析 本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析
导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求
出的范围。
解析 (I) )2)(2(4)1(2)( 2 axxaxaxxf
由 1a 知,当 2x 时, 0)( xf ,故 )(xf 在区间 )2,( 是增函数;
当 ax 22 时, 0)( xf ,故 )(xf 在区间 )2,2( a 是减函数;
当 ax 2 时, 0)( xf ,故 )(xf 在区间 ),2( a 是增函数。
综上,当 1a 时, )(xf 在区间 )2,( 和 ),2( a 是增函数,在区间 )2,2( a 是减函数。
(II)由(I)知,当 0x 时, )(xf 在 ax 2 或 0x 处取得最小值。
aaaaaaaf 2424)2)(1()2(3
1)2( 23
aaa 2443
4 23
af 24)0(
由假设知
,0)0(
,0)2(
1
f
af
a
即
.024
,0)6)(3(3
4
,1
a
aaa
a
解得 11 时, 1 2 1a
当 x 变化时, '( )f x 与 ( )f x 的变化情况如下表:
x ( ,1 2 )a (1 2 , 1)a ( 1, )
'( )f x + - +
( )f x 单调递增 单调递减 单调递增
由此得,函数 ( )f x 的单调增区间为 ( ,1 2 )a 和 ( 1, ) ,单调减区间为 (1 2 , 1)a 。
②当 1a 时,1 2 1a 此时有 '( ) 0f x 恒成立,且仅在 1x 处 '( ) 0f x ,故函数 ( )f x 的单调增
区间为 R
③当 1a 时,1 2 1a 同理可得,函数 ( )f x 的单调增区间为 ( , 1) 和 (1 2 , )a ,单调减区间为
( 1,1 2 )a
综上:
当 1a 时,函数 ( )f x 的单调增区间为 ( ,1 2 )a 和 ( 1, ) ,单调减区间为 (1 2 , 1)a ;
当 1a 时,函数 ( )f x 的单调增区间为 R;
当 1a 时,函数 ( )f x 的单调增区间为 ( , 1) 和 (1 2 , )a ,单调减区间为 ( 1,1 2 )a .
(Ⅱ)由 1a 得 3 21( ) 33f x x x x 令 2( ) 2 3 0f x x x 得 1 21, 3x x
由(1)得 ( )f x 增区间为 ( , 1) 和 (3, ) ,单调减区间为 ( 1,3) ,所以函数 ( )f x 在处 1 21, 3x x
取得极值,故 M( 51, 3
)N(3, 9 )。
观察 ( )f x 的图象,有如下现象:
①当 m 从-1(不含-1)变化到 3 时,线段 MP 的斜率与曲线 ( )f x 在点 P 处切线的斜率 ( )f x 之差 Kmp- '( )f m
的值由正连续变为负。
②线段 MP 与曲线是否有异于 H,P 的公共点与 Kmp- '( )f m 的 m 正负有着密切的关联;
③Kmp- '( )f m =0 对应的位置可能是临界点,故推测:满足 Kmp- '( )f m 的 m 就是所求的 t 最小值,下
面给出证明并确定的 t 最小值.曲线 ( )f x 在点 ( , ( ))P m f m 处的切线斜率 2'( ) 2 3f m m m ;
线段 MP 的斜率 Kmp
2 4 5
3
m m
当 Kmp- '( )f m =0 时,解得 1 2m m 或
直线 MP 的方程为
2 24 5 4( )3 3
m m m my x
令
2 24 5 4( ) ( ) ( )3 3
m m m mg x f x x
当 2m 时, 2'( ) 2g x x x 在 ( 1,2) 上只有一个零点 0x ,可判断 ( )f x 函数在 ( 1,0) 上单调递增,
在 (0,2) 上单调递减,又 ( 1) (2) 0g g ,所以 ( )g x 在 ( 1,2) 上没有零点,即线段 MP 与曲线 ( )f x 没
有异于 M,P 的公共点。
当 2,3m 时,
2 4(0) 03
m mg . 2(2) ( 2) 0g m
所以存在 0,2m 使得 ( ) 0g
即当 2,3 ,m 时 MP 与曲线 ( )f x 有异于 M,P 的公共点
综上,t 的最小值为 2.
(2)类似(1)于中的观察,可得 m 的取值范围为 1,3
解法二:
(1)同解法一.
(2)由 1a 得 3 21( ) 33f x x x x ,令 2'( ) 2 3 0f x x x ,得 1 21, 3x x
由(1)得的 ( )f x 单调增区间为 ( , 1) 和 (3, ) ,单调减区间为 ( 1,3) ,所以函数在处取得极值。故
M( 51, 3
).N(3, 9 )
(Ⅰ) 直线 MP 的方程为
2 24 5 4 .3 3
m m m my x
由
2 2
3 2
4 5 4
3 3
1 33
m m m my x
y x x x
得 3 2 2 23 ( 4 4) 4 0x x m m x m m
线段 MP 与曲线 ( )f x 有异于 M,P 的公共点等价于上述方程在(-1,m)上有根,即函数
3 2 2 2( ) 3 ( 4 4) 4g x x x m m x m m 在(-1,m)上有零点.
因为函数 ( )g x 为三次函数,所以 ( )g x 至多有三个零点,两个极值点.
又 ( 1) ( ) 0g g m .因此, ( )g x 在 ( 1, )m 上有零点等价于 ( )g x 在 ( 1, )m 内恰有一个极大值点和一个极小
值点,即 2 2'( ) 3 6 ( 4 4) 0 (1, )g x x x m m m 在 内有两不相等的实数根.
等价于
2
2 2
2 2
36 12 4 4 0
3( 1) 6 ( 4 4) 0
3 6 ( 4 4) 0
1
m m
m m
m m m m
m
= ( )>
即
1 5
2 1, 2 5
1
m
m m m
m
或 解得
又因为 1 3m ,所以 m 的取值范围为(2,3)
从而满足题设条件的 r 的最小值为 2.
106.(2009 辽宁卷文)(本小题满分 12 分)
设 2( ) ( 1)xf x e ax x ,且曲线 y=f(x)在 x=1 处的切线与 x 轴平行。
(2)求 a 的值,并讨论 f(x)的单调性;
(1)证明:当 [0, ] f(cos ) f(sin ) 22
时,
解析 (Ⅰ) 2'( ) ( 1 2 1)xf x e ax x ax .有条件知,
'(1) 0f ,故 3 2 0 1a a a . ………2 分
于是 2'( ) ( 2) ( 2)( 1)x xf x e x x e x x .
故当 ( , 2) (1, )x 时, '( )f x <0;
当 ( 2,1)x 时, '( )f x >0.
从而 ( )f x 在 ( , 2) , (1, ) 单调减少,在 ( 2,1) 单调增加. ………6 分
(Ⅱ)由(Ⅰ)知 ( )f x 在[0,1] 单调增加,故 ( )f x 在[0,1] 的最大值为 (1)f e ,
最小值为 (0) 1f .
从而对任意 1x , 2x [0,1] ,有 1 2( ) ( ) 1 2f x f x e . ………10 分
而当 [0, ]2
时, cos ,sin [0,1] .
从而 (cos ) (sin ) 2f f ………12 分
107.(2009 辽宁卷理)(本小题满分 12 分)
已知函数 f(x)=
2
1 x 2 -ax+(a-1) ln x , 1a 。
(1)讨论函数 ( )f x 的单调性;
(2)证明:若 5a ,则对任意 x 1 ,x 2 (0, ) ,x 1 x 2 ,有 1 2
1 2
( ) ( ) 1f x f x
x x
。
解析 (1) ( )f x 的定义域为 (0, ) 。
2
' 1 1 ( 1)( 1 )( ) a x ax a x x af x x a x x x
2 分
(i)若 1 1a 即 2a ,则
2
' ( 1)( ) xf x x
故 ( )f x 在 (0, ) 单调增加。
(ii)若 1 1a ,而 1a ,故1 2a ,则当 ( 1,1)x a 时, ' ( ) 0f x ;
当 (0, 1)x a 及 (1, )x 时, ' ( ) 0f x
故 ( )f x 在 ( 1,1)a 单调减少,在 (0, 1),(1, )a 单调增加。
(iii)若 1 1a ,即 2a ,同理可得 ( )f x 在 (1, 1)a 单调减少,在 (0,1),( 1, )a 单调增加.
(II)考虑函数 ( ) ( )g x f x x
21 ( 1)ln2 x ax a x x
则 21 1( ) ( 1) 2 ( 1) 1 ( 1 1)a ag x x a x a ax x
g
由于 11,证明对任意的 c,都有 M>2:
(Ⅲ)若 M≧K 对任意的 b、c 恒成立,试求 k 的最大值。
本小题主要考察函数、函数的导数和不等式等基础知识,考察综合运用数学知识进行推理
论证的能力和份额类讨论的思想(满分 14 分)
(I)解析 2'( ) 2f x x bx c ,由 ( )f x 在 1x 处有极值 4
3
可得
'(1) 1 2 0
1 4(1) 3 3
f b c
f b c bc
解得 1 ,1
b
c
或 1
3
b
c
若 1, 1b c ,则 2 2'( ) 2 1 ( 1) 0f x x x x ,此时 ( )f x 没有极值;
若 1, 3b c ,则 2'( ) 2 3 ( 1)( 1)f x x x x x
当 x 变化时, ( )f x , '( )f x 的变化情况如下表:
x ( , 3) 3 ( 3,1) 1 (1, )
'( )f x 0 + 0
( )f x 极小值 12 极大值 4
3
当 1x 时, ( )f x 有极大值 4
3
,故 1b , 3c 即为所求。
(Ⅱ)证法 1: 2 2( ) | '( ) | | ( ) |g x f x x b b c
当| | 1b 时,函数 '( )y f x 的对称轴 x b 位于区间[ 1.1] 之外。
'( )f x 在[ 1,1] 上的最值在两端点处取得
故 M 应是 ( 1)g 和 (1)g 中较大的一个
2 (1) ( 1) | 1 2 | | 1 2 | | 4 | 4,M g g b c b c b 即 2M
证法 2(反证法):因为| | 1b ,所以函数 '( )y f x 的对称轴 x b 位于区间[ 1,1] 之外,
'( )f x 在[ 1,1] 上的最值在两端点处取得。
故 M 应是 ( 1)g 和 (1)g 中较大的一个
假设 2M ,则
( 1) | 1 2 | 2
(1) | 1 2 | 2
g b c
g b c
将上述两式相加得:
4 | 1 2 | | 1 2 | 4 | | 4b c b c b ,导致矛盾, 2M
(Ⅲ)解法 1: 2 2( ) | '( ) | | ( ) |g x f x x b b c
(1)当| | 1b 时,由(Ⅱ)可知 2M ;
(2)当| | 1b 时,函数 '(y f x )的对称轴 x b 位于区间[ 1,1] 内,
此时 max ( 1), (1), ( )M g g g b
由 '(1) '( 1) 4 ,f f b 有 2'( ) '( 1) ( 1) 0f b f b
①若 1 0,b 则 '(1) '( 1) '( ), ( 1) max (1), ( )f f f b g g g b ,
于是 21 1 1 1max | '(1),| '( ) | (| '(1) | '( ) |) | '(1) '( ) | ( 1)2 2 2 2M f f b f f b f f b b
②若 0 1b ,则 '( 1) '(1) '( ),f f f b (1) max ( 1), ( )g g g b
于是 21 1 1 1max | '( 1) |,| '( ) | (| '( 1) | | '( ) |) | '( 1) '( ) | ( 1)2 2 2 2M f f b f f b f f b b
综上,对任意的b 、 c 都有 1
2M
而当 10, 2b c 时, 2 1( ) 2g x x 在区间[ 1,1] 上的最大值 1
2M
故 M k 对任意的b 、 c 恒成立的 k 的最大值为 1
2
。
解法 2: 2 2( ) | '( ) | | ( ) |g x f x x b b c
(1)当| | 1b 时,由(Ⅱ)可知 2M ;
(2)当| | 1b 时,函数 '( )y f x 的对称轴 x b 位于区间[ 1,1] 内,
此时 max ( 1), (1), ( )M g g g b
24 ( 1) (1) 2 ( ) | 1 2 | | 1 2 | 2 | |M g g g h b c b c b c
2 2| 1 2 ( 1 2 ) 2( ) | | 2 2 | 2b c b c b c b ,即 1
2M
下同解法 1
113.(2009 宁夏海南卷文)(本小题满分 12 分)
已知函数 3 2 2 3( ) 3 9f x x ax a x a .
设 1a ,求函数 f x 的极值;
若 1
4a ,且当 1,4x a 时, )(' xf 12a 恒成立,试确定 a 的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分。作答时用 2B
铅笔在答题卡上把所选题目对应的题号涂黑。
(21)解析
(Ⅰ)当 a=1 时,对函数 ( )f x 求导数,得
' 2( ) 3 6 9.f x x x
令 '
1 2( ) 0, 1, 3.f x x x 解得
列表讨论 '( ), ( )f x f x 的变化情况:
x ( , 1) 1 (-1,3) 3 (3, )
' ( )f x + 0 — 0 +
( )f x
极大值 6
极小值-26
所以, ( )f x 的极大值是 ( 1) 6f ,极小值是 (3) 26.f
(Ⅱ) ' 2 2( ) 3 6 9f x x ax a 的图像是一条开口向上的抛物线,关于 x=a 对称.
若 '1 1, ( )4 a f x 则 在[1,4a]上是增函数,从而
' ( )f x 在[1,4a]上的最小值是 ' 2(1) 3 6 9 ,f a a 最大值是 ' 2(4 ) 15 .f a a
由 ' 2 2| ( ) | 12 , 12 3 6 9 12 ,f x a a x ax a a 得 于是有
' 2 ' 2(1) 3 6 9 12 , (4 ) 15 12 .f a a a f a a a 且
由 ' '1 4(1) 12 1, (4 ) 12 0 .3 5f a a f a a a 得 由 得
所以 1 1 4 1 4( ,1] [ ,1] [0, ], ( , ].4 3 5 4 5a a 即
若 a>1,则 ' 2 '| ( ) | 12 12 . [1,4 ] | ( ) | 12f a a a x a f x a 故当 时 不恒成立.
所以使 '| ( ) | 12 ( [1,4 ])f x a x a 恒成立的 a 的取值范围是 1 4( , ].4 5
114.(2009 天津卷理)(本小题满分 12 分)
已知函数 2 2( ) ( 2 3 ) ( ),xf x x ax a a e x R 其中 a R
(1)当 0a 时,求曲线 ( ) (1, (1))y f x f 在点 处的切线的斜率;
(2)当 2
3a 时,求函数 ( )f x 的单调区间与极值。
本小题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算
能力及分类讨论的思想方法。满分 12 分。
(I)解析 .3)1(')2()(')(0 22 efexxxfexxfa xx ,故,时,当
.3))1(,1()( efxfy 处的切线的斜率为在点所以曲线
(II) .42)2()(' 22 xeaaxaxxf 解:
.223
2.220)(' aaaaxaxxf 知,由,或,解得令
以下分两种情况讨论。
(1) a若 >
3
2 ,则 a2 < 2a .当 x 变化时, )()(' xfxf , 的变化情况如下表:
x a2 , a2 22 aa, 2a ,2a
+ 0 — 0 +
↗ 极大值 ↘ 极小值 ↗
.)22()2()2()( 内是减函数,内是增函数,在,,,在所以 aaaaxf
.3)2()2(2)( 2aaeafafaxxf ,且处取得极大值在函数
.)34()2()2(2)( 2 aeaafafaxxf ,且处取得极小值在函数
(2) a若 <
3
2 ,则 a2 > 2a ,当 x 变化时, )()(' xfxf , 的变化情况如下表:
x 2 a, 2a aa 22 , a2 ,a2
+ 0 — 0 +
↗ 极大值 ↘ 极小值 ↗
内是减函数。,内是增函数,在,,,在所以 )22()2()2()( aaaaxf
.)34()2()2(2)( 2 aeaafafaxxf ,且处取得极大值在函数
.3)2()2(2)( 2aaeafafaxxf ,且处取得极小值在函数
115.(2009 四川卷理)(本小题满分 12 分)
已知 0, 1a a 且 函数 ( ) log (1 )x
af x a 。
(I)求函数 ( )f x 的定义域,并判断 ( )f x 的单调性;
(II)若
( )
*, lim ;
f n
nn
an N a a
求
(III)当 a e ( e 为自然对数的底数)时,设 ( ) 2( ) (1 )( 1)f xh x e x m ,若函数 ( )h x 的极值存在,
求实数 m 的取值范围以及函数 ( )h x 的极值。
本小题主要考查函数、数列的极限、导数应用等基础知识、考查分类整合思想、推理和运算能力。
解析 (Ⅰ)由题意知1 0xa
当 0 1 ( ) 0 1 ( ) 0a f x a f x 时, 的定义域是( , );当 时, 的定义域是( ,)
ln log1 1a
a e g
x x
x x
-a af (x)= a a
当 0 1 (0, ). 1 0, 0,x xa x a a 时, 因为 故f (x)<0,所以f(x)是减函数
当 1 ( ,0), 1 0, 0, ( ) 0, ( )x xa x a a f x f x 时, 因为 故 所以 是减函数 ….(4 分)
(Ⅱ)因为 ( )( ) log (1 ), 1n f n n
af n a a a 所以
由函数定义域知1 na >0,因为 n 是正整数,故 01时,g (x)>0在R上恒成立,
故函数g(x)在R上为增函数
(2)当 4 4 0,k 即当k=1时,
2
2 2
( 1)( ) 0( 0)( )
xe xg x xx k
K=1 时,g(x)在 R 上为增函数
(3) 4 4 0,k 即当04×240×240
9 m1m2<9×160×160 所以 1 2 1 2
1 2 1 2
4(400 )(400 ) 9 0(400 )(400 )
m m m m
m m m m
,
所以 1 2 1 2
2 1
1 2 1 2
4(400 )(400 ) 9( ) 0(400 )(400 )
m m m mm m m m m m
即 1 2y y 函数 4 9
400y m m
在(0,160)上为减函数.
同理,函数 4 9
400y m m
在(160,400)上为增函数,设 1609×160×160
所以 1 2 1 2
1 2 1 2
4(400 )(400 ) 9 0(400 )(400 )
m m m m
m m m m
,
所以 1 2 1 2
2 1
1 2 1 2
4(400 )(400 ) 9( ) 0(400 )(400 )
m m m mm m m m m m
即 1 2y y 函数 4 9
400y m m
在(160,400)上为增函
数.
所以当 m=160 即 4 10x 时取”=”,函数 y 有最小值,
所以弧 上存在一点,当 4 10x 时使建在此处的垃圾处理厂对城 A 和城 B 的总影响度最小.
【命题立意】:本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的 能力和运用换
元法和基本不等式研究函数的单调性等问题.
120. (2009 湖南卷理)(本小题满分 13 分)
某地建一座桥,两端的桥墩已建好,这两墩相距 m 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经
预测,一个桥墩的工程费用为 256 万元,距离为 x 米的相邻两墩之间的桥面工程费用为 (2 )x x 万元。
假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 y 万元。
(Ⅰ)试写出 y 关于 x 的函数关系式;
(Ⅱ)当 m =640 米时,需新建多少个桥墩才能使 y 最小?
解 (Ⅰ)设需要新建 n 个桥墩, ( 1) 1mn x m x
,即n=
所以 (2 )m mx x xx x
y=f(x)=256n+(n+1)(2+ )x=256( -1)+
256 2 256.x m x mx
(Ⅱ) 由(Ⅰ)知, 2
3 3
2 2
2
256 1'( ) ( 512).2 2
m mf x mx xxx
令 '( ) 0f x ,得 3
2 512x ,所以 x =64
当 0< x <64 时 '( )f x <0, ( )f x 在区间(0,64)内为减函数;
当 64 640x 时, '( )f x >0. ( )f x 在区间(64,640)内为增函数,
所以 ( )f x 在 x =64 处取得最小值,此时, 6401 1 9.64
mn x
故需新建 9 个桥墩才能使 y 最小。
121.(2009 年上海卷理)有时可用函数
0.1 15ln ,( 6)
( ) 4.4 ,( 6)4
a xa xf x x xx
描述学习某学科知识的掌握程度,其中 x 表示某学科知识的学习次数( *x N ), ( )f x 表示对该学科知
识的掌握程度,正实数 a 与学科知识有关。
(1)证明 当 7x 时,掌握程度的增加量 ( 1) ( )f x f x 总是下降;
(2)根据经验,学科甲、乙、丙对应的 a 的取值区间分别为
(115,121], (121,127], (121,133] 。当学习某学科知识 6 次时,掌握程度是 85%,请确定相应的学科。
证明 (1)当 0.47 ( 1) ( ) ( 3)( 4)x f x f x x x
时,
而当 7x 时 ,函数 ( 3)( 4)y x x 单调递增,且 ( 3)( 4)x x >0……..3 分
故 ( 1) ( )f x f x 单调递减
当 7x 时 ,掌握程度的增长量 ( 1) ( )f x f x 总是下降……………..6 分
(2)由题意可知 0.1+15ln
6
a
a =0.85……………….9 分
整理得 0.05
6
a ea
解得
0.05
0.05 6 20.50 6 123.0,123.0 (121,127]1
ea e
…….13 分
由此可知,该学科是乙学科……………..14 分
122.(2009 上海卷文)(本题满分 16 分)本题共有 2 个小题,第 1 小题满分 6 分,第 2 小题满分 10 分 .
有时可用函数
0.1 15ln , 6,
( ) 4.4 , 64
a xa xf x x
x
描述学习某学科知识的掌握程度.其中 x 表示某学科知识的学习次数( *x N ), ( )f x 表示对该学科知识
的掌握程度,正实数 a 与学科知识有关.
(1)证明:当 x 7 时,掌握程度的增长量 f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的 a 的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识 6 次时,掌握程度是 85%,请确定相应的学科.
证明 (1)当 7x 时, 0.4( 1) ( ) ( 3)( 4)f x f x x x
而当 7x 时,函数 ( 3)( 4)y x x 单调递增,且 ( 3)( 4) 0x x
故函数 ( 1) ( )f x f x 单调递减
当 7x 时,掌握程度的增长量 ( 1) ( )f x f x 总是下降
(2)有题意可知 0.1 15ln 0.856
a
a
整理得 0.05
6
a ea
解得
0.05
0.05 6 20.50 6 123.0,123.0 (121,127]1
ea e
…….13 分
由此可知,该学科是乙学科……………..14 分
第二部分 两年模拟题
2010 年模拟题
题组一
一、选择题
1.(安徽省百校论坛 2011 届高三第三次联合考试理)设 ( )f x 是定义在 R 上的偶函数,对任意 x R ,都
有 ( 2) ( 2),f x f x 且当
[ 2,0]x 时, 1( ) ( ) 1, ( 2,6]2
xf x 若在区间 内关于 x 的方程
( ) log ( 2) 0( 1)af x x a 恰有 3 个不同的实数根,则 a 的取值范围是 ( )
A.(1,2) B. (2, ) C. 3(1, 4) D. 3( 4,2)
答案 D.
2.(山东省莱阳市 2011 届高三上学期期末数学模拟理)函数 ( ) ( 3) xf x x e 的单调递增区间是( )
A. ( ,2) B. (0,3) C. (1,4) D. (2, )
答案:D.
3.(河南省辉县市第一高级中学 2011 届高三 12 月月考理)下列命题中是假命题的是
A. ,)1()(, 342 是幂函数使 mmxmxfm R ),0( 且在 上递减
B. 有零点函数 axxxfa lnln)(,0 2
C. sincos)cos(,, 使R ;
D. , ( ) sin(2 )f x x R 函数 都不是偶函数
答案 D.
4.(河南省焦作市部分学校 2011 届高三上学期期终调研测试理)已知函数 ,
下面结论错误的是
A.函数 的最小正周期为 B.函数 是奇函数
C.函数 的图象关于直线 对称 D.函数 在区间 上是减函数
答案 D.
5.(河南省鹿邑县五校 2011 届高三 12 月联考理)已知函数 ( ) , ( )f x x g x 是定义在 R 上的偶函数,当 0x
时, ( ) lng x x ,则函数 ( ) ( )y f x g x 的大致图像为 ( )
答案 A.
6、(黑龙江省佳木斯大学附属中学 2011 届高三上学期期末考试理)函数 xexxf )3()( 的单调增区间
是 ( )
A. )2,( B. )3,0( C. )4,1( D. ),2(
答案 D.
7. (江西省吉安一中 2011 届高三第一次周考)将函数 ( ) sin(f x x )的图象向左平移
2
个单位,若
所得图象与原图象重合,则 的值不可能等于
A.4 B.6 C.8 D.12
答案 B.
8.(浙江省诸暨中学 2011 届高三 12 月月考试题文)
已知函数 ),0(cossin)( Rxabaxbxaxf 为常数,、 在
4
x 处取得最小值,
则函数 )4
3( xfy 是
A.偶函数且其图象关于点 0, 对称
B.偶函数且其图象关于点 )0,2
3( 对称
C.奇函数且其图象关于点 )0,2
3( 对称
D.奇函数且其图象关于点 0, 对称
答案 D.
9.(山东省济宁一中 2011 届高三第三次质检理)设 a R ,函数 ( ) x xf x e a e 的导函数 '( )y f x 是
奇函数,若曲线 ( )y f x 的一条切线斜率为 3
2
,则切点的横坐标为 ( )
A. ln 2
2 B. ln 2
2
C. ln 2 D. ln 2
答案 C.
10.(山东省莱阳市 2011 届高三上学期期末数学模拟理)设奇函数 ( )f x 定义在 ( ,0) (0, ) 上, ( )f x
在 (0, ) 上为增函数,且 (1) 0f ,则不等式 3 ( ) 2 ( ) 05
f x f x
x
的解集为( )
A. ( 1,0) (1, ) B. ( , 1) (0,1) C. ( , 1) (1, ) D. ( 1,0) (0,1)
答案:D.
11.(浙江省诸暨中学 2011 届高三 12 月月考试题文)
已知函数 ),0(cossin)( Rxabaxbxaxf 为常数,、 在
4
x 处取得最小值,
则函数 )4
3( xfy 是
A.偶函数且其图象关于点 0, 对称
B.偶函数且其图象关于点 )0,2
3( 对称
C.奇函数且其图象关于点 )0,2
3( 对称
D.奇函数且其图象关于点 0, 对称
答案 D.
12.(山东省聊城市 2011 届高三年级 12 月月考理)函数 sin(2 )3y x 的图象 ( )
A.关于点 ( ,0)3
对称B.关于直线
4x 对称
C.关于点 ( ,0)4
对称 D.关于直线
3x 对称
答案 A.
13.(宁夏银川一中 2011 届高三第五次月考试题全解全析理)
2(sin cos ) 1y x x 是 ( )
A.最小正周期为 2π 的偶函数 B.最小正周期为 2π 的奇函数
C.最小正周期为 π 的偶函数 D.最小正周期为 π 的奇函数
【答案】D
【分析】对给出的三角函数式进行变换,然后根据三角函数的性质进行判断。
【解析】 2(sin cos ) 1 2sin cos sin 2y x x x x x ,所以函数 2(sin cos ) 1y x x 是最小正周期
为 的奇函数。
【考点】基本初等函数Ⅱ。
【点评】本题考查三角函数的性质,但要借助三角恒等变换,在大多数三角函数性质的试题中往往要以三
角恒等变换为工具,把三角函数式化为一个角的一个三角函数,再根据基本的三角函数的性质对所给的三
角函数的性质作出结论。
14.(吉林省东北师大附中 2011 届高三上学期第三次模底考试理)定义两种运算: 22 baba ,
2)( baba ,则
2
2 2
xf x x
是( )函数. ( )
A.奇函数 B.偶函数
C.既奇又偶函数 D.非奇非偶函数
答案 A.
15.(宁夏银川一中 2011 届高三第五次月考试题全解全析理)
把函数 )||,0)(sin( xy 的图象向左平移
6
个单位,再将图像上所有点的横坐标伸长到原来
的 2 倍(纵坐标不变)所得的图象解析式为 xsiny ,则 ( )
A.
62 , B.
32 ,
C.
62
1 , D.
122
1 ,
【答案】B
【分析】根据变换的结果,逆行变换后即可得到 siny x 经过变换后的函数解析式,通过比较即可确定
, 的值。
【解析】把 siny x 图象上所有点的横坐标缩小到原来的 1
2
倍得到的函数解析式是 sin 2y x ,再把这个
函数图象向右平移
6
,得到的函数图象的解析式是 sin 2( ) sin(2 )6 3y x x ,与已知函数比较得
2, 3
。
【考点】基本初等函数Ⅱ。
【点评】本题考查三角函数图象的变换,试题设计成逆向考查的方式是比较有新义的。本题也可以根据比
较系数的方法求解,根据已知的变换方法,经过两次变换后函数 sin( )y x ,即被变换成
sin( )6y x ,比较系数也可以得到问题的答案。
16.(山东省莱阳市 2011 届高三上学期期末数学模拟理)
若函数 2( ) sin 2 2sin sin 2f x x x x ( )x R ,则 ( )f x 是( )
A.最小正周期为 的偶函数
B. 最小正周期为 的奇函数
C.最小正周期为 2 的偶函数
D. 最小正周期为
2
的奇函数
答案:D.
17.(宁夏银川一中 2011 届高三第五次月考试题全解全析理)
设 )(xf Rxxx ,3 ,当 0
2
时, 0)1()sin( mfmf 恒成立,则实数 m 的取值范围是
( )
A.(0,1) B. )0,( C. )2
1,( D. )1,(
【答案】D
【分析】函数 ( )f x 是奇函数且是单调递增的函数,根据这个函数的性质把不等式转化成一个具体的不等
式。根据这个不等式恒成立,
【解析】根据函数的性质,不等式 0)1()sin( mfmf ,即 ( sin ) ( 1)f m f m ,即 sin 1m m
在 0, 2
上恒成立。当 0m 时,即 1sin m
m
恒成立,只要 10 m
m
即可,解得 0 1m ;当 0m
时,不等式恒成立;当 0m 时,只要 1sin m
m
,只要 11 m
m
,只要 0 1 ,这个不等式恒成立,
此时 0m 。综上可知: 1m 。
【考点】基本初等函数Ⅰ。
【点评】本题考查函数性质和不等式的综合运用,这里函数性质是隐含在函数解析式中的,其目的是考查
考生是否有灵活使用函数性质简捷地解决问题的思想意识。在不等式的恒成立问题中要善于使用分类参数
的方法解决问题,本题的解析是分类了函数,把参数放到一个表达式中,也可以直接使用分离参数的方法
求 解 , 即 sin 1m m 可 以 化 为 (1 sin ) 1m , 当
2
时 , mR ; 当
2
时 ,
1 ( )1 sinm f
,只要 min( )m f 即可,即只要 1m 即可。综合两种情况得到 1m 。
18.(四川广安二中 2011 届高三数学一诊复习题综合测试题三)
已知函数 ( ) sin( )( 0, 0)f x A x A 的图象在 y 轴右侧的第一个最高点为 (2,2),M 与 x 轴在原
点右侧的第一个交点为 (5,0),N 则函数 ( )f x 的解析式为
A. 2sin( )6 6x B. 2sin( )3 6x
C. 2sin( )6 6x D. 2sin( )3 6x
答案 A.
19.(浙江省诸暨中学 2011 届高三 12 月月考试题文)已知函数 2 2f x x ax a 在区间 ,1 上有最
小值,则函数 f x
x
在区间 1, 上
A 有两个零点 B 有一个零点 C.无零点 D.无法确定
答案 C.
20.(重庆市南开中学高 2011 级高三 1 月月考文)设 3
6
log ( 1) ( 6)
( )
3 1 ( 6)x
x x
f x
x
的反函数为
1 1 8( ), ( ) ,9f x f n 若 则 ( 4)f n =
( )
A.2 B.—2 C.1 D.—1
答案 B.
21.(北京市西城区 2011 届高三第一学期期末考试理)对于函数① 1( ) 4 5f x x x
,②
2
1( ) log ( )2
xf x x ,③ ( ) cos( 2) cosf x x x ,
判断如下两个命题的真假:
命题甲: ( )f x 在区间 (1,2) 上是增函数;
命题乙: ( )f x 在区间 (0, ) 上恰有两个零点 1 2,x x ,且 1 2 1x x .
能使命题甲、乙均为真的函数的序号是
(A)① (B)② (C)①③ (D)①②
答案 D.
22.(山东省莱阳市 2011 届高三上学期期末数学模拟理)函数
21
4 3
xy x x
是( )
A. 奇函数 B. 偶函数 C. 非奇非偶函数 D. 既是奇函数又是偶函数
答案:B.
23.(重庆市重庆八中 2011 届高三第四次月考文)
若函数 f x 的反函数 1 21 0f x x x ,则 2f ( )
A.1 B. 1 C.1 或 1 D.5
答案 B.
24.(广东六校 2011 届高三 12 月联考文) 下列函数中,既是偶函数又在 0, 上单调递增的是
A. 3y x B. cosy x C. xy tan D. lny x
答案 D.
25.(宁夏银川一中 2011 届高三第五次月考试题全解全析理)
a 是 xxf x
2
1log2)( 的零点,若 ax 00 ,则 )( 0xf 的值满足 ( )
A. 0)( 0 xf B. 0)( 0 xf C. 0)( 0 xf D. )( 0xf 的符号不确定
【答案】B
【分析】函数 2( ) 2 logxf x x 在 (0, ) 上是单调递增的,这个函数有零点,这个零点是唯一的,根据
函数是单调递增性,在 (0, )a 上这个函数的函数值小于零,即 0( ) 0f x 。
【考点】函数的应用。
【点评】在定义域上单调的函数如果有零点,则只能有唯一的零点,并且以这个零点为分界点把定义域分
成两个区间,在其中一个区间内函数值都大于零,在另一个区间内函数值都小于零。
26.(重庆市重庆八中 2011 届高三第四次月考文)函数 2 6f x ax bx 满足条件 1 3f f ,则 2f
的值为 ( )
A .5 B .6 C .8 D .与 a ,b 值有关
答案 B 提示:由 1 3f f 知对称轴 12
b
a ,故 2 2 6f x ax ax ,所以 2 6f .
27.(重庆市重庆八中 2011 届高三第四次月考文)函数 2 2f x x ax a 在 ,1x 上有最小值,则函
数 f xg x x 在 1,x 上一定 ( )
A .有最小值 B .有最大值 C .是减函数 D .是增函数
答案: D 提示:由函数 2 2f x x ax a 在 ,1 有最小值,
知 1a ,又 2ag x x ax ,由 1x 及 1a 知
2
2 2' 1 a x ag x
x x
2
1 0a
x
,故 g x 为增函数.
28.(安徽省百校论坛 2011 届高三第三次联合考试理)
已知函数 2
2 1, 1,( ) [ (0)] 4
, 1,
x xf x f f a
x ax x
若 ,则实数 a 等于 ( )
A. 1
2 B. 4
5 C.2 D.9
答案 C.
29.(安徽省蚌埠二中 2011 届高三第二次质检文)
已知函数 )10()3(log)( 2 aaaxxxf a 且 满足:对任意实数 x1、x2,当
221
axx
时,总有 0)()( 21 xfxf ,那么实数 a 的取值范围是 ( )
A.(0,3) B.(1,3) C. )32,1( D. )32,0(
答案 C.
30. ( 福建 省 莆 田一 中 2011 届 高三 上 学 期第 三 次 月考 试 题文 ) 已 知函 数
)0,0)(sin(2)( xxf 的图象如图所示,则 等于( )
A. 1
3 B.
3
2 C. 1 D.2
答案 B.
31.(福建省莆田一中 2011 届高三上学期第三次月考试题文)函数 )(xf 在定义域
R 内可导,若 ( ) (2 ),f x f x 且 ( 1) '( ) 0x f x ,若 ),3(),2
1(),0( fcfbfa 则 cba ,, 的大小关
系是( )
A. cba B.b a c C. abc D. bca
答案 B.
32.(宁夏银川一中 2011 届高三第五次月考试题全解全析理)
求曲线 2y x 与 y x 所围成图形的面积,其中正确的是 ( )
A. 1 2
0
( )S x x dx B. 1 2
0
( )S x x dx
C. 1 2
0
( )S y y dy D. 1
0
( )S y y dy
【答案】B
【分析】根据定积分的几何意义,确定积分限和被积函数。
【解析】两函数图象的交点坐标是 (0,0),(1,1) ,故积分上限是1,下限是 0 ,由于在 0,1 上, 2x x ,故
求曲线 2y x 与 y x 所围成图形的面 1 2
0
( )S x x dx 。
【考点】导数及其应用。
【点评】本题考查定积分的几何意义,对定积分高考可能考查的主要问题是:利用微积分基本定理计算定
积分和使用定积分的几何意义求曲边形的面积。
33.(江西省南昌市新建二中、莲塘一中 2011 届高三上学期 12 月联考理)
函数 1 ln( 1) ,( 1)2
xy x 的反函数是( )
A. 2 1 1( 0)xy e x B. 2 1 1( 0)xy e x
C. 2 1 1( R)xy e x D. 2 1 1( R)xy e x
答案 D.
34.(安徽省蚌埠二中 2011 届高三第二次质检文)
已知函数 aaxxxf 2)( 2 在区间( ,1)上有最小值,则函数
x
xfxg )()( 在区间
(1, ) 上一定 ( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
答案 D.
35.(北京市房山区 2011 年高三上学期期末统练试卷文)阅 读右面程序框图,
如果输出的函数值在区间 1 1[ , ]4 2
内,那么输入实数 x 的取 值范围是
(A) ( , 2]
(B)[ 2, 1]
(C)[ 1,2]
(D)[2, )
开始
输出
结束
是
否
输入 x
[ 2,2]x
( ) 2xf x
( )f x
( ) 2f x
答案 B.
二、填空题
36.(四川广安二中 2011 届高三数学一诊复习题综合测试题三)在 ABC 中,已知 , ,a b c 是角 , ,A B C
的对应边,
①若 ,a b 则 ( ) (sin sin )f x A B x 在R上是增函数;
②若 2 2 2( cos cos )a b a B b A ,则 ABC 是 Rt ; ③ cos sinC C 的最小值为
2 ;
④若 cos cosA B ,则A=B;
⑤若 (1 tan )(1 tan ) 2A B ,则 3
4A B ,其中正确命题的序号是 。
答案 ①②④
37.(苏北九所重点高中 2011 届高三期末联考试卷试题)函数 2cosy x x 在[0, ]2
上取最大值时,x 的
值是__▲____.
答案
6
;
38.(苏北九所重点高中 2011 届高三期末联考试卷试题)已知函数 2( ) logf x x ,正实数 m,n 满足 m n ,
且 ( ) ( )f m f n ,
若 ( )f x 在区间 2[ , ]m n 上的最大值为 2,则 n m ▲
答案 5
2
;
39. ( 安 徽 省 蚌 埠 二 中 2011 届 高 三 第 二 次 质 检 文 ) 设 奇 函 数 ]1,1[)( 在xf 上 是 增 函 数 , 且
12)(,1)1( 2 attxff 若函数 对 所 有 的 ]1,1[a , ]1,1[x 都 成 立 , 则 t 的 取 值 范 围 是
____________________________,
答案 202 ttt 或或
40.(福建省莆田一中 2011 届高三上学期第三次月考试题文)
已知函数 )(|2|)( 2 Rxbaxxxf .给下列命题:① )(xf 必是偶函数;②当 )2()0( ff 时, )(xf
的图像必关于直线 x=1 对称;③若 02 ba ,则 )(xf 在区间
[a,+∞ ) 上是增函数;④ )(xf 有最大值 || 2 ba .其中正确的序号是_________.
答案 ③
41.(福建省莆田一中 2011 届高三上学期期中试题理) )(xf 是定义在 R 上的奇函数,且 )1()( xfxf ,
则 )2010(f .
答案 0
42.(湖北省八校 2011 届高三第一次联考理)奇函数 ( )f x 满足对任意 x R 都有 (2 ) (2 ) 0f x f x ,
且 (1) 9f ,则
(2010) (2011) (2012)f f f 的值为 .
答案 9 .
43 .( 江 苏 连 云 港 市 2011 届 高 三 一 轮 复 习 模 拟 考 试 试 题 ) 函 数 2lg( 4 21)y x x 的 定 义 域 是
★ .
答案 21、 ( , 3) ∪ (7, ) .
43.(湖北省补习学校 2011 届高三联合体大联考试题理)若 ( )f x 是 R 上的奇函数,且 (2 1)f x 的周期为 4,
若 2)6( f ,则 (2008) (2010)f f
答案 2.
45.(山东省聊城市 2011 届高三年级 12 月月考理)
定义在 R 上的偶函数 ( ) ( 1) ( ),f x f x f x 满足 且 在[—1,0]上是增函数,给出下列关于 ( )f x 的判断;
① ( )f x 是周期函数;
② ( )f x 关于直线 1x 对称;
③ ( )f x 是[0,1]上是增函数;
④ ( )f x 在[1,2]上是减函数;
⑤ (2) (0)f f ,
其中正确的序号是 。
答案 ①②⑤.
46 .( 浙 江 省 诸 暨 中 学 2011 届 高 三 12 月 月 考 试 题 文 )( 本 小 题 满 分 14 分 ) 已 知 : 函 数
( ) 2(sin cos )f x x x .
(Ⅰ)求函数 ( )f x 的最小正周期和值域;
(Ⅱ)若函数 ( )f x 的图象过点 6( , )5
, 3
4 4
.求 ( )4f 的值.
答案 (1)(1) ( ) 2(sin cos )f x x x 2 22(sin cos )2 2x x 2sin( )4x ---3 分
∴函数的最小正周期为 2 ,值域为{ | 2 2}y y 。
(2)解:依题意得: 62sin( ) ,4 5
3sin( ) ,4 5
∵ 3 .4 4
∴ 0 ,4 2
∴ cos( )4
= 2 23 41 sin ( ) 1 ( )4 5 5
( )4f = 2sin[( ) ]4 4
∵sin[( ) ] sin( )cos cos( )sin4 4 4 4 4 4
= 2 3 4 7 2( )2 5 5 10
∴ ( )4f = 7 2
5
.
47.(安徽省合肥八中 2011 届高三第一轮复习四考试理)
已知函数 3( ) 2 '(2) , '(2),f x x f x n f 则二项式
2( )nx
x
展开式中常数项是第 项。
答案: 9.
48.(安徽省百校论坛 2011 届高三第三次联合考试理)
已知 ( ) 2sin(2 ) [0, ]6 2f x x m x 在 上有两个不同的零点,则 m 的取值范围为 。
答案
三、简答题
49.(四川广安二中 2011 届高三数学一诊复习题综合测试题三)(12 分)已知函数 ( ) sin( ),f x x 其
中 0,| | .2
(1)若 3cos cos sin sin 0,4 4
求 的值;
(2)在(1)的条件下,若函数 ( )f x 的图象的相邻两条对称轴之间的距离等于 ,3
求最小的正实数 ,m 使得函
数的图象向左平移 m 个单位后所对应的函数是偶函数。
答案 (1) 3cos cos sin sin 0 0 cos cos sin sin cos( )4 4 4 4 4
又| | 2
;4
∴
(2)由题意知,
2 3
T 2
3T ∴ 2 3T
∴ ( ) sin(3 )4f x x ∴
又 ( ) sin(3 3 )4f x m x m 是偶函数, 3 0 3 ( Z)4 2m k k ∴
即 ( Z)3 12
km k 所以,最小的正实数 m 是 .12
50.(本小题满分 14 分)已知:函数 ( ) 2(sin cos )f x x x .
(Ⅰ)求函数 ( )f x 的最小正周期和值域;
(Ⅱ)若函数 ( )f x 的图象过点 6( , )5
, 3
4 4
.求 ( )4f 的值.
答案 (1)(1) ( ) 2(sin cos )f x x x 2 22(sin cos )2 2x x 2sin( )4x ---3 分
∴函数的最小正周期为 2 ,值域为{ | 2 2}y y 。
(2)解:依题意得: 62sin( ) ,4 5
3sin( ) ,4 5
∵ 3 .4 4
∴ 0 ,4 2
∴ cos( )4
= 2 23 41 sin ( ) 1 ( )4 5 5
( )4f = 2sin[( ) ]4 4
∵sin[( ) ] sin( )cos cos( )sin4 4 4 4 4 4
= 2 3 4 7 2( )2 5 5 10
∴ ( )4f = 7 2
5
51.(重庆市南开中学高 2011 级高三 1 月月考文)(13 分)
已知向量 1(1,cos ), ( sin )4a x b x
(1)当 [0, ]4x 时,若 a b ,求 x 的值;
(2)定义函数 ( ) ( ), , ( )f x a a b x R f x 求 的最小正周期及最大值。
答案
52 .( 安 徽 省 野 寨 中 学 、 岳 西 中 学 2011 届 高 三 上 学 期 联 考 文 )( 本 题 满 分 12 分 ) 已 知 函 数
3 2( ) 3 ( 0)f x x ax bx c b= + + + < ,且 ( ) ( ) 2g x f x= - 是奇函数。
(1)求 ,a c 的值;
(2)求函数 ( )f x 的单调区间。
答案
53.(广东省高州市南塘中学 2011 届高三上学期 16 周抽考理)(本小题满分 13 分)已知函数
2( ) ( 0 ).af x x x a Rx
,常数
(Ⅰ)当 2a 时,解不等式 ( ) ( 1)f x f x > 2 1x ;
(Ⅱ)讨论函数 ( )f x 的奇偶性,并说明理由.
答案 解:(Ⅰ)当 2a 时, 2 2( )f x x x
, 2 2( 1) ( 1) 1f x x x
,
由 2 22 2( 1) 1x xx x
> 2 1x ,
得 2 2
1x x
> 0 , ( 1)x x < 0 ,0 < x <1
∴原不等式的解为 0 < x <1;
(Ⅱ) ( )f x 的定义域为 ( 0) (0 , ,+ ),
当 0a 时, 2( )f x x , 2 2( ) ( ) ( )f x x x f x ,所以 ( )f x 是偶函数.
当 0a 时, 2( ) ( ) 2 0( 0)f x f x x x , 2( ) ( ) 0af x f x x
所以 ( )f x 既不是奇函数,也不是偶函数.
54.(黑龙江省哈九中 2011 届高三期末考试试题理)(12 分)已知函数 )()( Rxkxexf x
(1)若 ek ,试确定函数 )(xf 的单调区间;
(2)若 0k 且对任意 Rx , 0|)(| xf 恒成立,试确定实数 k 的取值范围;
(3)设函数 )()()( xfxfxF ,求证: )()2()()2()1( 21 NnenFFF
n
n
答案 (1) eexf x )( ,令 0)( xf ,解得 1x
当 ),1( x 时, 0)( xf , )(xf 在 ),1( 单调递增;
当 )1,(x 时, 0)( xf , )(xf 在 ),1( 单调递减
(2) |)(| xf 为偶函数, 0|)(| xf 恒成立等价于 0)( xf 对 0x 恒成立
当 0x 时, kexf x )( ,令 0)( xf ,解得 kx ln
(1)当 0ln k ,即 1k 时, )(xf 在 )ln,0( k 减,在 ),(ln k 增
0ln)(ln)( min kklkkfxf ,解得 ek 1 , ek 1
(2)当 0ln k ,即 10 k 时, 0)( kexf x , )(xf 在 ),0[ 上单调递增,
01)0()( min fxf ,符合, 10 k
综上, ek 0
(3) nnxx eenFeeFeexF )(,)1(,)( 1
2)()1( 11111 nnnnn eeeeenFF
2)1()2( 11221 nnnnn eeeeenFF
。。。。。。
2)1()( 1 neFnF
21 )2()()2()1(
n
nenFFF
55.(湖北省八校 2011 届高三第一次联考理)
(本小题满分12 分)已知 4
2 2
1( ) log (1 ) 1
mxf x x x
( )x R 是偶函数.
(Ⅰ)求实常数 m 的值,并给出函数 ( )f x 的单调区间(不要求证明);
(Ⅱ) k 为实常数,解关于 x 的不等式: ( ) (3 1)f x k f x .
答案 (Ⅰ) ( )f x 是偶函数, ( ) ( )f x f x ,
4 4
2 22 2
1 1log (1 ) log (1 )1 1
mx mxx xx x
,
0mx , 0m . 2 分
4
2 2
1( ) log (1 ) 1f x x x
, ( )f x 的递增区间为[0, ) ,递减区间为 ( ,0] .
4 分
(Ⅱ) ( )f x 是偶函数 , ( ) ( )f x k f x k ,
不等式即 ( ) ( 3 1)f x k f x ,由于 ( )f x 在[0, ) 上是增函数,
3 1x k x , 2 2 22 9 6 1x kx k x x ,
即 2 28 (6 2 ) (1 ) 0x k x k , 1 1( )( ) 02 4
k kx x , 7 分
1 1 3 1( )2 4 4
k k k ,
1
3k 时,不等式解集为 ;
1
3k 时,不等式解集为 1 1( , )4 2
k k ;
1
3k 时,不等式解集为 1 1( , )2 4
k k . 12 分
56.(安徽省百校论坛 2011 届高三第三次联合考试理)
(本小题满分 13 分)
已 知 函 数 2 2( ) ln ( 0, )f x x a x x ax
为常数 , 对 任 意 两 个 不 相 等 的 正 数 1 2,x x , 证 明 : 当
1 2 1 2( ) ( )0 , ( ).2 2
f x f x x xa f 时
答案
57.(安徽省百校论坛 2011 届高三第三次联合考试理)
(本小题满分 13 分)
已知函数 3 2( ) ( 6 3 ) , .xf x x x x t e t R
(1)若函数 ( ) , , ( )y f x x a x b x c a b c 依次在 处取到极值,求 t 的取值范围;
(2)若存在实数 [0,2]t ,使对任意的 [1, ], ( )x m f x x 不等式 恒成立,求正整数 m 的最大值。
答案
58.(安徽省野寨中学、岳西中学 2011 届高三上学期联考文) (本题满分 13 分)设实数 0a < , 设函数
2( ) 1 1 1f x a x x x= - + + + - 的最大值为 ( )g a 。
(1)设 1 1t x x= + + - ,求t 的取值范围,并把 ( )f x 表示为t 的函数 ( )h t ;
(2)求 ( )g a 。
答案 解:(1)因为 [ ]1 1 2,2t x x= + + - Î , 2 211 12x t- = -
所以 [ ]21( ) , 2,22h t at t a t= + - Î
(2)直 1t a= - 线是抛物线 [ ]21( ) , 2,22h t at t a t= + - Î 的对称轴,又 0a <
所以,当 ( ]1 0, 2t a= - Î ,即 2
2a £ - ,则 ( ) ( 2) 2g a h= = ;
当 ( ]1 2,2t a= - Î ,即 2 1
2 2a- < £ - ,则 1 1( ) ( ) 2g a h aa a= - = - - ;
当 ( )1 2,t a= - Î +¥ ,即 2 02 a- < < ,则 ( ) (2) 2g a h a= = +
综上,有
12, 2
1 2 1( ) ,2 2 2
22, 2
a a
g a a aa
a
ìï + > -ïïïïïïï= - - - < £ -íïïïïï £ -ïïïî
59.(北京市西城区 2011 届高三第一学期期末考试理)(本小题满分 13 分)
已知函数 2( ) 3sin 2 2sinf x x x .
(Ⅰ)若点 (1, 3)P 在角 的终边上,求 ( )f 的值;
(Ⅱ)若 [ , ]6 3x ,求 ( )f x 的值域.
答案 (本小题满分 13 分)
解:(Ⅰ)因为点 (1, 3)P 在角 的终边上,
所以 3sin 2
, 1cos 2
, ………………2 分
所以 2 2( ) 3sin 2 2sin 2 3sin cos 2sinf ………………4 分
23 1 32 3 ( ) 2 ( ) 32 2 2
. ………………5 分
(Ⅱ) 2( ) 3sin 2 2sinf x x x 3sin2 cos2 1x x ………………6 分
2sin(2 ) 16x , ………………8 分
因为 [ , ]6 3x ,所以
6
5
626
x , ………………10 分
所以 1 sin(2 ) 12 6x , ………………11 分
所以 ( )f x 的值域是[ 2,1] . ………………13 分
60.(北京市西城区 2011 届高三第一学期期末考试理)(本小题满分 14 分)
已知函数 21( ) (2 1) 2ln ( )2f x ax a x x a R .
(Ⅰ)若曲线 ( )y f x 在 1x 和 3x 处的切线互相平行,求 a 的值;
(Ⅱ)求 ( )f x 的单调区间;
(Ⅲ)设 2( ) 2g x x x ,若对任意 1 (0,2]x ,均存在 2 (0,2]x ,使得 1 2( ) ( )f x g x ,求 a 的取值范围.
答案 (本小题满分 14 分)
解: 2( ) (2 1)f x ax a x
( 0)x . ………………2 分
(Ⅰ) (1) (3)f f ,解得 2
3a . ………………3 分
(Ⅱ) ( 1)( 2)( ) ax xf x x
( 0)x . ………………5 分
①当 0a 时, 0x , 1 0ax ,
在区间 (0,2) 上, ( ) 0f x ;在区间 (2, ) 上 ( ) 0f x ,
故 ( )f x 的单调递增区间是 (0,2) ,单调递减区间是 (2, ) . ………………6 分
②当 10 2a 时, 1 2a
,
在区间 (0,2) 和 1( , )a
上, ( ) 0f x ;在区间 1(2, )a
上 ( ) 0f x ,
故 ( )f x 的单调递增区间是 (0,2) 和 1( , )a
,单调递减区间是 1(2, )a . …………7 分
③当 1
2a 时,
2( 2)( ) 2
xf x x
, 故 ( )f x 的单调递增区间是 (0, ) . ………8 分
④当 1
2a 时, 10 2a
,
在区间 1(0, )a
和 (2, ) 上, ( ) 0f x ;在区间 1( ,2)a
上 ( ) 0f x ,
故 ( )f x 的单调递增区间是 1(0, )a
和 (2, ) ,单调递减区间是 1( ,2)a . ………9 分
(Ⅲ)由已知,在 (0,2] 上有 max max( ) ( )f x g x . ………………10 分
由已知, max( ) 0g x ,由(Ⅱ)可知,
①当 1
2a 时, ( )f x 在 (0,2] 上单调递增,
故 max( ) (2) 2 2(2 1) 2ln 2 2 2 2ln 2f x f a a a ,
所以, 2 2 2ln 2 0a ,解得 ln 2 1a ,故 1ln 2 1 2a . ……………11 分
②当 1
2a 时, ( )f x 在 1(0, ]a
上单调递增,在 1[ ,2]a
上单调递减,
故 max
1 1( ) ( ) 2 2ln2f x f aa a
.
由 1
2a 可知 1 1ln ln ln 12 ea , 2ln 2a , 2ln 2a ,
所以, 2 2ln 0a , max( ) 0f x , ………………13 分
综上所述, ln 2 1a . ………………14 分
61.(安徽省野寨中学、岳西中学 2011 届高三上学期联考文)(本小题满分 12 分)
已知函数 2 π π π( ) 1 2sin ( ) 2sin( )cos( )8 8 8f x x x x .求:
(I)函数 ( )f x 的最小正周期;
(II)函数 ( )f x 的单调增区间。
答案
62 .( 宁 夏 银 川 一 中 2011 届 高 三 第 五 次 月 考 试 题 全 解 全 析 理 )( 本 小 题 满 分 12 分 ) 设 函 数
21( ) ln .2f x x ax bx
(1)当 1
2a b 时,求 )(xf 的最大值;
(2)令 21( ) ( ) 2
aF x f x ax bx x
,( 0 3x ),其图象上任意一点 0 0( , )P x y 处切线的斜率 k ≤ 2
1 恒
成立,求实数 a 的取值范围;
(3)当 0a , 1b ,方程 22 ( )mf x x 有唯一实数解,求正数 m 的值.
【分析】(1)函数的定义域是 (0, ) ,把 1
2a b 代入函数解析式,求其导数,根据求解目标,这个导
数在函数定义域内只有一个等于零的点,判断这唯一的极值点是极大值点即可;(2)即函数 ( )F x 的导数
在 (0,3] 小于或者等于 1
2
恒成立,分类参数后转化为函数的最值;(3)研究函数是单调性得到函数的极值
点,根据函数图象的变化趋势,判断何时方程 22 ( )mf x x 有唯一实数解,得到 m 所满足的方程,解方程
求解 m 。
【解析】(1)依题意,知 )(xf 的定义域为(0,+∞),
当
2
1 ba 时, xxxxf 2
1
4
1ln)( 2 ,
x
xxxxxf 2
)1)(2(
2
1
2
11)(' (2′)令 )(' xf =0,
解得 1x .(∵ 0x )
因为 0)( xg 有唯一解,所以 0)( 2 xg ,当 10 x 时,
0)(' xf ,此时 )(xf 单调递增;
当 1x 时, 0)(' xf ,此时 )(xf 单调递减。
所以 )(xf 的极大值为
4
3)1( f ,此即为最大值………4 分
(2)
x
axxF ln)( , ]3,0(x ,
则有 2
0
0
0 )('
x
axxFk ≤
2
1 ,在 ]3,0(0 x 上恒成立,
所以 a ≥ max0
2
0 )2
1( xx , ]3,0(0 x (8′)
当 10 x 时, 0
2
02
1 xx 取得最大值
2
1 ,
所以 a ≥
2
1 ………8 分
(3)因为方程 2)(2 xxmf 有唯一实数解,
所以 02ln22 mxxmx 有唯一实数解,
设 mxxmxxg 2ln2)( 2 ,
则
x
mmxxxg 222)('
2 .令 0)(' xg , 02 mmxx .
因为 0m , 0x ,所以 02
42
1 mmmx (舍去),
2
2
4
2
m m mx ,
当 ),0( 2xx 时, 0)(' xg , )(xg 在(0, 2x )上单调递减,
当 ),( 2 xx 时, 0)(' xg , )(xg 在( 2x ,+∞)单调递增
当 2xx 时, )(' 2xg =0, )(xg 取最小值 )( 2xg .(12′)
则
,0)('
,0)(
2
2
xg
xg 既
.0
,02ln2
2
2
2
22
2
2
mmxx
mxxmx
所以 0ln2 22 mmxxm ,因为 0m ,所以 01ln2 22 xx (*)
设函数 1ln2)( xxxh ,因为当 0x 时,
)(xh 是增函数,所以 0)( xh 至多有一解.
因为 0)1( h ,所以方程(*)的解为 2 1x ,即
2 4 12
m m m ,
解得
2
1m .…12 分
【考点】导数及其应用。
【点评】本题考查导数在研究函数性质、研究不等式和方程问题中的综合运用,试题的难度不大,但考查
点极为全面。本题的难点是第三问中方程解的研究,当函数具有极值点时,在这个极值点左右两侧,函数
的单调性是不同的,这样就可以根据极值的大小,结合函数图象的变化趋势确定方程解的个数,如本题中
函数在定义域内有唯一的极值点,而且是极小值点,也就是最小值点,如果这个最小值小于零,函数就出
现两个零点,方程就有两个不同的实数解,只有当这个最小值等于零时,方程才有一个实数解,而最小值
等于零的这个极小值点 x 满足在此点处的导数等于零,函数值也等于零,即我们的【解析】中的方程组
2
2
( ) 0,
'( ) 0
g x
g x
,由这个方程组求解 m 使用了构造函数通过函数的性质得到 2x 的方法也是值得仔细体会的技
巧。
63.(安徽省蚌埠二中 2011 届高三第二次质检文)
(本题满分 12)设函数 axxxxf 2coscossin3)( 。(1)写出函数 )(xf 的最小正周期及单调递
减区间;(2)当
3,6
x 时,函数 )(xf 的最大值与最小值的和为
2
3 ,求 )(xf 的图象、y 轴的正半轴
及 x 轴的正半轴三者围成图形的面积。
答案 (1)最小正周期 T ,单调递减区间是 )(3
2,6 Zkkk
(2)
4
32
2
1)62sin(2
0
xs
64.(安徽省蚌埠二中 2011 届高三第二次质检文)
(本小题满分 13 分)已知函数 1)1()1ln()( xkxxf 。
(1)求函数 )(xf 的单调区间;
(2)若 0)( xf 恒成立,试确定实数 k 的取值范围;
(3)证明:
n
i
nNnnn
i
i
2
)1,(,4
)1())1(
ln(
答案 (1)
1
1
1
1)(
x
kxkkxxf
当 0k 时,有 0)( xf ,此时 ,在 1)(xf 上单调递增,
当 0k 时,此时 )11)( k
kxf ,在( 单调递增,在 ),1(
k
k 上单调递减。
(2) 0)( xf 恒成立
1
1)1ln(
x
xk 在 ),1( 恒成立, 1k ,
(3)证明略。
65.(安徽省合肥八中 2011 届高三第一轮复习四考试理)(3 分)已知函数 2 2( ) ln ( ).f x x a x ax a R
(1)求 ( )f x 的单调区间与极值;
(2)若函数 ( )f x 在区间(1,+ )上是单调减函数,求实数 a 的取值范围。
答案
66.(北京市房山区 2011 年高三上学期期末统练试卷文)(本小题满分 14 分)
已知函数 ( ) lnf x ax x ( )aR .
(Ⅰ)若 2a ,求曲线 ( )y f x 在 1x 处切线的斜率;
(Ⅱ)求 ( )f x 的单调区间;
(Ⅲ)设 2( ) 2 2g x x x ,若对任意 1 (0, )x ,均存在 2 0,1x ,使得 1 2( ) ( )f x g x ,求 a 的取
值范围.
答案 (本小题满分 14 分)
解:(Ⅰ)由已知 1( ) 2 ( 0)f x xx
, ………………2 分
(1) 2 1 3f .
故曲线 ( )y f x 在 1x 处切线的斜率为3 . ………………4 分
(Ⅱ) 1 1'( ) ( 0)axf x a xx x
. ………………5 分
①当 0a 时,由于 0x ,故 1 0ax , '( ) 0f x
所以, ( )f x 的单调递增区间为 (0, ) . ………………6 分
②当 0a 时,由 '( ) 0f x ,得 1x a
.
在区间 1(0, )a
上, ( ) 0f x ,在区间 1( , )a
上 ( ) 0f x ,
所以,函数 ( )f x 的单调递增区间为 1(0, )a
,单调递减区间为 1( , )a
.
………………8 分
(Ⅲ)由已知,转化为 max max( ) ( )f x g x . ………………9 分
max( ) 2g x ………………10 分
由(Ⅱ)知,当 0a 时, ( )f x 在 (0, ) 上单调递增,值域为 R ,故不符合题意.
(或者举出反例:存在 3 3(e ) e 3 2f a ,故不符合题意.) ………………11 分
当 0a 时, ( )f x 在 1(0, )a
上单调递增,在 1( , )a
上单调递减,
故 ( )f x 的极大值即为最大值, 1 1( ) 1 ln( ) 1 ln( )f aa a
, ………13 分
所以 2 1 ln( )a ,
解得 3
1
ea . ………………14 分
题组二
选择题
1.(浙江省杭州市高级中学 2011 届高三理)定义两种运算: 22 baba , 2)( baba ,则函
数 2)2(
2)(
x
xxf 为( )
(A)奇函数 (B)偶函数
(C)奇函数且为偶函数 (D)非奇函数且非偶函数
答案 A.
2.(江西省上高二中 2011 届高三理)若函数 f(x)=x- p
x
+p
2
在(1,+∞)上是增函数,则实数 p 的取值范围
是
A.[-1,+∞) B.[1,+∞) C.(-∞,-1] D.(-∞,1]
答案 A.
3.(福建省四地六校联考 2010-2011 学年高一) 若对于任意实数 x,都有 f(-x)=f(x),且 f(x)在(-∞,0]
上是增函数,则 ( )
A、f(- 3
2 )0 时,方程 f(x)=0 只有一个实根
③f(x)的图象关于(0,c)对称 ④方程 f(x)=0 至多两个实根
其中正确的命题是( )
A.①④ B.①③ C.①②③ D.①②④
答案 C.
20.(四川省成都外国语学校 2011 届高三 10 月理)设函数 f(x) 是定义在 R 上的
以 5 为周期的奇函数,若 f(2)>1,
3
3)2008(
a
af ,则 a 的取 值范围是( )
A. )0,( B.(0,3)
C.(0,+ ∞) D.(-∞,0)∪(3,+ ∞)
答案 B.
21.(四川省成都外国语学校 10-11 学年高一)下列各组函数 )()( xgxf 与 的图象相同的是( )
A. 2)()(,)( xxgxxf
B. 22 )1()(,)( xxgxxf
C. 0)(,1)( xxgxf
D.
x
xxgxxf )(|,|)( )0(
)0(
x
x
答案 D.
22.(四川省成都外国语学校 2011 届高三 10 月理)当 0x 时, 2
2
1 1f x x xx x
最小值为( )
A.1 B. 0 C. 2 D.4
答案 D.
23.(四川省成都外国语学校 2011 届高三 10 月理)定义在 R 上的函数 )(xfy ,在(-∞,a)上是增函
数,且函数 )( axfy 是偶函数,当 axax 21 , ,且 axax 21 时,有 ( )
A. )2()2( 21 xafxaf B. )2()2( 21 xafxaf
C. )2()2( 21 xafxaf D. )2()2( 21 axfxaf
答案 A.
24.(四川省成都外国语学校 2011 届高三 10 月文)设 )(xf 是定义在 R 上的偶函数,对 Rx ,都有
)2()2( xfxf ,且当 ]0,2[x 时, 1)2
1()( xxf ,若在区间 ]6,2( 内关于 x 的方程 0log)( )2( x
axf ( a
>1)恰有 3 个不同的实根,则 a 的取值范围是( )
A.(1,2) B. ),2( C. )4,1( 3 D. )2,4(3
答案 D.
25.(山西省四校 2011 届高三文)幂函数 y=(m2 m 1)xm2-2m-3,当 x∈(0,+∞)时为减函数,则实数 m 的
值是( )
A.m=2 B.m= 1 C.m= 1 或 2 D.m≠1 5
2
答案 A.
26.(四川省成都外国语学校 2011 届高三理)定义在 R 上的函数 )(xfy ,在(-∞,a)上是增函数,且
函数 )( axfy 是偶函数,当 axax 21 , ,且 axax 21 时,有 ( )
A. )2()2( 21 xafxaf B. )2()2( 21 xafxaf
C. )2()2( 21 xafxaf D. )2()2( 21 axfxaf
答案 A.
27.(福建省福州八中 2011 届高三文) 函数
)0(12
)0(2
x
xxy x
的图象大致是
答案 D.
28.(山东省实验中学 2011 届高三文理)某商品销售量 y(件)与销售价格 x(元/件)负相关,则其回归
方程可能是 ( )
A. ^
10 200y x B. ^
10 200y x
C. ^
10 200y x D. ^
10 200y x
答案 A.
29.(广西桂林中学 2011 届高三理)已知 x1 是方程 2010lg xx 的根,x2 是方程 201010 xx 的根,
则 x1·x2=( )
A.2008 B.2009 C.2010 D.2011
答案 C.
30.(福建省四地六校联考 2011 届高三理)将函数 =sin (x+ ) (x R)6y 的图象上所有的点向左平移
4
个单
位长度,再把图象上各点的横坐标扩大到原来的 2 倍,则所得的图象的解析式为 ( )
A. 5=sin (2x+ ) (x R)12y B. x 5=sin ( + ) (x R)2 12y
C. x=sin ( - ) (x R)2 12y D. x 5=sin ( + ) (x R)2 24y
答案 B.
31 . ( 吉 林 省 实 验 中 学 2011 届 高 三 文 ) 设 a > 1 , 函 数 f ( x ) =a|x| 的 图 像 大 致 是
( )
答案 A.
32.(河 南信阳市 2011 届高 三理)已 知函数 ① 2
3( ) 5f x x
② cos( ) 5 xf x e ; ③ ( ) 5 xf x e ;④
( ) 5lnf x x 。 其 中 对 于 ( )f x 定 义 域 内 的 任 意 一 个 自 变 量 1x , 都 存 在 唯 一 的 自 变 量 2x , 使
1 2( ) ( ) 5f x f x 成立的函数为 ( )
A.①③④ B.②④ C.①③ D.③
答案 D.
33.(四川省成都市 2011 届高三理)已知定义域为 R 的函数 ( )f x 在 ),8( 上为减函数,且 ( 8)y f x
函数为偶函数,则
A. (6) (7)f f B. (6) (9)f f
C. (7) (9)f f D. (7) (10)f f
答案 D.
34.(浙江省杭州市 2011 届高三文)右图是函数 baxxxf 2)( 的部分图象,则函数 ( ) ln ( )g x x f x
的零点所在的区间是 ( )
A 1 1( , )4 2 B (1,2)
1( ,1)2 D (2,3)
答案 B
35.(四川省成都外国语学校 2011 届高三 10 月理)已知函数 y=log2x 的反函数是 )(1 xfy ,则函数
)1(1 xfy 的图象是( )
答案 C.
36.(广东省广州东莞五校 2011 届高三理)函数 cosy x 的一个单调递增区间为
A. ,2 2
B. 0, C. 3,2 2
D. ,2
答案 D.
37.(山西省四校 2011 届高三文)函数 y=log2(x+4)-3x 零点的个数为( )
A.0 B.1 C.2 D.3
答案 C.
38.(浙江省吴兴高级中学 2011 届高三文)
已知函数 2( ) ( 3 2)ln 2008 2009f x x x x x ,则函数 ( )f x 在下面哪个范围
内必有零点 ( )
A、 (0,1) B、 (1,2) C、 (2,3) D、 (2,4)
答案 B
39.(河北省唐山一中 2011 届高三文)若函数 f(x)=ax3+bx2+cx+d 有极值,则导函数 f’(x)的图象不可能
是 ( )
x
y
O
f'(x)
x0 x
y
O
f'(x)
x1 x2 x
y
O
f'(x)
x1 x2 x
y
O
f'(x)
x0
A B C D
答案 A.
40. (广西桂林中学 2011 届高三理) 已知函数 )(xf 的反函数 )(1 xf 图像经过点 )0,1(A ,则函数
)1( xfy 的图像必经过点( )
A. )1,1( B. )1,0( C. )2,1( D. )1,1(
答案 A.
41.(河南信阳市 2011 届高三理)已知二次函数 ( )f x 的图象如右图所示,则其导函数 ( )f x 的图象大致形
状是 ( )
答案 B.
填空题
42. (浙江省杭州市高级中学 2011 届高三文)若 21 3f x a x ax 是偶函数,则 f x 的递增区
间为______________
答案 (0,1]
43.(江苏泰兴重点中学 2011 届高三文)已知函数 ( )y f x 是奇函数,当 0x 时, 2( ) ( R)f x x ax a ,
(2) 6f ,则 a _________
答案 5.
44.(江苏泰兴重点中学 2011 届高三理)设函数 ( )f x 是定义在 R 上以 3 为周期的奇函数,若 (1) 1f ,
2 3(2) 1
af a
,则 a 的取值范围是__________________________.
答案 21 3a
45.(湖南岳阳县一中 2011 届高三理)已知函数 ( )f x 是定义域为 R 的偶函数,且 1( 1) ( )f x f x
,若 ( )f x
在[ 1,0] 上是减函数,那么 ( )f x 在[2,3]上是 ( )
A. 增函数 B. 减函数 C. 先增后减的函数 D. 先减后增的函数
答案 A.
46.(江苏泰兴重点中学 2011 届高三文)函数 xxxf sin2 在 ,0 上的单调增区间为
答案 { , }3
47.(广东省湛江一中 2011 届高三理)若函数
0,
0,
0,2
)(
xbx
xa
xx
xf 是奇函数,则 _______ ba
答案: 2 2,0 ba
48.(江苏泰兴市重点中学 2011 届理)已知 2( ) lg( 8 7)f x x x 在 ( , 1)m m 上是增函数,则 m 的取值
范围是 .
答案 1 3m 。
49.(广东省湛江一中 2011 届高三 10 月月考理)
若函数
0,
0,
0,2
)(
xbx
xa
xx
xf 是奇函数,则 _______ ba .
答案: 2,0 ba
50.(广西桂林中学 2011 届高三 11 月月考试题文)
已知函数 )(xf 是 ),( 上的偶函数,若对于 0x ,都有 )()2( xfxf ,且当 2,0x 时,
2( ) log ( 1)f x x , ( 2011) (2010)f f 的值为 .
答案 -1.
51.(2011 湖南嘉禾一中)函数 )1()( xxxf 的反函数是 .
答案. )1(2 xxy
52.(江苏泰兴 2011 届高三理)函数
2
2 ( )1
xy x Rx
的值域为________________.
答案 0,1
53.(江苏泰兴2011届高三理)设函数 ( )f x 是定义在R上以3为周期的奇函数,若 (1) 1f , 2 3(2) 1
af a
,
则 a 的取值范围是__________________________.
答案 21 3a
54.(江省吴兴高级中学 2011 届高三文)下列五个函数中:① xy 2 ; ② xy 2log ; ③ 2xy ; ④ 1 xy ;
⑤ xy 2cos ,
当 10 21 xx 时,使
2
)()()2( 2121 xfxfxxf 恒成立的函数是 (将正确的序号都填上).
答案 ②
55.(江苏泰兴市重点中学 2011 届理)函数 f(x)=-x2+4x-1 在[t,t+1]上的最大值为 g(t),则 g(t)的最
大值为____________.
答案 3.
56.(江苏泰兴 2011 届高三理)函数 f(x)=-x2+4x-1 在[t,t+1]上的最大值为 g(t),则 g(t)的最大值为
____________.
答案 3.
57.(江苏泰兴 2011 届高三文)
设函数 1( )f x x x
,对任意的 1,x , ( ) ( ) 0f mx mf x 恒成立,则实数 m 的取值范围是
____________.
答案 1m
58.(江西省上高二中 2011 届高三理)
已知函数 f(x)= ,2))((
.0,cos2
,0,)( 0
2
xff
xx
xxxf 若
则 x0= .
答案 3π
4
59.(四川省成都外国语学校 10-11 学年高一)已知函数 )(xf 是定义在实数集 R 上的不恒为零的偶函数,且
对任意实数 x 都有 )()1()1( xfxxxf ,则 )2
5(f 的值是 答案 0.
60.(江苏泰兴市重点中学 2011 届高三理)
已知 2( ) lg( 8 7)f x x x 在 ( , 1)m m 上是增函数,则 m 的取值范围是 .
答案 1 3m
61.(江西省上高二中 2011 届高三理)若对于任意 a∈[-1,1],函数 f(x)=x2+(a-4)x+4-2a 的值恒大
于零,则 x 的取值范围是 .
答案 (-∞‚1)∪(3,+∞);
三. 解答题
62.(江西省上高二中 2011 届高三理)函数
x
axxf 2)( 的定义域为(0,1]( a 为实数).
⑴当 1a 时,求函数 )( xfy 的值域;
⑵若函数 )( xfy 在定义域上是减函数,求 a 的取值范围;
⑶求函数 )( xfy 在 x∈(0,1]上的最大值及最小值,并求出函数取最值时 x 的值.
答案 解:(1)显然函数 )( xfy 的值域为 ),22[ ;
(2)若函数 )( xfy 在定义域上是减函数,则任取 21, xx ]1.0( 且 21 xx 都有 )()( 21 xfxf 成
立, 即 0)2)((
2121 xx
axx
只要 212 xxa 即可,由 21, xx ]1.0( ,故 )0,2(2 21 xx ,所以 2a ,
故 a 的取值范围是 ]2,( ;
(3)当 0a 时,函数 )( xfy 在 ]1.0( 上单调增,无最小值,当 1x 时取得最大值 a2 ;
由(2)得当 2a 时,函数 )( xfy 在 ]1.0( 上单调减,无最大值,
当 x=1 时取得最小值 2-a;
当 02 a 时,函数 )( xfy 在 ].0( 2
2a 上单调减,在 ]1,[ 2
2a 上单调增,无最大值,
当 2
2ax 时取得最小值 a22 .
63.(广东省广州东莞五校 2011 届高三理) (本小题满分 14 分)
已知函数 )0(2)1ln()( 2 kxkxxxf 。
(1)当 2k 时,求曲线 )(xfy 在点 ))1(,1( f 处的切线方程;
(2)求 )(xf 的单调区间。
答案 (本小题满分 14 分)
解:(1)当 2k 时, 2)1ln()( xxxxf , xxxf 211
1)(/
由于
2
3)1(,2ln)1( / ff ,
所以曲线 )(xfy 在点 ))1(,1( f 处的切线方程为 )1(2
32ln xy
即 032ln223 yx 。 ………4 分
(2) ),1(,1
)1()(/
xx
kkxxxf .………5 分
①当 0k 时,
x
xxf
1)(/ .
所以,在区间 )0,1( 上, 0)(/ xf ;在区间 ),0( 上, 0)(/ xf .
故 )(xf 的单调递增区间是 )0,1( ,单调递减区间是 ),0( .………6 分
②当 10 k 时,由 01
)1()(/
x
kkxxxf ,得 01 x , 01
2
k
kx
所以,在区间 )0,1( 和 ),1(
k
k 上, 0)(/ xf ;在区间 )1,0( k
k 上, 0)(/ xf
故 )(xf 的单调递增区间是 )0,1( 和 ),1(
k
k ,单调递减区间是 )1,0( k
k
.………9 分
③当 1k 时,
x
xxf
1)(
2
/ ,故 )(xf 的单调递增区间是 ),1( .………10 分
④当 1k 时, 01
)1()(/
x
kkxxxf ,得 0),0,1(1
21 xk
kx .
所以没在区间 )1,1( k
k 和 ),0( 上, 0)(/ xf ;在区间 )0,1( k
k 上, 0)(/ xf
故 ( )f x 的单调递增区间是 )1,1( k
k 和 ),0( ,单调递减区间是 )0,1( k
k ………13 分
由上可知当 0k 时, )(xf 的单调递增区间是 )0,1( ,单调递减区间是 ),0( ;当 10 k 时, )(xf 的
单调递增区间是 )0,1( 和 ),1(
k
k ,单调递减区间是 )1,0( k
k ;当 1k 时, )(xf 的单调递增区间是
),1( ;当 1k 时, ( )f x 的单调递增区间是 )1,1( k
k 和 ),0( ,单调递减区间是 )0,1( k
k ………
14 分
64. ( 广 东 省 广 州 东 莞 五 校 2011 届 高 三 文 )( 本 小 题 满 分 14 分 ) 已 知 函 数
1( ) ln , (0, )f x x ax xx
( a 为实常数).
(1)当 0a 时,求 ( )f x 的最小值;
(2)若 ( )f x 在[2, ) 上是单调函数,求 a 的取值范围.
答案 (本题满分 14 分)
(1) 0a 时, 2
1( ) xf x x
,
当 0 1x 时, ( ) 0f x ,
当 1x 时, ( ) 0f x ,
∴ min( ) (1) 1.f x f ……6 分
(2) 2
1 1( )f x ax x
2
2
1.ax x
x
当 0a 时, 2 1ax x 在[2, ) 上恒大于零,即 ( ) 0f x ,符合要求. ……9 分
当 0a 时,令 2( ) 1g x ax x ,
( )g x 在[2, ) 上只能恒小于或等于零.
故 1 4 0a 或
1 4 0
(2) 0
1 22
a
g
a
,
解得 1 .4a ……13 分
∴ a 的取值范围是 1( , ] [0, ).4
……14 分
65.(河南许昌市四校 2011 届高三)(本小题满分 12 分)函数 f(x)对任意的实数 m,n,有 f(m+n)=f
(m)+f(n),当 x>0 时,有 f(x)>0。
①求证: 0)0( f
②求证:f(x)在(-∞,+∞)上为增函数.
③若 f(1)=1,解不等式 f(4x-2x)<2.
答案 28.证明:① 令 0 nm ,则 (0 0) (0) (0) 2 (0)f f f f
0)0( f (3 分)
②令 mn ,则 )()()( mfmfmmf
)()()0( mfmff
)()( mfmf
)(xfy 是奇函数。
在(-∞,+∞)上任取 212,1 x xxx 且 则 012 xx
0)()()()()( 121212 xfxfxfxfxxf
即 )()( 21 xfxf
函数 )(xfy 是增函数 (8 分)
③原不等式可化为 )2()1()1(11)24( ffff xx
由②得: 224 xx , 022)2( 2 xx
221 x 又 02 x
1x
故,原不等式的解集为{x|x<1}. (12 分)
66.(江苏省 2011 届高三理)已知函数 )2lg()(
x
axxf ,其中 a 是大于 0 的常数
(1) 求函数 )(xf 的定义域;
(2) 当 )4,1(a 时,求函数 )(xf 在[2, ) 上的最小值;
(3) 若对任意 ),2[ x 恒有 0)( xf ,试确定 a 的取值范围
答案 (本题满分 14 分)
解(1) 由 02
x
ax 得, 022
x
axx
解得 1a 时,定义域为 ),0( ………………………………2 分
1a 时,定义域为 0|{ xx 且 }1x …………………1 分
10 a 时,定义域为 axx 110|{ 或 ax 11 }……2 分
(2) 设 2)(
x
axxg ,当 )4,1(a , ),2[ x 时
则 01)( 2
2
2
x
ax
x
axg 恒成立,∴ 2)(
x
axxg 在 ),2[ 上是增函数
∴ )2lg()(
x
axxf 在 ),2[ 上是增函数…………………………3 分
∴ )2lg()(
x
axxf 在 ),2[ 上的最小值为
2lg)2( af ……………2 分
(3) 对任意 ),2[ x 恒有 0)( xf ,
即 12
x
ax 对 ),2[ x 恒成立
∴ 23 xxa ,而
4
9)2
3(3)( 22 xxxxh 在 ),2[ x 上是减函数
∴ 2)2()( max hxh ,∴ 2a ……………………………………5 分
67.(福建省四地六校联考 2011 届高三理)(本小题满分 13 分)已知定义域为 R 的函数
14
1)(
xaxf 是
奇函数.
(I)求 a 的值,并指出函数 )(xf 的单调性(不必说明单调性理由);
(II)若对任意的 Rt ,不等式 0)2()2( 22 ktfttf 恒成立,求 k 的取值范围.
答案 解:(I)函数 )(xf 的定义域为 R,因为 )(xf 是奇函数,所以 0)()( xfxf ,
即 012
41
4
14
12
14
1
14
1
aaaa x
x
xxx
,故
2
1a ……4 分
(另解:由 )(xf 是 R 上的奇函数,所以 0)0( f ,故
2
1a .
再由
)41(2
41
41
1
2
1)( x
x
xxf
,
通过验证 0)()( xfxf 来确定
2
1a 的合理性) ……………4 分
由 ,
14
1
2
1)(
xxf 知 )(xf 在 R 上为减函数 ……………6 分
(II)解法一:由(I)得 )(xf 在 R 上为减函数,
又因 )(xf 是奇函数,从而不等式 0)2()2( 22 ktfttf 等价于
).2()2()2( 222 ktfktfttf ……………9 分
)(xf 在 R 上为减函数,由上式得: .22 22 kttt
即对一切 ,023 2 kttRt 有
从而
3
1,0124 kk 解得 ……………13 分
解法二:由(1)知 ,
242
14)(
x
x
xf 又由题设条件得: 0
242
14
242
14
2
2
2
2
2
2
2
2
kt
kt
tt
tt
即 0)14)(14()14)(14( 2222 2222 ktttttkt ……………9 分
整理得 14 23 2
ktt ,因底数 4>1,故 023 2 ktt
上式对一切 Rt 均成立,从而判别式 .3
1,0124 kk 解得 …………13 分
68.(江苏泰兴 2011 届理)(本小题满分 14 分):已知函数
bx
axxf
21)( 0a 是奇函数,并且函数 )(xf
的图像经过点(1,3),(1)求实数 ba, 的值;(2)求函数 )(xf 的值域
答案 解:(1)函数
bx
axxf
21)( 是奇函数,则 )()( xfxf
0,,0,11 22
bbxbxabx
ax
bx
xa ………(3 分)
又函数 )(xf 的图像经过点(1,3), ,0,31
1,3)1(
bb
af
∴a=2 ……(6 分)
(2)由(1)知 01221)(
2
xxxx
xxf ………(7 分)
当 0x 时, ,2212212
xxxx 当且仅当 ,12 xx
即
2
2x 时取等号…(10 分)
当 0x 时, 2212,2212212
xxxxxx
当且仅当 ,1)2( xx 即
2
2x 时取等号……………(13 分)
综上可知函数 )(xf 的值域为 ,2222, …………(12 分)
69.(江苏泰兴 2011 届高三理)(本题满分 16 分)设二次函数 2( )f x ax bx c 在区间 2,2 上的最大
值、最小值分别是 M、m,集合 | ( )A x f x x .
(1)若 {1,2}A ,且 (0) 2f ,求 M 和 m 的值;
(2)若 {1}A ,且 1a ,记 ( )g a M m ,求 ( )g a 的最小值.
答案 (1)由 (0) 2 2f c 可知 ,……………………………1 分
又 2A 1 2 1 2 ( 1) 0 .ax b x c , ,故 ,是方程 的两实根
1-b1+2= a ,c2= a
…………………3 分 1, 2a b 解得 …………4 分
2 2( ) 2 2 ( 1) 1, 2,2f x x x x x
min1 ( ) (1) 1, 1x f x f m 当 时, 即 ……………………………5 分
max2 ( ) ( 2) 10, 10.x f x f M 当 时, 即 ……………………………6 分
(2) 2 ( 1) 0ax b x c 由题意知,方程 有两相等实根x=2,x=1
∴
a
c
a
b
2
111
, 即
ac
ab 21 ……………………………8 分
∴f(x)=ax2+(1-2a)x+a, x∈[-2,2] 其对称轴方程为 x=
a
a
2
14 1 a2
1
又 a≥1,故 1-
1,2
1
2
1
a
……………………………9 分
∴M=f(-2)=9a-2 …………………………10 分
m=
aa
af 4
11)2
12( ……………………………11 分
g(a)=M+m=9a-
a4
1 -1 ……………………………14 分
min
63( ) 1, 1 ( ) .4g a a g a 又 在区间 上为单调递增的, 当 时, = 4
31 ………16 分
70.(四川省成都外国语学校 10-11 学年高一)(本小题 12 分)已知奇函数
2
2
2 ( 0)
( ) 0 ( 0)
( 0)
x x x
f x x
x mx x
(1)求实数 m 的值,并在给出的直角坐标系中画出 ( )y f x 的图象;
(2)若函数 f(x)在区间[-1,|a|-2]上单调递增,试确定 a 的取值范围.
答案 (1)当 x<0 时,-x>0, 2 2( ) ( ) 2( ) 2f x x x x x
又 f(x)为奇函数,∴ 2( ) ( ) 2f x f x x x ,
∴ f(x)=x2+2x,∴m=2
y=f(x)的图象如右所示
(2)由(1)知 f(x)=
2
2
2 ( 0)
0 ( 0)
2 ( 0)
x x x
x
x x x
,
由图象可知, ( )f x 在[-1,1]上单调递增,要使 ( )f x 在[-1,|a|-2]上单调递增,只需 | | 2 1
| | 2 1
a
a
解之得 3 1 1 3a a 或
71.(四川省成都外国语学校 10-11 学年高一)(本小题 12 分)已知定义在 R 上的函数 ( )f x 对任意实数 x 、
y 恒有 ( ) ( ) ( )f x f y f x y ,且当 0x 时, ( ) 0f x ,又 2(1) 3f 。
(1)求证 ( )f x 为奇函数;(2)求证: ( )f x 为 R 上的减函数;
(3)解关于 x 的不等式: 1 1(2 ) ( ) ( ) ( )2 2f bx f x f bx f b . ( 2)b 其中
答案 (1),(2)略 (3) 2
2
bx b
。
72.(四川省成都外国语学校 10-11 学年高一)(本小题 14 分)已知函数
xxf 11)( ,(x>0).
(I) 0 , ( ) ( )a b f a f b 当 且 时 ,求 1 1
a b
的值;
(II)是否存在实数 a,b(a0,∴
11 , x 1,x(x) 1 1, 0 x 1.x
f
∴f(x)在(0,1)上为减函数,在 (1, ) 上是增函数.
由 00
而
11 , x 1,x( ) 1 1, 0 x 1.x
f x
①当 )1,0(b,a 时, 1x
1)x(f 在(0,1)上为减函数.
故
.a)b(f
,b)a(f 即
a.1b
1
,b1a
1
解得 a=b.
故此时不存在适合条件的实数 a,b.
② 当 ),1[b,a 时, 1f (x) 1 x
在 (1, ) 上是增函数.
故
.b)b(f
,a)a(f 即
b.b
11
,aa
11
此时 a,b 是方程 01xx 2 的根,此方程无实根.故此时不存在适合条件的实数 a,b.
③ 当 )1,0(a , ),1[b 时,由于 ]b,a[1 ,而 ]b,a[0)1(f ,故此时不存在适合条件的实数 a,b.
综上可知,不存在适合条件的实数 a,b.
73.(山西省四校 2011 届高三文)(满分 12 分)已知函数 f(x)=ax3-bx2+9x+2,若 f(x)在 x=1 处的切线方程为
3x+y-6=0
(Ⅰ)求函数 f(x)的解析式
(Ⅱ)若对任意的 x ]2,4
1[ 都有 f(x) 122 tt 成立,求函数 g(t) 22 tt 的最值
答案 (12 分)
简答:① 923)( 2' bxaxxf ,
3)1(
3)1('
f
f
………2 分
4
12
a
b ………4 分
②列表如下:
x 1
4
1 1,4 2
1
2
1 3,2 2
3
2
3 ,22
2
' ( )f x + 0 -
0 +
( )f x 57
16
11
2
极大值 极小值2 4
f(x) min =2………8 分
对任意的 x ]2,4
1[ 都有 f(x) 122 tt 成立,
f(x) min =2 122 tt , 31 t ………10 分
g(t) 22 tt ( 31 t ),
t=-
2
1 ,最小值-
4
9 ,t=3 最大值 10………………………12 分
74.(山西省四校 2011 届高三文)(满分 12 分)设函数 2( ) 4ln 1f x x x .
(Ⅰ)求函数 )(xf 的单调递增区间;
(Ⅱ)若关于 x 的方程 2 4 0f x x x a 在区间 1,e 内恰有两个相异的实根,求实数 a 的取值范围.
答案 (12 分) 解:(1)函数 f x 的定义域为 0, ,………1 分
∵
24 2( 2) 2( 2)( 1)( ) 2( 1) x x x xf x xx x x
,…………3 分
令 ( ) 0f x 得 0 2x ,故函数 f x 的单调递增区间为 0,2 . ………4 分
(2)方法 1:∵ 2( ) 4ln 1f x x x ,
∴ 2( ) 4 0 4ln 2 1 0 1f x x x a x x a 即 在 ,e 内恰有两个相异的实根。
令 4ln 2 1g x x x a , 4 4 2( ) 2 xg x x x
则 ,………6 分
4 2( ) 0 2xg x xx
令 得
列表如下:
x 1 1,2 2 2,e e
( )g x + 0 -
( )g x (1)g (2)g极大值 ( )g e
(1) 3g a , ( ) 3 2g e e a , 2 4ln 2 5g a
( ) (1)g e g ………8 分
要使 2( ) 4 0 1f x x x a 在 ,e 内恰有两个相异的实根。
只需 ( ) 0 (2)g e g ,即3 2 0 4ln 2 5e a a
3 2 4ln 2 5e a
a 的取值范围是 3 2 ,4ln 2 5e .………12 分
方法 2:∵ 2( ) 4ln 1f x x x ,
∴ 2( ) 4 0 4ln 2 1 1f x x x a x x a 即 在 ,e 内恰有两个相异的实根。
令 4ln 2 1h x x x , 4 4 2( ) 2 xx x x
则h ,………6 分
4 2( ) 0 2xh x xx
令 得
列表如下:
x 1 1,2 2 2,e e
( )h x + 0 -
( )h x (1)h (2)h极大值 ( )h e
(1) 3h , ( ) 3 2h e e , 2 4ln 2 5h
( ) (1)h e h ………8 分
要使 2( ) 4 1f x x x a 在 ,e 内恰有两个相异的实根。
只需 ( ) (2)h e a h ,即3 2 4ln 2 5e a
的取值范围是 3 2 ,4ln 2 5e .……………12。
75.(福建省福州八中 2011 届高三理)(本小题 13 分)
在长为 100 千米的铁路线 AB 旁的 C 处有一个工厂,工厂与铁路的距离 CA 为 20 千米.由铁路上的 B 处向
工厂提供原料,公路与铁路每吨千米的货物运价比为 5∶3,为节约运费,在铁路的 D 处修一货物转运站,
设 AD 距离为 x 千米,沿 CD 直线修一条公路(如图).
(1)将每吨货物运费 y(元)表示成 x 的函数.
(2)当 x 为何值时运费最省?
答案 (本小题 13 分)解:(1)设公路与铁路每吨千米的货物运价 分 别
为 5k、3k(元)(k 为常数)AD=x,则 DB=100-x.
40020 22222 xxACADCD ……………………3 分
∴每吨货物运费 y=(100-x)·3k+ 4002 x ·5k(元)(00,∴解得 x=15……………………………………9 分
当 015 时,y′>0
∴当 x=15 时,y 有最小值.………………………………12 分
答:当 x 为 15 千米时运费最省 .…………………………13 分
76.(河北省唐山一中 2011 届高三文)(本题满分 12 分)
已知函数 f(x)=
3
1 x3-(a+2)x2+a(a+4)x+5 在区间(-1,2)内单调递减,求 a 的取值范围.
答案 解 1:f’(x)=x2-2(a+2)x+a(a+4)=(x-a)(x-a-4),……………………………4 分
f’(x)<0 的解为(a,a+4), ……………………………7 分
∵f(x)在区间(-1,2)内单调递减,
∴(-1,2) (a,a+4),……………………………………………………10 分
由此得 a≤-1 且 a+4≥2,a 的范围是[-2,-1]. ………………12 分
解 2:f’(x)=x2-2(a+2)x+a(a+4), …………………2 分
∵f(x)在区间(-1,2)内单调递减,
∴f’(x)≤0 在区间(-1,2)上恒成立, …………………4 分
∵二次函数 f’(x)=x2-2(a+2)x+a(a+4)的开口向上,
∴f’(-1)=a2+6a+5≤0 且 f’(2)=a2-4≤0 …………………………………10 分
解得 a 的范围是[-2,-1]. ………………………………………………12 分
77.(四川省成都外国语学校 2011 届高三理)(12 分)定义在 R 上的函数 f(x)和 g(x)满足函数
xaxxf ln)( 2 在[1,2]上为增函数, xaxxg )( 在(0,1)为减函数,
(1)求 f(x)和 g(x)的解析式;
(2)当 b>-1 时,若 2
12)( xbxxf 在 ]1,0(x 内恒成立,求 b 的取值范围。
答案 解:
x
ax
x
axxf
222)(
f(x)在[1,2]为增函数, 0)( xf 对 ]2,1[x 恒成立
22xa , 2a
恒成立对 ]1,0[x0
2
1)(
x
axg , 2a
a=2
xxxf ln2)( 2 , xxxg 2)(
(2) 2
12)( xbxxf 在 ]1,0(x 内恒成立
3
1ln22 xx
xxb
令 3
1ln2)( xx
xxxh ,则 24
ln2231)( x
x
xxh
]1,0(x 时, 0)( xh ,故 )(xh 在 ]1,0(x 为减函数
2)1()(2 min hxhb
11 b
78.(江苏泰兴 2011 届高三理)(本题满分 16 分)
已知函数 2 2( ) 2 4 2 f x ax b b x , 2( ) 1 ( ) ( , )g x x a a b R .
(1)当 0b 时,若 ( ) ( , 2]f x 在 上单调递减,求 a 的取值范围;
(2)求满足下列条件的所有整数对 ( , )a b :存在 0x ,使得 0( ) ( )f x f x是 的最大值, 0( ) ( )g x g x是 的最小
值;
(3)对满足(II)中的条件的整数对 ( , )a b ,试构造一个定义在 { |D x x R 且 2 , }x k k Z 上的函
数 ( )h x :使 ( 2) ( )h x h x ,且当 ( 2, 0)x 时, ( ) ( )h x f x .
答案 (1)当 0b 时, 2 4f x ax x ,…………………………………………………1 分
若 0a , 4f x x ,则 f x 在 , 2 上单调递减,符合题意;………3 分
若 0a ,要使 f x 在 , 2 上单调递减,
必须满足
0,
4 2,2
a
a
……………………………………………………………………5 分
∴ 0 1a .综上所述,a 的取值范围是 0, 1 …………………………………6 分
(2)若 0a , 22 4 2f x b b x ,则 f x 无最大值,………………………7 分
故 0a ,∴ f x 为二次函数,
要使 f x 有最大值,必须满足 2
0,
4 2 0,
a
b b
即 0a 且1 5 1 5b ,…8 分
此时, 2
0
4 2b bx a
时, f x 有最大值.………………………………………分
又 g x 取最小值时, 0x a ,………………………………………………………分
依题意,有 24 2b b aa
Z ,则 22 24 2 5 1a b b b ,…………分
∵ 0a 且1 5 1 5b ,∴ 20 5a a Z ,得 1a ,………………分
此时 1b 或 3b .
∴满足条件的整数对 ,a b 是 1, 1 , 1, 3 .……………………………12 分
(3)当整数对是 1, 1 , 1, 3 时, 2 2f x x x
( 2) ( )h x h x , ( )h x 是以 2 为周期的周期函数,………………………分
又当 2, 0x 时,,构造 ( )h x 如下:当 2 2, 2 ,x k k k Z ,则,
22 2 2 2 2h x h x k f x k x k x k ,
79.(江西省上高二中 2011 届高三理)函数
x
axxf 2)( 的定义域为(0,1]( a 为实数).
⑴当 1a 时,求函数 )( xfy 的值域;
⑵若函数 )( xfy 在定义域上是减函数,求 a 的取值范围;
⑶求函数 )( xfy 在 x∈(0,1]上的最大值及最小值,并求出函数取最值时 x 的值.
故 22 2 2 , 2 2, 2 , .h x x k x k x k k k Z …
答案 解:(1)显然函数 )( xfy 的值域为 ),22[ ;
(2)若函数 )( xfy 在定义域上是减函数,则任取 21, xx ]1.0( 且 21 xx 都有 )()( 21 xfxf 成
立, 即 0)2)((
2121 xx
axx
只要 212 xxa 即可,由 21, xx ]1.0( ,故 )0,2(2 21 xx ,所以 2a ,
故 a 的取值范围是 ]2,( ;
(3)当 0a 时,函数 )( xfy 在 ]1.0( 上单调增,无最小值,当 1x 时取得最大值 a2 ;
由(2)得当 2a 时,函数 )( xfy 在 ]1.0( 上单调减,无最大值,
当 x=1 时取得最小值 2-a;
当 02 a 时,函数 )( xfy 在 ].0( 2
2a 上单调减,在 ]1,[ 2
2a 上单调增,无最大值,
当 2
2ax 时取得最小值 a22 .
80.(四川省成都外国语学校 2011 届高三 10 月文)
(12 分)已知函数 xxxxxxf cossinsin3)3sin(cos2)( 2 。
(1)求函数 )(xf 的最小正周期及单调增区间;
(2)若当 ]12
7,12[ x 时, )(xf 的反函数为 )(1 xf ,求 )1(1f 的值。
答案 解:(1) )32sin(2)( xxf T=
223222 kxk , Zk
增区间 ]12,12
5,[ kk , Zk
(2)令 1)32sin(2 x 又 ]12
7,12[ x ∴
6
5
32 x ∴
4
x
81.(河南信阳市 2011 届高三理)本小题满分 12 分)
设 M 是由满足下列条件的函数 ( )f x 构成的集合:“①方程 ( ) 0f x x 有实数根;②函数
( ) ( ) 0 ( ) 1.f x f x f x 的导数 满足 ”
(I)判断函数 sin( ) 2 4
x xf x 是否是集合 M 中的元素,并说明理由;
( II ) 集 合 M 中 的 元 素 ( )f x 具 有 下 面 的 性 质 : 若 ( )f x 的 定 义 域 为 D , 则 对 于 任 意
0 0[ , ] , [ , ], ( ) ( ) ( ) ( )m n D x m n f n f m n m f x 都存在 使得等式 成立。试用这一性质证明:方程
( ) 0f x x 只有一个实数根;
(III)对于 M 中的函数 1( ), ( ) 0f x x f x x 设 是方程 的实数根,求证:对于 ( )f x 定义域中任意的
2 3, ,x x 当 2 1| | 1,x x 且 3 1 3 2| | 1 ,| ( ) ( ) | 2.x x f x f x 时
答案 (1)因为 1 1'( ) cos ,2 4f x x
所以 1 3'( ) [ , ] 0 '( ) 1.4 4f x f x 满足条件
又因为当 0 , (0) 0x f 时 ,所以方程 ( ) 0f x x 有实数根 0,
所以函数 sin( ) 2 4
x xf x 是集合 M 中的元素。 …………4 分
(2)假设方程 ( ) 0f x x 存在两个实数根 , ( ) ,
则 ( ) 0, ( ) 0,f f …………5 分
不妨设 ,根据题意存在数 ( , )c ,
使得等式 ( ) ( ) ( ) '( )f f f c 成立, …………7 分
因为 ( ) , ( ) , , '( ) 1f f f c 且 所以
与已知 0 '( ) 1 , ( ) 0f x f x x 矛盾 所以方程 只有一个实数根;
…………9 分
(3)不妨设 2 3 , '( ) 0,x x f x 因为 所以f(x)为增函数,
所以 2 3( ) ( ),f x f x
又因为 '( ) 1 0,f x 所以函数f(x)-x 为减函数, …………10 分
所以 2 2 3 3( ) ( ) ,f x x f x x …………11 分
所以 3 2 3 20 ( ) ( )f x f x x x ,
即 3 2 3 2| ( ) ( ) | | |f x f x x x
所以 3 2 3 2 3 1 2 1 3 1 2 1| ( ) ( ) | | | | ( ) | | | | | 2.f x f x x x x x x x x x x x
…………12 分
题组三
一、选择题
1.(四川省成都市 2010 届高三第三次诊断理科)设 f(x)是定义在 R 上的偶函数,对 x∈R,都有 f(x-2)=
f(x+2),且当 x∈[-2,0]时,f(x)=( 1
2 )x-1,若在区间(-2,6]内关于 x 的方程 f(x)-loga(x+2)=0(a>1)
恰有 3 个不同的实数根,则 a 的取值范围是( )
(A)(1,2) (B)(2,+∞) (C)(1, 3 4 ) (D)( 3 4 ,2)
答案 D
【解析】由 f(x-2)=f(x+2),知 f(x)是周期为 4 的周期函数
于是可得 f(x)在(-2,6]上的草图如图中实线所示
而函数 g(x)=loga(x+2)(a>1)的图象如图中虚线所示
结合图象可知,要使得方程 f(x)-loga(x+2)=0(a>1)
在区间(-2,6]内恰有 3 个不同的实数根,
必需且只需 (2) 3
(6) 3
g
g
,所以 g 4 3
8 3
a
a
lo
log
,解得: 3 4 <a<2。
2.(四川省自贡市 2010 届高三三诊理科试题)函数 2 2 ( 4)xy x 的定义域为( )
A.{ | 0}x x B.{ | 0x x 且 4}x
C.{ | 1}x x D.{ | 1x x 且 4}x
答案 D
3.(广东省江门市 2010 届高三数学理科 3 月质量检测试题)函数
xxay x
(0 1)a 的图象的大致形状是
( D )
答案 D
【解析】因为 , 0
, 0
xx
x
a xxay x a x
, 0 1a ,所以选 D.
【考点定位】本题考查函数的图象,函数是高中数学的主干知识,是高考的重点和热点,在高考中占整个试卷
的 1
3
左右.
【备考要点】复习时,要立足课本,务实基础(特别是函数的图象与性质等)。
-2 0 2 4 6 x
y
3 y=loga(x+2)
4.(四川省雅安市 2010 届高三第三次诊断性考试理科)已知函数 ( )f x 的定义域为
[ 3, ) ,部分函数值如表所示,其导函数的图象如图所示,若正数 a ,b 满足 (2 ) 1f a b ,则 2
2
b
a
的取值范围是( )
A. 2( ,1)5 B. 2( ,4)5 C. (1,4) D. 2( , ) (4, )5
答案 B
5.(四川省南充高中 2010 届高三 4 月月考文科试题)
已知函数 1)6()( 23 xaaxxxf 有极大值和极小值,则实数 a 的取值范围是( )
A.-1<a<2 B.-3<a<6
C.a<-1 或 a>2 D.a<-3 或 a>6
答案 D
6 . ( 四 川 省 成 都 市 石 室 中 学 2010 届 高 三 三 诊 模 拟 理 科 ) 若 a 、 b 为 实 数 , 集 合
xxfaNa
bM :},0,{},1,{ 表示把集合 M 中的元素 x 映射到集合 N 中仍为 x,则 a+b 为
( )
A.1 B.0 C.-1 D. 1
答案 A
7.(四川省绵阳市 2010 年 4 月高三三诊文科试题)函数 y= xa 与 x
ay )1( (a>0,且 a≠1)的图象关于( B )
(A)x 轴对称 (B)y 轴对称
(C)原点对称 (D)直线 y=x 对称
8.(四川省雅安市 2010 届高三第三次诊断性考试文科)函数 2 1 ( 0)y x x 的反函数是
( A )
A. 1 ( 1)y x x B. 1 ( 0)y x x
C. 1 ( 1)y x x D. 1 ( 0)y x x
9.(四川省自贡市 2010 届高三三诊文科试题)函数 ( 0)y x x 的反函数是( A )
A. 2 ( 0)y x x B. 2 ( 0)y x x
C. 2 ( 0)y x x D. 2 ( 0)y x x
10.(四川省南充高中 2010 届高三 4 月月考理科试题)在 y=2x,y=log2x,y=x2,y=cos2x 这四个函数
中,当 0<x1<x2<1,使
2
)()()2( 2121 xfxfxxf 恒成立的函数的个数是( B )
A.0 B.1 C.2 D.3
11.(四川省泸州市 2010 届高三第二次教学质量诊断性考试文科)函数 3log ( 0)y x x 的反函数为( C )
A. 3 ( 0)xy x B. 1 ( )3
x
y x R
C. 3 ( )xy x R D. 1 ( 0)3
x
y x
12.(广东省惠州市 2010 届高三第三次调研文科)方程 22 3x x 的实数解的个数为( )
A.2 B.3 C.1 D.4
【答案】A
13.(四川省雅安市 2010 届高三第三次诊断性考试理科)
已知函数 2 ( 0)( )
1 ( 0)
a b xf x x x x
x x
在 R 上连续,则 a b ( A )
A.2 B.1 C.0 D. 1
14.(四川省自贡市 2010 届高三三诊理科试题)已知函数 3 21
3y x x x 的图象 C 上存在一个定点 P 满
足:若过定点 P 的直线l 与曲线 C 交于不同于 P 的两点 1 1( , )M x y , 2 2( , )N x y ,就恒有 1 2y y 为定值 0y ,
则 0y 的值为( B )
A. 1
3
B. 2
3
C. 4
3
D. 2
15.(四川省资阳市 2009—2010 学年度高三第三次高考模拟理)已知命题 p:函数 ( ) | |f x x a 在 (1, )+¥
上是增函数,命题 q: ( ) xf x a ( 0a 且 1a )是减函数,则 p 是 q 的( A )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分也不必要条件
16.(四川省泸州市 2010 届高三第二次教学质量诊断性考试理科)设方程 2 lgx x 的两个根为 1 2,x x ,
则下列关系正确的是( A )
A. 1 20 1x x B. 1 2 1x x C. 1 2 1x x D. 1 2 0x x
17.(四川省泸州市 2010 届高三第二次教学质量诊断性考试理科)设定义在 R 上的函数 ( )f x ,
(0) 2008f ,且对任意 x R ,满足 ( 2) ( ) 3 2 xf x f x , ( 6) ( ) 63 2 xf x f x ,则 (2008)f
下列关系正确的是( D )
A. 20052 2004 B. 20072 2006 C. 20092 2008 D. 20082 2007
18 . ( 四 川 省 成 都 市 石 室 中 学 2010 届 高 三 三 诊 模 拟 理 科 ) 定 义 在 [0 , 1] 上 的 函 数 )(xf 满 足
)(2
1)5(,1)1()(,0)0( xfxfxfxff ,且当 10 21 xx 时,
)2010
1().()( 21 fxfxf 则 等于 ( C )
A.
2
1 B.
16
1 C.
32
1 D.
64
1
19.(广东省惠州市 2010 届高三第三次调研理科)给出定义:若函数 ( )f x 在 D 上可导,即 ( )f x 存在,且
导函数 ( )f x 在 D 上也可导,则称 ( )f x 在 D 上存在二阶导函数,记 ( )f x f x ,若 ( ) 0f x 在 D
上恒成立,则称 ( )f x 在 D 上为凸函数。以下四个函数在 0, 2
上不是凸函数的是( )
A. ( ) sin cosf x x x B. ( ) ln 2f x x x
C. 3( ) 2 1f x x x D. ( ) xf x xe
20.(四川省绵阳市 2010 年 4 月高三三诊理科试题)已知函数 )(xf (x∈R) 导函数 )(xf 满足 )()( xfxf ,则
当 a>0 时, )(af 与 )0(fea 之间的大小关系为( A)
(A) )(af < )0(fea (B) )(af > )0(fea
(C) )(af = )0(fea (D)不能确定,与 )(xf 或 a 有关
21.(四川省成都市 2010 届高三第三次诊断理科)设函数 f(x)=x2+2(-2≤x<0),其反函数为 f-1(x),则
f-1(3)=( )
(A)-1 (B)1 (C)0 或 1 (D)1 或-1
【答案】A
【解析】令 f(t)=3,则 t=f-1(3) (-2≤t<0)
有 t2+2=3 t=±1
但-2≤t<0,故 t=-1
22.(2010 年广东省揭阳市高考一模试题文科)过曲线 2
1xy x
( 0x )上横坐标为 1 的点的切线方程
为
A. 3 1 0x y B. 3 5 0x y C. 1 0x y D. 1 0x y
【答案】B
【 解 析 】
2 2
4 4
2 ( 1) 2' x x x x xy x x
∴ 该 切 线 的 斜 率 1'| 3xk y 故 所 求 的 切 线 方 程 为
2 3( 1)y x ,即3 5 0x y ,故选 B.
23.(四川省绵阳市 2010 年 4 月高三三诊文科试题)函数 f (x)=ax3+2x+1(a≠0)在 x=1 处的切线方程为
x+y-2=0,则实数 a=( B )
(A)1 (B)-1 (C)-2 (D)3
24.(四川省成都市石室中学 2010 届高三三诊模拟理科)已知 )2('),1('3)( 2 fxfxxf 则 =( A )
A.1 B.2 C.4 D.8
25.(2010 年 3 月广东省深圳市高三年级第一次调研考试文科)
已知函数 f x( )的导函数 2f x ax bx c ( ) 的图象如右图,
则 f x( )的图象可能是( D )
二、填空题
26.(四川省成都市 2010 届高三第三次诊断理科)如果函数 f(x)同时满足下列条件:①在闭区间[a,b]内连续,
x
o
y
②在开区间(a,b)内可导且其导函数为 f'(x),那么在区间(a,b)内至少存在一
点ξ(a<ξ<b),使得 f(b)-f(a)=f'(ξ)(b-a)成立,我们把这一规律称为函数 f(x)在区间(a,b)内具有“Lg”性
质,并把其中的ξ称为中值。有下列命题:
①若函数 f(x)在(a,b)具有“Lg”性质,ξ为中值,点 A(a,f(a)),B(b,f(b)),则直线 AB 的斜率为 f'(ξ);
②函数 y=
2
2 2
x 在(0,2)内具有“Lg”性质,且中值ξ= 2 ,f'(ξ)=- 2
2
;
③函数 f(x)=x3 在(-1,2)内具有“Lg”性质,但中值ξ不唯一;
④若定义在[a,b]内的连续函数 f(x)对任意的 x1、x2∈[a,b],x1<x2,有 1
2 [f(x1)+f(x2)]<f( 1 2
2
x x
)恒成立,
则函数 f(x)在(a,b)内具有“Lg”性质,且必有中值ξ= 1 2
2
x x
.
其中你认为正确的所有命题序号是___________________.
答案 ①②
解析:对于①,根据导函数的几何意义立即可得正确;
对于②,函数 y 在(0,2)上连续且可导,代值计算可得两端点连线的斜率为- 2
2
又 y'=
12
21 (2 ) ( )2 2
x x
,当 x= 2 时,y'=- 2
2
,故②正确。
对于③,两端点连线斜率为 3
而 f'(x)=3x2,令 3x2=3 x=±1,在(-1,2)内只有一个中值ξ=1,故③错误;
对于④, 1
2 [f(x1)+f(x2)]<f( 1 2
2
x x
)只能保证 f(x)是上凸函数,不能保证中值一定在中点处。④错误
27.(四川省雅安市 2010 届高三第三次诊断性考试理科)给出下列四个函数:① 2( ) 1f x x ;②
( ) lnf x x ; ③ ( ) xf x e ; ④ ( ) sinf x x 其 中 满 足 :“ 对 任 意 1 2 1 2, (1,2)( )x x x x , 都 有
1 2 1 2| ( ) ( ) | | |f x f x x x ”的函数序号是 。 (②③④)
28.(四川省自贡市 2010 届高三三诊理科试题)有下列命题:
① a b 是 2 2a b 的充分不必要条件;
② 2 2 21 ( )2OP OQ OP OQ PQ ;
③若函数 ( )f x 满足 ( 1) 1 ( )f x f x ,则 ( )f x 是周期函数;
④如果一组数据中,每个数都加上同一个非零常数 c,则这组数据的平均数和方差都改变。
其中错误命题的序号为 (要求填写所有错误命题的序号)。 (①④)
29.(四川省绵阳市 2010 年 4 月高三三诊理科试题)若函数 f (x) =ax(a>0 且 a≠1)的反函数为 y= )(1 xf ,
且 )2
1(1f =2,则 f (-2)= 2 .
30.(四川省南充高中 2010 届高三 4 月月考理科试题)已知函数
x
x
xf
3
log
)( 2 ,
则
)4
1(ff 的值为_____________ (
9
1 )
31.(2010 年广东省揭阳市高考一模试题文科)若函数 ( ) logmf x x 的反函数的图象过点 ( 1, )n ,则
mn 3 的最小值是
A. 22 B.2 C. 32 D.
2
5
【答案】C
【 解 析 】 由 函 数 ( ) logmf x x 的 反 函 数 的 图 象 过 点 ( 1, )n 得 原 函 数 的 图 象 过 点 ( , 1)n , 即
1log nm 0, 0, 1m n mn ,由均值不等式得3n m 2 3 2 3mn ,当且仅当3n m 时取等
号,故选 C.
32.(四川省绵阳市 2010 年 4 月高三三诊文科试题)若函数 f (x)= ax 的反函数为 y= )(1 xf ,且 )2(1f =1,
则 f (2)= ________ ( 5 )
33.(四川省成都市 2010 届高三第三次诊断文科)关于 x 的方程 x2+2ax-4=0 的两个实根 x1、x2 满足
x1<1<x2,则实数 a 的取值范围是_____________.
答案:(-∞, 3
2)
解析:记 f(x)=x2+2ax-4
则函数 f(x)的图象与 x 轴的两个交点分别在 1 的两侧
注意到 f(x)开口向上,
故 f(1)<0 a<
34.(四川省绵阳市 2010 年 4 月高三三诊理科试题)若对任意 x∈R,y∈R 有唯一确定的 f (x,
y)与之对应,则称 f (x,y)为关于 x,y 的二元函数.
定义:同时满足下列性质的二元函数 f (x,y)为关于实数 x,y 的广义“距离”:
(Ⅰ)非负性:f (x,y)≥0;
(Ⅱ)对称性:f (x,y)= f (y,x);
(Ⅲ)三角形不等式:f (x,y)≤f (x,z)+ f (z,y)对任意的实数 z 均成立.
给出下列二元函数:
①f (x,y)=(x-y)2;②f (x,y)=|x-y|;③f (x,y)= yx ;④f (x,y)=|sin(x-y)|.
则其中能够成为关于 x,y 的广义“距离”的函数编号是________.(写出所有真命题的序号)(②④)
35.(四川省攀枝花市 2010 年 4 月高三第二次统考文科试题)已知 ( )f x 是以 2 为周期的偶
函数,当 0,1 , ( )x f x x ,那么在区间 1,3 内,关于 x 的方程 4 ( )f x x m (其中 m 为实常数)
有四个不同的实根,则 m 的取值范围是 . ]1,0(
(x>0)
(x≤0)
36.(广东省惠州市 2010 届高三第三次调研文科)已知 2( ) 3 (2), (2)f x x xf f 则 = .
【解析】 ' '( ) 2 3 (2)f x x f , ' ' '(2) 2 2 3 (2), (2) 2f f f .填 2
三、解答题
37.(四川省资阳市 2009—2010 学年度高三第三次高考模拟理)(本小题满分 12 分)
已知定义在 (0, ) 上的三个函数 ( ) lnf x x , 2( ) ( )g x x af x , ( )h x x a x ,且 ( )g x 在 1x 处取得极
值.
(Ⅰ)求 a 的值及函数 ( )h x 的单调区间;
(Ⅱ)求证:当 21 x e 时,恒有 2 ( )
2 ( )
f xx f x
成立;
(Ⅲ)把 ( )h x 对应的曲线 C1 向上平移 6 个单位后得曲线 C2,求 C2 与 ( )g x 对应曲线 C3 的交点个数,并
说明理由.
解:(Ⅰ) 2 2( ) ( ) lng x x af x x a x , ( ) 2 ag x x x
, (1) 2 0g a ,∴ 2a . 2 分
而 ( ) 2h x x x , 1( ) 1h x
x
,令 1( ) 1 0h x
x
得 1x ;令 1( ) 1 0h x
x
得 0 1x .∴函数 ( )h x
单调递增区间是 (1, ) ;单调递减区间是 (0,1) . 4 分
(Ⅱ)∵ 21 x e ,∴ 0 ln 2x ,∴ 2 ln 0x ,
欲证 2 ( )
2 ( )
f xx f x
,只需要证明 [2 ( )] 2 ( )x f x f x ,即证明 2( 1)( ) 1
xf x x
,6 分
记 2( 1) 2( 1)( ) ( ) ln1 1
x xk x f x xx x
,∴
2
2
( 1)( ) ( 1)
xk x x x
,
当 1x 时, ( ) 0k x ,∴ ( )k x 在 (1, ) 上是增函数,
∴ ( ) (1) 0k x k ,∴ ( ) 0k x ,即 2( 1)ln 01
xx x
,
∴ 2( 1)ln 1
xx x
,故结论成立.8 分
(Ⅲ)由(Ⅰ)知 2( ) 2lng x x x , ( ) 2h x x x ,∴C2 对应的表达式为 1( ) 2 6h x x x ,问题转化
为求函数 2( ) 2lng x x x 与 1( ) 2 6h x x x 图象交点个数.
故只需求方程 2 2ln 2 6x x x x ,即 22 2ln 6x x x x 根的个数. 10 分
设 2 ( ) 2 2lnh x x x , 2
3 ( ) 6h x x x ,
2
1 2 ( 2) 2( ) x x xh x x xx x x
.当 (0,4)x 时, 2 ( ) 0h x , 2 ( )h x
为 减 函 数 ; 当 (4, )x 时 , 2 ( ) 0h x , 2 ( )h x 为 增 函 数 . 而
2 2
3
1 25( ) 6 ( )2 4h x x x x ,图象是开口向下的抛物线.作出函数 2 ( )h x 与 3 ( )h x 的图
象, 3
1 25( )2 4h ,而 2 2
1 1 1( ) 2 2 ln 2 2 ln 2 ( )2 2 2h h 可知交点个数为 2 个,即曲线 C2 与 C3 的交
点个数为 2 个. 12 分
38.(四川省绵阳市 2010 年 4 月高三三诊理科试题)(本小题满分 14 分)
已知函数 f (x)=ln(1+x)-ax 的图象在 x=1 处的切线与直线 x+2y-1=0 平行.
(Ⅰ)求实数 a 的值;
(Ⅱ)若方程 f (x)= )3(4
1 xm 在[2,4]上有两个不相等的实数根,求实数 m 的取值范围;(参考数据:e=2.71
828…)
(Ⅲ)设常数 p≥1,数列{an}满足 )ln(1 nnn apaa (n∈N*),a1=lnp,
求证: 1na ≥ na .
∴ g(2)-1)有
x
x
xxf
111
1)( ,
显然 )0(f 0,当 x∈(0,+∞)时, 0)( xf ,当 x∈(-1,0)时, 0)( xf ,
∴ f (x)在(-1,0)上是增函数,在 ,0 上是减函数.
∴ f (x)在(-1,+∞)上有最大值 f (0),而 f (0)=0,
∴ 当 x∈(-1,+∞)时,f (x)≤0,因此 ln(1+x)≤x.(*)…………………11 分
由已知有 p>an,即 p-an>0,所以 p-an-1>-1.
∵ an+1-an=ln(p-an)=ln(1+p-1-an),
∴ 由(*)中结论可得 an+1-an≤p-1-an,即 an+1≤p-1 (n∈N*).
∴ 当 n≥2 时, 1na -an=ln(p-an)≥ln[p-(p-1)]=0,即 1na ≥an.
当 n=1,a2=a1+ln(p-lnp),
∵ lnp=ln(1+p-1)≤p-1,
∴ a2≥a1+ln[p-(p-1)]=a1,结论成立.
∴ 对 n∈N*,an+1≥an.………………………………………………………14 分
39.(四川省自贡市 2010 届高三三诊理科试题)(本小题满分 12 分)
已知函数 2( ) 2lnf x x x 。
(I)若方程 ( ) 0f x m 在 1[ , ]ee
内有两个不等的实根,求实数 m 的取值范围( e 为自然对数的底);
(II)如果函数 ( ) ( )g x f x ax 的图象与 x 轴交于两点 1( ,0)A x , 2( ,0)B x ,且 1 20 x x 。求证:
1 2'( ) 0g px qx (其中正常数 p 、 q 满足 1,p q q p )。
解:(Ⅰ)由 ( )f x =2 2ln xx 求导得到: ( )f x =
x
xx )1)(1(2 , …………(2 分)
],1[ eex ,故 ( )f x =0 在 1x 有唯一的极值点, )1(ef =-2- 2
1
e
)(ef =―2― 2e , )(xf 极大值= )1(f =-1, …………(4 分)
且知 )(ef < )1(ef ,故 )(xf =- m ,在 ],1[ ee
内有两个不等的实根满足:
-2- 2
1
e
≤- m <-1 故 m 的取值范围为
2
12,1
e
…………(6 分)
(Ⅱ) ( )g x =
x
2 -2 x - a ,又 ( )f x - ax =0 有两个不等的实根 1x 、 2x ,则
0ln2
0ln2
2
2
22
1
2
11
axxx
axxx 两式相减得到
21
21 )ln(ln2
xx
xxa )( 21 xx …………(7 分)
于是
'g )( 21 qxpx = 22
21
qxpx )( 21 qxpx -[
21
21 )ln(ln2
xx
xx )( 21 xx ]
= 21
2
qxpx 21
21 )ln(ln2
xx
xx
+ )12( p )( 12 xx
∵ 2 p ≤1, 012 xx , ∴ )12( p )( 12 xx ≤0 …………(8 分)
要证: 'g )( 21 qxpx <0,只需证:
21
2
qxpx +
12
21 )ln(ln2
xx
xx
<0,只需证:
0ln
2
1
21
12
x
x
qxpx
xx ① ………(9 分)
令 tx
x
2
1 ,0 1 t ,只需证:
qpt
ttu
1)( + 0ln t 在 10 t 上恒成立,
又∵ 2)(
11)('
qptttu
=
2
2
2
2
)(
))(1(
qptt
p
qttp
………(10 分)
∵ 1 qp ,
2
1q ,则 1
p
q ,∴ 12
2
p
q ,于是由 1t 可知 01 t , 02
2
p
qt
故知 0)(' tu ∴ )(tu 在 )1,0(t 上为增函数, ………(11 分)
则 )(tu < )1(u =0,从而知 0ln
2
1
21
12
x
x
qxpx
xx
即①成立,从而原不等式成立。 …………(12 分)
40.(四川省攀枝花市2010年4月高三第二次统考文科试题)(12分)已知函数 2( ) 1 ,f x ax bx a b R .
(Ⅰ)若 ( 1) 0f 且对任意实数 x 均有 ( ) 0f x 成立,求实数 ,a b 的值;
(Ⅱ)在(Ⅰ)的条件下,当 2,2x 时, ( ) ( )g x f x kx 是单调函数,求实数 k 的取值范围.
解:(Ⅰ) ( 1) 0 1 0 1f a b b a 即
又对任意实数 x 均有 )(xf 0 成立
2 4 0b a 恒成立,即 2( 1) 0a 恒成立
1, 2a b
(Ⅱ)由(Ⅰ)可知 2 2( ) 2 1 ( ) (2 ) 1f x x x g x x k x
( )g x 在 x [-2,2]时是单调函数, 2 2[ 2,2] ( , ] [ 2,2] [ , )2 2
k k 或
2 22 22 2
k k 或 即实数 k 的取值范围为 ( , 2] [6, )
41.(四川省攀枝花市 2010 年 4 月高三第二次统考文科试题)(14 分)已知定义在 R 上的函数
2( ) ( 3)f x x ax ,其中 a 为常数.
(Ⅰ)若 1x 是函数 ( )f x 的一个极值点,求 a 的值;
(Ⅱ)若函数 ( )f x 在区间 1,0 上是增函数,求 a 的取值范围;
(Ⅲ)若函数 ( ) ( ) ( ), 0,2g x f x f x x ,在 0x 处取得最大值,求正数 a 的取值范围.
解:(Ⅰ) 3 2 2( ) 3 , ( ) 3 6 3 ( 2).f x ax x f x ax x x ax
)(1 xfx 是 的一个极值点, (1) 0, 2f a ;
(Ⅱ)①当 a=0 时, 23)( xxf 在区间(-1,0)上是增函数, 0a 符合题意;
②当
axxxfaxaxxfa 2,0:0)(),2(3)(,0 21 得令时 ;
当 a>0 时,对任意 0,0)(),0,1( axfx 符合题意;
当 a<0 时,当 02,12,0)()0,2( aaxfax 时 符合题意;
综上所述, .2a
(Ⅲ) ].2,0[,6)33()(,0 23 xxxaaxxga
],2)1(2[36)33(23)( 22 xaaxxaaxxg
令 .044(*),02)1(2,0)( 22 axaaxxg 显然有即
42.(四川省成都市石室中学 2010 届高三三诊模拟理科)(12 分)
已知 .)2()(,0 2 xeaxxxfa 函数
(1)当 x 为何值时, )(xf 取得最小值?证明你的结论;
(2)设 f(x)在[-1,1]上是单调函数,求 a 的取值范围。
解:(1)对函数 )(xf 求导数得 xeaaxxxxf )222()(' 2
令 02)1(20]2)1(2[,0)(' 22 axaxeaxaxxf x 从而得
解得 11,11 2
2
2
1 aaxaax
当 x 变化时, )('),( xfxf 的变化如下表[来
x ),( 1x 1x ),( 21 xx 2x [ ),( 2 x
)(' xf + 0 - 0 +
)(xf 递增 极大值 递减 极小值 递增
1)( xxxf 在 处取得极大值,在 x=x2 处取得极小值。
当 0a 时, ),()(,0,1 2121 xxxfxx 在 上为减函数,在 ),( 2 x 上为增函数
而当 0)2()(0 xeaxxxfx 时 ,
当 x=0 时, 0)( xf
所以当 11 2 aax 时,f(x)取得最小值
(II)当 0a 时, ]1,1[)( 在xf 上为单调函数的充要条件是 12 x
即
4
3,111 2 aaa 解得
于是 )(xf 在[-1,1]上为单调函数的充要条件是
4
3a
即 a 的取值范围是
,4
3
43.(2010 年 3 月广东省广州市高三一模数学理科试题)(本小题满分 14 分)
已知 aR ,函数 ( ) ln 1af x xx
, ( ) ln 1 xg x x e x (其中 e 为自然对数的底数).
(1)求函数 ( )f x 在区间 0,e 上的最小值;
(2)是否存在实数 0 0,x e ,使曲线 ( )y g x 在点 0x x 处的切线与 y 轴垂直? 若存在,求出 0x 的值;
若不存在,请说明理由.
解
[
此时 ( )f x 在区间 0,e 上的最小值为 ln1 0 ,即 1 ln 1 0xx
≥ .
当 0 0,x e , 0 0xe , 0
0
1 ln 1 0xx
≥ ,
∴ 0
0 0
0
1( ) ln 1 1 1 0xg x x ex
≥ .
曲线 ( )y g x 在点 0x x 处的切线与 y 轴垂直等价于方程 0( ) 0g x 有实数解.
而 0 0g x ,即方程 0( ) 0g x 无实数解.
故不存在 0 0,x e ,使曲线 ( )y g x 在点 0x x 处的切线与 y 轴垂直.
44.(2010 年 3 月广东省广州市高三一模数学文科试题)(本小题满分 14 分)
已知函数 3 2f x x ax bx c 在 ,0 上是减函数,在 0,1 上是增函数,函数 f x 在 R 上有三
个零点,且 1 是其中一个零点.
(1)求b 的值;
(2)求 2f 的取值范围;
(3)试探究直线 1y x 与函数 y f x 的图像交点个数的情况,并说明理由.
解
(1)解:∵ 3 2f x x ax bx c ,∴ 23 2f x x ax b .
∵ f x 在 ,0 上是减函数,在 0,1 上是增函数,
∴当 0x 时, f x 取到极小值,即 0 0f .
∴ 0b .
(2)解:由(1)知, 3 2f x x ax c ,
∵1 是函数 f x 的一个零点,即 1 0f ,∴ 1c a .
∵ 23 2 0f x x ax 的两个根分别为 1 0x , 2
2
3
ax .
∵ f x 在 0,1 上是增函数,且函数 f x 在 R 上有三个零点,
∴ 2
2 13
ax ,即 3
2a .
∴ 52 8 4 1 3 7 2f a a a .
故 2f 的取值范围为 5 ,2
.
(3)解:由(2)知 3 2 1f x x ax a ,且 3
2a .
要讨论直线 1y x 与函数 y f x 图像的交点个数情况,
即求方程组 3 2
1,
1
y x
y x ax a
解的个数情况.
由 3 2 1 1x ax a x ,
得 3 21 1 1 0x a x x .
即 21 1 1 1 1 0x x x a x x x .
即 21 1 2 0x x a x a .
∴ 1x 或 2 1 2 0x a x a .
由方程 2 1 2 0x a x a , (*)
得 2 21 4 2 2 7a a a a .
∵ 3
2a ,
若 0 ,即 2 2 7 0a a ,解得 3 2 2 12 a .此时方程(*)无实数解.
若 0 ,即 2 2 7 0a a ,解得 2 2 1a .此时方程(*)有一个实数解 2 1x .
若 0 , 即 2 2 7 0a a , 解 得 2 2 1a . 此 时 方 程 ( * ) 有 两 个 实 数 解 , 分 别 为
2
1
1 2 7
2
a a ax ,
2
2
1 2 7
2
a a ax .
且当 2a 时, 1 0x , 2 1x .
综上所述,当 3 2 2 12 a 时,直线 1y x 与函数 y f x 的图像有一个交点.
当 2 2 1a 或 2a 时,直线 1y x 与函数 y f x 的图像有二个交点.
当 2 2 1a 且 2a 时,直线 1y x 与函数 y f x 的图像有三个交点.