- 2021-05-23 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考专项复习
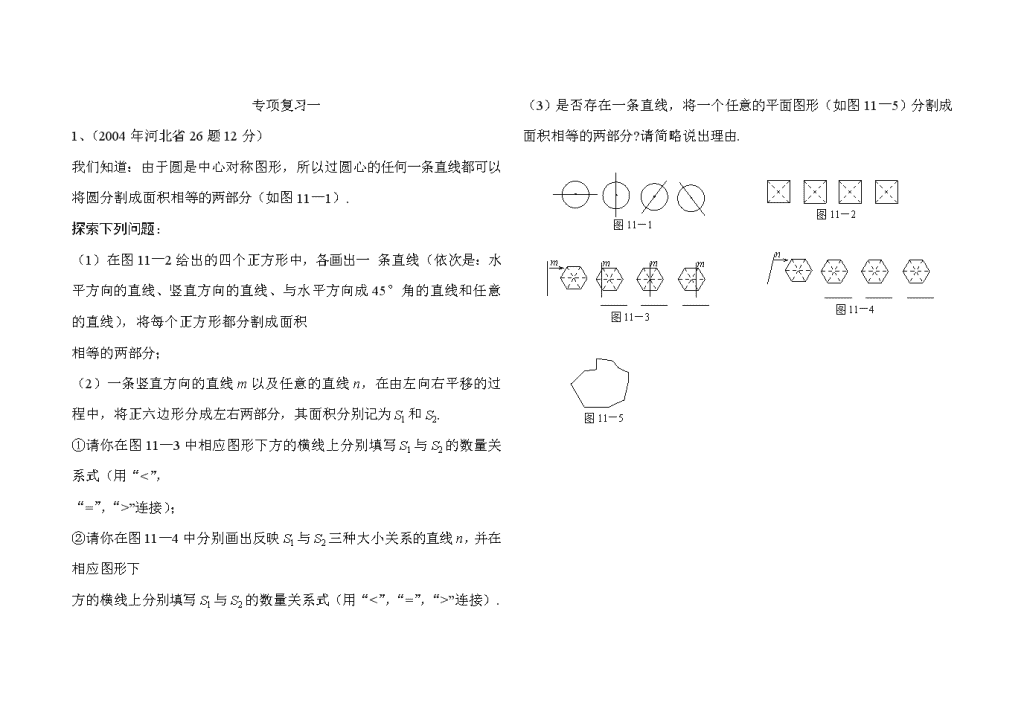
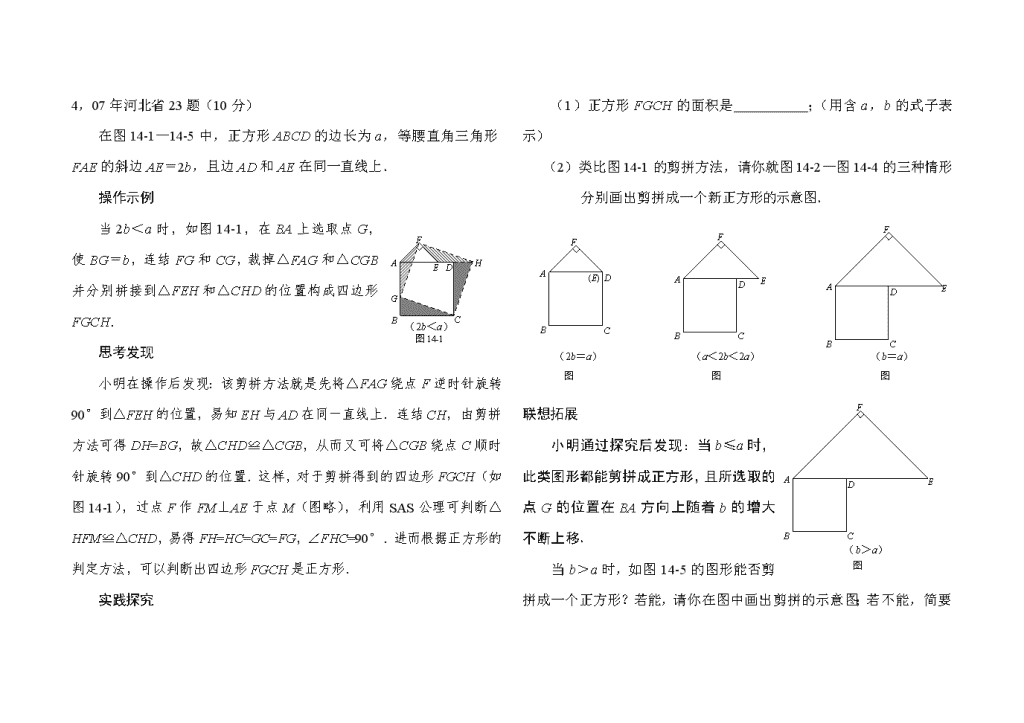
专项复习一 1、(2004年河北省26题12分) 我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图11—1). 探索下列问题: (1)在图11—2给出的四个正方形中,各画出一 条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积 相等的两部分; (2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2. ①请你在图11—3中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”, “=”,“>”连接); ②请你在图11—4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下 方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接). (3)是否存在一条直线,将一个任意的平面图形(如图11—5)分割成面积相等的两部分?请简略说出理由. n 图11—4 m m m m 图11—3 图11—1 图11—2 图11—5 2、(2003年河北省26题12分) 探究规律:如图1,已知直线∥,A、B为直线上的两点,C、P为直线上的两点。 (1)请写出图中面积相等的各对三角形: 。 (2)如果A、B、C为三个定点,点P在上移动,那么无论P点移动到任何位置总有: 与△ABC的面积相等;理由是: 。 解决问题: 如图2,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但承包土地与开垦荒地的分界小路(图3中折线CDE)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多。请你用有关的几何知识,按张大爷的要求设计出修路方案。(不计分界小路与直路的占地面积) (1)写出设计方案,并在图3中画出相应的图形; (2)说明方案设计理由。 图12-1 A B C D 3,06年河北省22题。 探索 A B C D E 图12-2 在如图12-1至图12-3中,△ABC的面积为a . (1)如图12-1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示); (2)如图12-2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含a的代数式表示),并写出理由; D E A B C F 图12-3 (3)在图12-2的基础上延长AB到点F,使BF=AB,连结FD, FE,得到△DEF(如图12-3).若阴影部分的面积为S3, 则S3=__________(用含a的代数式表示). 发现 图12-4 D E A B C F H M G 像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图12-3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_______倍. 应用 去年在面积为10m2的△ABC空地上栽种了某种花卉.今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH(如图12-4).求这两次扩展的区域(即阴影部分)面积共为多少m2? 4,07年河北省23题(10分) 在图14-1—14-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上. 操作示例 当2b<a时,F 图14-1 A B C E D H G (2b<a) 如图14-1,在BA上选取点G,使BG=b,连结FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH. 思考发现 小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连结CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图14-1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形. 实践探究 (1)正方形FGCH的面积是 ;(用含a,b的式子表示) (2)类比图14-1的剪拼方法,请你就图14-2—图14-4的三种情形分别画出剪拼成一个新正方形的示意图. 图14-3 F A B C D E 图14-4 F A B C D E 图14-2 F A B C (E) D (2b=a) (a<2b<2a) (b=a) F 图14-5 A B C E D (b>a) 联想拓展 小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移. 当b>a时,如图14-5的图形能否剪拼成一个正方形?若能, 请你在图中画出剪拼的示意图;若不能,简要说明理由. 5,.(08河北)(本小题满分10分) 在一平直河岸同侧有两个村庄,到的距离分别是3km和2km, .现计划在河岸上建一抽水站,用输水管向两个村庄供水. 方案设计 某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中管道长度为,且(其中于点);图13-2是方案二的示意图,设该方案中管道长度为,且(其中点与点关于对称,与交于点). A B P l l A B P C 图13-1 图13-2 l A B P C 图13-3 K 观察计算 (1)在方案一中, km(用含的式子表示); (2)在方案二中,组长小宇为了计算的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算, km(用含的式子表示). 探索归纳 (1)①当时,比较大小:(填“>”、“=”或“<”); ②当时,比较大小:(填“>”、“=”或“<”); (2)请你参考右边方框中的方法指导, 就(当时)的所有取值情况进 行分析,要使铺设的管道长度较短, 应选择方案一还是方案二? 方法指导 当不易直接比较两个正数与的大小时,可以对它们的平方进行比较: ,, 与的符号相同. 当时,,即; 当时,,即; 当时,,即; 6,(09年河北省23题满分10分) 如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c. 阅读理解: 图13-1 A O1 O O2 B B 图13-2 A C n° D O1 O2 B 图13-3 O2 O3 O A O1 C O4 (1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到 ⊙O2的位置,当AB = c时,⊙O恰好自转1周. (2)如图13-2,∠ABC相邻的补角是n°,⊙O在 ∠ABC外部沿A-B-C滚动,在点B处,必须由 ⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋 转的角∠O1BO2 = n°,⊙O在点B处自转周. 实践应用: (1)在阅读理解的(1)中,若AB = 2c,则⊙O自 转 周;若AB = l,则⊙O自转 周.在 阅读理解的(2)中,若∠ABC = 120°,则⊙O 在点B处自转 周;若∠ABC = 60°,则⊙O 在点B处自转 周. (2)如图13-3,∠ABC=90°,AB=BC=c.⊙O从 ⊙O1的位置出发,在∠ABC外部沿A-B-C滚动 到⊙O4的位置,⊙O自转 周. O A B C 图13-4 D 拓展联想: (1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由. (2)如图13-5,多边形的周长为l,⊙O从与某边相切于 点D的位置出发,在多边形外部,按顺时针方向沿多 边形滚动,又回到与该边相切于点D的位置,直接写 D 图13-5 O 出⊙O自转的周数. 7标签:面积,正方形,特殊到一般 已知正方形ABCD的边长为4,G是边CD上一点,以CG为一边作正方形GCEF (1) 如图1,当点G与点D重合时,△BDF的面积为 (2) 如图2,当点G是CD的中点时,△BDF的面积为 (1) 如图3,当点G在CD边上的任意位置时,△BDF的面积为 解决问题: 农民李大伯有一块正方形的土地ABCD(如图4),由于修路被占去一块三角形土地BCP,现决定在DP的右侧补给李大伯一块土地,补偿后的土地为四边形ABMD,四边形ABMD的面积与原来正方形ABCD的面积相等,且M在射线BP上。请你在图4中画出点M的位置,并简要说明理由。 A B C E F D(G) 图1 B C E F D A G 图2 D A B C E F G 图3 P D A B C 图4 8标签:面积,三角形中线,四边形,特殊到一般 如图1,在△ABC中,AD为BC边上的中线,则S△ABD=S△ADC,由这个结论解答下列问题。 (1) 在图2中,点E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为 在图3中,点E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和SABCD之间满足的关系式为 (2)在图4中,点E、F分别为任意四边形ABCD边AD、BC的中点,则S阴和SABCD之间满足的关系式为 (3)如图5中,点E、F、G、H分别为任意四边形的四条边AD、AB、BC、CD的中点,并且图中四个小三角形的面积和为1,既S1+S2+S3+S4=1,求S阴的值。(中间小四边形为阴影) 图5 S2 G B D A E H C F S1 S4 D C B A E F 图2 F C D E B A 图4 图1 A D C B 图3 F E D C B A S3查看更多