2015东营市中考数学试题与答案

2015东营市中考数学试题与答案

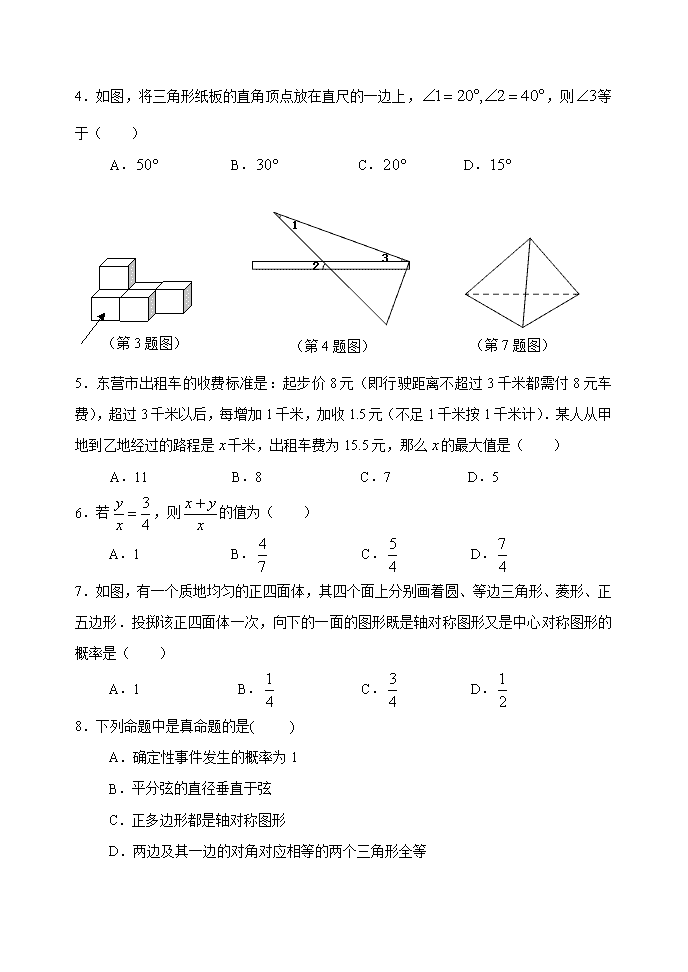
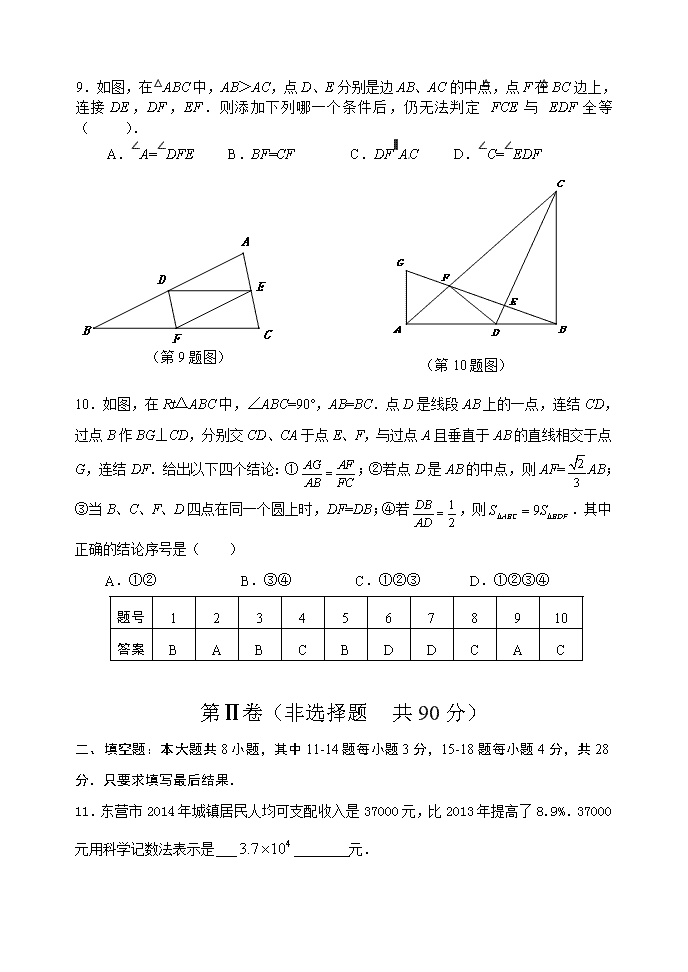
秘密★启用前 试卷类型：A 二0一五年东营市初中学生学业考试 数 学 试 题 ‎（总分120分 考试时间120分钟） ‎ 注意事项：‎ ‎1．本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，30分；第Ⅱ卷为非选择题，90分；全卷共8页．‎ ‎2．数学试题答题卡共8页．答题前，考生务必将自己的姓名、考号、考试科目等涂写在试题和答题卡上，考试结束，试题和答题卡一并收回．‎ ‎3．第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．第Ⅱ卷按要求用‎0.5mm碳素笔答在答题卡的相应位置上.‎ ‎4．考试时，不允许使用科学计算器．‎ 第Ⅰ卷（选择题 共30分） ‎ 一、选择题：本大题共10小题，在每小题给出的四个选项中，只有一项是正确的,请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分． ‎ ‎1．的相反数是（ ）‎ A． B． C． D．‎ ‎2．下列计算正确的是（ ）‎ A． B． ‎ C． D．‎ ‎3．由六个小正方体搭成的几何体如图所示，则它的主视图是（ ）‎ A． B． C． D．‎ ‎4．如图，将三角形纸板的直角顶点放在直尺的一边上，，则等于（ ）‎ A． B． C． D．‎ ‎（第4题图）‎ ‎（第7题图）‎ ‎（第3题图）‎ ‎5．东营市出租车的收费标准是：起步价8元（即行驶距离不超过‎3千米都需付8元车费），超过‎3千米以后，每增加‎1千米，加收1.5元（不足‎1千米按‎1千米计）．某人从甲地到乙地经过的路程是千米，出租车费为15.5元，那么的最大值是（ ）‎ A．11 B．‎8 C．7 D．5‎ ‎6．若，则的值为（ ）‎ A．1 B． C． D．‎ ‎7．如图，有一个质地均匀的正四面体，其四个面上分别画着圆、等边三角形、菱形、正五边形．投掷该正四面体一次，向下的一面的图形既是轴对称图形又是中心对称图形的概率是（ ）‎ A．1 B． C． D．‎ ‎8．下列命题中是真命题的是( )‎ A．确定性事件发生的概率为1‎ B．平分弦的直径垂直于弦 C．正多边形都是轴对称图形 D．两边及其一边的对角对应相等的两个三角形全等 ‎9．如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE，DF，EF．则添加下列哪一个条件后，仍无法判定△FCE与△EDF全等（ ）．‎ A．∠A=∠DFE B．BF=CF C．DF∥AC D．∠C=∠EDF ‎（第10题图）‎ ‎（第9题图）‎ ‎10．如图，在Rt△ABC中，∠ABC=90°，AB=BC．点D是线段AB上的一点，连结CD，过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连结DF．给出以下四个结论：①；②若点D是AB的中点，则AF=AB；③当B、C、F、D四点在同一个圆上时，DF=DB；④若，则．其中正确的结论序号是（ ）‎ A．①② B．③④ C．①②③ D．①②③④‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B A B C B D ‎ D ‎ C A C 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共8小题，其中11-14题每小题3分，15-18题每小题4分，共28分．只要求填写最后结果．‎ ‎11．东营市2014年城镇居民人均可支配收入是37000元，比2013年提高了8.9%．37000元用科学记数法表示是 元．‎ ‎12．分解因式： ．‎ ‎13．在一次数学测验中，随机抽取了10份试卷，其成绩如下：85，81，89，81，72，82，77，81，79，83．则这组数据的中位数为 81 ．‎ ‎（第14题图）‎ ‎14．‎4月26日，2015黄河口（东营）国际马拉松比赛拉开帷幕，中央电视台体育频道用直升机航拍技术全程直播．如图，在直升机的镜头下，观测马拉松景观大道A处的俯角为，B处的俯角为．如果此时直升机镜头C处的高度CD为‎200米，点A、D、B在同一直线上，则AB两点的距离是 米．‎ ‎15．如图，水平放置的圆柱形排水管道的截面直径是‎1m，其中水面的宽AB为‎0.8m，则排水管内水的深度为 0.8 m． ‎ ‎16．若分式方程无解，则的值为 ．‎ ‎（第18题图）‎ ‎17．如图，一只蚂蚁沿着边长为2的正方体表面从点A出发，经过3个面爬到点B，如果它运动的路径是最短的，则AC的长为 ．‎ ‎（第17题图）‎ 第15题图 ‎18．如图放置的△OAB1，△B‎1A1B2，△B‎2A2B3，…都是边长为1的等边三角形，点A在 轴上，点O，B1，B2，B3，…都在直线上，则点A2015的坐标是 （，）． ．‎ 三、解答题：本大题共7小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ ‎19． (本题满分7分，第⑴题3分，第⑵题4分) ‎ ‎（1）计算：‎ 解： ‎ ‎=………………………………………2分 ‎=…………………………………………………………………3分 ‎（2）解方程组： ‎ 解：①+②得：3x=15………………③‎ ‎∴x=5…………………………………………………………2分 将x=5代人①，得：‎ ‎∴y=1………………………………………………3分 ‎∴方程组的解为……………………………4分 ‎20．(本题满分8分) 东营市为进一步加强和改进学校体育工作，切实提高学生体质健康水平，决定推进“一校一球队、一级一专项、一人一技能”活动计划．某校决定对学生感兴趣的球类项目（A：足球， B：篮球， C：排球，D：羽毛球，E：乒乓球）进行问卷调查，学生可根据自己的喜好选修一门，李老师对某班全班同学的选课情况进行统计后，制成了两幅不完整的统计图（如图）．‎ ‎（1）将统计图补充完整；‎ ‎（2）求出该班学生人数；‎ ‎（3）若该校共有学生3500名，请估计有多少人选修足球？‎ ‎（4）该班班委5人中，1人选修篮球，3人选修足球，1人选修排球，李老师要从这5人中任选2人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．‎ ‎（第20题图）‎ ‎（1）如图……………………………………………………………………2分 ‎（2）该班人数：（人）……………………………………3分 ‎（3）选修足球的人数：（人）………………………4分 第一人 ‎（4）用“‎1”‎代表篮球，“2、3、‎4”‎代表足球，“‎5”‎代表排球，可以用下表列举出所有可能出现的结果．‎ 第二人 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎1‎ ‎（2,1）‎ ‎（3,1）‎ ‎（4,1）‎ ‎（5,1）‎ ‎2‎ ‎（1，2）‎ ‎（3,2）‎ ‎（4,2）‎ ‎（5,2）‎ ‎3‎ ‎（1,3）‎ ‎（2,3）‎ ‎（4,3）‎ ‎（5,3）‎ ‎4‎ ‎（1,4）‎ ‎（2,4）‎ ‎（3,4）‎ ‎（5,4）‎ ‎5‎ ‎（1,5）‎ ‎（2,5）‎ ‎（3,5）‎ ‎（4,5）‎ ‎…………………………………………………………………………………6分 由图可以看出，可能出现的结果有20种，并且它们出现的可能性相等．选出的两人1人选修篮球，1人选修足球（记为事件A）的结果有6种，即（1，2），（1，3），（1，4），（2，1），（3，1），（4，1），所以P(A)= …………………………………8分 ‎21．(本题满分8分)已知在△ABC中，∠B=90o，以AB上的一点O为圆心，以OA为半径的圆交AC于点D，交AB于点E．‎ ‎（1）求证：AC·AD=AB·AE；‎ ‎（2）如果BD是‎（第21题图）‎ ⊙O的切线，D是切点，E是OB的中点，当BC=2时，求AC的长．‎ ‎（1）证明：连接DE ‎∵AE是直径 ‎∴∠ADE=90o ‎∴∠ADE=∠ABC 在Rt△ADE和Rt△ABC中，∠A是公共角 故△ADE∽△ABC………………………………2分 则，即AC·AD=AB·AE…………4分 ‎（2）解：连接OD ‎∵BD是圆O的切线 则OD⊥BD……………………………………………………………………5分 在Rt△OBD中，OE=BE=OD ‎∴OB=2OD ‎∴∠OBD=30o…………………………………………………………………6分 同理∠BAC=30o………………………………………………………………7分 在Rt△ABC中AC=2BC=2×2=4……………………………………………8分 ‎22．(本题满分8分)如图是函数与函数在第一象限内的图象，点是的图象上一动点，轴于点A，交的图象于点，轴于点B，交的图象于点．‎ ‎（第22题图）‎ ‎（1）求证：D是BP的中点；‎ ‎（2）求出四边形ODPC的面积．‎ ‎ ‎ ‎（第22题图）‎ ‎（1）证明：‎ ‎∵点P在函数上 ‎∴设P点坐标为（，m）……………1分 ‎∵点D在函数上，BP∥轴 ‎∴设D点坐标为（，m）……………2分 由题意可得 BD=，BP=‎ 故D是BP的中点……………………………………………………………4分 ‎（2）解：S四边形PBOA =﹒m=6………………………………………………5分 设C点坐标为（，） D点坐标为（，）‎ 则S△OBD==………………………………………………………6分 S△OAC==…………………………………………………………7分 ‎∴S四边形ODPC=S四边形PBOA—S△OBD—S△OAC=6——=3……………………8分 ‎23．(本题满分8分)2013年，东营市某楼盘以每平方米6500元的均价对外销售．因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．‎ ‎（1）求平均每年下调的百分率；‎ ‎（2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套‎100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）‎ 解：（1）设平均每年下调的百分率为，根据题意，得：‎ ‎………………………………………………………3分 解得： =0.1=10%， =1.9（不合题意，舍去）…………………………4分 答：平均每年下调的百分率为10%．…………………………………………5分 ‎（2）如果下调的百分率相同，2016年的房价为：‎ ‎5265×（1-10%）=4738.5（元/）………………………………………6分 则‎100平方米的住房的总房款为 ‎100×4738.5=473850（元）=47.385（万元）……………………………7分 ‎∵20+30＞47.385‎ ‎∴张强的愿望可以实现. ……………………………………………………8分 ‎24．(本题满分10分)如图，两个全等的△和△重叠在一起，固定△，将△进行如下变换：‎ ‎（1）如图1，△沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD，请直接写出与的关系；‎ ‎（2）如图2，当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△应满足什么条件？请给出证明；‎ ‎（3）在（2）的条件下，将△沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请你在图3的位置画出图形，并求出的值． ‎ ‎（第24题图1）‎ ‎（第24题图2）‎ ‎（第24题图3）‎ 解：(1) =……………………………………………………1分 ‎(2) △为等腰直角三角形，即：………………2分 ‎（第24题图2）‎ 理由如下：‎ ‎∵Ｆ为BC的中点 ‎∴CF=BF ‎∵CF= AD ‎∴AD= BF 又∵AD∥BF ‎∴四边形AFBD为平行四边形……………………………………………………………3分 ‎∵AB=AC,Ｆ为BC的中点 ‎∴AF⊥BC ‎∴平行四边形AFBD为矩形………………………………………………………………4分 ‎∵,F为BC的中点 ‎∴AF=BC=BF ‎∴四边形AFBD为正方形…………………………………………………………………5分 ‎(3)正确画出图形……………………………………………………………………………6分 ‎（第25题）图3‎ 由（2）知，△为等腰直角三角形, AF⊥BC 设CF=,则GF=EF=CB=2．‎ 由勾股定理，得：………………………8分 ‎=………………………10分 ‎25．(本题满分13分)如图，抛物线经过A（），B（），C（）三点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在直线AC下方的抛物线上有一点D，使得△DCA的面积最大，求点D的坐标；‎ ‎（3）设点M是抛物线的顶点，试判断抛物线上是否存在点H满足？若存在，请求出点H的坐标；若不存在，请说明理由．‎ ‎（第25题图）‎ 解：（1）∵该抛物线过点C（0，2），‎ ‎∴可设该抛物线的解析式为．‎ 将A（-2，0），B（-，0）代入，得，‎ 解得：‎ ‎∴此抛物线的解析式为；……………………………………………4分 ‎（2）由题意可求得直线AC的解析式为．………………………………………5分 如图，设D点的横坐标为t（-2＜t＜0），则D点的纵坐标为．‎ 过D作y轴的平行线交AC于E．‎ ‎∴E点的坐标为．‎ ‎∴，用h表示点C到线段DE所在直线的距离，‎ ‎∴‎ ‎………………………………………………7分 ‎∵-2＜t＜0‎ ‎∴当t=-1时，△DAC面积最大，此时点D的坐标为（-1，-1）．…………………8分 ‎（3）点H存在．………………………………………………………………………9分 由（1）知，点M的坐标为 解法一：如图，假设存在点H，满足 作直线MH交轴于点K(，0)，作MN⊥轴于点N． ‎ ‎∵,‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴点K的坐标为（）……………………………………………………………11分 所以直线MK的解析式为.‎ ‎∴ 把①代入②，化简，得：．‎ ‎＞0． …………………………………12分 ‎∴，．将代入中，解得 ‎∴ 直线MN与抛物线有两个交点（其中一点为顶点M）．‎ ‎∴ 抛物线上必存在一点H，使∠AMH＝90˚， ‎ 此时点H坐标为．…………………………………………………13分 解法二：如图，过点A作直线,过顶点M作MN⊥AM，MF分别交直线于点N和点F．则 ∠FMN＋∠AMF＝90˚． ‎ ‎∵ ∠MAF＋∠AMF＝90˚， ‎ ‎∴ ∠MAF＝∠FMN． ‎ 又∵ ∠AFM＝∠MFN＝90˚， ‎ ‎∴ △AFM∽△MFN． ‎ ‎∴ AF∶MF＝MF∶FN． 即 ‎ ‎∴ FN＝． ‎ ‎∴ 点N的坐标为． …………………11分 设过点M，N的直线的解析式为．‎ 将M,N代入得：‎ ‎ 解得：‎ 所以直线MN的解析式为 ‎∴ 把①代入②，化简，得：．‎ ‎＞0．…………………………………12分 ‎ ∴，．将代入中，解得 ‎∴ 直线MN与抛物线有两个交点（其中一点为顶点M）．‎ ‎∴ 抛物线上必存在一点H，使∠AMH＝90˚， ‎ 此时点H坐标为．…………………………………………………13分