- 2021-05-22 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
沪科版八年级数学上册期末测试题1(含答案)
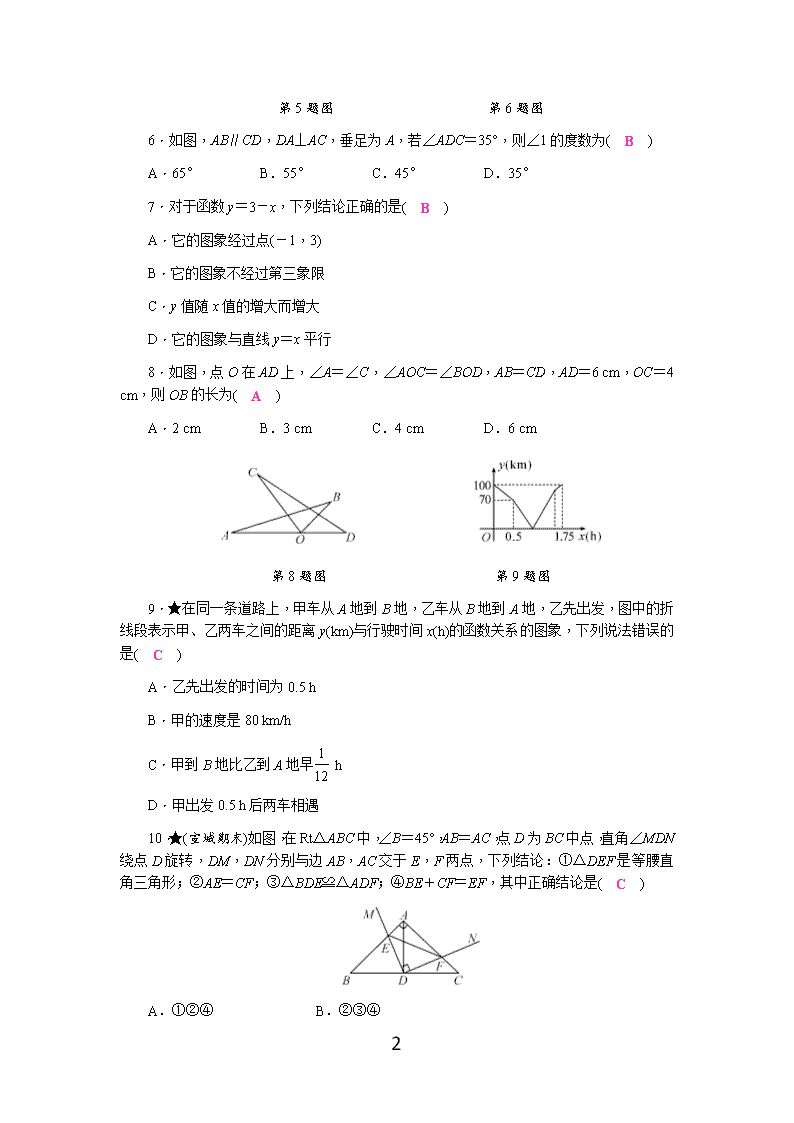
沪科版八年级数学上册期末测试题1(含答案) (考试时间:120分钟 满分:150分) 分数:__________ 一、选择题(本大题共10小题,每小题4分,满分40分) 每小题都给出A、B、C、D四个选项,其中只有一个是正确的. 1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( A ) A B C D 2.已知三角形的两边长分别为4 cm和10 cm,则第三边长可以是( A ) A.13 cm B.16 cm C.6 cm D.5 cm 3.下列命题中,是假命题的是( B ) A.对顶角相等 B.同旁内角互补 C.两点确定一条直线 D.角平分线上的点到这个角的两边的距离相等 4.在平面直角坐标系中,点A(m,3)与点B(2,n)关于y轴对称,则( A ) A.m=-2,n=3 B.m=2,n=-3 C.m=3,n=-2 D.m=-3,n=2 5.如图所示,点A,点B所在的位置分别是( D ) A.第二象限,y轴上 B.第四象限,y轴上 C.第二象限,x轴上 D.第四象限,x轴上 10 第5题图 第6题图 6.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( B ) A.65° B.55° C.45° D.35° 7.对于函数y=3-x,下列结论正确的是( B ) A.它的图象经过点(-1,3) B.它的图象不经过第三象限 C.y值随x值的增大而增大 D.它的图象与直线y=x平行 8.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=6 cm,OC=4 cm,则OB的长为( A ) A.2 cm B.3 cm C.4 cm D.6 cm 第8题图 第9题图 9.★在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(km)与行驶时间x(h)的函数关系的图象,下列说法错误的是( C ) A.乙先出发的时间为0.5 h B.甲的速度是80 km/h C.甲到B地比乙到A地早 h D.甲出发0.5 h后两车相遇 10.★(宣城期末)如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( C ) A.①②④ B.②③④ 10 C.①②③ D.①②③④ 二、填空题(本大题共4小题,每小题5分,满分20分) 11.函数y=|x|-1中的自变量x的取值范围是 x为全体实数 . 12.(安徽中考)命题“如果a+b=0,那么a,b互为相反数”的逆命题为 如果a,b互为相反数,那么a+b=0 . 13.如图,已知一次函数y=kx+b和y=mx+n的图象交于点P,则根据图象可得不等式组0<mx+n<kx+b的解集是 -3<x<-1 . 14.★(临泉县期末)在平面直角坐标系中,若点A(0,4),B(3,0),AB=5.请在x轴上找一点C,使△ABC是以AB为腰的等腰三角形,点C的坐标为 (-3,0)或(-2,0)或(8,0) . 选择、填空题答题卡 一、选择题(每小题4分,共40分) 题号 1 2 3 4 5 得分 答案 A A B A D 题号 6 7 8 9 10 答案 B B A C C 二、填空题(每小题5分,共20分)得分:______ 11. x为全体实数 12.__如果a,b互为相反数,那么a+b=0__ 13. -3<x<-1 14.__(-3,0)或(-2,0)或(8,0)__ 三、(本大题共2小题,每小题8分,满分16分) 15.如图,△ABC中,∠B=45°,∠C=38°,E是BC边上一点,ED交CA的延长线于点D,交AB于点F,∠D=32°.求∠AFE的大小. 10 解:∵∠B=45°,∠C=38°, ∴∠DAB=45°+38°=83°, ∵∠D=32°, ∴∠AFE=83°+32°=115°. 16.如图,三角形AOB中,A,B两点的坐标分别为(-4,-6),(-6,-3),求三角形AOB的面积(提示:三角形AOB的面积可以看作一个梯形的面积减去一些小三角形的面积). 解:S△AOB=S梯形BCDO-(S△ABC+S△OAD) =×(3+6)×6- =27-(3+12) =12. 四、(本大题共2小题,每小题8分,满分16分) 17.(瑶海区期末)(1)如图①,已知△DEF,用直尺和圆规在△DEF内作出点P,使点P到△DEF三边距离相等(不写作法,保留作图痕迹); (2)如图②,在图示的网格中,作出△ABC关于MN对称的图形△A1B1C1;说明△A2B2C2是由△A1B1C1经过怎样的平移得到的? 10 解:(1)如图①所示, 点P即为所求作的点. (2)如图②所示, △A1B1C1即为所求作的图形; △A2B2C2是由△A1B1C1经过向右平移6个单位、再向下平移2个单位得到的. 18.如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为点E.若BC=3. (1)求∠B的度数; (2)求DE的长. 解:(1)∵DE垂直平分AB, ∴DA=DB, ∴∠B=∠DAB. ∵AD平分∠CAB, ∴∠CAD=∠DAB. ∵∠C=90°, ∴3∠CAD=90°, ∴∠CAD=30°, ∴∠B=30°. (2)∵AD平分∠CAB,DE⊥AB,CD⊥AC, 10 ∴CD=DE=BD. ∵BC=3, ∴DE=CD=1. 五、(本大题共2小题,每小题10分,满分20分) 19.如图,正比例函数y=2x的图象与一次函数y=kx+b(k≠0)的图象交于点A(m,2),一次函数y=kx+b(k≠0)的图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D. (1)求一次函数表达式; 解:∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2), ∴2m=2, 解得m=1, ∴A(1,2), 把A(1,2)和B(-2,-1)代入y=kx+b(k≠0), 得 解得k=1,b=1, 则一次函数表达式是y=x+1. (2)求△AOD的面积. 解:y=x+1中,令y=0,则x=-1, ∴D(-1,0), ∴△AOD的面积=×1×2=1. 10 20.(蜀山区期末)如图①,在边长均为1个单位的小正方形组成的4×3的网格中,给出了以格点(网格线的交点)为顶点的格点△ABC,请在图②-④中各画出一个与图①中△ABC全等但在网格中位置不同的格点三角形. 解:如图所示. 六、(本题满分12分) 21.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: (1)△AEF≌△CEB; (2)AF=2CD. 证明:(1)∵AD⊥BC,CE⊥AB, ∴∠BCE+∠CFD=90°,∠BCE+∠B=90°, ∴∠CFD=∠B. ∵∠CFD=∠AFE, ∴∠AFE=∠B. 在△AEF与△CEB中, ∴△AEF≌△CEB.(AAS) (2)∵AB=AC,AD⊥BC, ∴BC=2CD. ∵△AEF≌△CEB, 10 ∴AF=BC, ∴AF=2CD. 七、(本题满分12分) 22.甲、乙两人驾车都从P地出发,沿一条笔直的公路匀速前往Q地,乙先出发一段时间后甲再出发,甲,乙两人到达Q地后均停止.已知P,Q两地相距200 km,设乙行驶的时间为t(h),甲、乙两人之间的距离为y(km),表示y与t函数关系的部分图象如图所示.请解决以下问题: (1)由图象可知,甲比乙迟出发 1 h,图中线段BC所在直线的函数表达式为 y=15x-40 ; (2)设甲的速度为v1 km/h,求出v1的值; (3)根据题目信息补全函数图象(不需要写出分析过程,但必须标明关键点的坐标);并直接写出当甲,乙两人相距32 km时t的值. 解:(1)设线段BC所在直线的函数表达式为y=kx+b,根据题意得: 解得 ∴线段BC所在直线的表达式为 y=15x-40. 故答案为1;y=15x-40. (2)设甲的速度为v1 km/h,设乙的速度为v2 km/h,由题意得 解得 答:甲的速度为v1=40 km/h. (3)如图所示. 10 根据题意得 40(t-1)-25t=32或25t=200-32, 解得t=4.8或6.72. 答:当甲、乙两人相距32 km时t的值为4.8或6.72. 八、(本题满分14分) 23.(安庆期末)(1)模型建立: 如图①,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA; (2)模型应用: ①如图②,一次函数y=-2x+4的图象分别与x轴,y轴交于点A,B,以线段AB为腰在第一象限内作等腰直角三角形ABC,则C点的坐标为__(4,6)或(6,2)__(直接写出结果); ②如图③,在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=45°,连接BD,AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点. (1)证明:∵AD⊥ED,BE⊥ED, ∴∠D=∠E=90°,∴∠ACD+∠CAD=90°. ∵∠ACB=90°,∴∠ACD+∠BCE=90°, ∴∠BCE=∠CAD. 在△BEC和△CDA中, ∴△BEC≌△CDA.(AAS) (2)①解:如图②,过点C作CH⊥x轴于点H, 同(1)的方法得,△ACH≌△BAO,(AAS) ∴AH=OB=4,CH=OA=2, 10 ∴OH=OA+AH=6, ∴C(6,2), 过点C′作C′H′⊥y轴于点H′, 同理:C′(4,6).故答案为:(4,6)或(6,2); ②证明:如图③,作BP⊥MN交MN的延长线于点P,作DQ⊥MN于点Q. ∵CA=CB,∠CAB=45°, ∴∠CBA=∠CAB=45°,∴∠ACB=90°. ∵CM⊥AE,∴∠AMC=90°=∠ACB. ∵∠BCP+∠BCA=∠CAM+∠AMC, ∵∠BCA=∠AMC,∴∠BCP=∠CAM, 在△CBP与△ACM中, ∴△CBP≌△ACM,(AAS) ∴MC=BP, 同理,CM=DQ,∴DQ=BP. 在△BPN与△DQN中, ∴△BPN≌△DQN,(AAS) ∴BN=ND,∴N是BD的中点. 10查看更多