【数学】2019届高考一轮复习北师大版理4-7正弦定理与余弦定理学案
第7讲 正弦定理与余弦定理
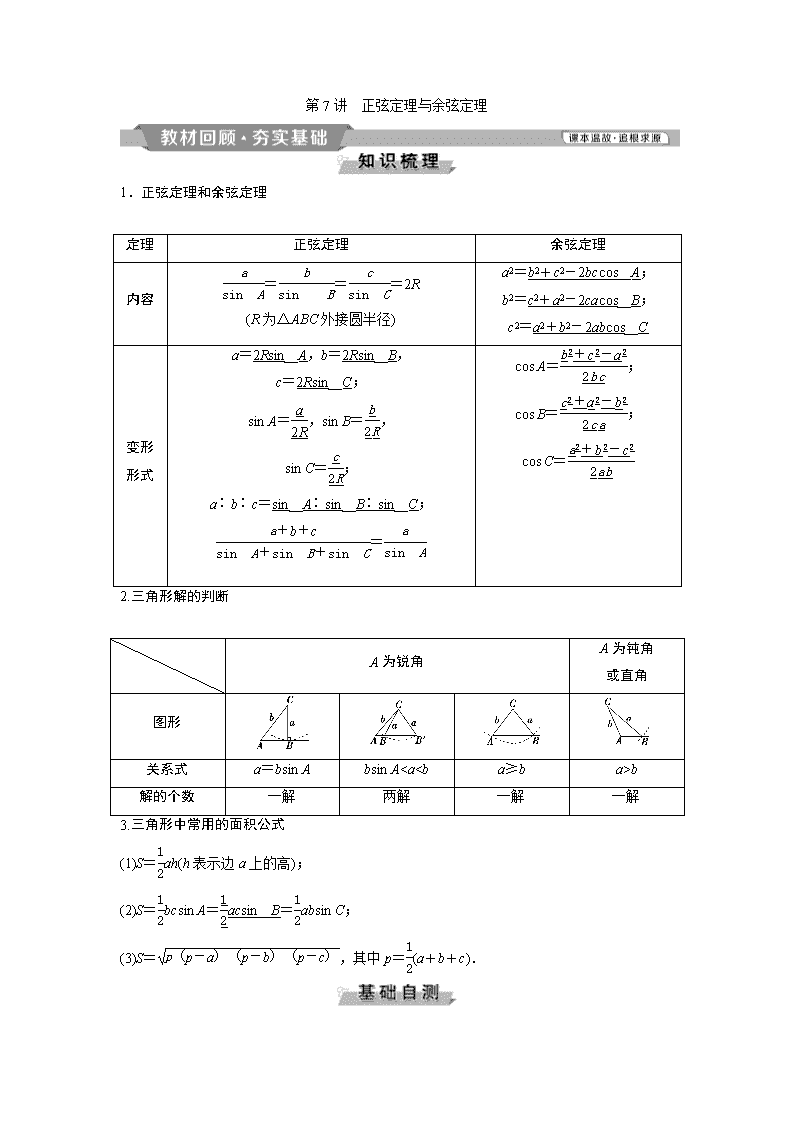
1.正弦定理和余弦定理
定理
正弦定理
余弦定理
内容
===2R
(R为△ABC外接圆半径)
a2=b2+c2-2bccos__A;
b2=c2+a2-2cacos__B;
c2=a2+b2-2abcos__C
变形形式
a=2Rsin__A,b=2Rsin__B,
c=2Rsin__C;
sin A=,sin B=,
sin C=;
a∶b∶c=sin__A∶sin__B∶sin__C;
=
cos A=;
cos B=;
cos C=
2.三角形解的判断
A为锐角
A为钝角
或直角
图形
关系式
a=bsin A
bsin A
b
解的个数
一解
两解
一解
一解
3.三角形中常用的面积公式
(1)S=ah(h表示边a上的高);
(2)S=bcsin A=acsin__B=absin C;
(3)S=,其中p=(a+b+c).
判断正误(正确的打“√”,错误的打“×”)
(1)在△ABC中,已知a,b和角B,能用正弦定理求角A;已知a,b和角C,能用余弦定理求边c.( )
(2)在三角形中,已知两角和一边或已知两边和一角都能解三角形.( )
(3)在△ABC中,sin A>sin B的充分不必要条件是A>B.( )
(4)在△ABC中,a2+b20,cos B=.又00,则cos B=,故a=5.
(2)由(1)知,sin B=,由S=acsin B=9,得c=6.
由b2=a2+c2-2accos B=13,得b=.
故△ABC的周长为11+.
1.(2018·长沙市统一模拟考试)△ABC中,C=,AB=3,则△ABC的周长为( )
A.6sin+3 B.6sin+3
C.2sin+3 D.2sin+3
解析:选C.设△ABC的外接圆半径为R,则2R==2,于是BC=2Rsin A=2sin A,AC=2Rsin B=2sin,于是△ABC的周长为2[sin A+sin]+3=2sin+3.选C.
2.(2018·安徽江南十校联考)设△ABC的面积为S1,它的外接圆面积为S2,若△ABC的三个内角大小满足A∶B∶C=3∶4∶5,则的值为( )
A. B.
C. D.
解析:选D.在△ABC中,A+B+C=π,
又A∶B∶C=3∶4∶5,所以A=,B=,C=π.
由正弦定理===2R(a、b、c为△ABC中角A、B、C的对边,R为△ABC的外接圆半径)可得,a=·c,b=·c,R=.
所以S1=absin C=···c2·sin C
=sin A·sin B·sin C·,
S2=πR2=·,
所以===,故选D.
3.如图,在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,则BC的长为________.
解析:在△ABD中,设BD=x,则
BA2=BD2+AD2-2BD·AD·cos∠BDA,
即142=x2+102-2·10x·cos 60°,
整理得x2-10x-96=0,
解得x1=16,x2=-6(舍去).
在△BCD中,由正弦定理:=,所以BC=·sin 30°=8.
答案:8
4.在△ABC中,角A、B、C的对边分别是a、b、c,=a,a=2.若b∈[1,3],则c的最小值为________.
解析:由=a,得=sin C.由余弦定理可知cos C=
,即3cos C=sin C,所以tan C=,故cos C=,所以c2=b2-2b+12=(b-)2+9,因为b∈[1,3],所以当b=时,c取最小值3.
答案:3
5.(2018·洛阳市第一次统一考试)如图,平面四边形ABDC中,∠CAD=∠BAD=30°.
(1)若∠ABC=75°,AB=10,且AC∥BD,求CD的长;
(2)若BC=10,求AC+AB的取值范围.
解:(1)由已知,易得∠ACB=45°,
在△ABC中,=⇒BC=5.
因为AC∥BD,所以∠ADB=∠CAD=30°,∠CBD=∠ACB=45°,
在△ABD中,∠ADB=30°=∠BAD,所以DB=AB=10.
在△BCD中,CD==5.
(2)AC+AB>BC=10,
cos 60°=⇒(AB+AC)2-100=3AB·AC,
而AB·AC≤,
所以≤,
解得AB+AC≤20,
故AB+AC的取值范围为(10,20].
6.已知a,b,c分别是△ABC中角A,B,C的对边,acsin A+4sin C=4csin A.
(1)求a的值;
(2)圆O为△ABC的外接圆(O在△ABC内部),△OBC的面积为,b+c=4,判断△ABC的形状,并说明理由.
解:(1)由正弦定理可知,sin A=,sin C=,
则acsin A+4sin C=4csin A⇔a2c+4c=4ac,
因为c≠0,所以a2c+4c=4ca⇔a2+4=4a⇔(a-2)2=0,可得a=2.
(2)设BC的中点为D,则OD⊥BC,
所以S△OBC=BC·OD.
又因为S△OBC=,BC=2,
所以OD=,
在Rt△BOD中,tan∠BOD====,
又0°<∠BOD<180°,所以∠BOD=60°,
所以∠BOC=2∠BOD=120°,
因为O在△ABC内部,
所以∠A=∠BOC=60°,
由余弦定理得a2=b2+c2-2bccos A.
所以4=b2+c2-bc=(b+c)2-3bc,又b+c=4,
所以bc=4,所以b=c=2,
所以△ABC为等边三角形.