苏教版数学八年级上册教案3-1勾股定理（2）

苏教版数学八年级上册教案3-1勾股定理（2）

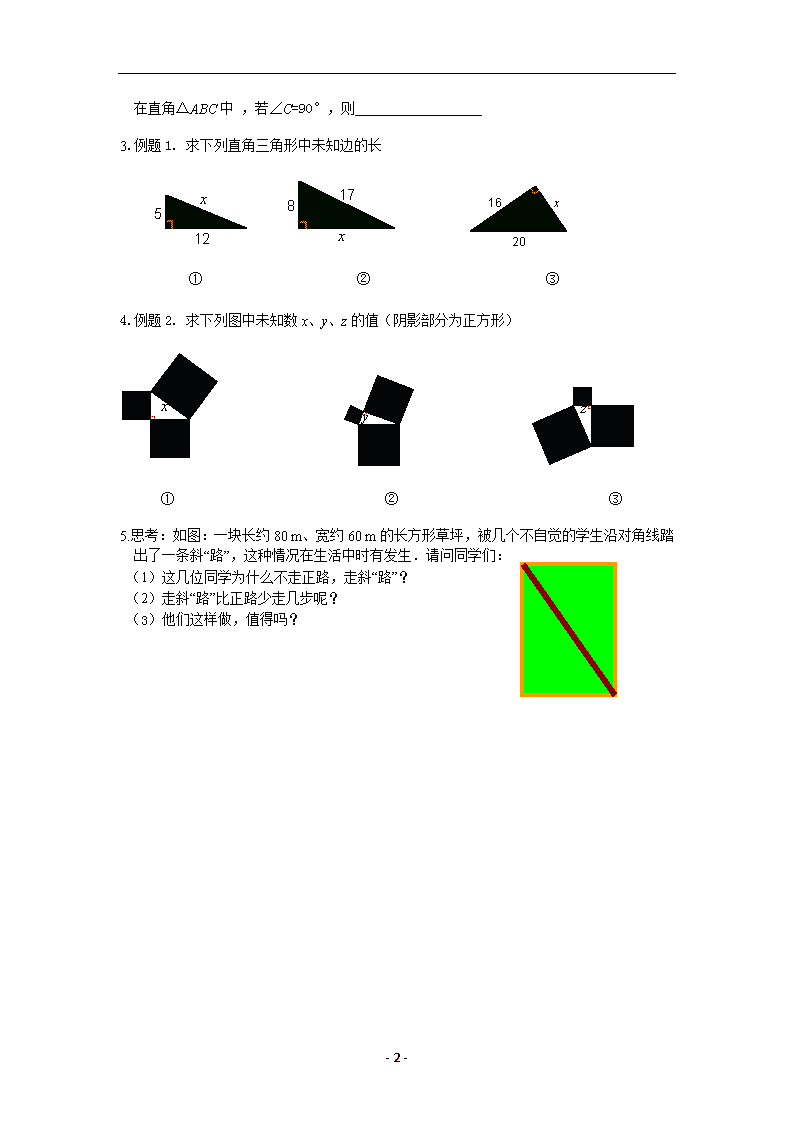
- 1 - 3.1 勾股定理（2） 教学目标 【知识与能力】 能说出勾股定理，并能用勾股定理解决简单问题 【过程与方法】 1.让学生经历从数到形再由形到数的转化过程，经历探求三个正方形面积间的关系转化为三 边数量关系的过程．并从过程中让学生体会数形结 合思想，发展将未知转化为已知，由特 殊推测一般的合情推理能力 2.经历探索勾股定理的过程，发展合情推理的能力，体会数形结合思想。 【情感态度价值观】 经历用多种拼图方法验证勾股定理的过程，发展用数学的眼光观察现实世界和有条理地思考 与表达的能力，感受勾股定理的文化价值 教学重难点 【教学重点】 勾股定理的探索过程．通过综合运用已有知识解决问题的过程，加深对数形结合的思想认识 [ 【教学难点】 通过拼图验证勾股定理的过程，使学生获得一些研究问题与合作交流的方法与经验[ 课前准备 无 教学过程 一、预习·质疑 1．同学们，我们已经学过三角形的一些基本知识，如果一个三角形的两条边分别长 6 和 8， 你知道第三边的长吗？你知道第三边长的范围吗？ 2．如果又已知这两边的夹角是 90 度，那么第三边的长确定吗？ 二、展示·探究 1. 如图，把火柴盒放倒，在这个过程中，我们可以探索得出 cba 、、 之间的数量关系 a b b c c A D EC B 2.通过以上计算我们可以发现： 问题 1：△ABD 是什么三角形 问题 2：你有几种方法求梯形 ACED 的面积？（用含有 a、b、c 的代数式表示） - 2 - 在直角△ABC 中 ，若∠C=90°，则 3.例题 1. 求下列直角三角形中未知边的长 ① ② ③ 4.例题 2. 求下列图中未知数 x、y、z 的值（阴影部分为正方形） ① ② ③] 5.思考：如图：一块长约 80 m、宽约 60 m 的长方形草坪，被几个不自觉的学生沿对角线踏 出了一条斜“路”，这种情况在生活中时有发生．请问同学们： （1）这几位同学为什么不走正路，走斜“路”？ （2）走斜“路”比正路少走几步呢？ （3）他们这样做，值得吗？