【数学】2018届一轮复习北师大版第八章解析几何第五节椭圆教案
第五节 椭圆
☆☆☆2017考纲考题考情☆☆☆
考纲要求
真题举例
命题角度
1.掌握椭圆的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率);
2.了解椭圆的简单应用;
3.理解数形结合的思想。
2016,全国卷Ⅲ,11,5分(椭圆的几何性质)
2016,天津卷,19,14分(椭圆的标准方程、直线与椭圆的位置关系)
2016,浙江卷,9,5分(椭圆的几何性质)
2016,江苏卷,10,5分(椭圆的几何性质)
2015,全国卷Ⅰ,14,5分(椭圆的几何性质)
椭圆的定义、标准方程、几何性质通常以小题形式考查,直线与椭圆的位置关系主要出现在解答题中。椭圆的考查频率非常高,而且运算量、思维量都比较大,这是椭圆命题的一个显著特征。
微知识 小题练
自|主|排|查
1.椭圆的概念
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
集合P={M||MF1|+|MF2|=2a,|F1F2|=2c,其中a>0,c>0,且a,c为常数}。
(1)若a>c,则集合P为椭圆;
(2)若a=c,则集合P为线段;
(3)若a<c,则集合P为空集。
2.椭圆的标准方程和几何性质
标准方程
+=1(a>b>0)
+=1(a>b>0)
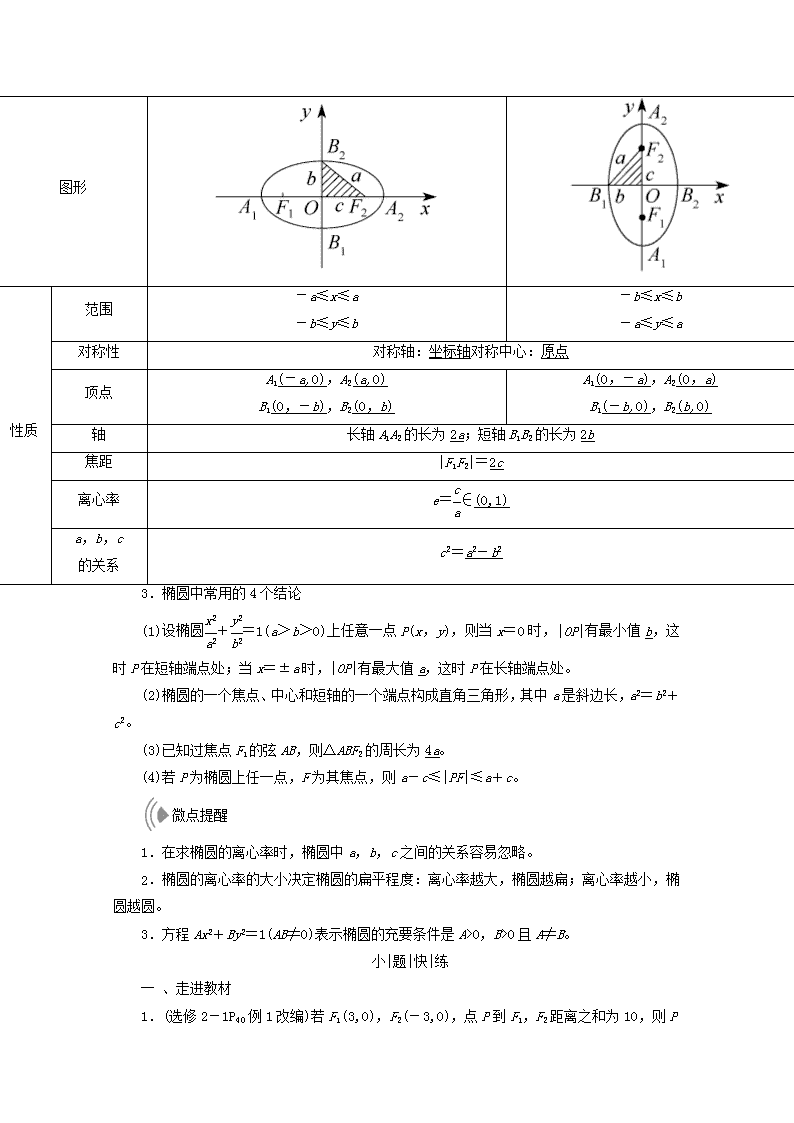
图形
性质
范围
-a≤x≤a
-b≤y≤b
-b≤x≤b
-a≤y≤a
对称性
对称轴:坐标轴对称中心:原点
顶点
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
轴
长轴A1A2的长为2a;短轴B1B2的长为2b
焦距
|F1F2|=2c
离心率
e=∈(0,1)
a,b,c
的关系
c2=a2-b2
3.椭圆中常用的4个结论
(1)设椭圆+=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时P在短轴端点处;当x=±a时,|OP|有最大值a,这时P在长轴端点处。
(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2。
(3)已知过焦点F1的弦AB,则△ABF2的周长为4a。
(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c。
微点提醒
1.在求椭圆的离心率时,椭圆中a,b,c之间的关系容易忽略。
2.椭圆的离心率的大小决定椭圆的扁平程度:离心率越大,椭圆越扁;离心率越小,椭圆越圆。
3.方程Ax2+By2=1(AB≠0)表示椭圆的充要条件是A>0,B>0且A≠B。
小|题|快|练
一 、走进教材
1.(选修2-1P40例1改编)若F1(3,0),F2(-3,0),点P到F1,F2距离之和为10,则P
点的轨迹方程是( )
A.+=1 B.+=1
C.+=1 D.+=1或+=1
【解析】 设点P的坐标为(x,y),因为|PF1|+|PF2|=10>|F1F2|=6,所以点P的轨迹是以F1,F2为焦点的椭圆,其中a=5,c=3,b==4,故点P的轨迹方程为+=1。故选A。
【答案】 A
2.(选修2-1P49A组T6改编)设椭圆的两个焦点分别为F1,F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( )
A. B.
C.2- D.-1
【解析】 解法一:设椭圆方程为+=1,依题意,显然有|PF2|=|F1F2|,则=2c,即=2c,即e2+2e-1=0,解得e=-1。故选D。
解法二:因为△F1PF2为等腰直角三角形,所以|PF2|=|F1F2|=2c,|PF1|=2c。因为|PF1|+|PF2|=2a,所以2c+2c=2a,所以e===-1。故选D。
【答案】 D
二、双基查验
1.设P是椭圆+=1上的点,若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于( )
A.4 B.8
C.6 D.18
【解析】 依定义知|PF1|+|PF2|=2a=6。故选C。
【答案】 C
2.方程+=1表示椭圆,则m的范围是( )
A.(-3,5) B.(-5,3)
C.(-3,1)∪(1,5) D.(-5,1)∪(1,3)
【解析】 由方程表示椭圆知
解得-3<m<5且m≠1。故选C。
【答案】 C
3.椭圆+=1的离心率为,则k的值为( )
A.-21 B.21
C.-或21 D.或21
【解析】 若a2=9,b2=4+k,则c=,
由=,即=,得k=-;
若a2=4+k,b2=9,则c=,
由=,即=,解得k=21。故选C。
【答案】 C
4.已知椭圆的一个焦点为F(1,0),离心率为,则椭圆的标准方程为________。
【解析】 设椭圆的标准方程为+=1(a>b>0),
因为椭圆的一个焦点为F(1,0),离心率e=,
所以解得
故椭圆的标准方程为+=1。
【答案】 +=1
5.已知F1,F2是椭圆C的左,右焦点,点P在椭圆上,且满足|PF1|=2|PF2|,∠PF1F2=30°,则椭圆的离心率为__________。
【解析】 在三角形PF1F2中,由正弦定理得
sin∠PF2F1=1,即∠PF2F1=,
设|PF2|=1,则|PF1|=2,|F2F1|=,
所以离心率e==。
【答案】
第一课时 椭圆的概念及其性质
微考点 大课堂
考点一
椭圆的定义及应用
【典例1】 (1)(2016·北京东城期末)过椭圆4x2+y2=1的一个焦点F1的直线与椭圆交于A,B两点,则A与B和椭圆的另一个焦点F2构成的△ABF2的周长为( )
A.2 B.4
C.8 D.2
(2)F1,F2是椭圆+=1的两个焦点,A为椭圆上一点,且∠AF1F2=45°,则△AF1F2的面积为( )
A.7 B.
C. D.
【解析】 (1)因为椭圆方程为4x2+y2=1,所以a=1。根据椭圆的定义,知△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=(|AF1|+|AF2|)+(|BF1|+|BF2|)=4a=4。故选B。
(2)由题意得a=3,b=,c=,∴|F1F2|=2,|AF1|+|AF2|=6。
∵|AF2|2=|AF1|2+|F1F2|2-2|AF1|·|F1F2|cos45°=|AF1|2-4|AF1|+8,∴(6-|AF1|)2=|AF1|2-4|AF1|+8。∴|AF1|=。
∴S=××2×=。故选C。
【答案】 (1)B (2)C
反思归纳 1.椭圆定义的应用范围
(1)确认平面内与两定点有关的轨迹是否为椭圆。
(2)解决与焦点有关的距离问题。
2.焦点三角形的应用
椭圆上一点P与椭圆的两焦点组成的三角形通常称为“焦点三角形”,利用定义可求其周长;利用定义和余弦定理可求|PF1||PF2|;通过整体代入可求其面积等。
【变式训练】 (1)已知A,B是圆2+y2=4(F为圆心)上一动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程为________。
(2)已知F是椭圆5x2+9y2=45的左焦点,P是此椭圆上的动点,A(1,1)是一定点。求|PA|+|PF|的最大值和最小值。
【解析】 (1)如图,由题意知|PA|=|PB|,|PF|+|BP|=2。所以|PA|+|PF|=2且|PA|+|PF|>|AF|,即动点P的轨迹是以A,F为焦点的椭圆,a
=1,c=,b2=。所以动点P的轨迹方程为x2+y2=1。
(2)如图所示,设椭圆右焦点为F1,则|PF|+|PF1|=6。
∴|PA|+|PF|=|PA|-|PF1|+6。
利用-|AF1|≤|PA|-|PF1|≤|AF1|(当P,A,F1共线时等号成立),
∴|PA|+|PF|≤6+,|PA|+|PF|≥6-。
故|PA|+|PF|的最大值为6+,最小值为6-。
【答案】 (1)x2+y2=1
(2)最大值6+,最小值6-
考点二
椭圆的标准方程及其应用
【典例2】 (1)若直线x-2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的标准方程为( )
A.+y2=1
B.+=1
C.+y2=1或+=1
D.以上答案都不对
(2)设F1,F2分别是椭圆E:x2+=1(0
0,B>0,A≠B)。
【变式训练】 (1)已知椭圆C:+=1(a>b>0)的左、右焦点为F1,F2,离心率为,过F2的直线l交C于A,B两点,若△AF1B的周长为4,则C的方程为( )
A.+=1 B.+y2=1
C.+=1 D.+=1
(2)过点(,-),且与椭圆+=1有相同焦点的椭圆的标准方程为_________________________________________________________。
【解析】 (1)因为△AF1B的周长为4,所以4a=4,所以a=,因为离心率为,所以c=1,所以b==,所以椭圆C的方程为+=1。故选A。
(2)椭圆+=1的焦点为(0,-4),(0,4),即c=4。由椭圆的定义知,2a=+,解得a=2。
由c2=a2-b2可得b2=4。所以所求椭圆的标准方程为+=1。
【答案】 (1)A (2)+=1
考点三
椭圆的简单几何性质……多维探究
角度一:与椭圆有关的最值或范围问题
【典例3】 已知点F1,F2是椭圆x2+2y2=2的左,右焦点,点P是该椭圆上的一个动点,那么|+|的最小值是( )
A.0 B.1
C.2 D.2
【解析】 设P(x0,y0),则=(-1-x0,-y0),
=(1-x0,-y0),∴+=(-2x0,-2y0),
∴|+|=
=2
=2。
∵点P在椭圆上,∴0≤y≤1,
∴当y=1时,|+|取最小值2。故选C。
【答案】 C
角度二:求离心率的值或范围
【典例4】 (1)(2016·全国卷Ⅲ)已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点。P为C上一点,且PF⊥x轴。过点A的直线l与线段PF交于点M,与y轴交于点E。若直线BM经过OE的中点,则C的离心率为( )
A. B.
C. D.
(2)(2015·福建高考)已知椭圆E:+=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点。若|AF|+|BF|=4,点M到直线l的距离不小于,则椭圆E的离心率的取值范围是( )
A. B.
C. D.
【解析】 (1)设E(0,m),则直线AE的方程为-+=1,由题意可知M,和B(a,0)三点共线,则=,化简得a=3c,则C的离心率e==。故选A。
(2)不妨设左焦点为F2,连接AF2,BF2,由椭圆的对称性可知四边形AFBF2的对角线互相平分,所以四边形AFBF2为平行四边形,所以|AF|+|BF|=|BF2|+|BF|=2a=4,所以a=2,设M(0,b),所以d=b≥⇒b≥1,所以e== ≤ =,又e∈
(0,1),所以e∈。故选A。
【答案】 (1)A (2)A
反思归纳 1.求椭圆离心率的方法
(1)直接求出a,c的值,利用离心率公式直接求解。
(2)列出含有a,b,c的齐次方程(或不等式),借助于b2=a2-c2消去b,转化为含有e的方程(或不等式)求解。
2.利用椭圆几何性质求值或范围的思路
求解与椭圆几何性质有关的参数问题时,要结合图形进行分析,当涉及顶点、焦点、长轴、短轴等椭圆的基本量时,要理清它们之间的关系。
微考场 新提升
1.曲线+=1与曲线+=1(k<9)的( )
A.长轴长相等 B.短轴长相等
C.离心率相等 D.焦距相等
解析 c2=25-k-(9-k)=16,所以c=4,所以两个曲线的焦距相等。故选D。
答案 D
2.椭圆+=1的左、右焦点分别为F1,F2,过F1作x轴的垂线交椭圆于A,B两点,则△ABF2的面积为( )
A. B.
C. D.21
解析 依题意得|AB|==,|F1F2|=2=6,因此△ABF2的面积等于|AB|×|F1F2|=××6=。故选A。
答案 A
3.(2016·全国卷Ⅰ)直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为( )
A. B.
C. D.
解析 通性通法:不妨设直线l过椭圆的上顶点(0,b)和左焦点(-c,0),b>0,c
>0,则直线l的方程为bx-cy+bc=0,由已知得=×2b,解得b2=3c2,又b2=a2-c2,所以=,即e2=,所以e=(e=-舍去)。故选B。
光速解法:不妨设直线l过椭圆的上顶点(0,b)和左焦点(-c,0),b>0,c>0,则直线l的方程为bx-cy+bc=0,由已知得=×2b,所以=×2b,所以e==。故选B。
答案 B
4.(2016·安徽皖西七校联考)已知圆M:(x+)2+y2=36,定点N(,0),点P为圆M上的动点,点Q在NP上,点G在线段MP上,且满足=2,·=0,则点G的轨迹方程是__________。
解析 由=2,·=0知,GQ是线段NP的垂直平分线,|GN|=|GP|,∴|GM|+|GN|=|MP|=6。点G的轨迹是以M,N为焦点的椭圆,由2a=6,得a=3。又c=,∴b2=4。点G的轨迹方程为+=1。
答案 +=1
5.设F1,F2为椭圆的两个焦点,以F2为圆心作圆,已知圆F2经过椭圆的中心,且与椭圆相交于点M,若直线MF1恰与圆F2相切,则该椭圆的离心率为________。
解析 由题意知∠F1MF2=,|MF2|=c,|F1M|=2a-c,则c2+(2a-c)2=4c2,e2+2e-2=0,解得e=-1。
答案 -1
第二课时 椭圆的综合问题
微考点 大课堂
考点一
直线与椭圆的相交弦长问题
【典例1】 椭圆两顶点A(-1,0),B(1,0),过焦点F(0,1)的直线l与椭圆交于C,D两点。当|CD|=时,求l的方程。
【解析】 由题意b=1,c=1。
∴a2=b2+c2=1+1=2。
∴椭圆方程为+x2=1。
若直线l斜率不存在时,|CD|=2,不合题意。
若直线l斜率存在时,设l方程y=kx+1,
联立得(k2+2)x2+2kx-1=0。
Δ=8(k2+1)>0恒成立。
设C(x1,y1),D(x2,y2)。
∴x1+x2=-,x1x2=-。
∴|CD|=|x1-x2|
=
=。
即=,
解得k2=2。∴k=±。
∴直线l方程为x-y+1=0或x+y-1=0。
【答案】 x-y+1=0或x+y-1=0
反思归纳 1.解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程(组),解决相关问题,涉及弦中点的问题常常用“点差法”解决,往往会更简单。
2.设直线与椭圆的交点坐标为A(x1,y1),B(x2,y2),
则|AB|=
=(k为直线斜率)。
【变式训练】 已知椭圆+=1(a>b>0)的一个顶点为B(0,4),离心率e=,直线l交椭圆于M,N两点。
(1)若直线l的方程为y=x-4,求弦MN的长;
(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l方程的一般式。
【解析】 (1)由已知得b=4,且=,即=。
∴=,解得a2=20。
∴椭圆方程为+=1。
则4x2+5y2=80与y=x-4联立。
消去y,得9x2-40x=0,∴x1=0,x2=。
∴所求弦长|MN|=|x2-x1|=。
(2)椭圆右焦点F的坐标为(2,0),设线段MN的中点为Q(x0,y0),由三角形重心的性质知=2。又B(0,4),∴(2,-4)=2(x0-2,y0)。故得x0=3,y0=-2,即得Q的坐标为(3,-2)。
设M(x1,y1),N(x2,y2),则x1+x2=6,y1+y2=-4,且+=1,+=1。
以上两式相减,得
+=0。
∴kMN==-·=-×=。
故直线MN的方程为y+2=(x-3),
即6x-5y-28=0。
【答案】 (1) (2)6x-5y-28=0
考点二
中点弦问题
【典例2】 已知椭圆+y2=1。
(1)求斜率为2的平行弦中点的轨迹方程;
(2)过N(1,2)的直线l与椭圆相交,求被l截得的弦的中点的轨迹方程;
(3)求过点P且被P点平分的弦所在直线的方程。
【解析】 设弦的两端点为A(x1,y1),B(x2,y2),中点为M(x0,y0),则有+y=1,+y=1。
两式作差,得+(y2-y1)(y2+y1)=0。
∵x1+x2=2x0,y1+y2=2y0,=kAB,
代入后求得kAB=-。①
(1)设弦中点为M(x,y),由①式,2=-,∴x+4y=0。又点M(x,y)在椭圆内部。
故所求的轨迹方程为x+4y=0。
(2)不妨设l交椭圆于A,B,弦中点为M(x,y),
由①式kl=kAB=-。
又∵kl=kMN=,∴-=。
整理,得x2+2y2-x-4y=00)的直线交E于A,M两点,点N在E上,MA⊥NA。
(1)当t=4,|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,求k的取值范围。
【解析】 (1)当t=4时,椭圆E的方程为+=1,A点坐标为(-2,0),设直线AM的方程为y=k(x+2)。由|AM|=|AN|可得M,N关于x轴对称,由MA⊥NA,可得直线AM的斜率为1,直线AM方程为y=x+2,代入椭圆+=1得7x2+16x+4=0,解得x=-2或-,M,N。于是△AMN的面积为××=。
(2)由题意知A(-,0)。设直线AM的方程为y=k(x+),
由得(3+tk2)x2+2tk2x+t2k2-3t=0,解得x=-或x=-,
所以|AM|==·。
同理可得|AN|=·。因为2|AM|=|AN|,所以2··=·
,整理得t=。
因为椭圆E的焦点在x轴上,所以t>3,即>3,整理得<0,
解得3。
【变式训练】 已知椭圆+=1(a>b>0)的左,右焦点分别为F1,F2,且|F1F2|=6,直线y=kx与椭圆交于A,B两点。
(1)若△AF1F2的周长为16,求椭圆的标准方程;
(2)①若k=,且A,B,F1,F2四点共圆,求椭圆离心率e的值;
②在①的条件下,设P(x0,y0)为椭圆上一点,若直线PA的斜率k1∈(-2,-1),试求直线PB的斜率k2的取值范围。
【解析】 (1)|F1F2|=6,即2c=6,c=3,又|AF1|+|AF2|=2a,而|AF1|+|AF2|+|F1F2|=16,所以2a=10,a=5,b=4,故椭圆的标准方程为+=1。
(2)①若A,B,F1,F2四点共圆,则AB,F1F2互相平分,必定有AF2⊥BF2。
将y=x与+=1联立整理,可得(a2+8b2)x2-8a2b2=0,设A(x1,y1),B(-x1,-y1),则x=,=(x1-c,y1),=(-x1-c,-y1),·=c2-x-y=c2-x=c2-=0,即a2c2+8b2c2=9a2b2,而b2=a2-c2,8e4-18e2+9=0,解得e2=(舍去),或e2=,因此e=。
②由e=和c=3,可得a=2,b=,椭圆的方程为+=1。
由A(x1,y1),B(-x1,-y1),k1=,k2=,
所以k1k2=。
又y=3,y=3,
所以=-,
即k1k2=-,k2=-。
由-2b>0)的离心率为e=,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)在( )
A.圆x2+y2=2内
B.圆x2+y2=2上
C.圆x2+y2=2外
D.以上三种情形都有可能
解析 由已知得e==,c=,x1+x2=-,x1x2=-,x+x=(x1+x2)2-2x1x2=+==<=2,因此点P(x1,x2)必在圆x2+y2=2内。故选A。
答案 A
3.直线m与椭圆+y2=1交于P1,P2两点,线段P1P2的中点为P,设直线m的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2的值为________。
解析 由点差法可求出k1=-·,
所以k1·=-,即k1k2=-。
答案 -
4.(2016·天津七校联考)设椭圆C:+=1(a>b>0)过点(0,4),离心率为。
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为的直线被C所截线段的中点坐标。
解析 (1)将点(0,4)代入C的方程得=1,
所以b=4。
又e==,得=,即1-=,
所以a=5。
所以椭圆C的方程为+=1。
(2)过点(3,0)且斜率为的直线方程为y=(x-3),
设直线与C的交点为A(x1,y1),B(x2,y2),
由消去y,得+=1,
即x2-3x-8=0。
所以AB的中点坐标x0==,y0=(x0-3)=-,
即所截线段的中点坐标为。
答案 (1)+=1 (2)