高考数学全国卷2理数

高考数学全国卷2理数

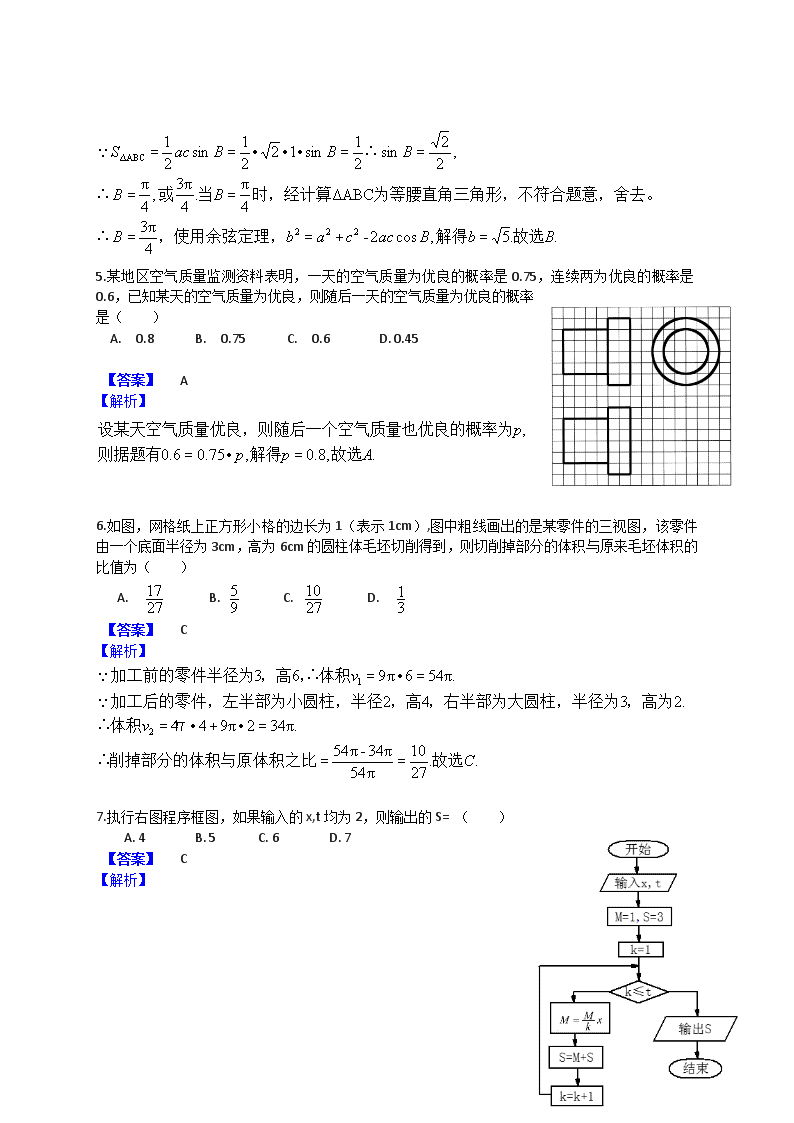
绝密★启用前 2014 年普通高等学校招生全国统一考试(全国卷 2 卷) 数 学(理科) 一.选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要 求的. 1.设集合 M=｛0,1,2｝，N= ，则 =( ) A. ｛1｝ B. ｛2｝ C. ｛0，1｝ D. ｛1，2｝ 【答案】D 【解析】 把 M=｛0,1,2}中的数,代入不等式 经检验 x=1,2 满足。所以选 D. 2.设复数 ， 在复平面内的对应点关于虚轴对称， ，则 （ ） A. - 5 B. 5 C. - 4+ i D. - 4 - i 【答案】B 【解析】 3.设向量 a,b 满足|a+b|= ，|a-b|= ，则 a b = ( ) A. 1 B. 2 C. 3 D. 5 【答案】A 【解析】 4.钝角三角形 ABC 的面积是 ，AB=1，BC= ，则 AC=( ) A. 5 B. C. 2 D. 1 【答案】B 【解】 { }2| 3 2 0x x x− + ≤ M N∩ ,023-2 ≤+xx 1z 2z 1 2z i= + 1 2z z = .,5-4-1-∴ ,2-,2 21 2211 Bzz izzziz 故选 关于虚轴对称，与 == +=∴+= 10 6 ⋅ .,1 ,62-102∴,6|-|,10|| 2222 Aba babababababa 故选联立方程解得 ，， = =+=++==+ 1 2 2 5 5.某地区空气质量监测资料表明，一天的空气质量为优良的概率是 0.75，连续两为优良的概率是 0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率 是（ ） A. 0.8 B. 0.75 C. 0.6 D. 0.45 【答案】 A 【解析】 6.如图，网格纸上正方形小格的边长为 1（表示 1cm）,图中粗线画出的是某零件的三视图，该零件 由一个底面半径为 3cm，高为 6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的 比值为（ ） A. B. C. D. 【答案】 C 【解析】 7.执行右图程序框图，如果输入的 x,t 均为 2，则输出的 S= （ ） A. 4 B. 5 C. 6 D. 7 【答案】 C 【解析】 ..5,cos2-4 3π∴ ΔABC4 π.4 3π,4 π∴ ,2 2sin∴2 1sin122 1sin2 1 222 ΔABC BbBaccabB BB BBBacS 故选解得，使用余弦定理， 符合题意，舍去。为等腰直角三角形，不时，经计算当或 =+== == ==•••== .,8.0,75.06.0 , App p 故选解得则据题有 优良的概率为则随后一个空气质量也设某天空气质量优良， =•= 17 27 5 9 10 27 1 3 ..27 10 π54 π34-π54 π.342π944 .2342 π.546π963 2 1 C v v 故选积之比削掉部分的体积与原体 体积 ，高为径为，右半部为大圆柱，半，高为小圆柱，半径加工后的零件，左半部 体积，，高加工前的零件半径为 ==∴ =•+•=∴ =•=∴ π   8.设曲线 y=ax-ln(x+1)在点(0,0)处的切线方程为 y=2x，则 a= A. 0 B. 1 C. 2 D. 3 【答案】 D 【解析】 9.设 x,y 满足约束条件 ，则 的最大值为（ ） A. 10 B. 8 C. 3 D. 2 【答案】 B 【解析】 10.设 F 为抛物线 C: 的焦点，过 F 且倾斜角为 30°的直线交 C 于 A,B 两点，O 为坐标原点， 则△OAB 的面积为（ ） A. B. C. D. 【答案】 D 【解析】 . 372 252 131 ,2,2 C KSM tx 故选 变量变化情况如下：== ..3.2)0(,0)0( .1 1-)(),1ln(-)( Daff xaxfxaxxf 故选联立解得且 ==′=∴ +=′∴+= 7 0 3 1 0 3 5 0 x y x y x y + −  − +  − − ≤ ≤ ≥ 2z x y= − ..8 ,)2,5(07-013--2 Bz yxyxyxz 故选取得最大值 处的交点与在两条直线 可知目标函数三角形，经比较斜率，画出区域，可知区域为 = =+=+= 2 3y x= 3 3 4 9 3 8 63 32 9 4 11.直三棱柱 ABC-A1B1C1 中，∠BCA=90°，M，N 分别是 A1B1，A1C1 的中点，BC=CA=CC1， 则 BM 与 AN 所成的角的余弦值为（ ） A. B. C. D. 【答案】 C 【解析】 12.设函数 .若存在 的极值点 满足 ，则 m 的取值范 围是（ ） A. B. C. D. 【答案】 C 【解析】 ..4 9)(4 3 2 1 .6),3-2(2 3),32(2 33-4 322,34 322 2,2 ΔOAB DnmS nmnmnnmm nBFmAFBA 故选 ，解得 直角三角形知识可得，，则由抛物线的定义和，分别在第一和第四象限、设点 =+••=∴ =+∴=+=•=+•= == 1 10 2 5 30 10 2 2 ..10 30 56 41-0 |||| θcos 2-1-,0(2-1,1-(∴).0,1,0(),0,1,1(),2,0,2(),2,2,0( ,2,, 111111 C ANBM ANBM ANBMNMBA CCBCACZYXCCACBC 故选 ）。，），， 则轴，建立坐标系。令为，，如图，分别以 =+= • •= == === ( ) 3sin xf x m π= ( )f x 0x ( ) 22 2 0 0x f x m+ <   ( ) ( ), 6 6,−∞ − ∪ ∞ ( ) ( ), 4 4,−∞ − ∪ ∞ ( ) ( ), 2 2,−∞ − ∪ ∞ ( ) ( ), 1 4,−∞ − ∪ ∞ 第Ⅱ卷 本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题，每个试题考生必须做答.第 22 题 ~第 24 题为选考题，考生根据要求做答. 二.填空题 13. 的展开式中， 的系数为 15，则 a=________.(用数字填写答案) 【答案】 【解析】 14.函数 的最大值为_________. 【答案】 1 【解析】 15. 已 知 偶 函 数 在 单 调 递 减 ， . 若 ， 则 的 取 值 范 围 是 __________. 【答案】 【解析】 2 1 ），（）， ∞3∪1-∞-( + .2.||,34∴34)]([ ,2 ||||,3)]([3πsin3)( 2 22 2 0 2 0 0 2 0 Cmmmmxfx mxxfm xxf 故选解得， ，即的极值为 ><++≥+∴ ≤=±= ( )10x a+ 7x .2 1.2 1,15a∴15xax 33 10 7373 10 ==== aaCC 故 ( ) ( ) ( )sin 2 2sin cosf x x xϕ ϕ ϕ= + − + .1∴.1≤sin φsin)φcos(-φcos)φsin( )φcos(φsin2-φsin)φcos(φcos)φsin( )φcos(φsin2-)φ2sin()( 最大值为x xx xxx xxxf = •+•+= +•++•+= ++= ( )f x [ )0,+∞ ( )2 0f = ( )1 0f x − > x .∞3∪1-∞-(∈2|1-| .31--(2|1-|0)1-(∴ .2||0)(∴ 0)2(),0[)( ），（），，解得故解集为 ），（），，解得的解集为 的解集为 上单增，且在偶函数 +> +∞∪∞∈>> >> =+∞= xx xxxf xxf fxfy 16.设点 M（ ,1），若在圆 O: 上存在点 N，使得∠OMN=45°，则 的取值范围是 ________. 【答案】 【解析】 三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分 12 分） 已知数列 满足 =1， . （Ⅰ）证明 是等比数列，并求 的通项公式； （Ⅱ）证明： . 【答案】 (1) 无 （2） 无 【解析】 （1） (2) 18. （本小题满分 12 分） ]1,1-[ 0x 2 2 1x y+ = 0x ].1,1-[∈x].1,1-[x .,1)M(x1,yO 00 0 故形外角知识，可得由圆的切线相等及三角 在直线上其中和直线在坐标系中画出圆 ∈ = { }na 1a 1 3 1n na a+ = + { }1 2na + { }na 1 2 31 1 1 2na a a + + <… + 的等比数列。公比为是首项为 3,2 3 2 1}2 1{∴ ).2 1(32 1132 1a∴ .*N∈.n13,1 1 1n 11 =++ +=++=+ +== + + aa aa aaa n nn nn （证毕），所以， ）（ 时，当 ，知，由 .*∈2 31111 .2 3 3 1-12 3 3 1-1 3 1-1 3 1 3 1 3 111111∴ .3 1 1-3 211,11 .1-3 21 2 1-3∴,2 3 2 1)1( 321 1-21 321 1- 1 Nnaaaa aaaa ana aaa n n n n n nn n n n n n n n <++++ <==++++<++++ <=>= ===+   如图，四棱锥 P-ABCD 中，底面 ABCD 为矩形，PA⊥平面 ABCD，E 为 PD 的中点. （Ⅰ）证明：PB∥平面 AEC； （Ⅱ）设二面角 D-AE-C 为 60°，AP=1，AD= ，求三棱锥 E-ACD 的体积. 【答案】 (1) 无 （2） 无 【解析】 （1） 设 AC 的中点为 G, 连接 EG。在三角形 PBD 中，中位线 EG//PB,且 EG 在平面 AEC 上，所以 PB// 平面 AEC. （2）设 CD=m, 分别以 AD,AB,AP 为 X,Y,Z 轴建立坐标系，则 3 。的体积为所以，三棱锥 的高即为三棱锥 面且的中点，则为设 解得 解得一个 则法向量为同理设平面 解得一个 则法向量为设平面 8 3- .8 3 2 132 3 2 1 3 1 3 1∴.- ,⊥,2 1 2,// .2 3,2 1 33 3 |||| |||,cos|3 πcos ).3-,3-,( ,0,0),,,( ).0,1,0( ,0,0),,,( ).0,,3(),2 1,0,2 3(),0,0,3(∴ ).0,,3(),2 1,0,2 3(),0,0,3(),0,0,0( Δ- 22 22 22 22 2 222222 1 111111 ACDE EFSVACDE ACDEFEFPAEFPAADF m mmnn nnnn mmn AEnACnzyxnACE n AEnADnzyxnADE mACAEAD mCEDA ACDACDE =••••=••= == == ++ = • •=><= = === = === ===  19. （本小题满分 12 分） 某地区 2007 年至 2013 年农村居民家庭纯收入 y（单位：千元）的数据如下表： 年份 2007 2008 2009 2010 2011 2012 2013 年份代号 t 1 2 3 4 5 6 7 人均纯收入 y 2.9 3.3 3.6 4.4 4.8 5.2 5.9 （Ⅰ）求 y 关于 t 的线性回归方程； （Ⅱ）利用（Ⅰ）中的回归方程，分析 2007 年至 2013 年该地区农村居民家庭人均纯收入的变化情 况，并预测该地区 2015 年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为： ， 【答案】 (1) （2） 约 6800 元 【解析】 （1） 20. （本小题满分 12 分） 设 , 分别是椭圆 的左右焦点，M 是 C 上一点且 与 x 轴垂直，直线 .3.25.0 += ty ( )( ) ( ) 1 2 1 n i i i n i i t t y y b t t ∧ = = − − = − ∑ ∑ ˆˆa y bt= − .3.25.0 3.24*2 1-3.4- ,2 1 2*14 14 2*)149( 8.48.15.007.0214*3 , 3.47 9.52.58.44.46.33.39.2,47 721 += === ==++ ++++++= += =++++++==+++= tyty tbya b abty yt 的回归方程为关于所以， 代入公式，经计算得设回归方程为  百元左右。千年，该区人均纯收入约所以，预计到 千元）该区人均纯收入 年，增长，预计到年该区人均纯收入稳步年至 862015 (8.63.295.0 201520132007∴,02 1 =+•= >= y b 1F 2F ( )22 2 2 1 0yx a ba b + = > > 2MF 与 C 的另一个交点为 N. （Ⅰ）若直线 MN 的斜率为 ，求 C 的离心率； （Ⅱ）若直线 MN 在 y 轴上的截距为 2，且 ，求 a,b. 【答案】 (1) （2） 【解析】 （1） （2） 21. （本小题满分 12 分） 已知函数 = （Ⅰ）讨论 的单调性； （Ⅱ）设 ，当 时， ,求 的最大值； （Ⅲ）已知 ，估计 ln2 的近似值（精确到 0.001） 2 1 72,7 == ba 1MF 3 4 15MN F N= .2 1∴.2 1 02-32.,4 3 2 1∴4 3 2222 2 21 1 的离心率为解得 ，联立整理得：且由题知， Ce eecbaca b FF MF = =++==•= 72,7 .72,7. ,,1:4:)2 3-(, :.2 3-,, .4, .422 222 1111 11 2 2 == ==+= ==+=+= == =•= ba bacba a ceNFMFceaNFecaMF ccNM mMFmNF a bMF 所以， 联立解得 ，且 由焦半径公式可得两点横坐标分别为 可得由两直角三角形相似，由题可知设 ，即知，由三角形中位线知识可 ( )f x 2x xe e x−− − ( )f x ( ) ( ) ( )2 4g x f x bf x= − 0x > ( ) 0g x > b 1.4142 2 1.4143< < 【答案】 (1) （2） 2 【解析】 （1） （2） （3） 请考生在第 22、23、24 题中任选一题做答，如果多做，同按所做的第一题计分，做答时请写清题 号. 22.（本小题满分 10）选修 4—1：几何证明选讲 如图，P 是 O 外一点，PA 是切线，A 为切点，割线 PBC 与 O 相 交于点 B，C，PC=2PA，D 为 PC 的中点，AD 的延长线交 O 于点 E. 证明： （Ⅰ）BE=EC； （Ⅱ）AD DE=2 上单增在Rxf )( .)( .02-12≥2-12-)(∴∈2--)( -- 上单增在所以， ， Rxf eeeeeexfRxxeexf x x x xxxxx =•+=+=′= 2≥22≥ 0-0≥)-(-))((0≥)-(2-2-2 .0≥)(0,tt),(0,∈∃ x∴)-(2-2-2)( .0)0(,0mm),(0,∈x)2-(2-2-)( .0≥)2-(2-2- 0≥)2-(4-4-22 .0≥)(0,mm),(0,∈∃ x∴)2-(4-4-22)( .0)0(,0),2--(4-4--)( .0,0)2--(4-4--)(4-)2()( --- -----2-2 -2-2 -2-2 -2-2 -2-2 -2-2 -2-2 -2-2 的最大值为，所以，即即 ，且，即即 使， 则，同理，令 即 即 使， 则令 bbeeeebee eeeebeeeeeebee xmeebeexm meebeexm eebee eebee xheebeexh hxxeebxeexh xxeebxeexbfxfxg xxxxxx xxxxxxxxxxxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx =•>++ >+ >=′ =>++= ++ ++ ′>++=′ =>= >>== .2 22ln4 1-23 2.4 1-23 22ln2 3-242ln6 ),2ln2- 2 1-282ln2-2 1-2)2(ln8)2(ln )2(ln8)2ln2(,02ln),(8)2()2(.2 22ln .02ln-2 22ln2- 2 1-2)2(ln,0)2(ln,02ln <<>> >> >>=>< >==>>= 所以，即 解得（，即即 ，则令知，由解得 即则设 ff ffxxfxf ffx    ⋅ 2PB 【答案】 (1) 无 （2）无 【解析】 （1） （2） 23. （本小题满分 10）选修 4-4：坐标系与参数方程 在直角坐标系 xoy 中，以坐标原点为极点，x 轴为极轴建立极坐标系，半圆 C 的极坐标方程为 ， . （Ⅰ）求 C 的参数方程； （Ⅱ）设点 D 在 C 上，C 在 D 处的切线与直线 垂直，根据（Ⅰ）中你得到的参数方 程，确定 D 的坐标. 所以 D 点坐标为 或 。 EC.BEBE∠CE∠BE∠αBE,∠βαβ BE∠∠DEB∠PDA∠∠∠∠∠ .AE∠CE,∠EB∠, ,,2 ===+=+∴ +===+=+ ====∠ Δ=∴== ，所以，即即 则连接 为等腰三角形。， DBDD DPADBADPABBCEPAB BBDPABAB PADPDPADCPDPAPC   αβ 2 2 2PA PA-PAPB-PB)PA-(PADCBD ,,PADC,BDDEAD PBPBPBPB PCPBPCPB PADCPDPCPB =•=• •=••==•∴ ==•=•=• ）（  2cosρ θ= 0, 2 πθ  ∈   : 3 2l y x= + 3 1(1 , )2 2 − 3 1(1 , )2 2 + − 24. （本小题满分 10）选修 4-5：不等式选讲 设函数 = （Ⅰ）证明： 2； （Ⅱ）若 ，求 的取值范围. ( )f x 1 ( 0)x x a aa + + − > ( )f x ≥ ( )3 5f < a