- 2021-05-22 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京市中考数学一模分类28题新定义
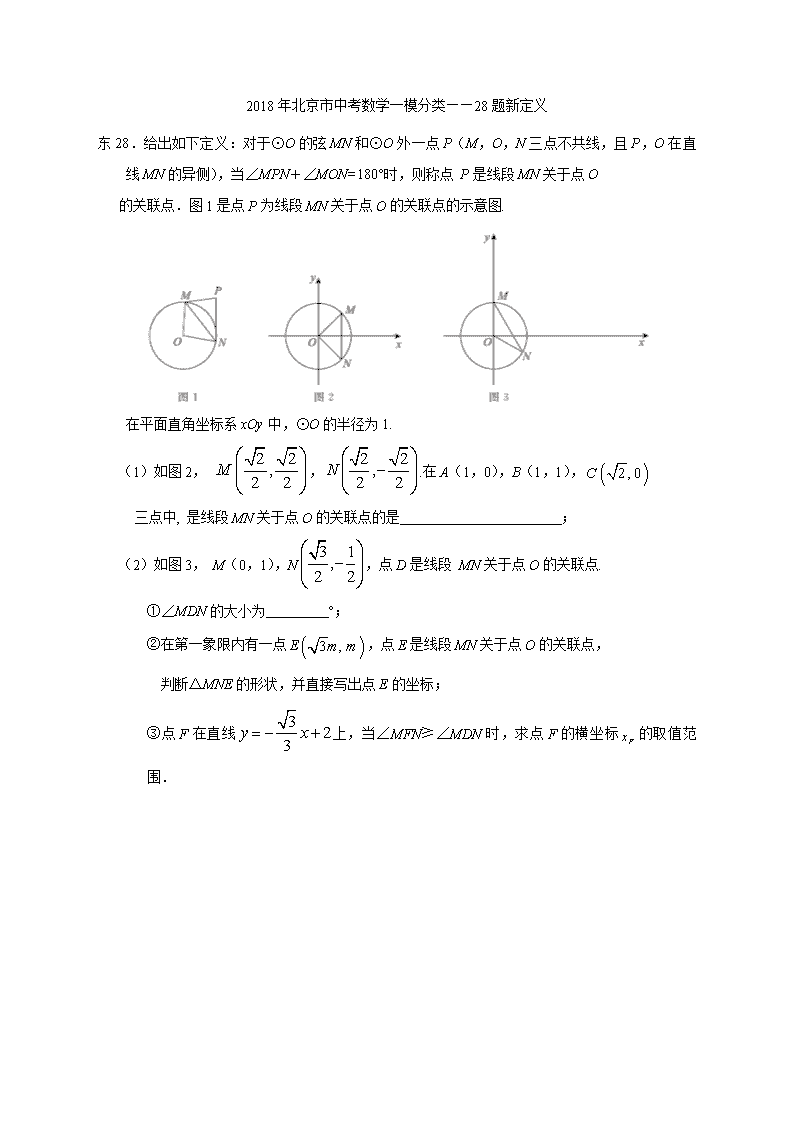
2018年北京市中考数学一模分类——28题新定义 东28.给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点 P是线段MN关于点O 的关联点.图1是点P为线段MN关于点O的关联点的示意图. 在平面直角坐标系xOy中,⊙O的半径为1. (1)如图2, ,.在A(1,0),B(1,1), 三点中, 是线段MN关于点O的关联点的是 ; (2)如图3, M(0,1),N,点D是线段 MN关于点O的关联点. ①∠MDN的大小为 °; ②在第一象限内有一点E,点E是线段MN关于点O的关联点, 判断△MNE的形状,并直接写出点E的坐标; ③点F在直线上,当∠MFN≥∠MDN时,求点F的横坐标的取值范围. 西28.对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设,则称点A(或点B)是⊙C的“k相关依附点”.特别地,当点A和点B重合时,规定AQ=BQ,(或). 已知在平面直角坐标系xOy中,,,⊙C的半径为r. (1)如图1,当时, ①若是⊙C的“k相关依附点”,则k的值为______; ②是否为⊙C的“2相关依附点”?答:是______(选“是”或“否”); (2)若⊙C上存在“k相关依附点”点M, ①当r =1,直线QM与⊙C相切时,求k的值; ②当k=时,求r的取值范围; (3)若存在r的值使得直线与⊙C有公共点,且公共点是⊙C的“相关依附点”,直接写出b的取值范围. 图1 备用图 海28.在平面直角坐标系中,对于点和,给出如下定义:若上存在一点不与重合,使点关于直线的对称点在上,则称为的反射点.下图为的反射点的示意图. (1)已知点的坐标为,的半径为, ①在点,,中,的反射点是____________; ②点在直线上,若为的反射点,求点的横坐标的取值范围; (2)的圆心在轴上,半径为,轴上存在点是的反射点,直接写出圆心的横坐标的取值范围. 朝28. 对于平面直角坐标系中的点P和线段AB,其中A(t,0)、B(t+2,0)两点,给出如下定义:若在线段AB上存在一点Q,使得P,Q两点间的距离小于或等于1,则称P为 线段AB的伴随点. (1)当t=3时, ①在点P1(1,1),P2(0,0),P3(-2,-1)中,线段AB的伴随点是 ; ②在直线y=2x+b上存在线段AB的伴随点M、N, 且MN,求b的取值范围; (2)线段AB的中点关于点(2,0)的对称点是C,将射线CO以点C为中心,顺时针 旋转30°得到射线l,若射线l上存在线段AB的伴随点,直接写出t的取值范围. 丰28.对于平面直角坐标系xOy中的点M和图形,给出如下定义:点P为图形上一点,点Q为图形上一点,当点M是线段PQ的中点时,称点M是图形,的“中立点”.如果点P(x1,y1),Q(x2,y2),那么“中立点”M的坐标为. 已知,点A(-3,0),B(0,4),C(4,0). (1)连接BC,在点D(,0),E(0,1),F(0,)中,可以成为点A和线段BC的“中立点”的是____________; (2)已知点G(3,0),⊙G的半径为2.如果直线y = - x + 1上存在点K可以成为点A和⊙G的“中立点”,求点K的坐标; (3)以点C为圆心,半径为2作圆.点N为直线y = 2x + 4上的一点,如果存在点N,使得轴上的一点可以成为点N与⊙C的“中立点”,直接写出点N的横坐标的取值范围. 石28.对于平面上两点A,B,给出如下定义:以点A或B为圆心, AB长为半径的圆称为点A,B的“确定圆”.如图为点A,B 的“确定圆”的示意图. (1)已知点A的坐标为,点的坐标为, 则点A,B的“确定圆”的面积为_________; (2)已知点A的坐标为,若直线上只存在一个点B,使得点A,B 的“确定圆”的面积为,求点B的坐标; (3)已知点A在以为圆心,以1为半径的圆上,点B在直线上, 若要使所有点A,B的“确定圆”的面积都不小于,直接写出的取值范围. 门28. 在平面直角坐标系xOy中,点M的坐标为,点N的坐标为,且,,我们规定:如果存在点P,使是以线段MN为直角边的等腰直角三角形,那么称点P为点M、N的 “和谐点”. (1)已知点A的坐标为, ①若点B的坐标为,在直线AB的上方,存在点A,B的“和谐点”C,直接写出点C的坐标; ②点C在直线x=5上,且点C为点A,B的“和谐点”,求直线AC的表达式. (2)⊙O的半径为,点D为点E、F的“和谐点”,若使得△DEF与⊙O有交点,画出示意图直接写出半径的取值范围. 备用图1 备用图2 顺28.如图1,对于平面内的点P和两条曲线、给出如下定义:若从点P任意引出一条射线分别与、交于、,总有是定值,我们称曲线与“曲似”,定值为“曲似比”,点P为“曲心”. 例如:如图2,以点O'为圆心,半径分别为、(都是常数)的两个同心圆、,从点O'任意引出一条射线分别与两圆交于点M、N,因为总有是定值,所以同心圆与曲似,曲似比为,“曲心”为O'. (1)在平面直角坐标系xOy中,直线与抛物线、分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由; (2)在(1)的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使⊙O与直线BC相切?若存在,求出k的值;若不存在,说明理由; (3)在(1)、(2)的条件下,若将“”改为“”,其他条件不变,当存在⊙O与直线BC相切时,直接写出m的取值范围及k与m之间的关系式. 通 怀28. P是⊙C外一点,若射线PC交⊙C于点A,B两点,则给出如下定义:若0<PAPB≤3,则点P为⊙C的“特征点”. (1)当⊙O的半径为1时. ①在点P1(,0)、P2(0,2)、P3(4,0)中,⊙O的“特征点”是 ; ②点P在直线y=x+b上,若点P为⊙O的“特征点”.求b的取值范围; (2)⊙C的圆心在x轴上,半径为1,直线y=x+1与x轴,y轴分别交于点M,N,若线段MN上的所有点都不是⊙C的“特征点”,直接写出点C的横坐标的取值范围. 房28. 在平面直角坐标系xOy中,当图形W上的点P的横坐标和纵坐标相等时,则称点P为图形W的“梦之点”. (1)已知⊙O的半径为1. ①在点E(1,1),F(,-),M(-2,-2)中,⊙O的“梦之点”为 ; ②若点P位于⊙O内部,且为双曲线(k≠0)的“梦之点”,求k的取值范围. (2)已知点C的坐标为(1,t),⊙C的半径为,若在⊙C上存在“梦之点”P,直接写出t的取值范围. (3)若二次函数的图象上存在两个“梦之点”,,且,求二次函数图象的顶点坐标. 大28.在平面直角坐标系中,过轴上一点作平行于轴的直线交某函数图象于点,点是轴上一动点,连接,过点作的垂线交轴于点(在线段上,不与点重合),则称为点,,的“平横纵直角”.图1为点,,的“平横纵直角”的示意图. 图1 如图2,在平面直角坐标系中,已知二次函数图象与轴交于点,与轴分别交于点(,0),(12,0). 若过点F作平行于轴的直线交抛物线于点. (1)点的横坐标为 ; 图2 (2)已知一直角为点的“平横纵直角”,若在线段上存在不同的两点、,使相应的点、都与点重合,试求的取值范围; (3)设抛物线的顶点为点,连接与交于点,当时,求的取值范围. 平28. 在平面直角坐标系xOy中,点M的坐标为,点N的坐标为,且,,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”. (1)已知点A(2,0),B(0,2),则以AB为边的“坐标菱形”的最小内角为_______; (2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式; (3)⊙O的半径为,点P的坐标为(3,m) .若在⊙O上存在一点Q ,使得以QP为边的“坐标菱形”为正方形,求m的取值范围. 延28.平面直角坐标系xOy中,点,与,,如果满足,,其中,则称点A与点B互为反等点. 已知:点C(3,4) (1)下列各点中, 与点C互为 反等点; D(3,4),E(3,4),F(3,4) (2)已知点G(5,4),连接线段CG,若在线段CG上存在两点P,Q互为反等点,求点P的横坐标的取值范围; (3)已知⊙O的半径为r,若⊙O与(2)中线段CG的两个交点互为反等点, 求r的取值范围.查看更多